ГЛАВА 12 Кластеризация по описательным признакам

В главе 5 мы рассмотрели способ извлечения многочисленных описательных признаков из временных рядов средствами пакета feasts. Такие признаки далее можно использовать для решения широкого круга задач, включая кластеризацию. В качестве примера воспользуемся данными из таблицы all_crypto_features (разд. 5.3), содержащей описательные признаки 22 временных рядов из набора данных cryptos (подразд. 1.5.1).

Для начала обратимся к базовой функции R heatmap(), которая строит диаграммы типа “тепловая карта”, а заодно выполняет и “двойную иерархическую кластеризацию” (biclustering) по входным данным. В результате такого анализа в группы объединяются как объекты (в нашем случае — временные ряды), так и описывающие их признаки. С одной стороны, двойная кластеризация помогает понять, сколько групп сходных объектов есть в исследуемых данных, а с другой — какие из признаков коррелируют друг с другом и, возможно, являются избыточными для описания соответствующих объектов. Подобный анализ можно выполнить с помощью базовой функции R heatmap():

x <- all_crypto_features %>% 
  dplyr::select(-c(coin, zero_var_cols(.))) %>%
  as.matrix()

heatmap(x, scale = "column",
        margins = c(10,10),
        col = hcl.colors(n = 12, palette = "viridis"),
        labRow = all_crypto_features$coin,
        cexCol = 0.9, cexRow = 0.9)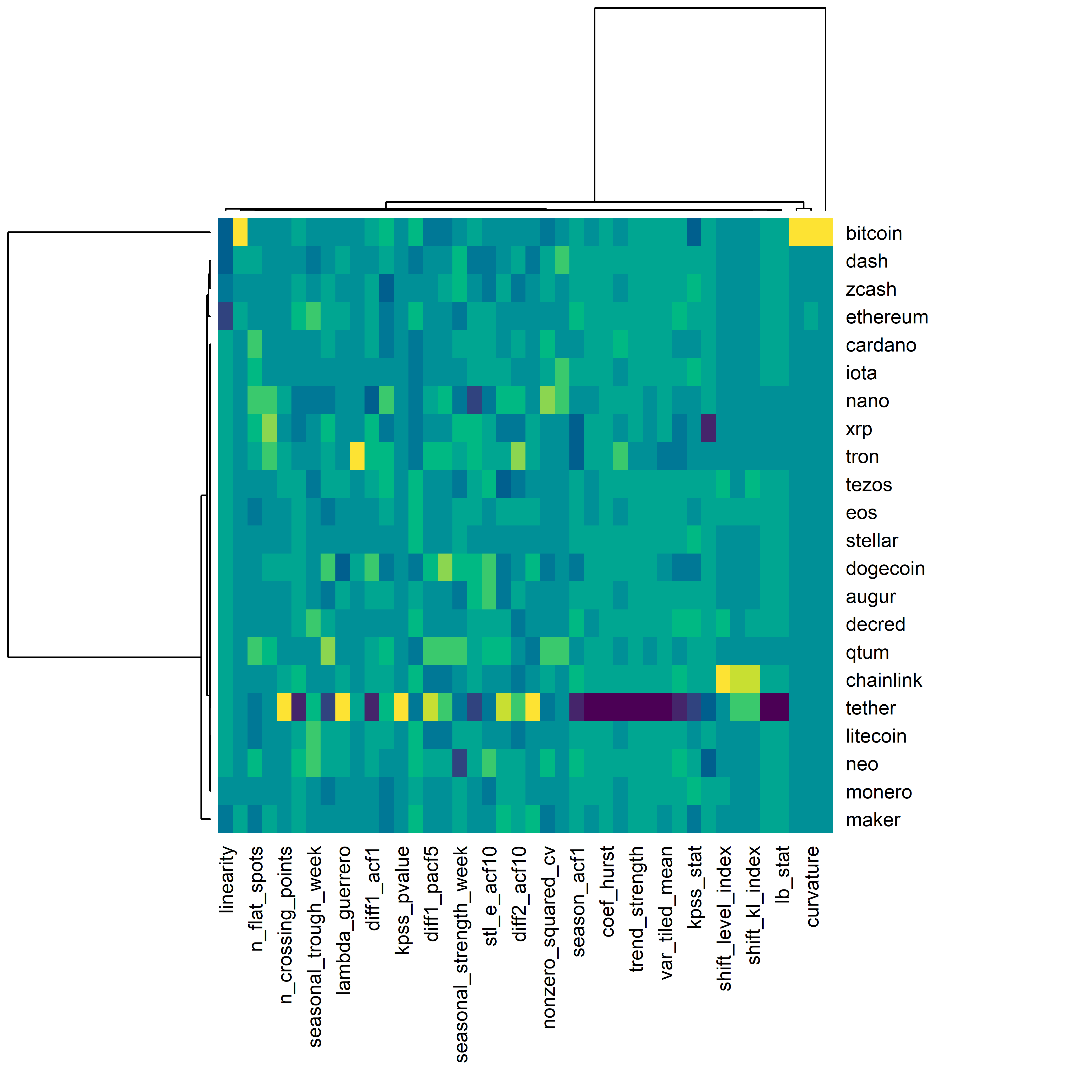

РИСУНОК 12.1: Результат выполнения двойного иерархического анализа по данным из таблицы all_crypto_features

На рис. 12.1 можно увидеть (хотя и с трудом, из–за размера диаграммы и свойств полученных дендрограмм), что по совокупности нескольких десятков признаков анализируемые криптовалюты образуют примерно 3–4 группы. Сами описательные признаки образуют примерно такое же количество группы, причем одна из групп включает подавляющее их большинство. Последнее обстоятельство указывает на наличие тесной корреляции между многими признаками. Это можно легко подтвердить также с помощью функции corrplot() из одноименного пакета, которая визуализирует корреляционные матрицы:

require(corrplot)

corrs <- cor(x, method = "spearman")
corrplot(corrs, type = "upper", order = "hclust", 
         tl.col = "black", tl.cex = 0.5, tl.srt = 45)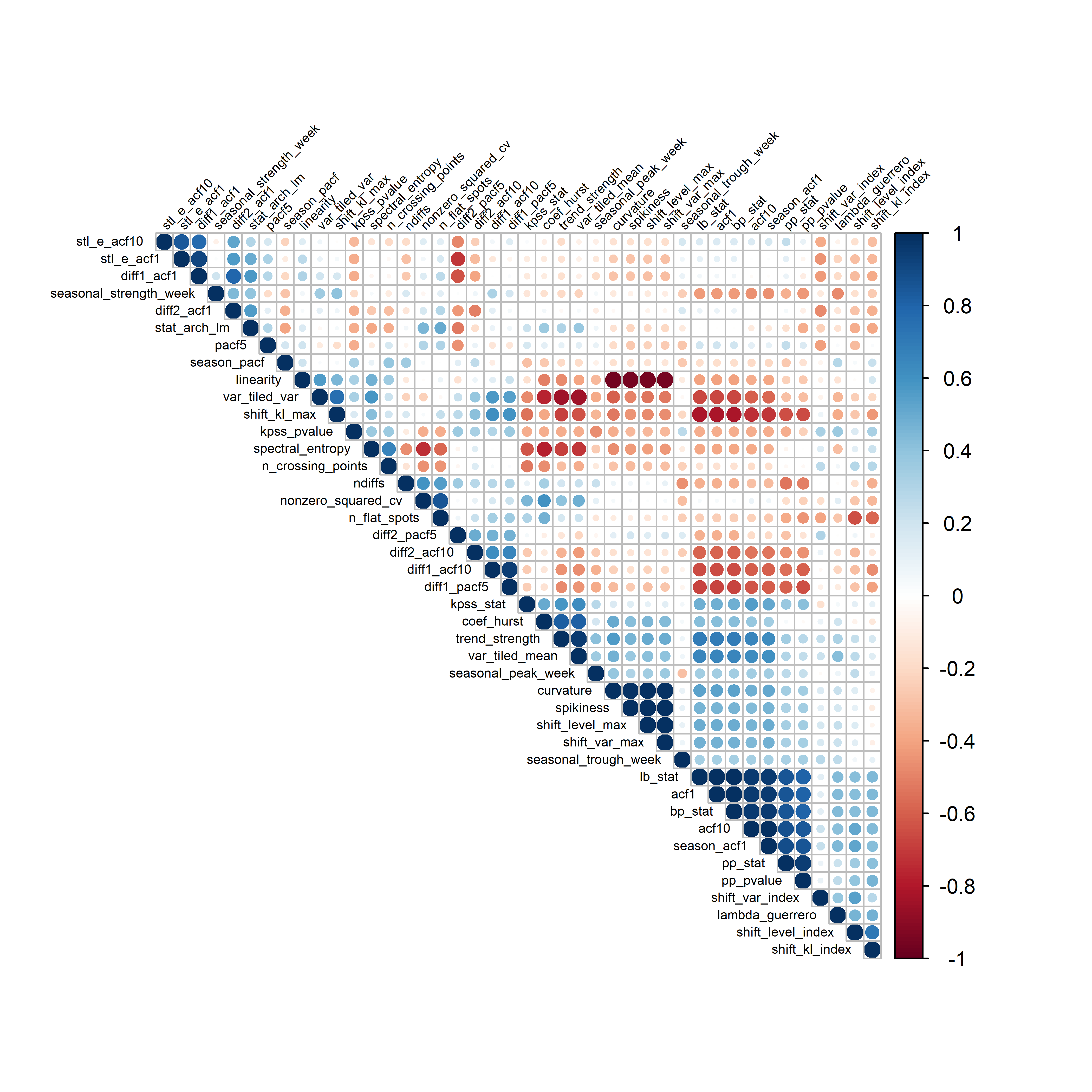

РИСУНОК 12.2: Корреляции между описательными признаками временных рядов из таблицы cryptos

На рис. 12.2 хорошо видно наличие нескольких выраженных групп тесно коррелирующих признаков. Это является проблемой для большинства методов кластерного анализа в силу “проклятия размерности”. Решить эту проблему позволяют методы снижения размерности данных, такие как метод главных компонент (PCA). В разд. 5.3 мы уже применили PCA к описательным признакам временных рядов из таблицы cryptos и обнаружили, что первые 10 главных компонент объясняют около 95% всей дисперсии в данных. Используем их для выполнения кластерного анализа по методу \(k\) средних с \(k = 4\):

pc <- all_crypto_features %>% 
  dplyr::select(coin) %>% 
  bind_cols(., as_tibble(pca$x))

set.seed(42)
cl <- pc %>% 
  dplyr::select(PC1:PC10) %>%
  kmeans(., centers = 4, nstart = 30)

Изобразим теперь исходные временные ряды, сгруппировав их в соответствии с результатами кластерного анализа:

require(ggrepel)

pc %>% 
  mutate(cluster = paste0("C", cl$cluster)) %>% 
  dplyr::select(coin, cluster) %>% 
  inner_join(., cryptos, by = "coin") %>%
  mutate(label = ifelse(ds == max(ds), coin, NA)) %>% 
  ggplot(., aes(ds, y, group = coin)) +
  geom_line() +
  geom_text_repel(aes(label = label),
                  size = 3, nudge_x = 50,
                  segment.size = 0.4,
                  segment.color = "gray60",
                  point.padding = 0.2,
                  force = 5, na.rm = TRUE) +
  scale_y_log10() +
  facet_wrap(~cluster, scales = "free_y") +
  theme_minimal() +
  xlim(c(as.Date("2018-01-01"), as.Date("2020-08-01")))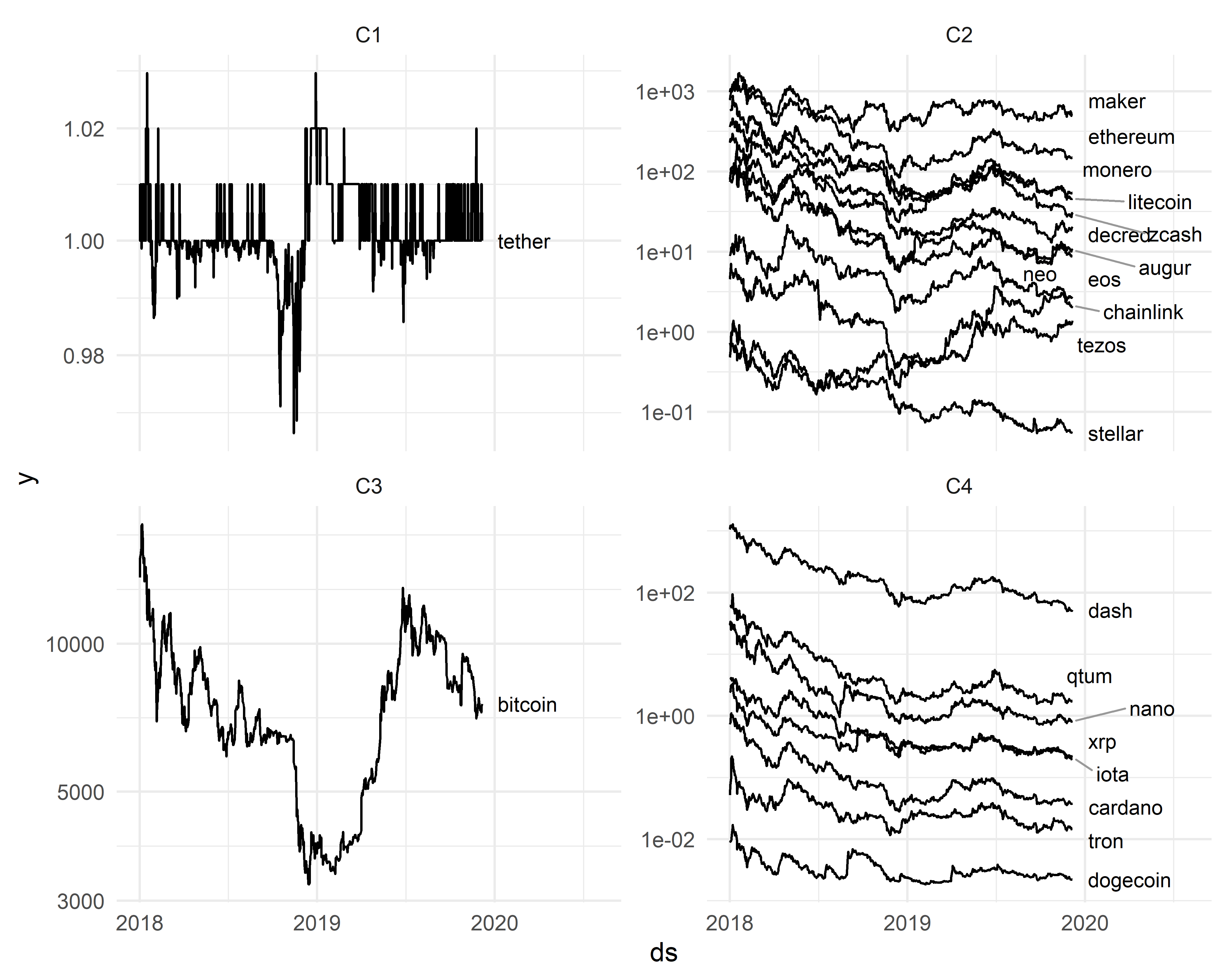

РИСУНОК 12.3: Результат применения кластеризации временных рядов из таблицы cryptos по методу \(k\) средних