ГЛАВА 4 Визуализация временных рядов и их свойств
Анализ временных рядов, равно как и данных других типов, практически невозможно представить себе без их визуализации в том или ином виде и многочисленные примеры графического представления временных рядов (преимущественно средствами пакета ggplot2) можно встретить на протяжении всей книги. В этой небольшой главе показаны некоторые дополнительные приемы, которые могут оказаться полезными в ходе разведочного анализа и подготовки данных к моделированию. Поскольку эти приемы являются стандартными, то их готовые реализации можно найти в нескольких пакетах для R. Мы воспользуемся одним из таких пакетов — feasts (от “feature extraction and statistics for time series”), который представляет собой коллекцию функций для визуализации временных рядов и расчета многочисленных показателей, обобщающих их свойства (гл. 5). Пакет feasts разработан в соответствии с принципами организации и анализа “опрятных данных”, что помимо простого и удобного синтаксиса команд делает его масштабируемым для одновременной обработки большого количества временных рядов, хранящихся в таблицах формата tsibble (разд. 1.4).
В примерах будем использовать данные по стоимости гостиничных номеров из таблицы hotels, которые мы сначала агрегируем (гл. 3) до среднедневных значений (на логарифмической шкале), а затем восстановим пропущенные наблюдения (гл. 2) путем простой линейной интерполяции (c помощью функции na.interp() из пакета forecast):
require(tsibble)
require(dplyr)
hotels_daily <- hotels %>%
group_by_key() %>%
index_by(dt = as.Date(date_time)) %>%
summarise(y = mean(log(price_usd))) %>%
fill_gaps() %>%
mutate(y = forecast::na.interp(y))Полученные временные ряды можно легко представить на графике с помощью функции autoplot() из пакета feasts, которая автоматически распознает наличие группирующей переменной в данных (prop_id) и изобразит три отдельные линии для каждой гостиницы:
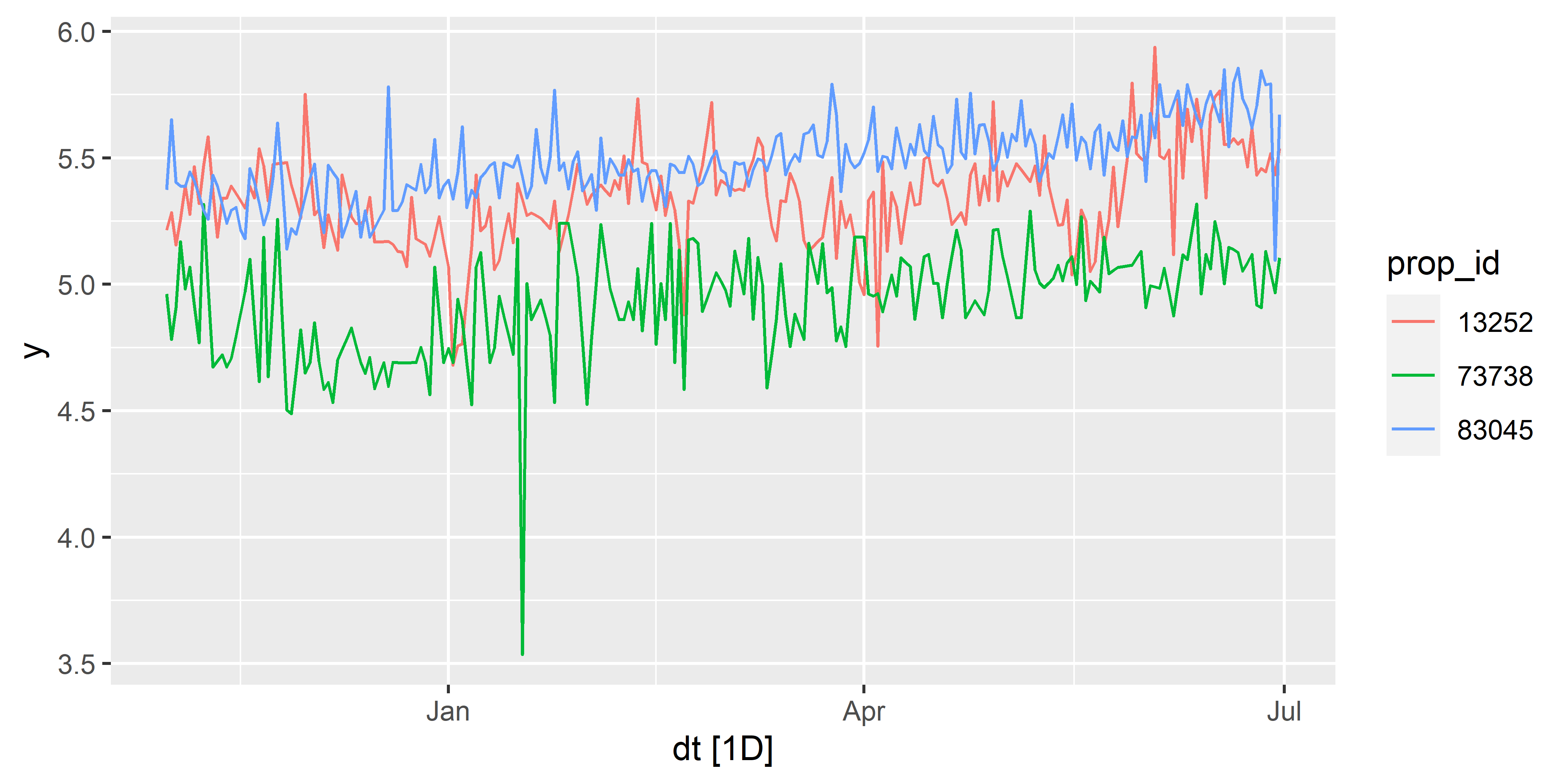
РИСУНОК 4.1: Результат применения функции feasts::autoplot() к таблице hotels_daily, которая является объектом класса tsibble с одной группирующей переменной (prop_id)
Функция autoplot() очень удобна для быстрого разведочного анализа данных: для построения графика на рис. 4.1 потребовалась всего одна строка кода. По внешнему виду полученного графика можно легко догадаться, что он представляет собой результат работы пакета ggplot2. Функция autoplot(), а также другие функции из пакета feasts, выполняющие визуализацию данных — это всего лишь “обертки” (wrappers), которые автоматически вызывают необходимые функции ggplot2 в соответствии с классом и структурой подаваемых на них объектов. Из этого, в частности, следует, что графические функции из пакета feasts можно использовать в сочетании со многими функциями ggplot2 для тонкой настройки внешнего вида графиков. Ниже мы воспользуемся этим обстоятельством и будем применять графические функции feasts в сочетании с theme_minimal() для изменения шаблона графиков со стандартного “серого” на предпочитаемый в этой книге “минимальный”.
Как было отмечено в разд. 1.3, многие (но далеко не все!) временные ряды в общем виде можно представить как сумму трех компонент: тренда, сезонных изменений и шума (колебаний, связанных со случайными факторами). Хорошее понимание структуры временного ряда является важным условием для построения надежных прогнозных моделей. К счастью, наше зрение устроено так, что часто мы без труда можем выделить тренд и сезонные изменения, просто глядя на график временного ряда. Однако при наличии слабого тренда и большого “шума” в данных, сделать это бывает труднее. В таких случаях может помочь декомпозиция временного ряда (time series decomposition) — прием, позволяющий автоматически разложить временной ряд на отдельные компоненты, которые далее можно изобразить графически.
Существует несколько методов декомпозиции временных рядов. Одним из наиболее широко используемых является разложение на тренд и сезонную составляющую с помощью локальной полиномиальной регрессии (Seasonal and Trend decomposition using Loess, STL; Cleveland et al. (1990)). Проще всего с этим методом можно разобраться, применив его к конкретным данным. Для примера воспользуемся данными по гостинице 73738 из созданной нами ранее таблицы hotels_daily (рис. 4.2):
hotels_daily %>%
filter(prop_id == 73738) %>%
model(STL(y ~ trend(window = 30) + season(period = "week"))) %>%
components() %>%
autoplot() + theme_minimal()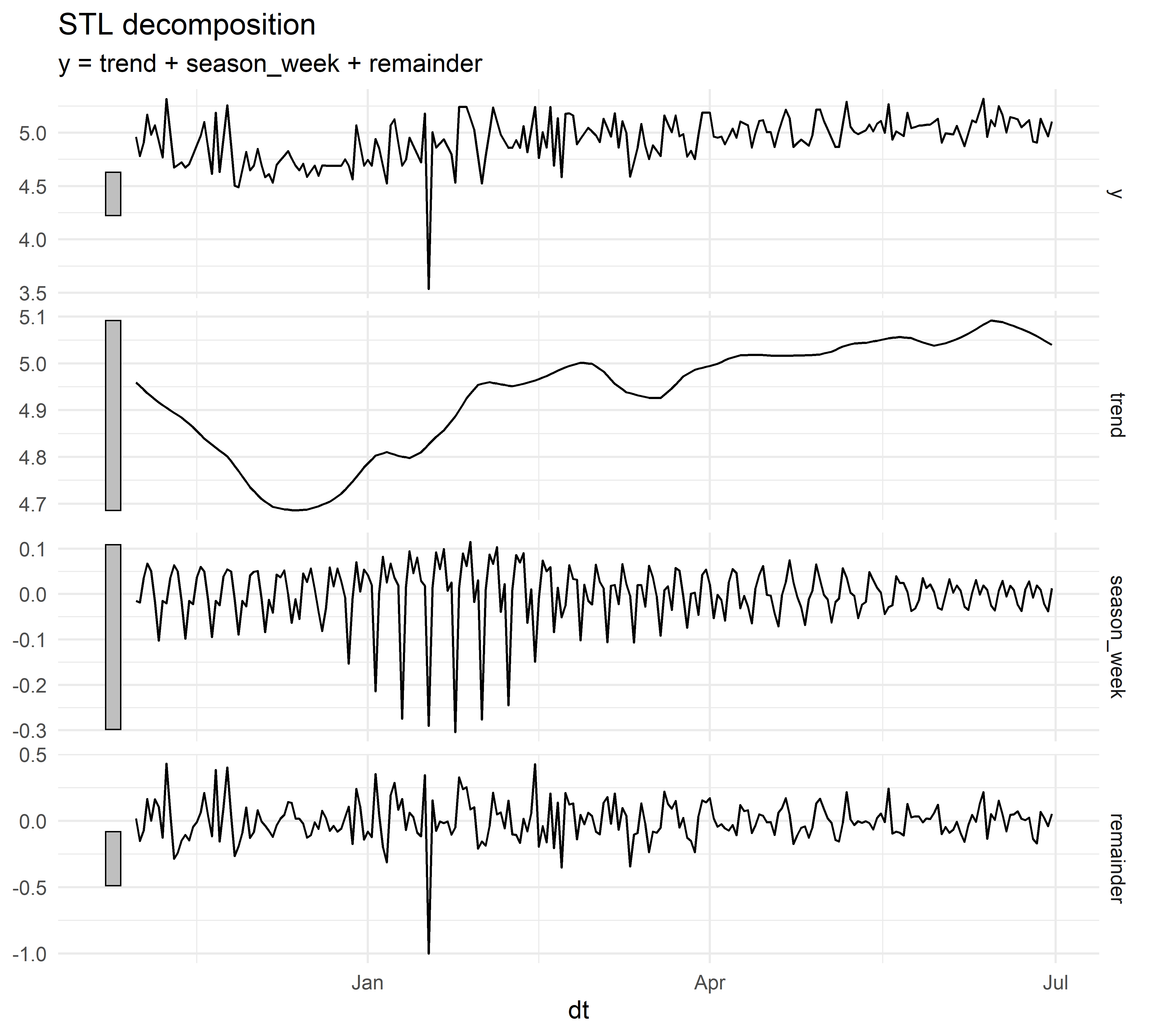
РИСУНОК 4.2: Результат применения метода STL для декомпозиции одного из временных рядов из таблицы hotels_daily
В приведенном коде использованы не встречавшиеся нам ранее функции из нескольких пакетов: model() и components() из пакета fabletools, который устанавливается и автоматически загружается одновременно с feasts, и STL() из пакета feasts. Для спецификации формулы STL–модели использованы также особые функции trend() и season() (подробнее см. справочный файл, доступный по команде ?STL). Аргумент window функции trend() задает количество наблюдений в скользящем окне, используемом для оценивания тренда (в данном случае 30; чем выше это число, тем более гладкой окажется в итоге кривая тренда). Аргумент period функции season() используется для указания периода сезонных колебаний (в данном случае одна неделя).
На рис. 4.2 выделенные с помощью метода STL компоненты временного ряда показаны на трех нижних графиках (trend — тренд, season_week — компонента недельной сезонности, remainder — остатки). Если их просуммировать, то получим исходный ряд y (приведен на верхнем графике). Серые вертикальные столбцы, изображенные слева от графиков, отражают удельный вклад каждой компоненты в общую дисперсию в данных. Чтобы лучше понять, что это значит, примем длину столбца на графике с исходными данными за единицу дисперсии. Длина столбца на графике тренда примерно в четыре раза больше, что указывает на незначительный вклад тренда в общую дисперсию. Другими словами, если бы мы сжали шкалу тренда настолько, чтобы длина его столбца стала равной длине столбца исходных данных, то дисперсия значений тренда оказалась бы довольно низкой. Аналогичный вывод можно сделать и в отношении вклада сезонной компоненты (который, что интересно, заметно варьирует во времени). В то же время длина столбца на графике остатков сравнима с длиной столбца на графике с исходными данными, что указывает на значительный вклад случайных факторов в общую дисперсию.
На рис. 4.2 приведен результат декомпозиции одного временного ряда, однако мы могли бы выполнить такую декомпозицию сразу для всех рядов, хранящихся в таблице hotels_daily (рис. 4.3):
hotels_daily %>%
group_by_key() %>%
model(STL(y ~ trend(window = 30) + season(period = "week"))) %>%
components() %>%
autoplot() + theme_minimal() +
theme(legend.position = "bottom", legend.direction = "vertical")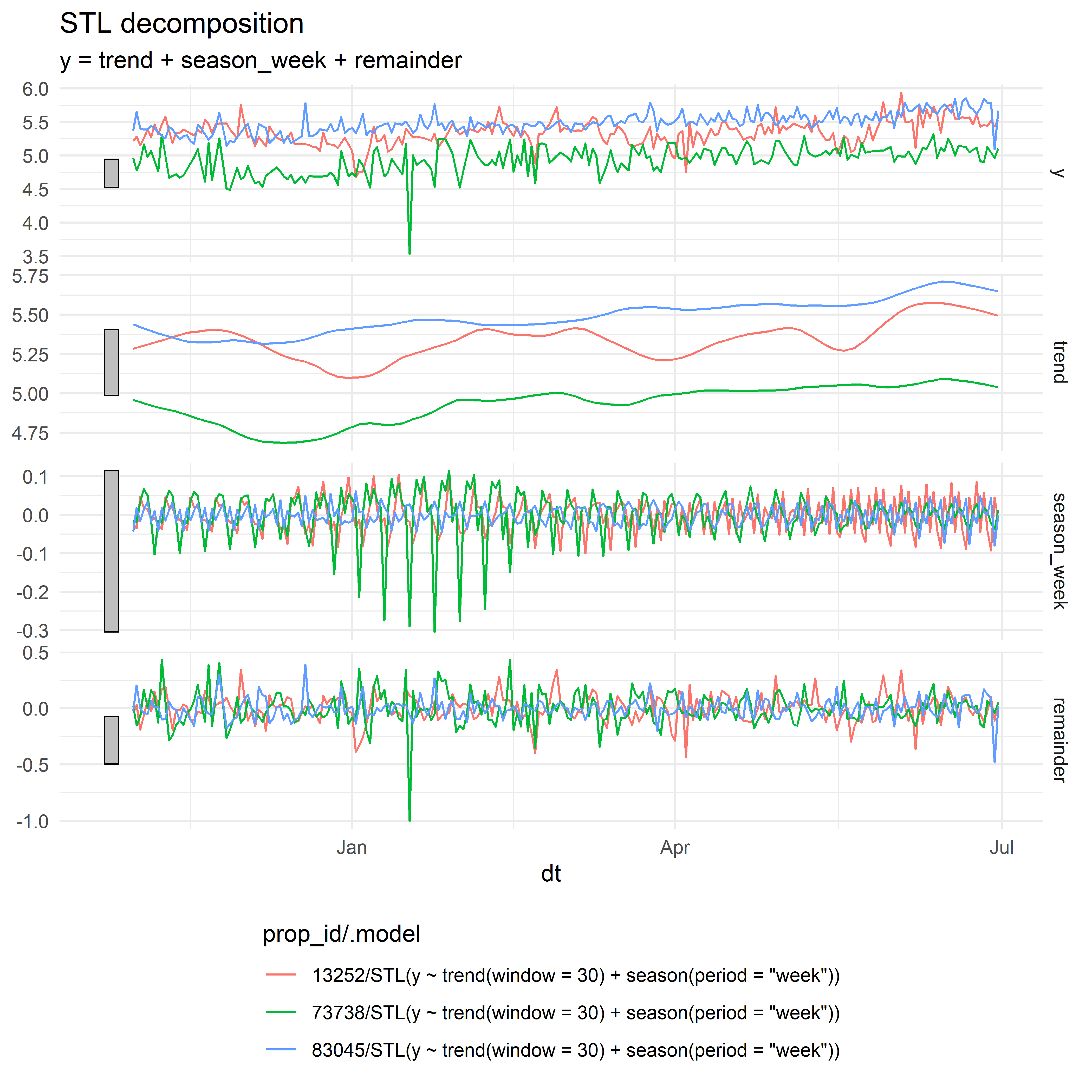
РИСУНОК 4.3: Результат применения метода STL для декомпозиции всех трех временных рядов из таблицы hotels_daily
Более детальное изучение сезонных колебаний в анализируемых временных рядах можно выполнить также с помощью функции gg_season() из пакета feasts(). В приведенном ниже примере эта функция применена для изображения динамики среднедневных значений стоимости номеров в каждой гостинице в течение каждой недели исследованного периода времени. На рис. 4.4 хорошо видно отсутствие каких–либо выраженных колебаний стоимости гостиничных номеров в течение недели, что согласуется с полученными ранее результатами декомпозиции этих временных рядов:
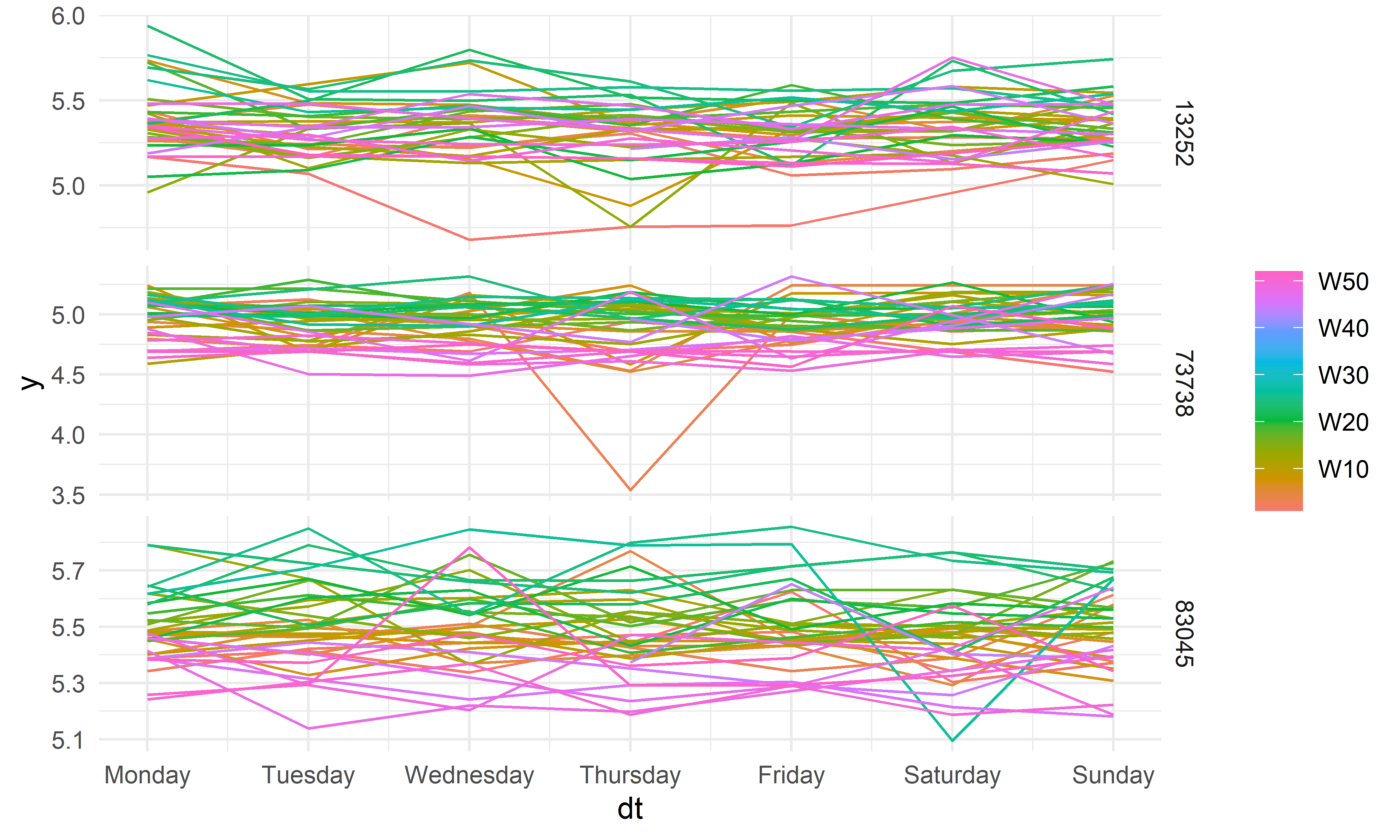
РИСУНОК 4.4: Динамика среднедневной стоимости номеров в гостиницах из таблицы hotels_daily в течение каждой недели исследованного периода времени
Важным свойством многих временных рядов является наличие автокорреляции в их значениях, т.е. связи между значениями одного ряда, взятыми с определенным сдвигом (“лагом”, или “задержкой”). Наличие автокорреляции в данных является важной информацией для построения надежных прогнозных моделей. Выявление автокорреляции в остатках таких моделей также важно для диагностики их качества (в надежных моделях такой корреляции в остатках быть не должно).
Визуально корреляцию между значениями одного временного ряда на разных сдвигах (по умолчанию от 1 до 9) можно представить с помощью функции gg_lag() из пакета feasts():
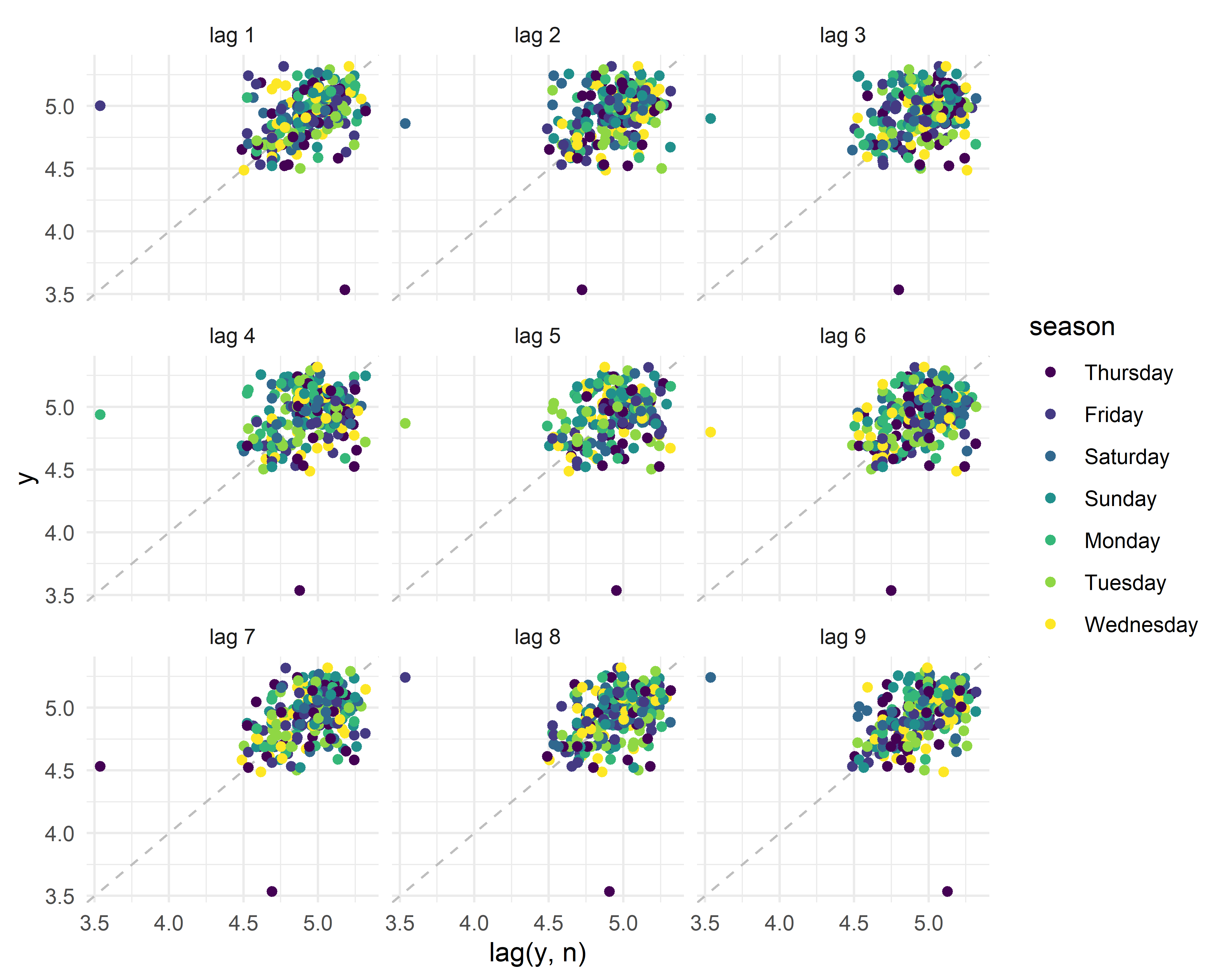
РИСУНОК 4.5: Связь между значениями временного ряда 73738 из таблицы hotels_daily и его копиями, сдвинутыми на несколько временных отметок (от 1 до 9)
На рис. 4.5 видна умеренная связь между значениями временного ряда гостиницы 73738 на всех девяти сдвигах. Существует несколько способов, позволяющих выразить степень связи между временным рядом и его сдвинутыми копиями (т.е. автокорреляционную функцию) количественно. В простейшем случае для этого рассчитывают обычный линейный коэффициент корреляции: \[r_k = \frac{\sum_{t=k+1}^T (y_t - \bar{y})(y_{t-k} - \bar{y})}{\sum_{t=1}^T (y_t - \bar{y})^2},\] где \(T\) — это длина временного ряда. В пакете feasts для расчета автокорреляционной функции служит команда ACF(). По умолчанию ACF() выполняет вычисления для сдвигов от 1 до 23, однако максимальный сдвиг можно изменить с помощью аргумента lag_max:
## # A tsibble: 6 x 3 [1D]
## # Key: prop_id [1]
## prop_id lag acf
## <dbl> <lag> <dbl>
## 1 73738 1D 0.350
## 2 73738 2D 0.315
## 3 73738 3D 0.234
## 4 73738 4D 0.242
## 5 73738 5D 0.265
## 6 73738 6D 0.315Полученные коэффициенты корреляции принято изображать в виде графика, который называют коррелограммой; рис. 4.6):
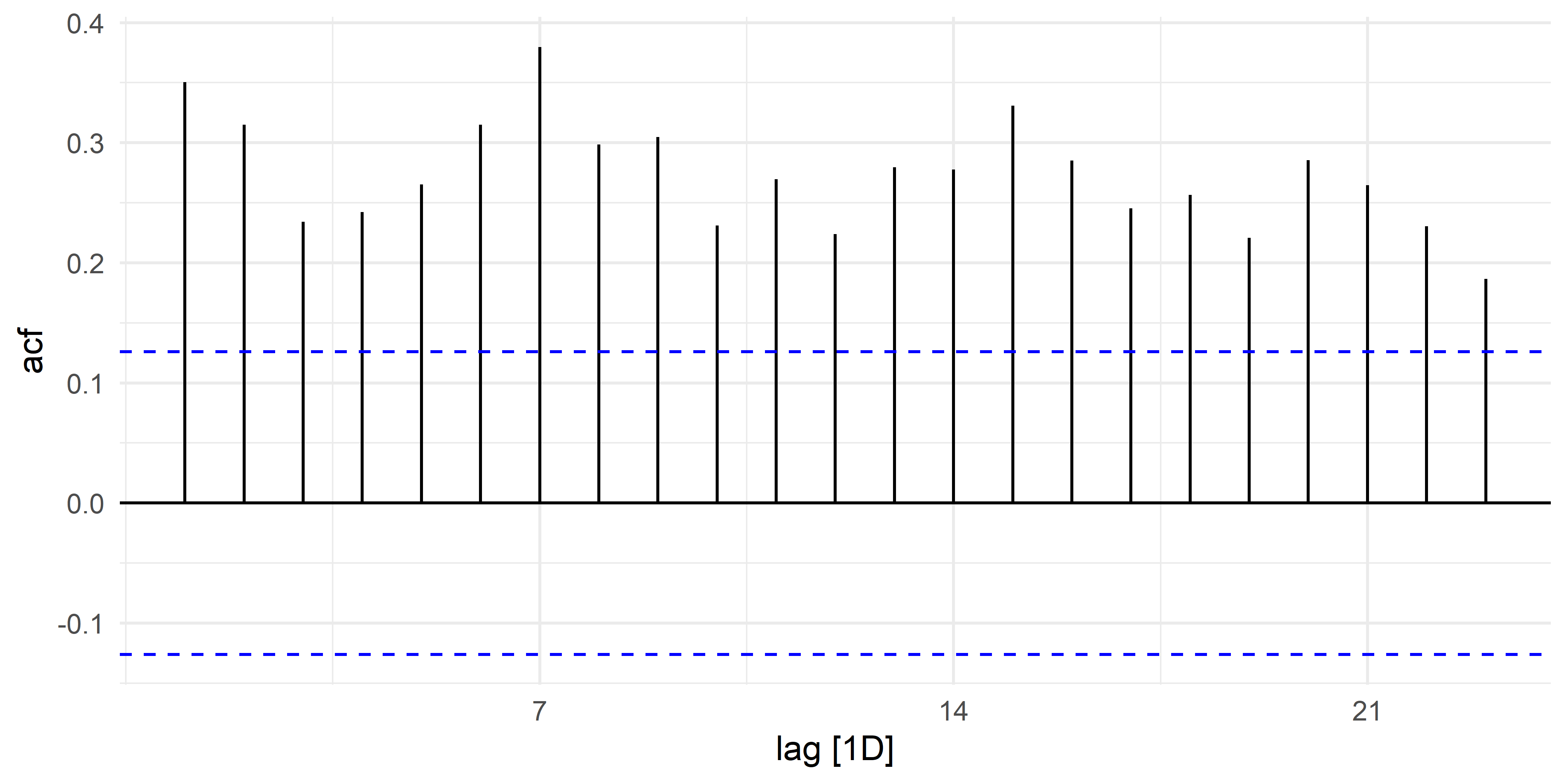
РИСУНОК 4.6: Коррелограмма временного ряда 73738 из таблицы hotels_daily для сдвигов от 1 до 23
На полученном графике видно, что все коэффициенты автокорреляции являются умеренно положительными, указывая на наличие во временном ряду тренда на возрастание. Кроме того, можно видеть небольшие “всплески” коэффициентов, видимо обусловленные (слабо выраженной) недельной сезонностью. Синие пунктирные линии соответствуют критическим значениям корреляции (на уровне значимости 0.05). Если полученные коэффициенты по модулю превышают эти критические значения (как в нашем случае), то соответствующие корреляции можно считать значимо отличающимися от нуля.
На этом мы завершим рассмотрение способов графического представления временных рядов и их свойств. С некоторыми дополнительными приемами визуализации можно познакомиться в великолепной книге Hyndman and Athanasopoulos (2019).