ГЛАВА 8 Выявление структурных изменений

Практически любая промышленная система сегодня снабжена совокупностью сенсоров, датчиков и других измерительных устройств, позволяющих вести учет ее состояния (часто в реальном времени). Количество таких измерительных устройств и учитываемых с их помощью показателей может быть очень большим, что требует автоматизации процесса мониторинга и своевременного оповещения о нестандартных (например, предаварийных и аварийных) ситуациях. Подобные нестандартные ситуации обычно сопряжены с существенными изменениям во временных рядах, описывающих те или иные показатели. Одним из типов таких изменений является сдвиг среднего уровня временного ряда, который может быть как очень резким, так и постепенным (рис. 8.1). Существует несколько методов, позволяющих автоматически обнаруживать подобные структурные изменения во временных рядах. Одним из них является метод “E–Divisive with Medians” (EDM), разработанный исследователями из Корнеллского университета и компании Twitter (James, Kejariwal, and Matteson 2015) и реализованный в пакете для R BreakoutDetection. В этой главе приведено краткое описание основ работы с данным пакетом.

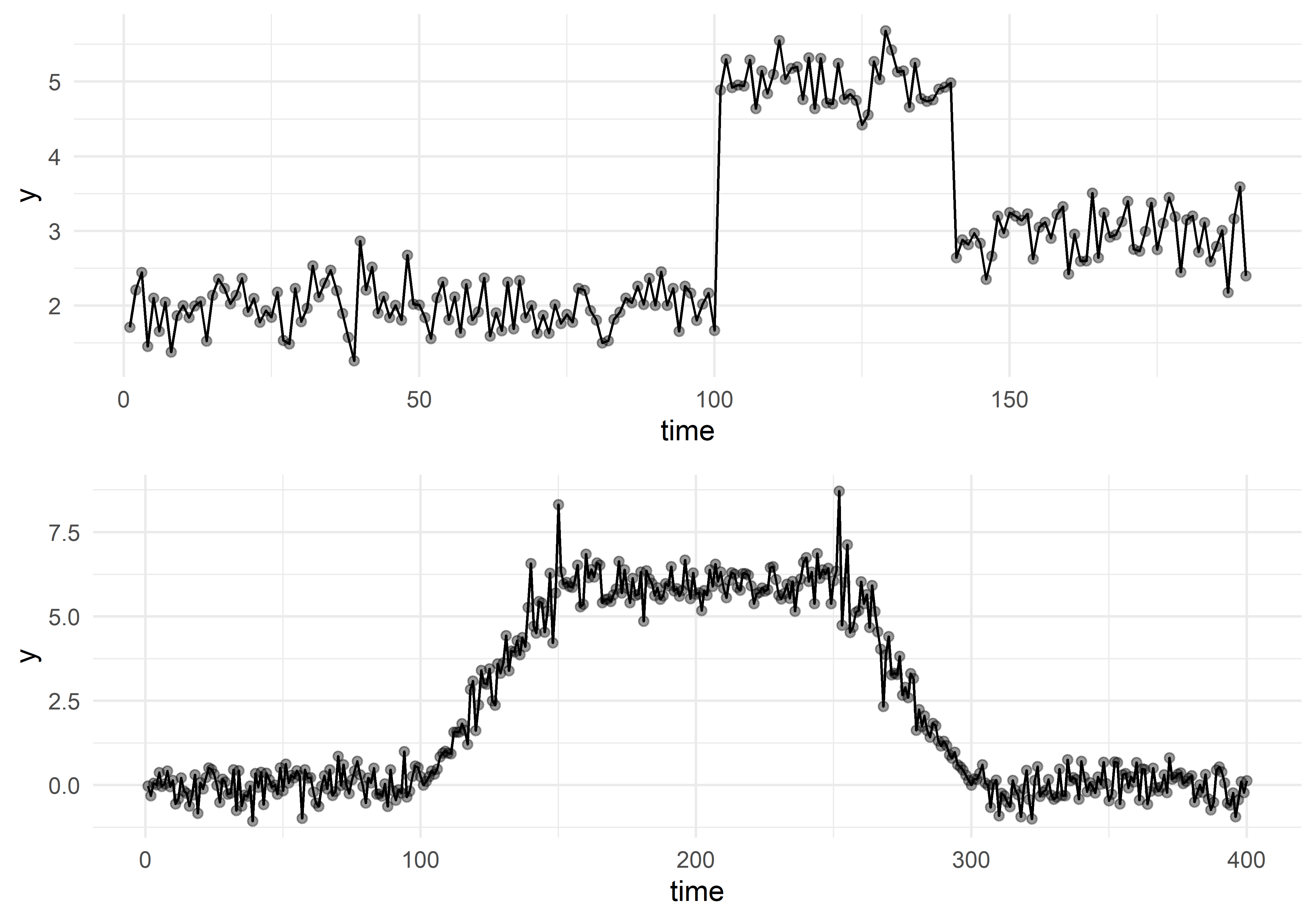
Примеры структурных изменений во временных рядах: резкое (вверху) и плавное (внизу)

РИСУНОК 8.1: Примеры структурных изменений во временных рядах: резкое (вверху) и плавное (внизу)

Пакет BreakoutDetection можно установить только из репозитория GitHub, для чего достаточно воспользоваться функцией install_github() из пакета devtools (который, конечно, тоже нужно сначала установить, если у вас его еще нет):

8.1 Метод “E–Divisive with Medians” (EDM)

Подробное описание теории, лежащей в основе EDM, приведено в статье James, Kejariwal, and Matteson (2015). Вкратце, этот метод основан на использовании т.н. \(E\)–статистики (от “energy”, т.е. “энергия”), которая характеризует расстояние между наблюдениями из случайных выборок. Чем больше эта статистика, тем больше оснований считать, что сравниваемые выборки происходят из разных генеральных совокупностей. Во избежание влияния обычных на практике аномальных наблюдений, метод EDM оперирует не средними значениями, а медианами. Более того, это непараметрический метод, т.е. он не исходит из предположения о принадлежности анализируемых наблюдений к каким–либо конкретным распределениям вероятностей. Непараметрическая природа EDM, а также использование медианы в качестве меры центральной тенденции, делают этот метод особенно подходящим для обнаружения структурных изменений во временных рядах при решении практических задач.

8.2 Функция breakout()

В пакете BreakoutDetection есть всего лишь одна функция — breakout(), которая имеет следующие аргументы:

  • Z — временной ряд, который может быть представлен либо в виде числового вектора, либо в виде таблицы данных со столбцами timestamp (“временная отметка”) и count (“количество”).
  • min.size — минимальное количество наблюдений, которое должно иметь место между точками излома тренда во временном ряду (по умолчанию равно 30).
  • method — название применяемого к данным сценария по обнаружению структурных изменений. Принимает два возможных значения: "amoc" (от “at most one change”, т.е. “не более одного изменения”) и "multi" (несколько точек излома).
  • ... — дополнительные аргументы.

Набор дополнительных аргументов (...) зависит от значения параметра method. В обоих случаях (т.е. и "amoc", и "multi") функция примет следующие аргументы:

  • plot — логический значение, включающее (TRUE) или отключающее (FALSE) построение графика временного ряда с отметками позиций обнаруженных точек излома тренда;
  • xlab и ylab — подписи осей графика;
  • title — заголовок графика.

Если method = "amoc", то функция breakout() примет также:

  • alpha — параметр, используемый в EDM для придания разных весов расстояниям между наблюдениями. Принимает любое значение из интервала (0, 2] (по умолчанию alpha = 2).
  • exact — логический аргумент. По умолчанию равен TRUE, что приводит к расчету точных значений медиан при нахождении точек излома (в случае с длинными рядами это может сопровождаться длительными вычислениями).
  • sig.lvl — желаемый уровень статистической значимости теста для обнаруженной точки излома тренда (по умолчанию равен 0.05).
  • nperm — количество итераций при выполнении перестановочного теста. По умолчанию nperm = 0, т.е. перестановочный тест не выполняется.

Когда требуется обнаружить несколько точек излома тренда (method = "multi"), на функцию breakout() можно подать также следующие аргументы, задающие уровень регуляризации в отношении количества и близости взаимного расположения этих точек:

  • degree — параметр, определяющий близость расположения точек излома. Принимает значения 0, 1 (принято по умолчанию) и 2. Чем больше этот параметр, тем меньше точек излома располагаются близко друг к другу.
  • percent — задает минимальное относительное (%) увеличение внутреннего критерия качества EDM (здесь не рассматривается), необходимое для классификации того или иного наблюдения как точки излома тренда. Например, значение 0.25 соответствует 25%–ному увеличению критерия. Аргумент percent не имеет значения, принятого по умолчанию.
  • beta — принимает любое числовое значение (по умолчанию равен 0.008) и используется для регуляризации если degree и/или percent не заданы. Чем больше этот параметр, тем меньше точек излома будет обнаружено алгоритмом.

8.3 Примеры использования функции breakout()

Применим функцию breakout() с ее принятыми по умолчанию параметрами к данным по стоимости биткоина (подразд. 1.5.2):

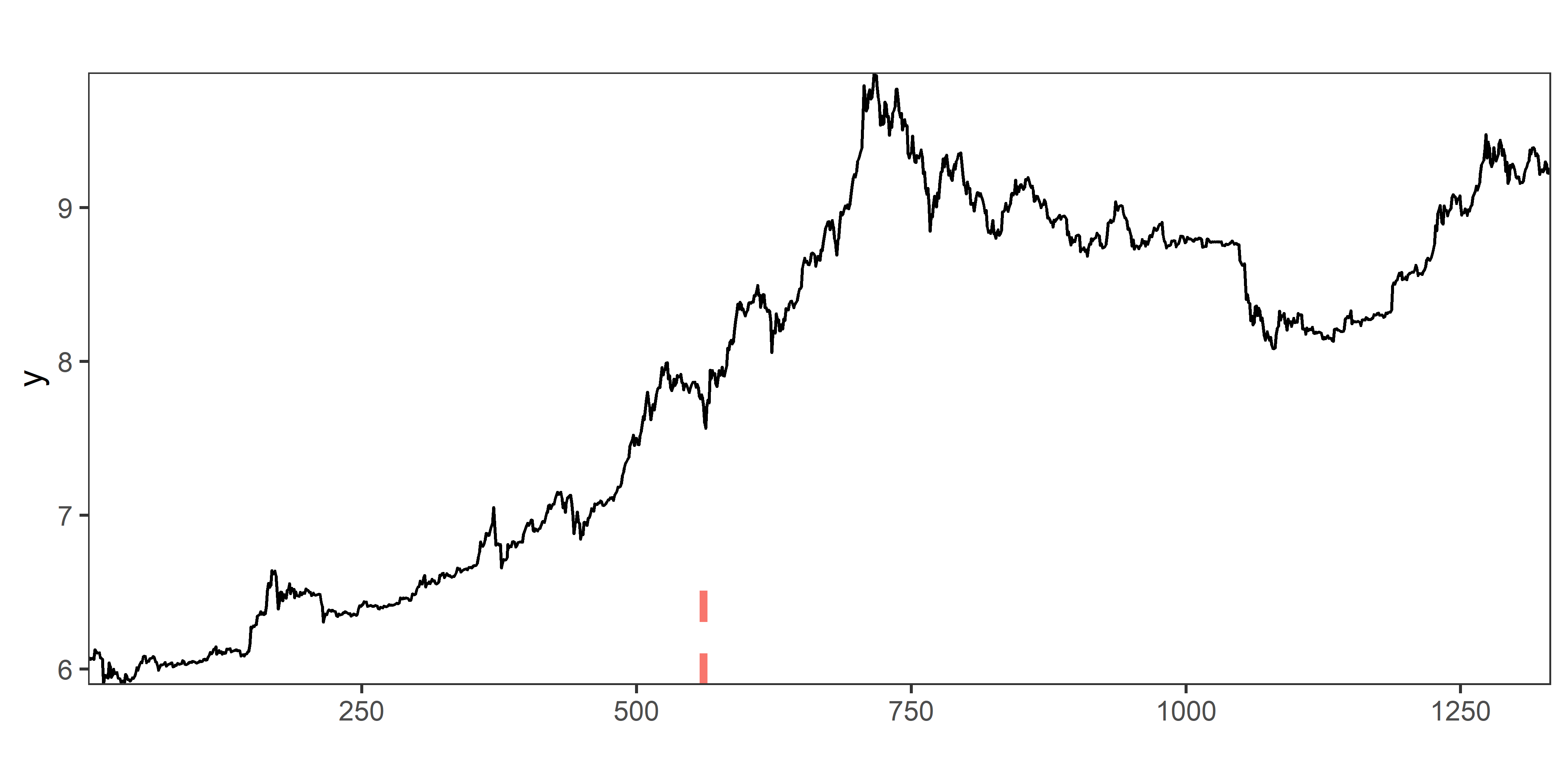
Точка излома тренда, обнаруженная во временном ряду стоимости биткоина с помощью модели BO0

РИСУНОК 8.2: Точка излома тренда, обнаруженная во временном ряду стоимости биткоина с помощью модели BO0

Как видно на рис. 8.2, метод EDM обнаружил одну единственную точку излома тренда (отмечена вертикальной прерывистой линией), что обусловлено принятым по умолчанию аргументом method = "amoc" (см. выше). Для оценивания статистической значимости этого сдвига во временном ряду следует воспользоваться аргументом nperm. Выполним такое оценивание с помощью перестановочного теста с 1000 итераций (выполнение этой команды займет какое–то время):

Объект BO0_perm представляет собой список со следующими элементами:

## $loc
## [1] 561
## 
## $stat
## [1] 107.6948
## 
## $time
## [1] 44.78
## 
## $pval
## [1] 0.000999001

где loc — это положение точки излома (т.е. ее порядковый номер во временном ряду), stat — значение E-критерия, time — время выполнения команды (сек.), а pval — \(p\)–значение, полученное с помощью перестановочного теста. Как видим, обнаруженный сдвиг уровня временного ряда оказался статистически значимым (на уровне значимости 0.05).

Запросим теперь нахождение нескольких точек излома (рис. 8.3):

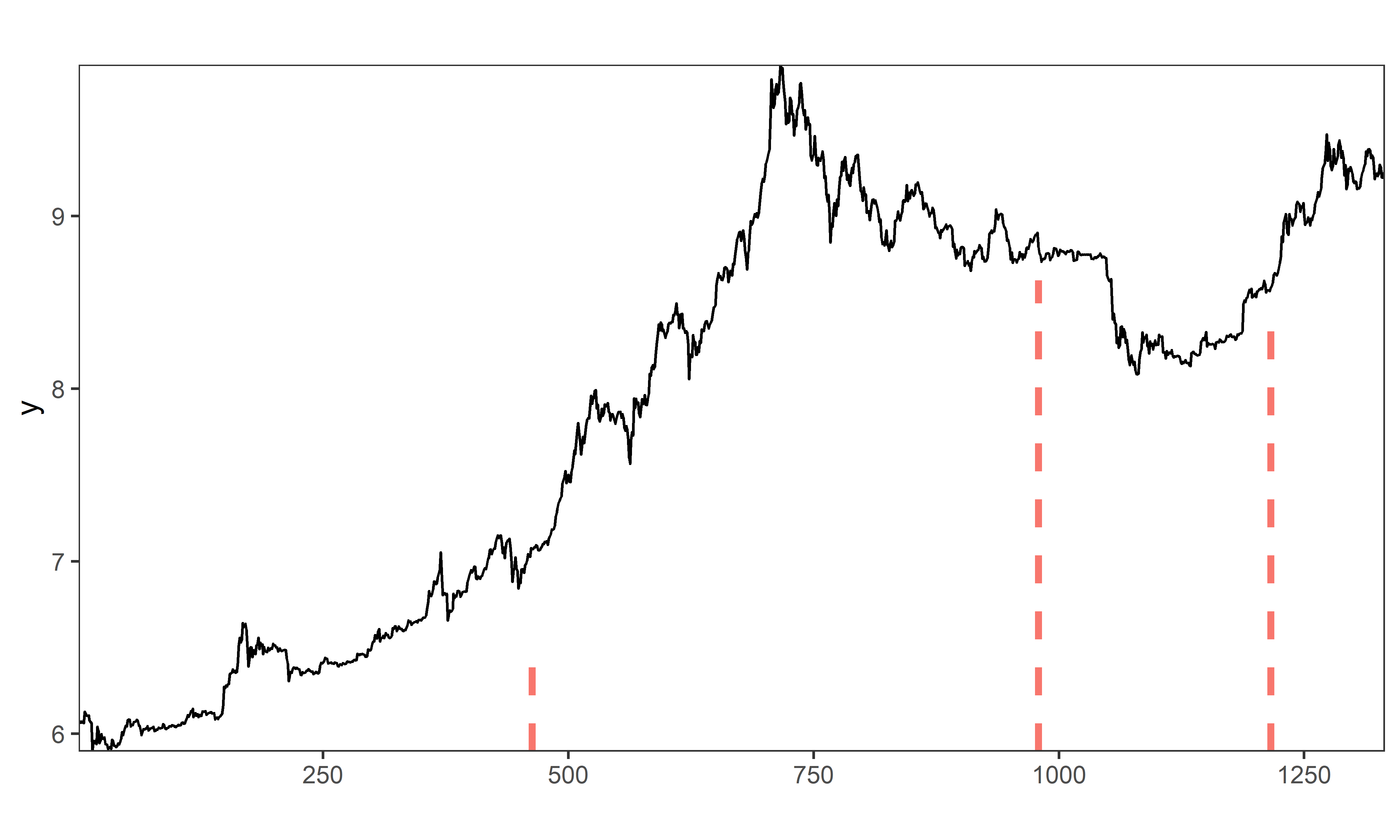
Точки излома тренда, обнаруженные во временном ряду стоимости биткоина с помощью модели BO1

РИСУНОК 8.3: Точки излома тренда, обнаруженные во временном ряду стоимости биткоина с помощью модели BO1

Рассмотрим теперь влияние параметров регуляризации. Сначала отключим регуляризацию с помощью параметра degree = 0 (рис. 8.4):

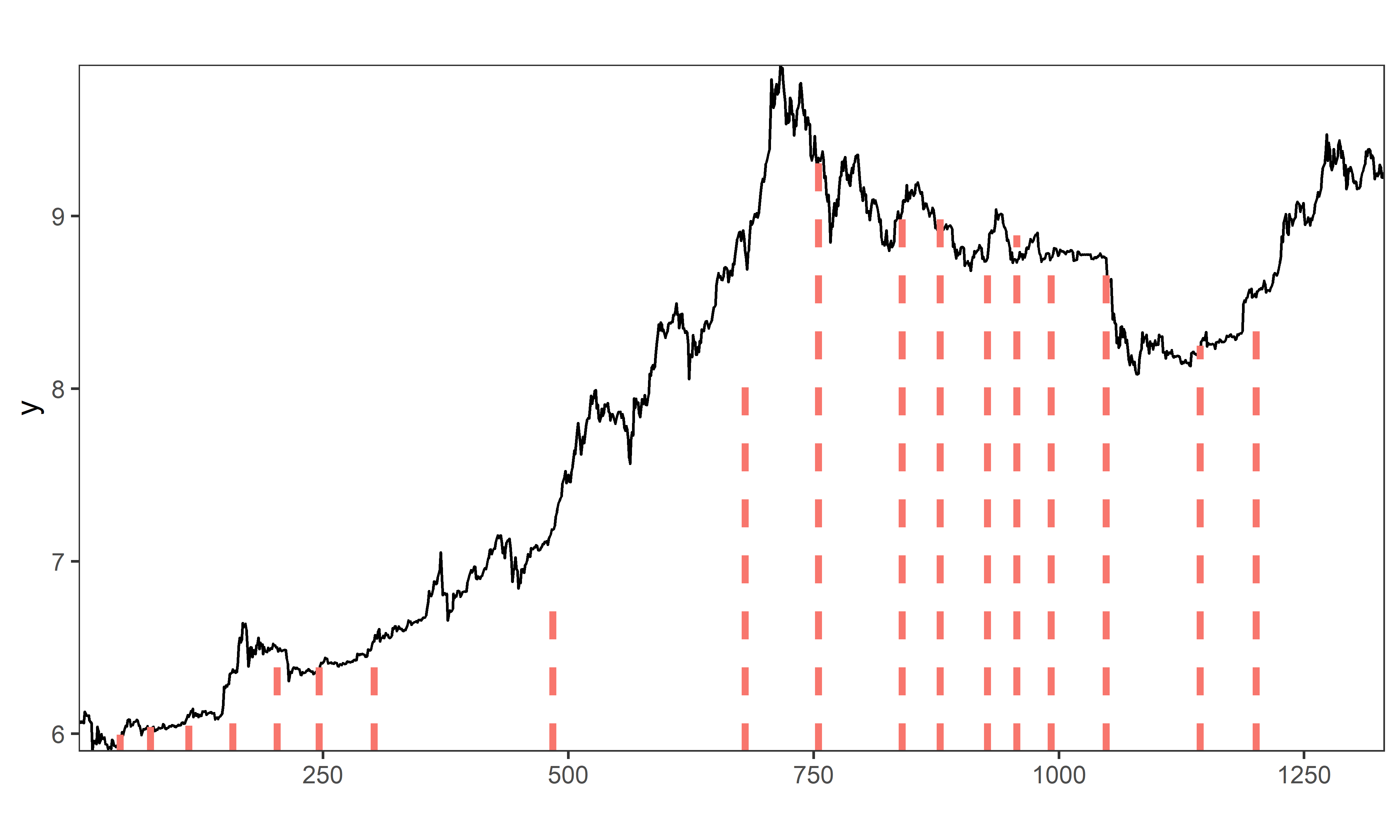
Точки излома тренда, обнаруженные во временном ряду стоимости биткоина с помощью модели BO2

РИСУНОК 8.4: Точки излома тренда, обнаруженные во временном ряду стоимости биткоина с помощью модели BO2

Как было отмечено выше, порядковые номера наблюдений, соответствующих обнаруженным точкам излома, хранятся в элементе loc получаемого объекта–списка:

##  [1]   43   74  113  158  203  246  302  484  680  755  840  879  927  957  992
## [16] 1048 1144 1201

Похожего эффекта (увеличение количества обнаруженных точек излома) можно добиться также с помощью низкого значения параметра percent (рис. 8.5):

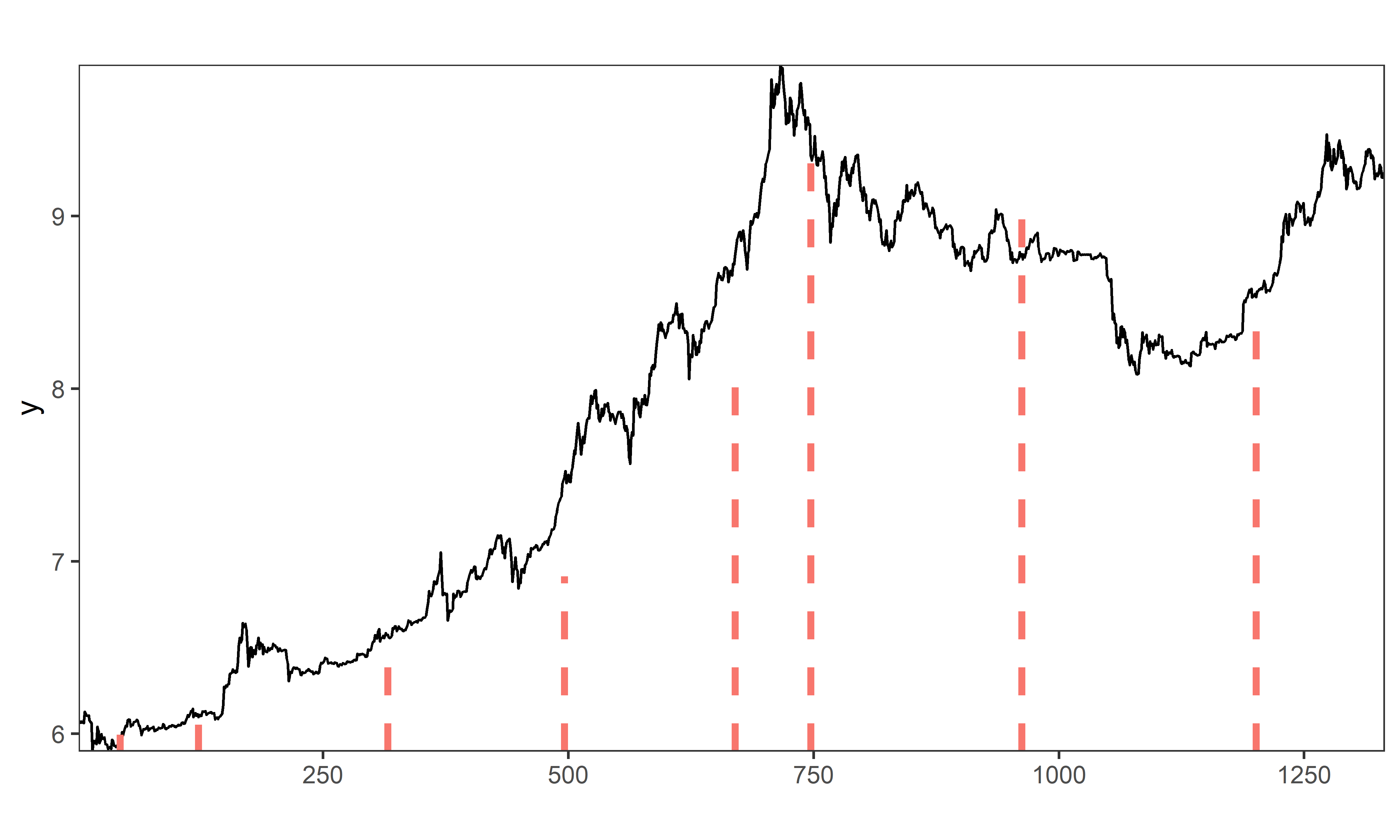
Точки излома тренда, обнаруженные во временном ряду стоимости биткоина с помощью модели BO3

РИСУНОК 8.5: Точки излома тренда, обнаруженные во временном ряду стоимости биткоина с помощью модели BO3

Наконец, снижение параметра beta тоже приведет к увеличению числа обнаруженных алгоритмом точек излома (рис. 7):

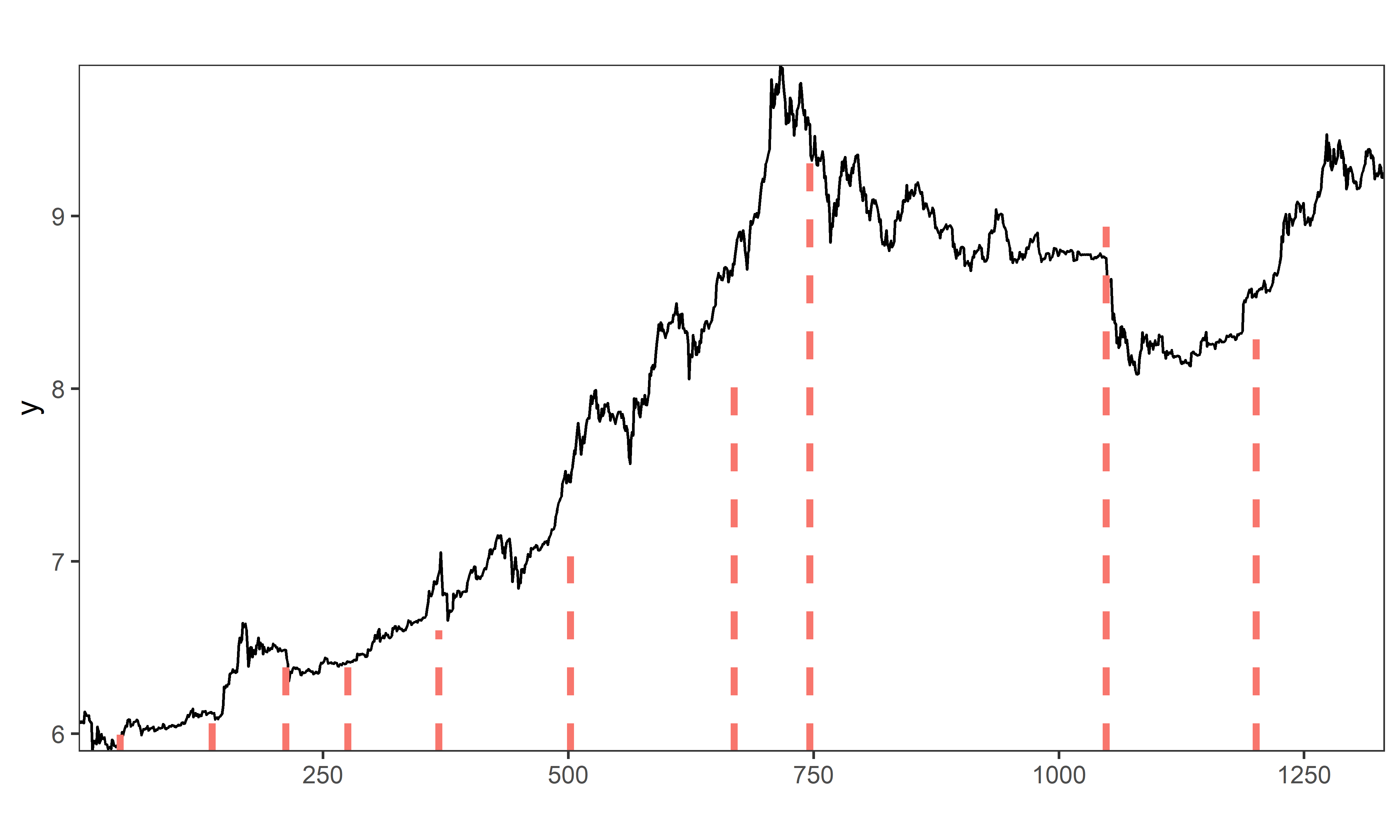
Точки излома тренда, обнаруженные во временном ряду стоимости биткоина с помощью модели BO4

РИСУНОК 8.6: Точки излома тренда, обнаруженные во временном ряду стоимости биткоина с помощью модели BO4

Итак, мы рассмотрели принципы работы с пакетом BreakoutDetection, в котором реализован один из наиболее эффективных методов обнаружения структурных изменений во временных рядах — “E-Divisive with Medians”. Как было отмечено выше, этот метод особенно хорошо подходит для использования в автоматических системах мониторинга параметров технических систем (именно для этого он изначально был разработан в компании Twitter). Другие примеры, где EDM может оказаться полезным, включают:

  • анализ результатов, полученных в ходе A/B тестирования (аргумент method со значением "amoc" позволит оценить влияние экспериментального фактора на сдвиг интересующей исследователя переменной–отклика);
  • обнаружение изменений в переменных, описывающих поведение людей (например, активность в социальных сетях) или животных и т.п.

Хотя пакет BreakoutDetection очень прост в использовании и дает надежные результаты, следует отметить, что он, к сожалению, не обновлялся с 2014 г. Об этом стоит помнить, если вы решите использовать его в своих проектах.