ГЛАВА 13 Кластеризация по результатам подгонки моделей
Как было отмечено в гл. 10, один из способов кластеризации временных рядов основан на подгонке модели с определенной фиксированной структурой к каждому из анализируемых рядов и последующему использованию оцененных параметров модели в качестве описательных признаков. Для демонстрации этого принципа предположим, что временные ряды из набора данных cryptos были порождены процессом, который можно хорошо аппроксимировать байесовской структурной моделью с линейным локальным трендом и авторегрессионной компонентой первого порядка (гл. 7). На рис. 13.1 показан результат подгонки такой модели к четырем случайно выбранным временным рядам из набора данных cryptos.
require(dplyr)
require(ggplot2)
require(tidyr)
require(bsts)
# Вспомогательная функция для подгонки моделей:
fit_bsts <- function(y) {
ss <- AddLocalLinearTrend(list(), y)
ss <- AddAr(ss, y, lag = 1)
m <- bsts(y, ss, niter = 1500, ping = 0, seed = 42)
return(m)
}
# Вспомогательная функция для извлечения наиболее
# вероятных модельных значений стоимости криптовалюты:
get_bsts_fit <- function(m) {
burn <- SuggestBurn(0.1, m)
m$state.contributions %>%
apply(., MARGIN = 3, FUN = rowSums) %>%
.[-(1:burn), ] %>% colMeans()
}
# Подгонка моделей (займет какое-то время) и
# сопутствующие вычисления:
set.seed(101)
cryptos_bsts_fit <- cryptos %>%
filter(coin %in% sample(unique(coin), size = 4)) %>%
mutate(y = log(y)) %>%
pivot_wider(names_from = coin, values_from = y) %>%
arrange(ds) %>%
dplyr::select(-ds) %>%
lapply(., fit_bsts) %>%
lapply(., function(x) {
fit <- get_bsts_fit(x)
x[['fit']] <- fit
return(x)
}) %>%
lapply(., function(x) {
tibble(idx = 1:length(x$fit),
y = as.numeric(x$original.series), fitted_y = x$fit)
}) %>%
bind_rows(., .id = "coin")
# Визуализация результатов подгонки моделей
cryptos_bsts_fit %>%
ggplot() +
geom_point(aes(idx, y), col = "skyblue", alpha = 0.3) +
geom_line(aes(idx, fitted_y)) +
theme_minimal() + facet_wrap(~coin, scales = "free_y")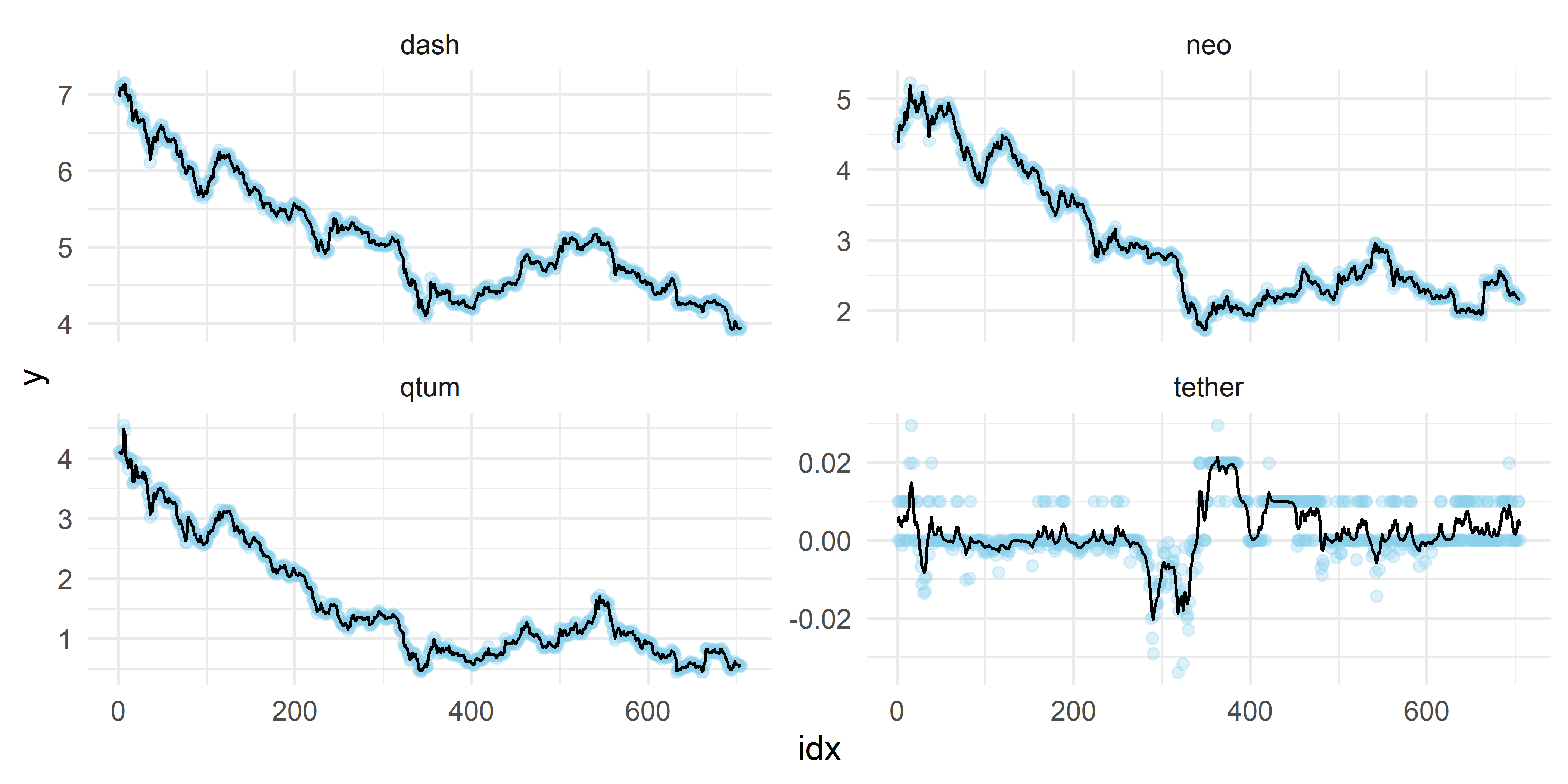
РИСУНОК 13.1: Пример подгонки байесовской структурной модели с одинаковым набором компонент к четырем случайно выбранным временным рядам из таблицы cryptos. Синими полупрозрачными точками показаны обучающие данные. Черные линии соответствуют аппроксимированным модельным значениям
Для кластеризации временных рядов cryptos мы воспользуемся несколькими количественными показателями, которые можно извлечь и bsts–объектов в готовом виде или рассчитать самостоятельно. Ниже приведен код функции, которая поможет нам выполнить подгонку модели к каждому временному ряду и получить необходимые показатели в табличном виде:
get_bsts_features <- function(df) {
# спецификация и подгонка модели
y <- df$y
ss <- AddLocalLinearTrend(list(), y)
ss <- AddAr(ss, y, lag = 1)
m <- bsts(y, ss, niter = 1500, ping = 0, seed = 42)
# извлечение готовых показателей и добавление их в таблицу:
s <- summary(m)
result <- tibble(
residual_sd = s$residual.sd,
prediction_sd = s$prediction.sd,
r_square = s$rsquare,
harvey_stat = s$relative.gof,
trend_level_sigma_mean = mean(m$sigma.trend.level),
trend_level_sigma_sd = sd(m$sigma.trend.level),
trend_slope_sigma_mean = mean(m$sigma.trend.slope),
trend_slope_sigma_sd = sd(m$sigma.trend.slope),
ar1_coef_mean = mean(m$AR1.coefficients),
ar1_coef_sd = sd(m$AR1.coefficients),
ar1_sigma_mean = mean(m$AR1.sigma),
ar1_sigma_sd = sd(m$AR1.sigma),
final_state_mean = m$final.state %>% rowSums() %>% mean(),
final_state_sd = m$final.state %>% rowSums() %>% sd(),
loglik_mean = mean(m$log.likelihood),
loglik_sd = sd(m$log.likelihood)
)
return(result)
}Применим функцию get_bsts_features к таблице cryptos (выполнение этого кода займет около 5 минут):
Для кластеризации анализируемых временных рядов на основе полученных описательных признаков воспользуемся методом \(k\) средних c \(k=4\) (предварительно выполнив стандартизацию данных и применив метод PCA для удаления корреляции между отдельными признаками):
set.seed(42)
pca_bsts_features <- cryptos_bsts_features %>%
dplyr::select(-coin) %>%
prcomp(scale = TRUE)
# Первые пять главных компонент объясняют примерно 97%
# исходной дисперсии данных (результат не приводится
# для экономии места):
# summary(pca_bsts_features)
# Кластеризация:
set.seed(1984)
cl_bsts <- cryptos_bsts_features %>%
dplyr::select(coin) %>%
bind_cols(., as_tibble(pca_bsts_features$x)) %>%
dplyr::select(PC1:PC5) %>%
kmeans(., centers = 4, nstart = 50)Изобразим теперь исходные временные ряды, сгруппировав их в соответствии с результатами выполненного кластерного анализа:
require(ggrepel)
cryptos_bsts_features %>%
mutate(cluster = paste0("C", cl_bsts$cluster)) %>%
dplyr::select(coin, cluster) %>%
inner_join(., cryptos, by = "coin") %>%
group_by(coin) %>%
mutate(label = ifelse(ds == max(ds), coin, NA)) %>%
ggplot(., aes(ds, y, group = coin)) +
geom_line() +
geom_text_repel(aes(label = label),
size = 3, nudge_x = 50, segment.size = 0.4,
segment.color = "gray60", point.padding = 0.2,
force = 4, na.rm = TRUE) +
scale_y_log10() +
facet_wrap(~cluster, scales = "free_y") +
theme_minimal() +
xlim(c(as.Date("2018-01-01"), as.Date("2020-08-01")))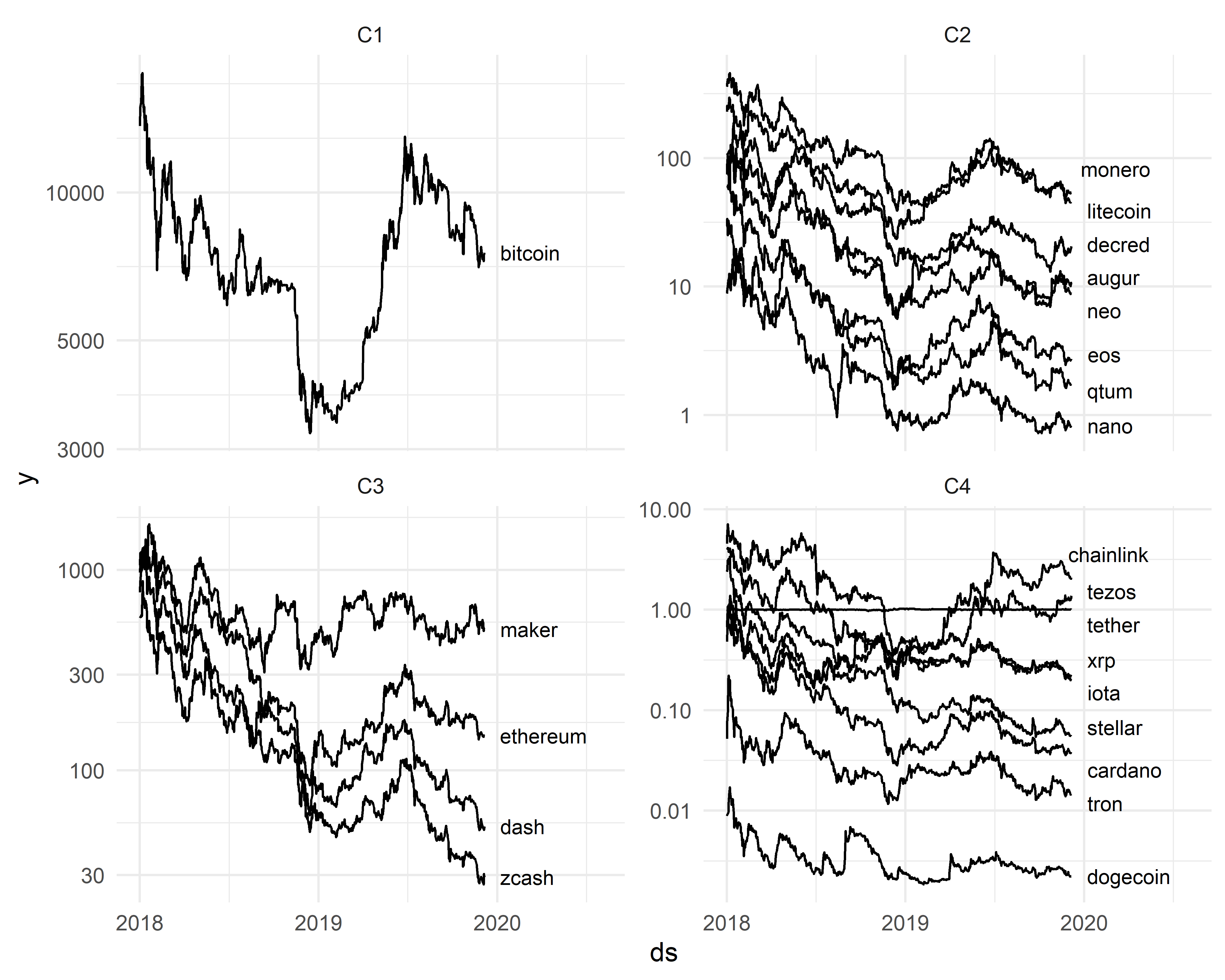
РИСУНОК 13.2: Результат кластеризации временных рядов из таблицы cryptos по методу \(k\) средних на основе количественных показателей bsts–моделей
Представленный на рис. 13.2 результат заметно отличается от выполненных нами ранее кластеризаций на основе исходных данных (гл. 11) и по описательным признакам (гл. 12). Это наблюдение еще раз подчеркивает необходимость применения нескольких вариантов кластеризации для нахождения решения, которое имеет смысл с т.з. его дальнейшего практического использования.