ГЛАВА 7 Пакет bsts
Эта глава посвящена еще одному мощному инструменту для моделирования и прогнозирования временных рядов — пакету bsts, который был разработан сотрудником компании Google Стивеном Скоттом (Steven L. Sсott). В основе этого пакета лежит методология, известная в литературе под несколькими названиями: “байесовские структурные модели временных рядов” (Bayesian structural time series models), “модели пространства состояний” (state-space models), “динамические линейные модели” (dynamic linear models), модели на основе фильтра Калмана (Kalma filter models) и др. Подобно пакету prophet, bsts делает упор на прогнозирование временных рядов, представленных дневными данными, и позволяет включать в модели сторонние предикторы (в частности, эффекты “праздников”). Оба пакета используют принципы байесовской статистики для оценивания параметров моделей. Однако в отличие от пакета prophet, который выполняет подгонку единой обобщенной аддитивной модели (см. разд. 6.1), в пакете bsts происходит байесовское усреднение предсказаний ансамбля, состоящего из большого количества моделей. Лежащая в основе bsts методология является более общей и гибкой.
7.1 Методология
Полное изложение реализованной в пакете bsts методологии можно найти в статье Scott and Varian (2014). Здесь мы ограничимся лишь кратким ее описанием, необходимым для уверенной работы с функциями этого пакета и их параметрами.
Пусть \(y_t\) — это значение некоторой количественной переменной, учтенной в момент времени \(t\). Структурная модель временного ряда задается двумя уравнениями: \[\begin{aligned} & y_t = Z_{t}^\intercal \alpha_t + \epsilon_t \qquad \epsilon_t \sim \mathcal{N}(0, H_T),\\ & \alpha_{t+1} = T_t\alpha_t + R_t\eta_t \qquad \eta_t \sim \mathcal{N}(0, Q_T). \end{aligned}\]
Предполагается, что в каждый момент времени \(t\) изучаемая динамическая система может находится в некотором ненаблюдаемом в явном виде (латентном) состоянии \(\alpha_t\). Первое из приведенных уравнений связывает наблюдаемые данные с вектором таких латентных состояний и называется уравнением наблюдений (observation equation). Второе уравнение задает процесс перехода из одного латентного состояния в другое и называется уравнением переходов (transition equation). Состояние системы в каждый момент времени определяется только ее состоянием в предыдущий момент, т.е. динамика системы имеет марковский характер (рис. 7.1). Остатки \(\epsilon_t\) и \(\eta_t\) независимы друг от друга и имеют нормальное распределение со средним 0. Матрицы \(Z_t\), \(T_t\) и \(R_t\) называются структурными параметрами и обычно содержат как известные значения (индикаторные переменные 1 и 0), так и неизвестные параметры. Модели, которые можно описать с помощью приведенных двух уравнений, называют моделями пространства состояний. В этой форме можно представить очень широкий круг моделей, включая, например, все разновидности ARIMA (Цыплаков 2011).

РИСУНОК 7.1: Схематичное представление модели пространства состояний для конечного временного ряда с \(T\) наблюдениями (см. объяснения в тексте)
Структурные модели временных рядов — это одно из семейств моделей пространства состояний. В структурных моделях временной ряд представлен в виде суммы ненаблюдаемых компонент, которые можно интерпретировать как тренд, сезонность, эффекты предикторов и т.д. Эти компоненты служат своего рода “строительными блоками”, которые исследователь может сочетать в соответствии с решаемой задачей и особенностями данных. Так, для временных рядов базовую структурную модель (basic structural model) с предикторами можно представить следующим образом: \[ \begin{aligned} & y_t = \underbrace{\mu_t}_{\text{тренд}} + \underbrace{\gamma_t}_{\text{сезонность}} + \underbrace{\beta^\intercal \boldsymbol{x}_t}_{\text{предикторы}} + \epsilon_t,\\ & \mu_{t} = \mu_{t-1} + \delta_{t-1} + u_t,\\ & \delta_{t} = \delta_{t-1} + v_t,\\ & \gamma_{t} = -\sum_{s=1}^{S-1} \gamma_{t-s} + w_t, \end{aligned}\] где \(\mu_{t}\) — это текущее значение тренда модели, а \(\delta_t\) — его коэффициент прироста. Сезонная компонента \(\gamma_t\) представлена в виде \(S-1\) индикаторных переменных с изменяющимися во времени коэффициентами. В данном случае \(\eta_t = (u_t, v_t, w_t)\) объединяет независимые нормально распределенные случайные колебания, \(Q_T\) — диагональная матрица, диагональ которой содержит \(\sigma_{u}^2\), \(\sigma_{v}^2\) и \(\sigma_{w}^2\), а \(H_T\) — это скаляр \(\sigma_{\epsilon}^2\). Оцениванию на основе данных подлежат дисперсии \(\sigma_{u}^2\), \(\sigma_{v}^2\), \(\sigma_{w}^2\), \(\sigma_{\epsilon}^2\), а также коэффициенты регрессии \(\beta\).
Подгонка структурных моделей временных рядов выполняется с использованием фильтра Калмана и метода Монте–Карло по схеме марковских цепей (Markov Chain Monte Carlo, MCMC). Для оценивания и одновременной регуляризации коэффициентов регрессии применяется т.н. метод “spike–and–slab” (найти подходящий аналог этому термину на русском языке сложно, поэтому оставим его без перевода). Вкратце, этот метод заключается в присваивании каждому коэффициенту регрессии определенной высокой априорной вероятности того, что он равен нулю (“вероятность включения” в модель, inclusion probability). Используя наблюденные данные и теорему Байеса, вероятности включения обновляют. В дальнейшем при MCMC–сэмплировании коэффициентов из полученных апостериорных распределений многие симулированные коэффициенты оказываются в точности равными нулю. Такой механизм регуляризации позволяет эффективно выполнить селекцию наиболее важных предикторов и параллельно избавиться от мультиколлинеарности, благодаря чему в байесовские структурные модели можно включать большое количество предикторов без риска переобучения.
7.2 Функция bsts()
Функция bsts() генерирует упомянутые выше MCMC–выборки параметров структурных моделей временных рядов из соответствующих апостериорных распределений. Эта функция имеет следующие аргументы:
formula— стандартная для R формула модели. Если предикторы в модели отсутствуют, то вместо формулы можно просто указать числовой вектор со значениями моделируемого временного ряда или объект классаzoo,xtsилиts. Зависимая переменная может содержать пропущенные значения, но предикторы — нет.state.specification— список, элементы которого содержат спецификации компонент модели. Эти спецификации создаются с помощью функций, чье имя начинается с приставкиAdd(например,AddLocalLinerTrend(),AddSeasonal(),AddAr()— см. примеры ниже).family— параметр, определяющий “семейство” создаваемой модели в обычном для R смысле. По умолчанию предполагается, что моделируемая зависимая переменная является количественной и что ее остатки имеют гауссово распределение ("gaussian"). Кроме того, в пакетеbstsимеется возможность моделировать счетные (family = "poisson") и бинарные отклики (family = "logit"), а также количественные переменные, в которых имеют место наблюдения–выбросы (family = "student"). Бинарный отклик можно подать в виде вектора со значениями0/1,TRUE/FALSEили-1/1. Если бинарный отклик представлен числом положительных и отрицательных исходов, то его подают в виде матрицы с двумя столбцами (в первом столбце содержатся положительные исходы). Отклик со счетными данными (family = "poisson"), зарегистрированными в учетных единицах одинакового размера (например, на 1 м2) или продолжительности (например, за 1 ч), подают в виде вектора. Если же регистрация таких данных была выполнена в учетных единицах разного размера или продолжительности, то отклик подают в виде матрицы с двумя столбцами, первый из которых содержит результаты подсчета, а второй — размер или продолжительность учетной единицы.data— необязательный аргумент, задающий объект (таблица, список или окружение) с переменными, которые входят в формулу модели (аргументformula).prior— список с информацией об априорных распределениях предикторов, созданный с помощью функцииSpikeSlabPrior(). Этот аргумент нужен только если предикторы входят в формулу модели. Если предикторов в модели нет, то аргументpriorбудет просто соответствовать априорному распределению стандартного отклонения остатков, которое можно задать самостоятельно с помощью функцииSdPrior(). Обычно в этом аргументе нет необходимости, поскольку хорошие результаты получаются и с его принятыми по умолчанию настройками.contrasts— матрица контрастов модели. Этот аргумент идентичен такому же аргументу базовой функцииlm().na.action— задает правило обработки пропущенных наблюдений в зависимой переменной. По умолчанию пропущенные наблюдения допускаются. Для их удаления на этот аргумент необходимо подать либо функциюna.omit(), либо функциюna.exclude()(без скобок, т.е.na.action = na.omit).niter— положительное целое число, задающее количество итераций алгоритма MCMC.ping— число, задающее частоту вывода на экран служебной информации о ходе выполнения алгоритма MCMС. Если это положительное число, то информация будет выводиться каждыеpingитераций.model.options— настройки вычислительных алгоритмов, лежащих в основе функцииbsts, которые можно задать с помощью функцииBstsOptions(). Необходимость в изменении этих настроек возникает очень редко.timestamps— временные отметки регистрации значений моделируемой переменной. Этот аргумент бывает полезным, когда в данных имеются пропущенные значения, или когда на одну временную метку приходится несколько наблюдений зависимой переменной. Если в моделируемом временном ряду пропущенные значения отсутствуют и на каждую временную отметку приходится только одно наблюдение, то этот аргумент становится необязательным (по умолчанию он равенNULL).seed— зерно генератора случайных чисел (для воспроизводимости результатов вычислений)....— дополнительные аргументы, которые передаются на функциюSpikeSlabPrior()(см. аргументpriorвыше).
Функция bsts() возвращает объект класса bsts, который представляет собой список с несколькими элементами. Содержимое этого списка определяется спецификацией конкретной модели, но как минимум он включает следующие элементы:
state.specification— информация о компонентах модели, заданных с помощью одноименного аргумента функцииbsts();state.contributions— массив со значениями компонент модели, оцененными в ходе каждой изniterMCMC–итераций;one.step.prediction.errors— матрица сniterстроками, содержащая т.н. “ошибки следующего шага” (см. объяснение в разд. 7.4);sigma.obs— вектор длинойniterсо стандартными отклонениями остатков модели;log.likelihood— вектор длинойniterсо значениями логарифма функции максимального правдоподобия модели.
У объектов класса bsts есть несколько методов, включая стандартные summary(), plot() и predict(). Примеры использования этих методов приведены ниже.
7.3 Спецификация компонент модели
Пакет bsts содержит целую библиотеку функций, формирующих различные компоненты структурных моделей временных рядов. Как было отмечено выше, имена всех этих функций начинаются с приставки Add, поскольку они “добавляют” спецификацию тех или иных компонент в соответствующий список. Этот список (обычно ему дают имя ss, что значит “state specification”, т.е. “спецификация состояний”) далее подается на функцию bsts(), которая непосредственно выполняет подгонку структурной модели. Основными аргументами Add–функций являются state.specification — список, в который необходимо добавить спецификацию соответствующей компоненты, и y — вектор со значениями моделируемой переменной. Приведенный ниже код поможет понять, как это работает:
require(bsts)
y <- rnorm(100)
# список со спецификациями компонент модели:
ss <- list()
ss <- AddLocalLevel(state.specification = ss, y = y)
# ...или просто ss <- AddLocalLevel(ss, y)
ss <- AddAr(ss, y, lags = 1)
# подгонка модели:
model <- bsts(y, state.specification = ss, niter = 1500) Ниже перечислены наиболее важные Add–функции и соответствующие им компоненты структурных моделей (сравните с описанной выше базовой структурной моделью временных рядов).
AddLocalLevel()— локальный уровень (local level), соответствующий процессу “случайного блуждания с шумом” (random walk with noise): \[ \begin{aligned} & y_t = \mu_t + \epsilon_t,\\ & \mu_{t} = \mu_{t-1} + u_t,\\ & \epsilon_t \sim \mathcal{N}(0, \sigma_{\epsilon}^2), u_t \sim \mathcal{N}(0, \sigma_{u}^2) \end{aligned} \]AddAr()— авторегрессионный процесс (autoregressive process), согласно которому текущий средний уровень временного ряда линейно связан с его предыдущими значениями (вплоть до временного сдвига \(p\), который называют также порядком процесса): \[ \begin{aligned} & y_t = \mu_t + \epsilon_t,\\ & \mu_{t} = \sum_{i=1}^{p}\phi_i \mu_{t-i} + u_t,\\ & \epsilon_t \sim \mathcal{N}(0, \sigma_{\epsilon}^2), u_t \sim \mathcal{N}(0, \sigma_{u}^2), \end{aligned} \] где \(\phi_1, \dots, \phi_{p}\) — подлежащие оцениванию параметры модели. Для работы с большими значениями \(p\) в пакетеbstsесть специальная функцияAddAutoAr(), которая применяет метод “spike–and–slab” для регуляризации \(\phi_1, \dots, \phi_{p}\) (т.е. многие из этих параметров в итоге окажутся в точности равными нулю).AddLocalLinearTrend()— локальный линейный тренд (local linear trend). Предполагает, что процессом “случайного блуждания” можно описать динамику как среднего уровня временного ряда \(\mu_t\), так и коэффициента его прироста \(\delta_t\) (“угол наклона” тренда): \[ \begin{aligned} & y_t = \mu_t + \epsilon_t,\\ & \mu_{t} = \mu_{t-1} + \delta_{t-1} + u_t,\\ & \delta_{t} = \delta_{t-1} + v_t,\\ & \epsilon_t \sim \mathcal{N}(0, \sigma_{\epsilon}^2), u_t \sim \mathcal{N}(0, \sigma_{u}^2), v_t \sim \mathcal{N}(0, \sigma_{v}^2) \end{aligned} \]AddStudentLocalLinearTrend()— устойчивый локальный линейный тренд (robust local linear trend). Отличается от предыдущей компоненты тем, что ее случайные колебания подчиняются распределению Стьюдента, а не Гаусса. Эта компонента хорошо подходит для краткосрочных прогнозов на основе временных рядов, в которых иногда наблюдаются резкие скачки среднего уровня. Распределенные по Стьюденту остатки можно ввести также в уравнение наблюдений структурной модели (см. выше), подав аргументfamily = "student"на функциюbsts(). Как было отмечено выше, это позволит получать более надежные прогнозы в присутствии аномальных наблюдений.AddSemiLocalLinearTrend()— полулокальный линейный тренд. Похож на модель локального уровня, но предполагает, что коэффициент прироста среднего уровня ряда развивается в соответствии с авторегрессионным процессом первого порядка: \[ \begin{aligned} & y_t = \mu_t + \epsilon_t,\\ & \mu_{t} = \mu_{t-1} + \delta_{t-1} + u_t,\\ & \delta_{t} = D + \phi \times (\delta_{t-1} - D) + v_t,\\ & \epsilon_t \sim \mathcal{N}(0, \sigma_{\epsilon}^2), u_t \sim \mathcal{N}(0, \sigma_{u}^2), v_t \sim \mathcal{N}(0, \sigma_{v}^2) \end{aligned} \] Стационарный авторегрессионный процесс первого порядка более стабилен, чем процесс случайного блуждания, что делает модель полулокального линейного тренда более подходящей для расчета долгосрочных прогнозов (благодаря меньшей неопределенности в отношении предсказанных значений).AddSeasonal()— сезонная компонента (seasonal component), число сезонов \(S\) в которой задается с помощью аргументаnseasons. В основе этой компоненты лежит линейная модель с \(S-1\) индикаторными переменными: \[ \begin{aligned} & y_t = \gamma_t + \epsilon_t,\\ & \gamma_{t} = -\sum_{s=1}^{S-1} \gamma_{t-s} + w_t,\\ & \epsilon_t \sim \mathcal{N}(0, \sigma_{\epsilon}^2), w_t \sim \mathcal{N}(0, \sigma_{w}^2) \end{aligned} \] Для моделирования физических и других процессов с четко выраженными амплитудой и частотой можно воспользоваться также функциейAddTrig(), которая задает соответствующую компоненту в виде суммы элементарных тригонометрических составляющих (cos и sin) с варьирующими во времени коэффициентами.AddRegressionHoliday()— добавляет в модель эффекты “праздников” и других важных для моделируемого временного ряда событий. Список таких событий формируется с помощью нескольких вспомогательных функций (например,NamedHoliday(),FixedDateHoliday(),DateRangeHolidayи др.) и подается на аргументholiday.listфункцииAddRegressionHoliday(). В основе этой функции лежит простая модель следующего вида: \[ \begin{aligned} & y_t = \beta_{d(t)} + \epsilon_t,\\ & \epsilon_t \sim \mathcal{N}(0, \sigma_{\epsilon}^2), \end{aligned} \] где вектор \(\beta\) содержит коэффициенты регрессии \(\beta_d \sim \mathcal{N}(0, \sigma^2)\).
7.4 Примеры моделей без предикторов
Для иллюстрации основ работы с пакетом bsts мы воспользуемся данными по стоимости номера в гостинице 73738 из таблицы hotels (см. подразд. 1.5.4). Эти данные обладают несколькими свойствами, которые делают задачу прогнозирования достаточно трудной (рис. 7.2):
- крайне нерегулярная регистрация наблюдений с точностью до 1 секунды, что приводит к большому количеству пропущенных значений и “маскировке” возможных сезонных колебаний;
- относительно непродолжительный период учета данных (8 месяцев), что в совокупности с многочисленными пропущенными значениями затрудняет адекватное моделирование тренда и сезонных колебаний.
require(dplyr)
require(ggplot2)
hotels %>%
filter(prop_id == 73738) %>%
ggplot(aes(date_time, price_usd)) +
geom_line() + geom_point(alpha = 0.4) +
scale_y_log10() +
theme_minimal() + ylim(c(0, NA))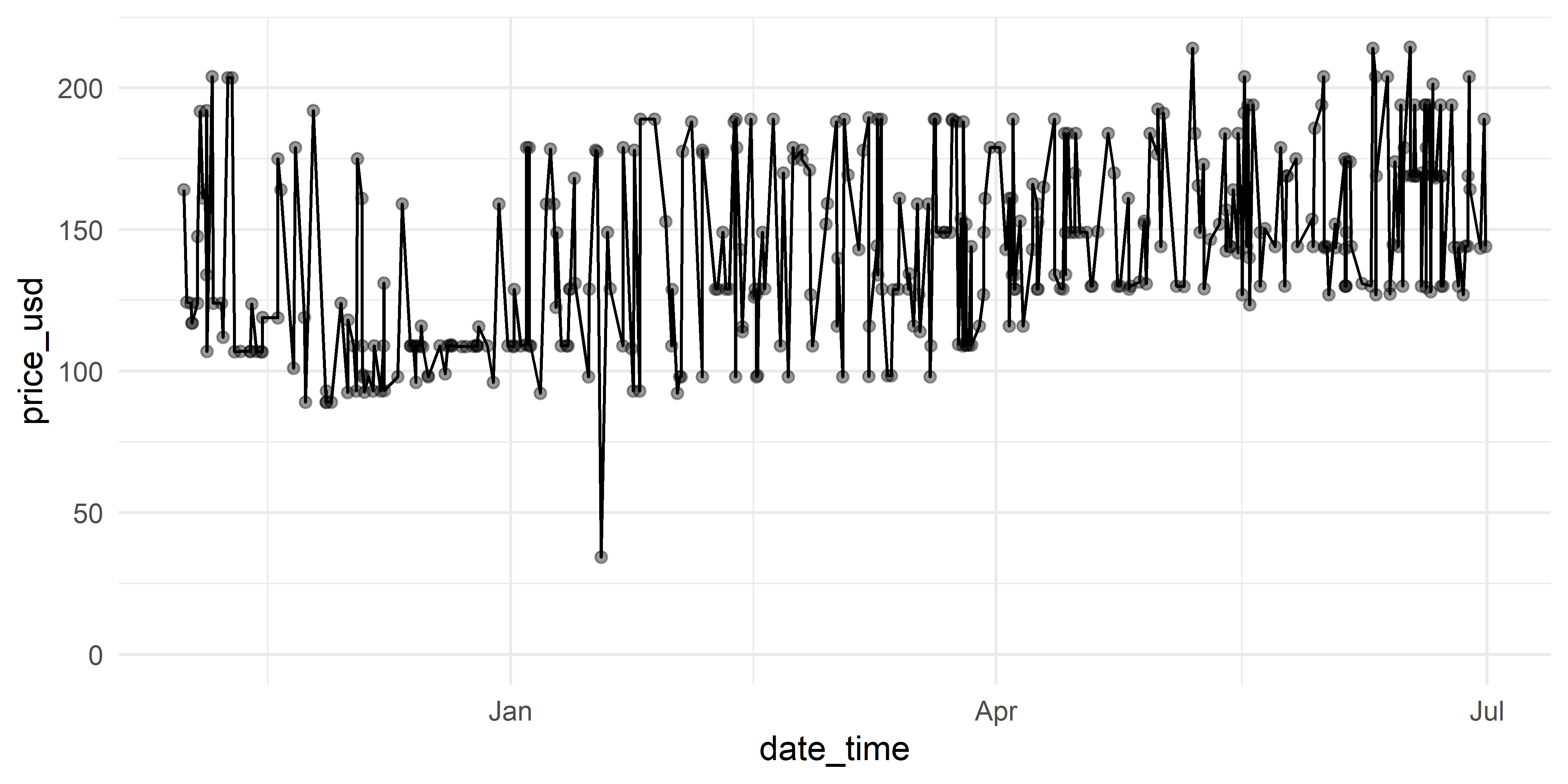
РИСУНОК 7.2: Исходные данные по динамике стоимости номера в гостинице 73738 из таблицы hotels
Перечисленные трудности можно отчасти преодолеть путем агрегирования данных с секундного до некоторого более крупного интервала времени (например, путем расчета средней стоимости номера, зарегистрированной за минуту, час, день и т.п.). Выбор подходящего интервала для агрегирования — это отдельная задача, которая, к сожалению, не имеет простого решения. С одной стороны, чем шире интервал (например, дневной), тем меньше в агрегированных данных будет пропущенных наблюдений, но некоторые свойства исходных данных при этом будут утрачены (в частности, внутридневные колебания стоимости). С другой стороны, агрегирование по более узкому интервалу поможет сохранить свойства исходных данных, но не решит проблему большого количества пропущенных наблюдений.
В приведенных ниже примерах агрегирование выполнено путем усреднения логарифмированных значений стоимости гостиничного номера за день. Даже при таком подходе в данных все еще остается несколько пропущенных наблюдений. Хотя лежащая в основе пакета bsts методология достаточно устойчива к наличию небольшого количества пропущенных наблюдений в зависимой переменной, для упрощения примеров мы выполним простую линейную интерполяцию этих пропусков в обучающей выборке, как это было сделано в гл. 4. Проверочная выборка будет содержать 14 наблюдений, что соответствует прогнозному горизонту длиной 14 дней (рис. 7.3).
# Агрегирование данных:
h73738 <- hotels %>%
filter(prop_id == 73738) %>%
index_by(dt = as.Date(date_time)) %>%
summarise(y = mean(log(price_usd))) %>%
tsibble::fill_gaps()
# Разбиение на обучающую и проверочную выборки
# (прогнозный горизонт составляет 14 дней):
cut_point <- as.Date(max(h73738$dt)) - 14
h73738_train <- h73738 %>%
filter(as.Date(dt) <= cut_point) %>%
mutate(y = forecast::na.interp(y))
h73738_test <- h73738 %>%
filter(as.Date(dt) > cut_point)
# Визуализация агрегированных данных:
rbind(mutate(h73738_train, dataset = "train"),
mutate(h73738_test, dataset = "test")) %>%
ggplot(aes(dt, y, col = dataset)) +
geom_line() + geom_point(alpha = 0.4) +
theme_minimal() +
scale_color_manual(values = c("blue", "black"))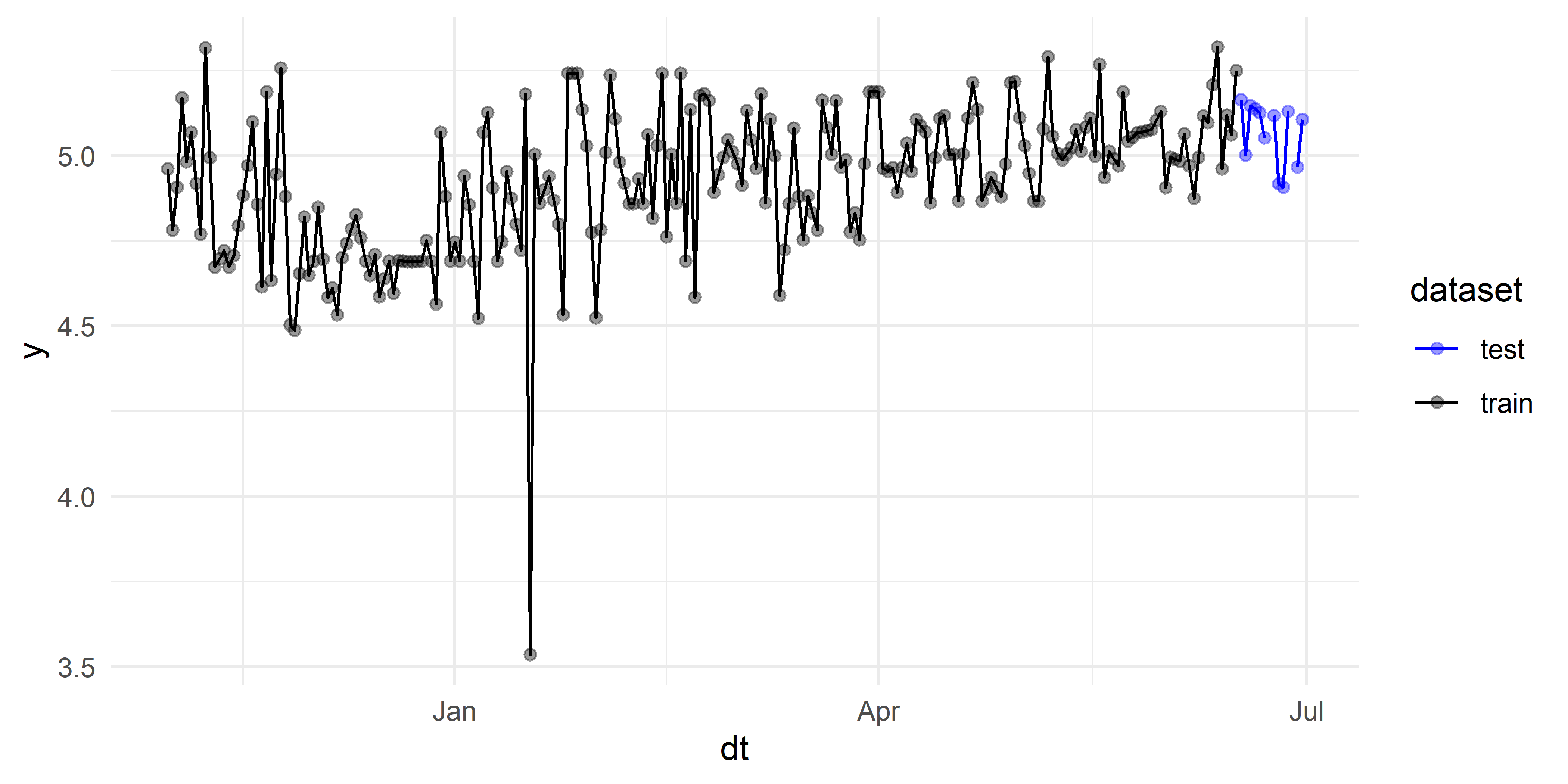
РИСУНОК 7.3: Обучающие (черный цвет) и проверочные (синий цвет) данные по динамике среднедневной стоимости номера в гостинице 73738. Пропуски в обучающих данных восстановлены путем интерполяции. К проверочным данным такое восстановление не применялось, в связи с чем соединяющая точки линия имеет два разрыва
На рис. 7.3 виден слабый возрастающий тренд в данных, который мы попытаемся отразить в модели с помощью компоненты линейного локального тренда (функция AddLocalLinearTrend()). Кроме того, мы добавим в модель компоненту недельной сезонности (функция AddSeasonal(nseasons = 7)), поскольку дневные данные часто демонстрируют такого рода колебания:
require(bsts)
# Моделируемая переменная:
y_73738 <- h73738_train$y
# временные отметки для аргумента `timestamps` функции `bsts()`
# (не обязательны, но полезны для построения графиков):
dt_73738 <- h73738_train$dt
# Спецификация компонент модели:
ss <- list()
ss <- AddLocalLinearTrend(ss, y_73738)
ss <- AddSeasonal(ss, y_73738, nseasons = 7)
# Подгонка модели (может занять некоторое время).
# Результат сохранен в объект с именем `M19`
# (в продолжение нумерации модельных объектов,
# начатой в главе о пакете `prophet`):
M19 <- bsts(y_73738, ss,
timestamps = dt_73738,
niter = 1500, ping = 0, seed = 42)Полученный объект M19 обладает рядом удобных методов, позволяющих исследовать свойства полученной модели. Так, стандартный метод summary() возвращает список с несколькими количественными метриками качества модели, рассчитанными по обучающим данным:
## $residual.sd
## [1] 0.174605
##
## $prediction.sd
## [1] 0.1956826
##
## $rsquare
## [1] 0.3094038
##
## $relative.gof
## [1] 0.3437019В приведенном списке residual.sd — это среднее значение апостериорного распределения стандартного отклонения остатков модели, а rsquare — обычный коэффициент детерминации (т.е. доля, которую дисперсия остатков составляет от обшей дисперсии в данных). Остальные две метрики рассчитываются с использованием т.н. “ошибок следующего шага” (one-step-ahead errors), которые вычисляются в ходе подгонки модели как \(y_t - E(y_t|Y_{t-1}, \theta)\), где \(Y_{t-1} = y_1, y_2, \dots y_{t-1}\), а \(\theta\) — вектор с текущими оценками параметров модели. При необходимости эти ошибки можно извлечь с помощью функции bsts.prediction.errors(), подав на нее соответствующий модельный объект. Возвращаемая методом summary() метрика prediction.sd представляет собой стандартное отклонение ошибок следующего шага, рассчитанных по обучающим данным, а relative.gof — это т.н. статистика Харви (Harvey’s goodness of fit statistic). Статистика Харви похожа на коэффициент детерминации и вычисляется как \(R_D^2 = 1 - \sum \nu^2 /(n-2) \times \text{var}(\text{diff}(y))\), где \(\nu\) — ошибки следующего шага, \(n\) — число наблюдений \(y\) в анализируемом временном ряду, а \(\text{var}\) и \(\text{diff}\) — функции для расчета дисперсии и перехода к разностям (дифференцированию) временного ряда соответственно.
Качество bsts–моделей можно проанализировать также графически с помощью диаграмм нескольких типов. Так, стандартный метод plot() изображает обучающие данные и оцененное на их основе апостериорное совместное распределение компонент модели в каждый момент времени (\(Z_t^\intercal \alpha_t\); см. рис. 7.4 и разд. 7.1):
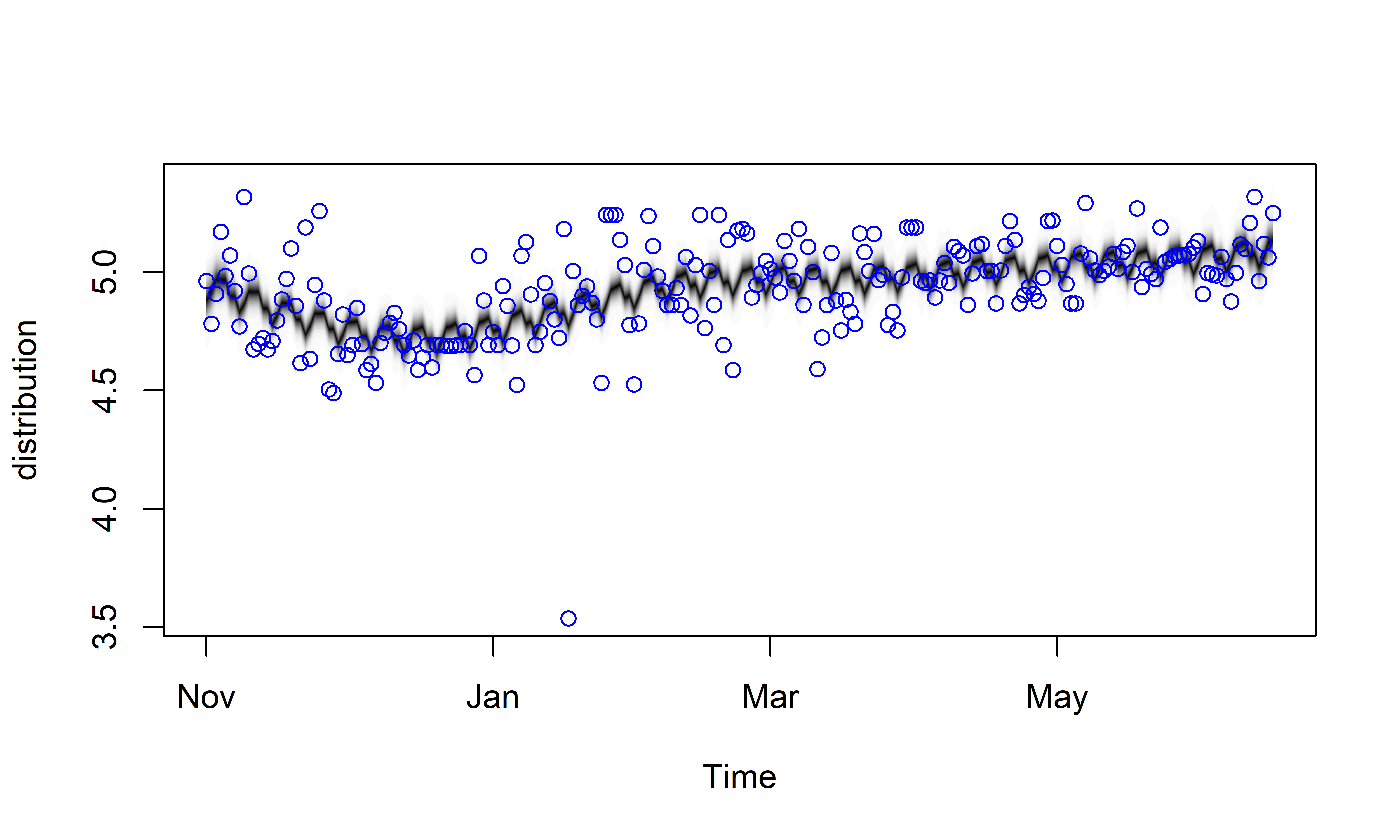
РИСУНОК 7.4: Результат подгонки модели M19. Кружками показаны обучающие данные. Полупрозрачными черными точками показано апостериорное совместное распределение компонент модели. Области плотного расположения этих точек выглядят темнее и соответствуют областям с большей апостериорной вероятностью. На каждую временную отметку приходится niter = 1500 таких точек
Метод plot() в сочетании с аргументом y = "components" позволяет также изобразить вклад отдельных компонент модели (рис. 7.5; этот метод принимает и ряд других аргументов — см. справочный файл, доступный по команде ?plot.bsts):
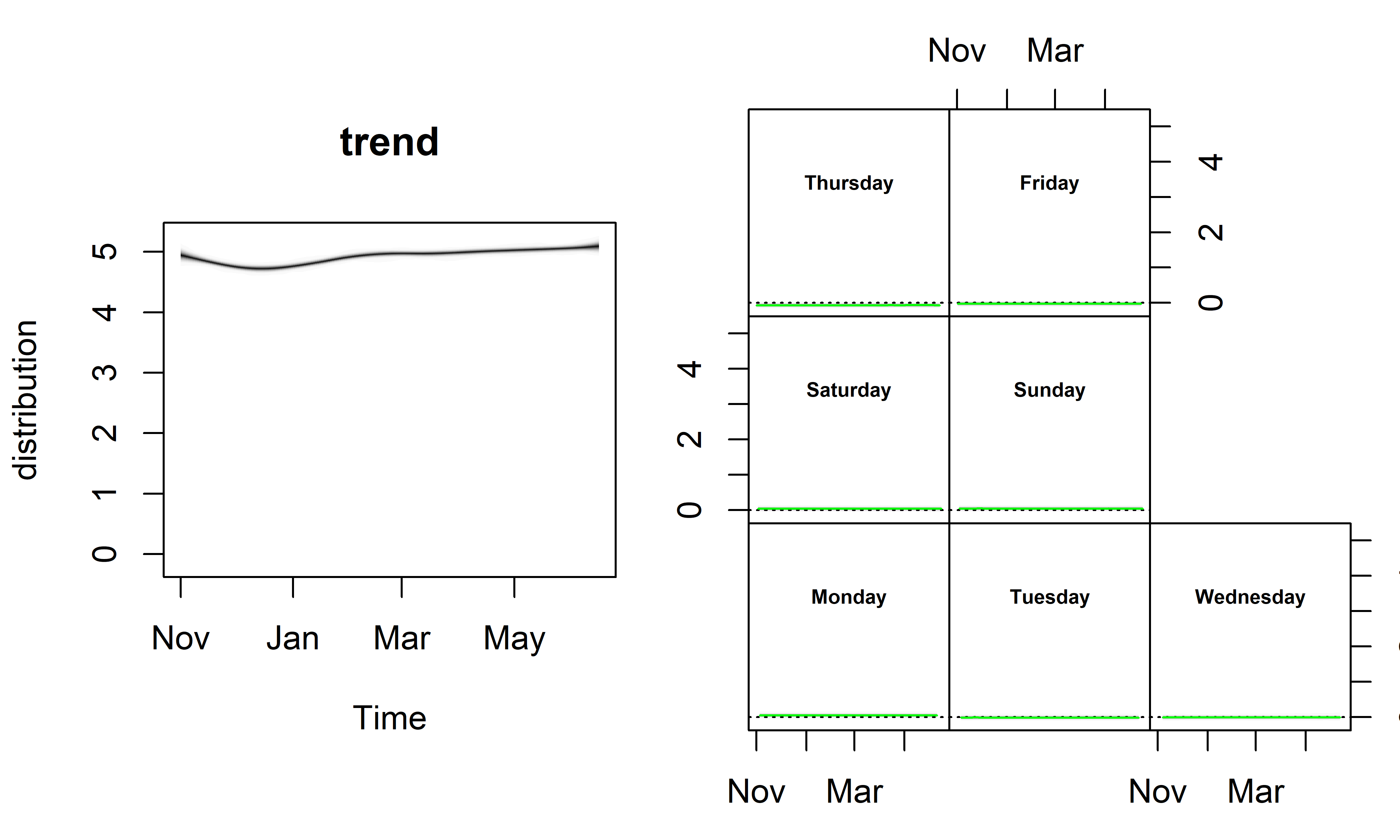
РИСУНОК 7.5: Апостериорные распределения компонент модели M19. Слева: локальный линейный тренд. Справа: эффекты дней недели
Поскольку все графики на рис. 7.5 имеют одинаковые оси ординат, то эффекты дней недели рассмотреть очень сложно. Мы можем изобразить их отдельно с помощью следующей команды (рис. 7.6):
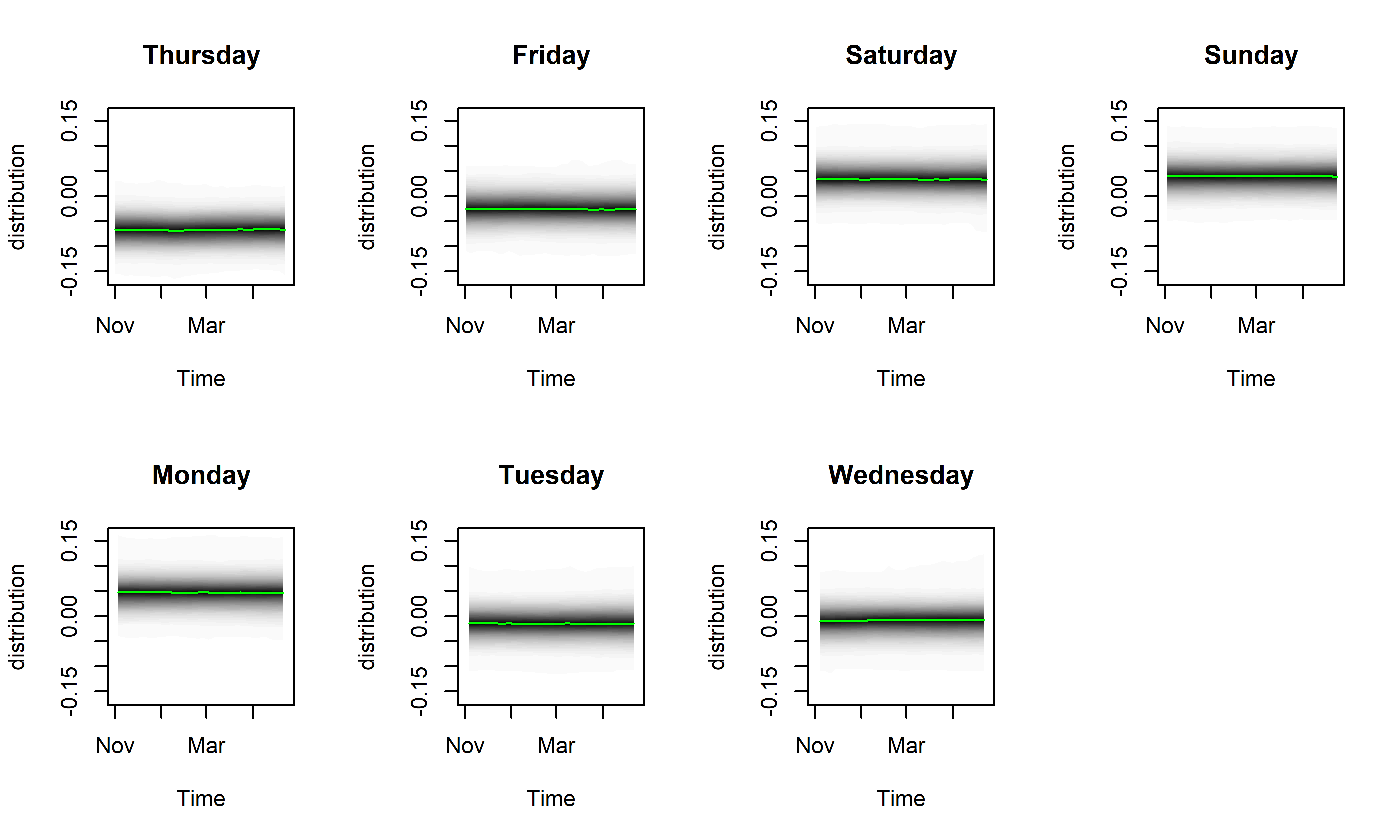
РИСУНОК 7.6: Апостериорные распределения эффектов дней недели, оцененные с помощью модели M19. Зеленые линии соответствуют медианам этих распределений
На рис. 7.6 лучше видно, что цена на номер в гостинице 73738 в среднем была несколько выше в субботу (Saturday), воскресенье (Sunday) и понедельник (Monday), чем в другие дни, и что эффекты каждого из дней недели были практически постоянны на протяжении всего исторического периода. Тем не менее вклад сезонной компоненты в целом оказался весьма незначительным, по сравнению с вкладом линейного тренда, что согласуется также с результатом разведочного анализа этих данных, выполненного в гл. 4.
Важным свойством хорошей модели временного ряда является отсутствие автокорреляции в ее остатках. Для визуальной проверки этого служит команда AcfDist(), которая принимает матрицу с остатками модели и строит диаграммы размахов (“ящики с усами”) для апостериорных распределений автокорреляционной функции. В идеале центры этих апостериорных распределений (начиная со сдвига 1 и далее) должны приходится на 0, однако в случае с моделью M19 это явно не так (рис. 7.7): хорошо видна цикличность с периодом, составляющим примерно 7 временных шагов. Похожее свойство этих данных мы ранее обнаружили также в ходе их разведочного анализа (гл. 4).
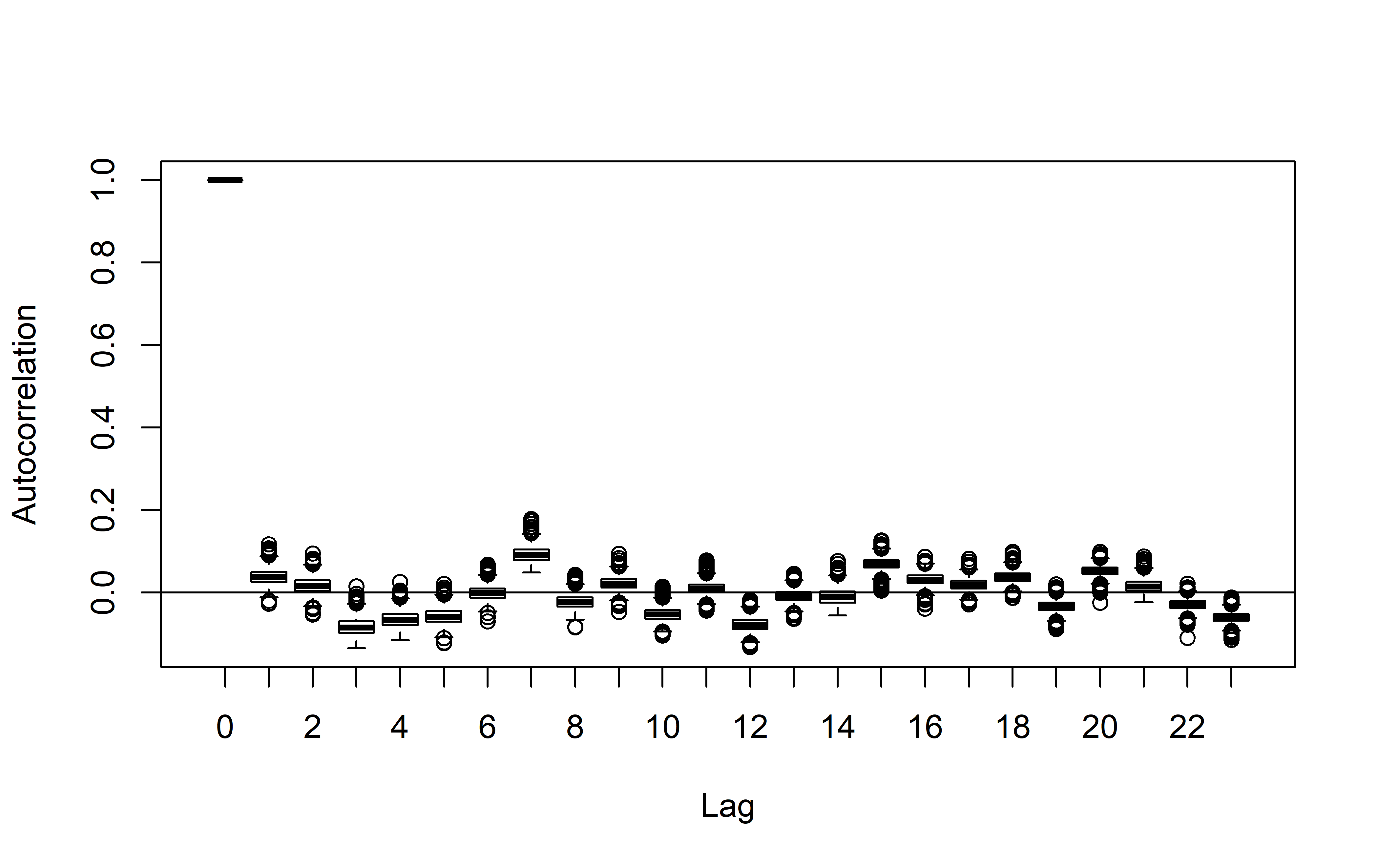
РИСУНОК 7.7: Апостериорные распределения автокорреляционной функции остатков модели M19
Попробуем улучшить модель M19, добавив в нее авторегрессионный процесс и одновременно исключив сезонную компоненту. Обратите внимание на то, что для добавления авторегрессионной компоненты в приведенном ниже коде использована функция AddAutoAr(), которая, в отличие от AddAr(), применяет метод “spike–and–slab” для регуляризации авторегрессионных коэффициентов: пользователь задает максимально возможное количество таких коэффициентов (с помощью аргумента lag), но некоторые из них в отдельных MCMC–итерациях окажутся в точности приравнены к нулю.
ss <- list()
ss <- AddLocalLinearTrend(ss, y_73738)
ss <- AddAutoAr(ss, y_73738, lag = 7)
M20 <- bsts(y_73738, ss,
timestamps = dt_73738,
niter = 1500, ping = 0, seed = 42)
summary(M20)## $residual.sd
## [1] 0.09866681
##
## $prediction.sd
## [1] 0.1874644
##
## $rsquare
## [1] 0.7794775
##
## $relative.gof
## [1] 0.3970419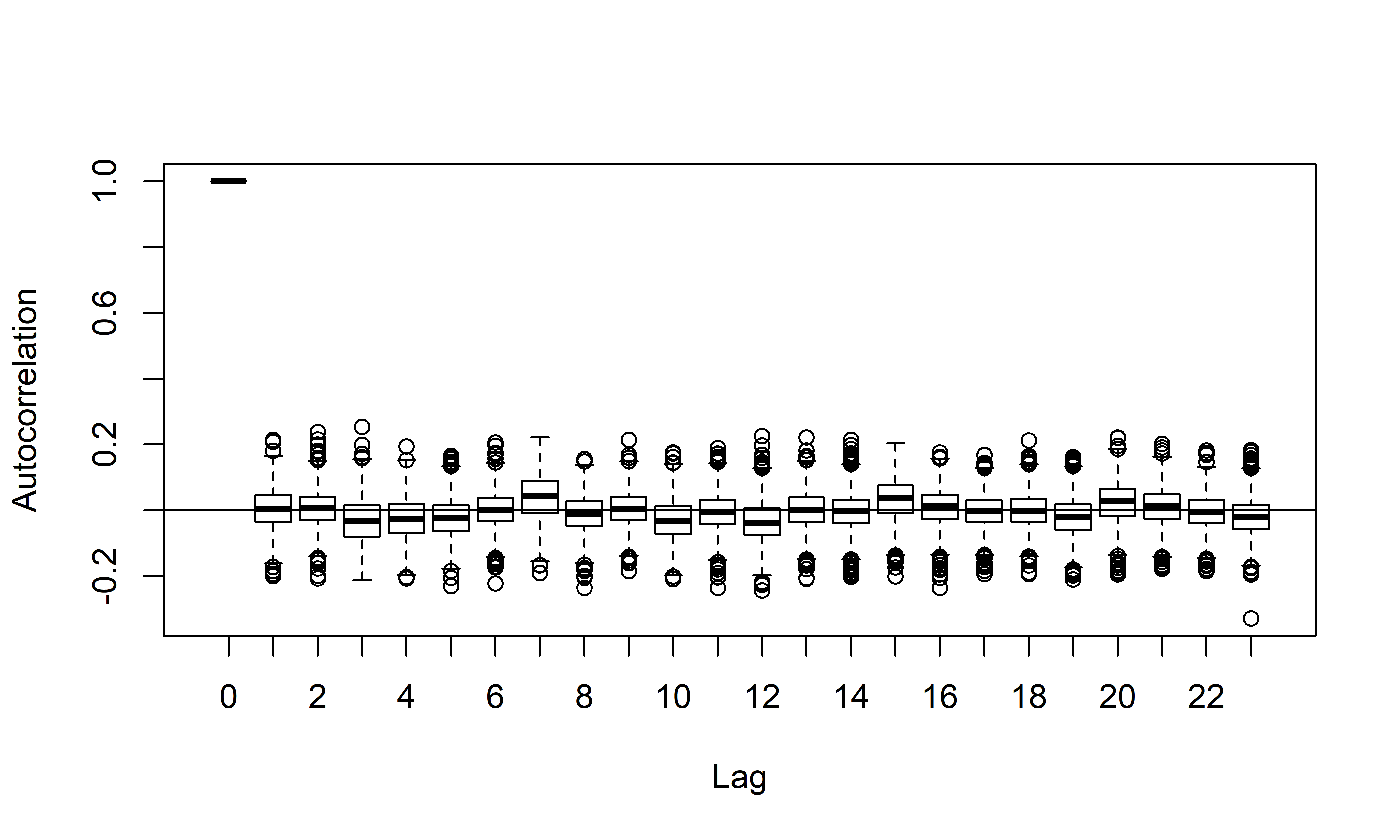
РИСУНОК 7.8: Апостериорные распределения автокорреляционной функции остатков модели M20
Как следует из приведенных выше диагностических метрик и из рис. 7.8, модель M20 гораздо лучше описывает обучающие данные, чем модель M19. Это видно также на рис. 7.9, где изображены обучающие данные и апостериорное совместное распределение компонент M20, и на рис. 7.10, изображающем апостериорные распределения отдельных компонент этой модели:
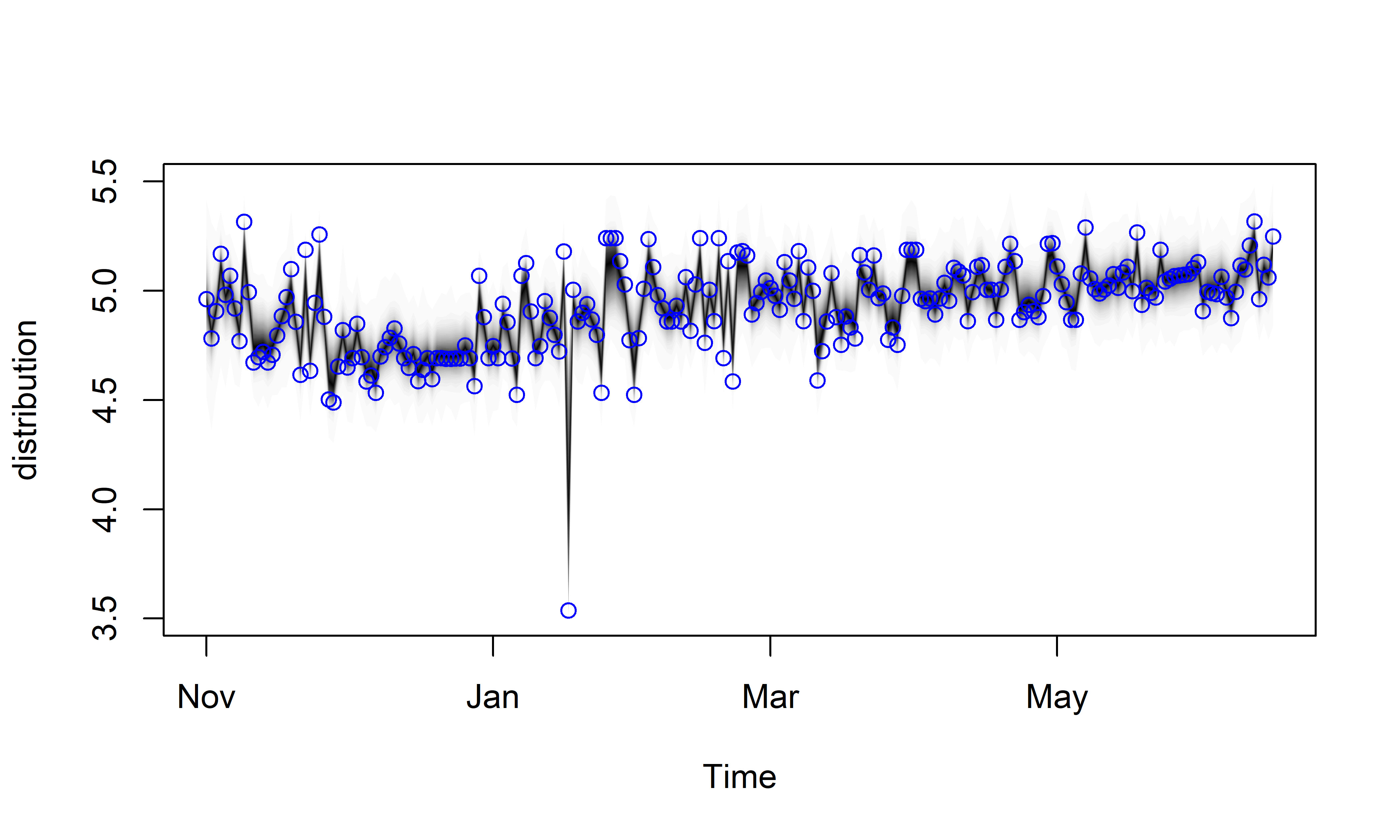
РИСУНОК 7.9: Результат подгонки модели M20
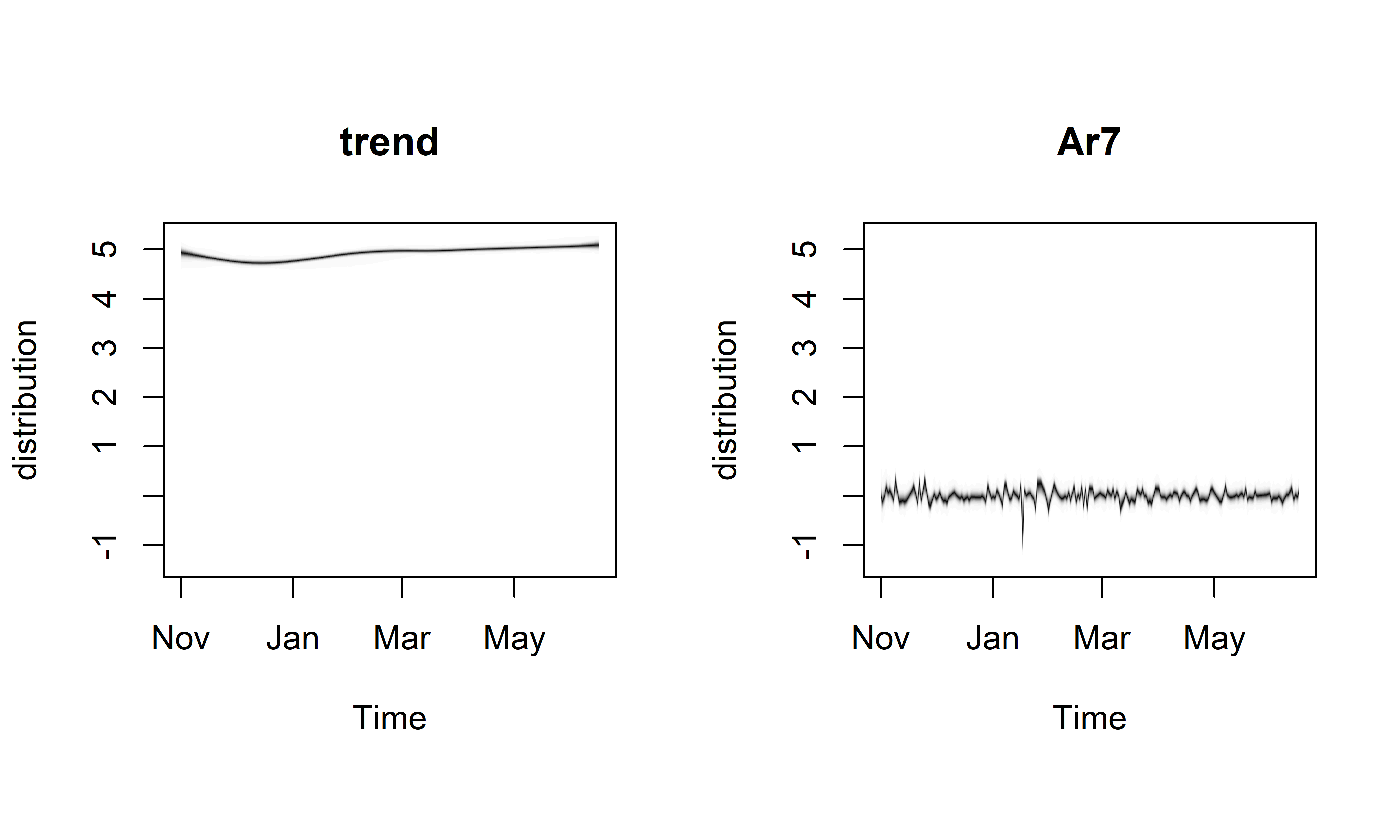
РИСУНОК 7.10: Апостериорные распределения компонент модели M20. Слева: локальный линейный тренд. Справа: авторегрессионная компонента
Качество нескольких bsts-моделей можно одновременно проанализировать с помощью функции CompareBstsModels(), которая изображает накопленные средние абсолютные ошибки следующего шага для каждой из сравниваемых моделей. Под графиком таких кривых накопленных ошибок изображаются также исходные обучающие данные, что позволяет лучше понять, где именно та или иная модель плохо справляется с описанием данных. На рис. 7.11 кривая накопленных ошибок модели M20 проходит ниже кривой M19, что еще раз подтверждает более высокое качество модели M20.
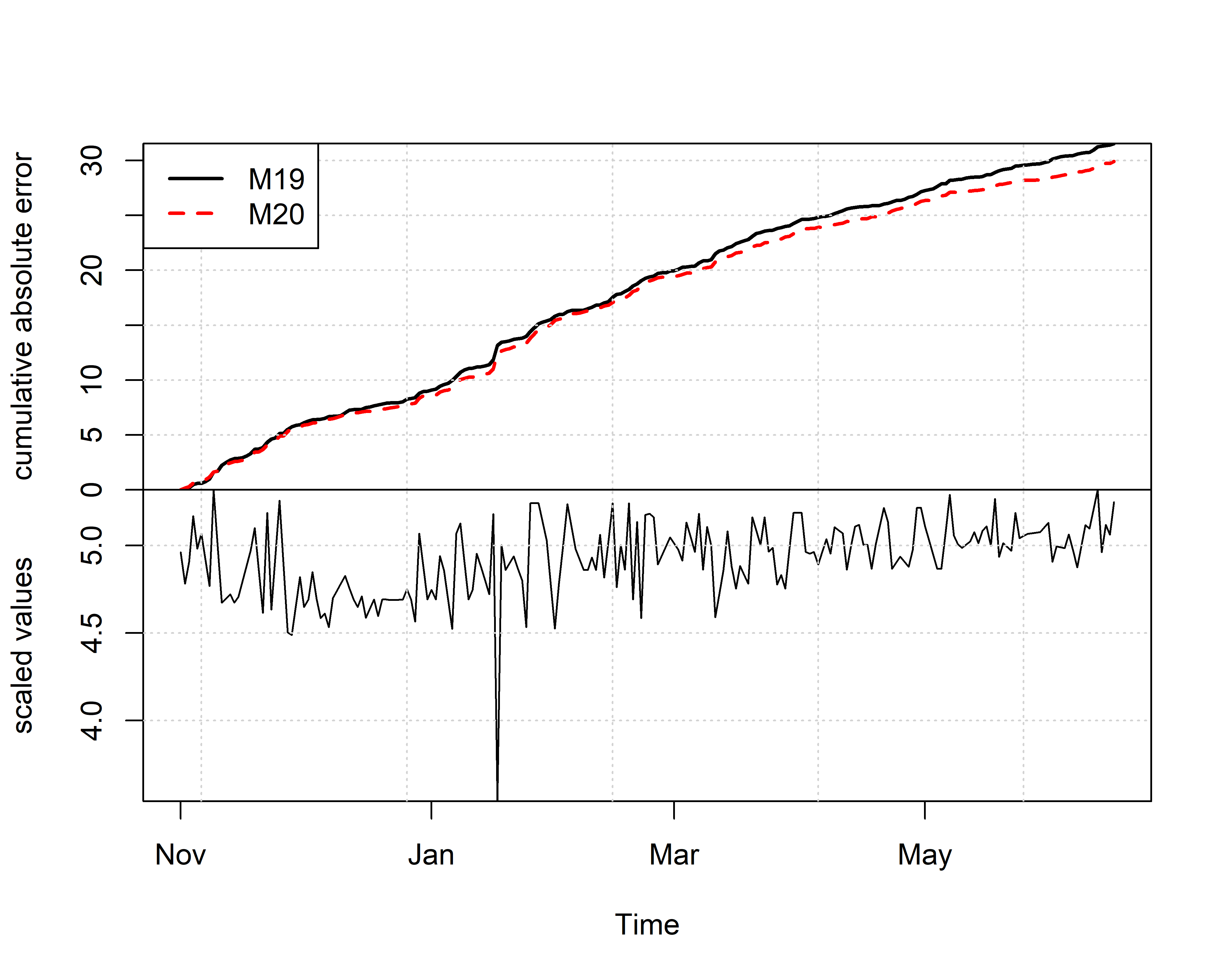
РИСУНОК 7.11: Пример сравнения качества двух моделей (M19 и M20) с помощью ошибок следующего шага. Вверху: накопленные средние абсолютные ошибки следующего шага. Внизу: обучающие данные
7.5 Модели с предикторами
Как было отмечено в разд. 7.1, помимо стандартных компонент тренда и сезонности в структурные модели временных рядов можно включить также эффекты предикторов. Для этого необходимо воспользоваться аргументом formula функции bsts() и указать обычным для R образом имена соответствующих переменных справа от значка тильды (например, y ~ x1 + x2 + x3, где x1, x2 и x3 — это имена предикторов). Все предикторы должны содержаться в одной таблице данных, которая подается на функцию bsts() с помощью аргумента data.
Воспользуемся в качестве предикторов стоимостью номеров в двух других гостиницах (с идентификаторами 13252 и 83045) из набора данных hotels. Хотя зависимой переменной в bsts–моделях разрешается иметь пропущенные значения, наличие пропусков в предикторах недопустимо. Мы уже сталкивались с аналогичным требованием при построении prophet–моделей (разд. 6.7), где пропущенные наблюдения в предикторах были восстановлены с помощью метода LOCF (подразд. 1.5.3). Здесь мы воспользуемся другим подходом и восстановим пропущенные значения на основе отдельных bsts–моделей, подогнанных к данным по стоимости номеров в соответствующих гостиницах. Такой подход часто дает реалистичные оценки пропущенных наблюдений, что является одним из больших преимуществ байесовских методов анализа временных рядов.
В приведенном ниже коде происходит подготовка каждого временного ряда предиктора к моделированию и подгонка соответствующих моделей, структура которых идентична таковой у модели M20:
# Подготовка данных:
h <- hotels %>%
filter(prop_id != 73738) %>%
group_by_key(prop_id) %>%
index_by(dt = as.Date(date_time)) %>%
summarise(y = mean(log(price_usd))) %>%
tsibble::fill_gaps() %>%
filter(as.Date(dt) <= cut_point)
# Модель для гостиницы `13252`
y_13252 <- h %>% filter(prop_id == 13252) %>% pull(y)
dt_13252 <- h %>% filter(prop_id == 13252) %>% pull(dt)
ss <- list()
ss <- AddLocalLinearTrend(ss, y_13252)
ss <- AddAutoAr(ss, y_13252, lag = 7)
M13252 <- bsts(y_13252, ss,
timestamps = dt_13252,
niter = 1500, ping = 0, seed = 42)
# Модель для гостиницы `83045`
y_83045 <- h %>% filter(prop_id == 83045) %>% pull(y)
dt_83045 <- h %>% filter(prop_id == 83045) %>% pull(dt)
ss <- list()
ss <- AddLocalLinearTrend(ss, y_83045)
ss <- AddAutoAr(ss, y_83045, lag = 7)
M83045 <- bsts(y_83045, ss,
timestamps = dt_83045,
niter = 1500, ping = 0, seed = 42)Результаты подгонки обеих моделей приведены на рис. 7.12.
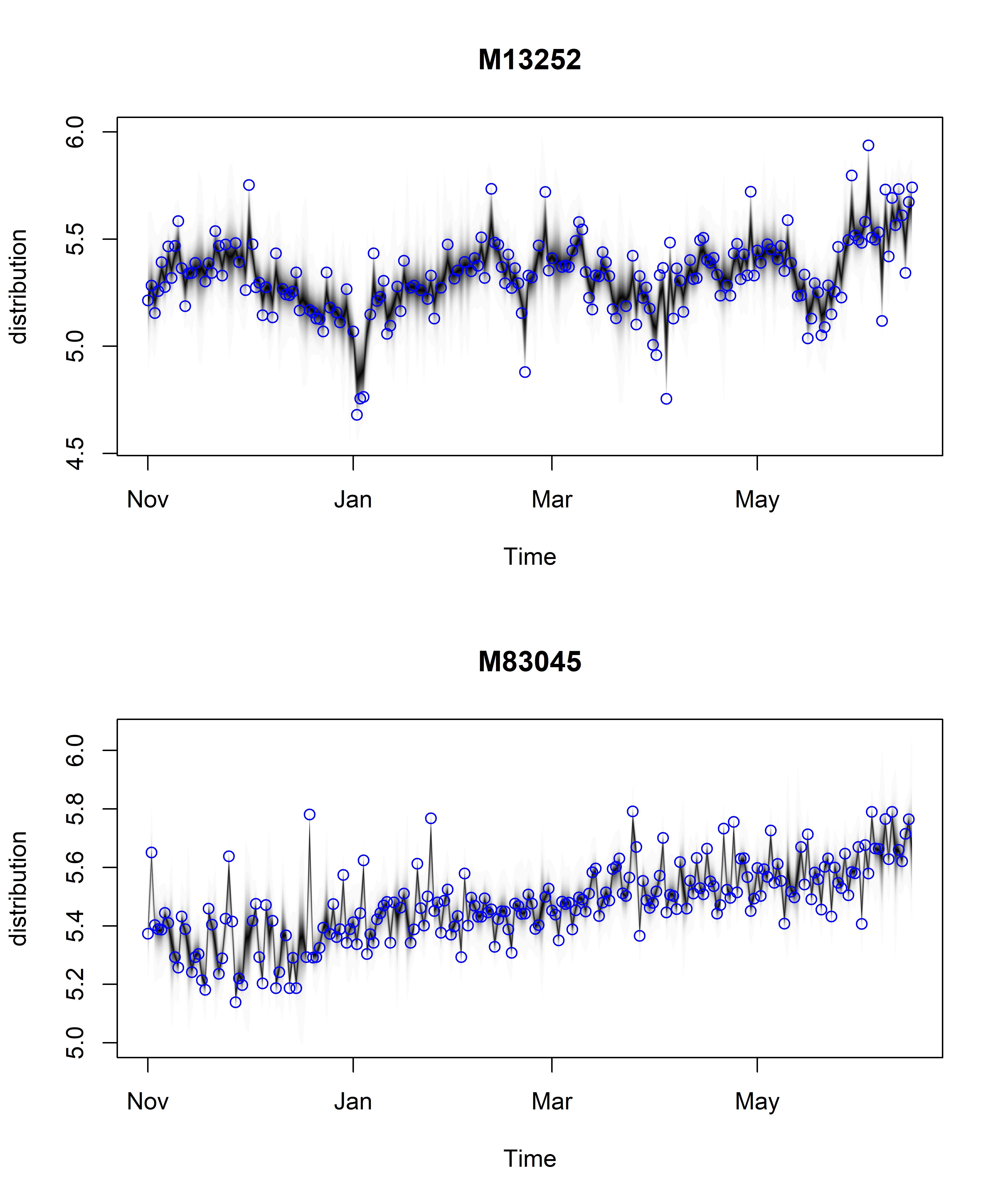
РИСУНОК 7.12: Результаты подгонки моделей по данным стоимости номеров в гостиницах 13252 и 83045
В пакете bsts нет готовой функции, позволяющей извлекать предсказанные значения для обучающих данных (подобно базовой функции fitted()). Но не беда — мы можем легко рассчитать эти значения самостоятельно по результатам MCMC-симуляций вклада каждой компоненты модели. Эти результаты хранятся в слоте state.contributions модельного объекта в виде массива размерностью \(i \times s \times l\), где \(i\) — количество итераций MCMC, \(s\) — число входящих в модель компонент, а \(l\) — длина временного ряда (включая пропущенные значения). В рассматриваемом нами примере \(i = 1500\), \(s = 2\), а \(l = 228\):
## [1] 1500 2 228## [1] 1500 2 228Для расчета модельного значения стоимости гостиничного номера на определенной временной отметке необходимо суммировать вклады всех компонент модели, соответствующих этой отметке. Для каждой временной отметки мы в итоге получим 1500 оценок стоимости гостиничного номера. Наиболее вероятную оценку можно было бы далее рассчитать путем простого усреднения этих 1500 значений. Однако, как это обычно бывает при выполнении MCMC-симуляций, первые несколько итераций алгоритма во время его “разогрева” (“burn–in”) дают неустойчивые оценки моделируемой величины. В связи с этим принято такие начальные итерации исключать из анализа. Функция SuggestBurn() из пакета bsts вычисляет количество итераций MCMC, которые следует отбросить:
# Аргумент `proportion` задает число последних MCMC-итераций
# (в виде доли от общего количества итераций), которые
# используются для нахождения периода "разогрева" алгоритма
(burn_13252 <- SuggestBurn(proportion = 0.1, M13252))## [1] 78## [1] 112Рассчитаем предсказанные моделями M13252 и M83045 наиболее вероятные значения стоимости гостиничных номеров, отбросив первые 78 и 112 МСМС–оценок соответственно, и изобразим результаты на графиках (рис. 7.13):
fitted_M13252 <- M13252$state.contributions %>%
apply(., MARGIN = 3, FUN = rowSums) %>%
.[-(1:burn_13252), ] %>%
colMeans()
fitted_M83045 <- M83045$state.contributions %>%
apply(., MARGIN = 3, FUN = rowSums) %>%
.[-(1:burn_83045), ] %>%
colMeans()
par(mfrow = c(2, 1))
plot(fitted_M13252, main = "M13252", type = "l", ylim = c(4.6, 6.4))
points(h %>% filter(prop_id == 13252) %>% pull(y), col = "blue")
plot(fitted_M83045, main = "M83045", type = "l", ylim = c(4.6, 6.4))
points(h %>% filter(prop_id == 83045) %>% pull(y), col = "blue")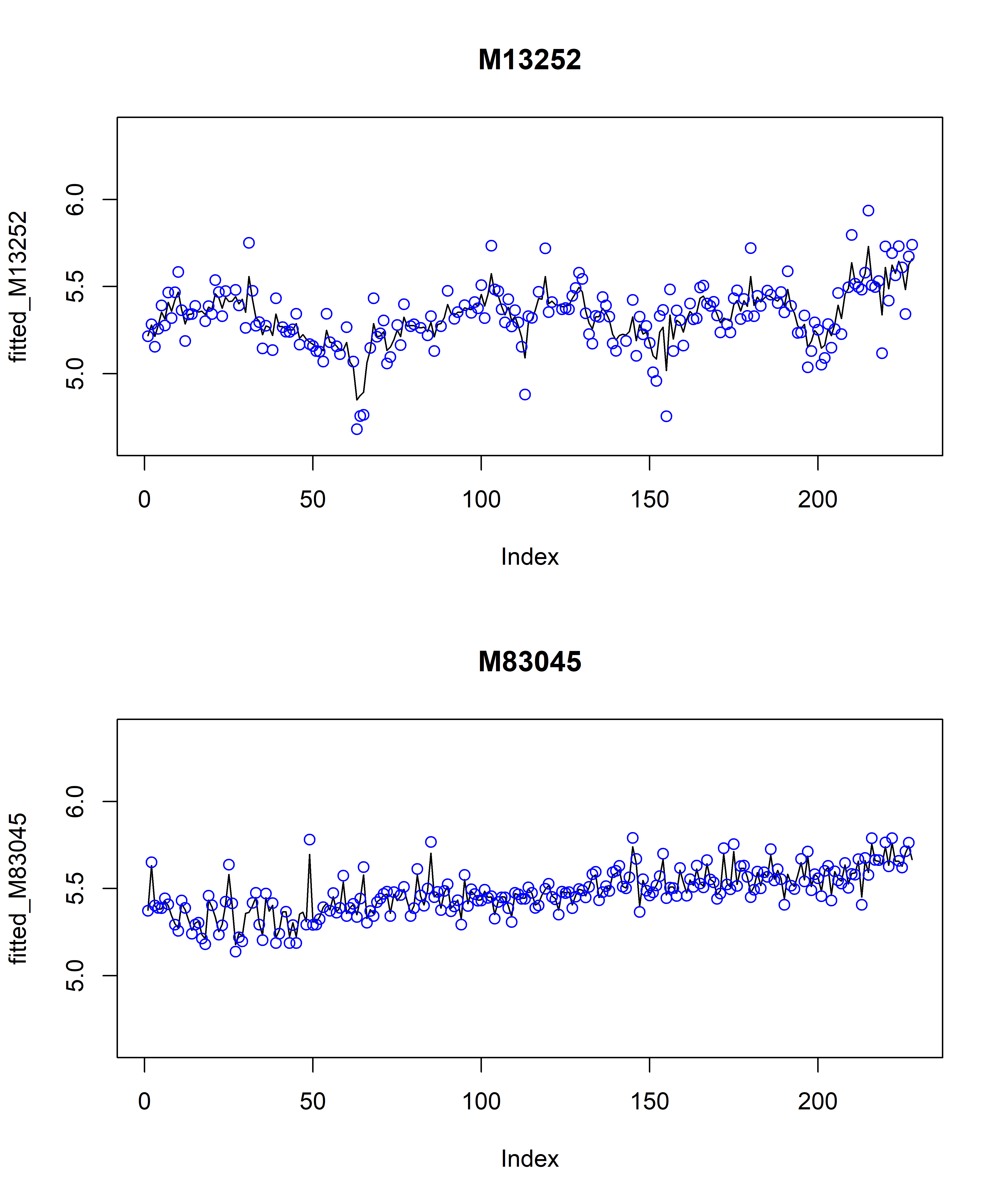
РИСУНОК 7.13: Модельные значения (сплошные линии) и обучающие данные по стоимости номеров в гостиницах 13252 и 83045 (кружки)
Заменим теперь пропущенные данные по стоимости номеров в гостиницах 13252 и 83045 их модельными значениями (см. столбец y_imputed):
require(tidyr)
predictors <- bind_rows(tibble(prop_id = 13252,
dt = dt_13252,
y_fitted = fitted_M13252),
tibble(prop_id = 83045,
dt = dt_83045,
y_fitted = fitted_M83045)) %>%
inner_join(., h, by = c("prop_id", "dt")) %>%
mutate(y_imputed = ifelse(is.na(y), y_fitted, y),
prop_id = paste0("y_", prop_id)) %>%
dplyr::select(-y, -y_fitted) %>%
pivot_wider(names_from = prop_id, values_from = y_imputed)
predictors## # A tibble: 228 x 3
## dt y_13252 y_83045
## <date> <dbl> <dbl>
## 1 2012-11-01 5.21 5.37
## 2 2012-11-02 5.28 5.65
## 3 2012-11-03 5.16 5.40
## 4 2012-11-04 5.26 5.39
## 5 2012-11-05 5.39 5.39
## 6 2012-11-06 5.28 5.44
## 7 2012-11-07 5.47 5.41
## 8 2012-11-08 5.32 5.34
## 9 2012-11-09 5.47 5.29
## 10 2012-11-10 5.58 5.26
## # ... with 218 more rowsВ моделируемом нами временном ряду стоимости номеров в гостинице 73738 есть одно аномально низкое значение, приходящееся на временную отметку 2013-01-17 (рис. 7.3). Причина появления этого аномального наблюдения, к сожалению, не известна. Хотя модель M20 ранее вполне успешно “справилась” с этим наблюдением без каких–либо специальных действий с нашей стороны (рис. 7.9), мы могли бы также представить его в явном виде с помощью индикаторной переменной, которая принимает значение 1 на отметке 2013-01-17 и 0 на всех остальных отметках. Добавим такую индикаторную переменную в таблицу predictors:
anomaly_dt <- h73738_train %>%
filter(y == min(y, na.rm = TRUE)) %>%
pull(dt)
predictors <- predictors %>%
mutate(anomaly_event = ifelse(dt == anomaly_dt, 1, 0))Построим теперь новую модель стоимости номеров в гостинице 73738, в которую помимо использованных нами ранее компонент войдут также независимые переменные из таблицы predictors:
# Добавление предикторов в таблицу с исходными данными:
h73738_train <- h73738_train %>%
left_join(predictors, ., by = "dt")
ss <- list()
ss <- AddLocalLinearTrend(ss, y_73738)
ss <- AddAutoAr(ss, y_73738, lag = 7)
M21 <- bsts(y ~ y_13252 + y_83045 + anomaly_event, ss,
data = h73738_train,
timestamps = dt_73738,
niter = 1500, seed = 42, ping = 0)
print(summary(M21), digits = 3)## $residual.sd
## [1] 0.0529
##
## $prediction.sd
## [1] 0.16
##
## $rsquare
## [1] 0.937
##
## $relative.gof
## [1] 0.562
##
## $size
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.00 1.00 1.00 1.04 1.00 3.00
##
## $coefficients
## mean sd mean.inc sd.inc inc.prob
## anomaly_event -1.44e+00 0.14375 -1.43979 0.1438 1.0000
## y_13252 2.82e-04 0.00394 0.01500 0.0250 0.0188
## y_83045 8.82e-05 0.00379 0.00504 0.0288 0.0175
## (Intercept) 0.00e+00 0.00000 0.00000 0.0000 0.0000Приведенная сводка по модели M21 несколько отличается от виденных нами ранее. В одном из новых элементов сводки — size — приведена таблица с описательными статистиками по количеству предикторов, включенных в модель на разных итерациях алгоритма МСМС. Как было отмечено выше (разд. 7.1), в ходе подгонки модели выполняется регуляризация ее размера с помощью метода “spike–and–slab”, в результате чего не все предикторы входят во все МСМС–реализации. В нашем примере видно, что в большинстве случаев в модель был включен лишь один предиктор (см. медианное значение).
Другой новый элемент в сводке — coefficients — содержит описательные статистики по оцененным коэффициентам каждого из предикторов. Особенно важным показателем здесь является т.н. апостериорная вероятность включения предиктора в модель (posterior inclusion probability, см. столбец inc.prob). Как следует из названия, это вероятность использования того или иного предиктора в отдельных MCMC–реализациях модели, в т.ч. при расчете прогнозных значений (см. ниже). Хорошо видно, что наиболее важным предиктором оказалась индикаторная переменная anomaly_event, тогда как переменные y_13252 и y_83045 имеют достаточно низкую вероятность быть включенными в модель. Апостериорные вероятности включения предикторов можно также изобразить графически при помощи следующей простой команды (рис. 7.14):
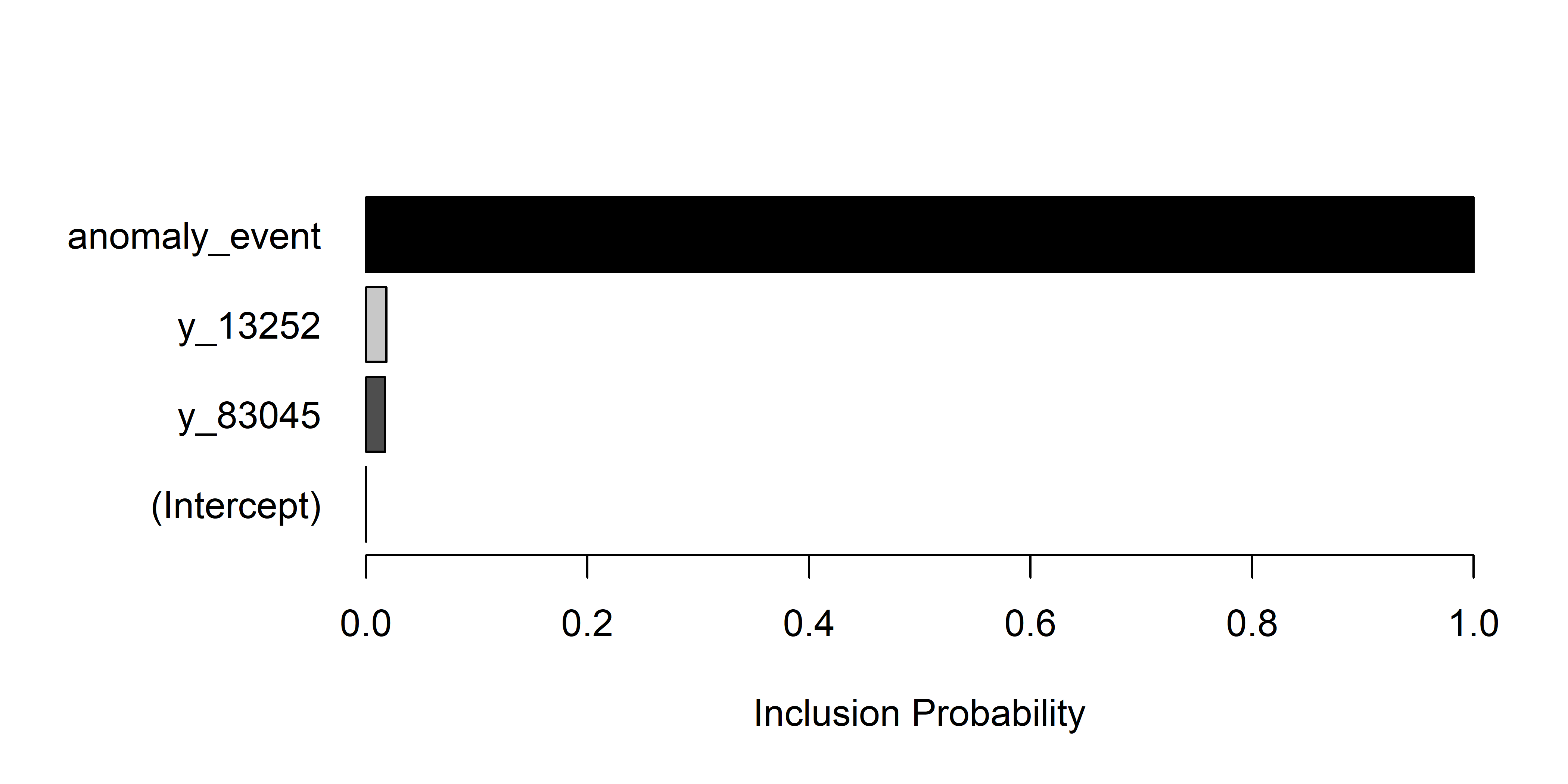
РИСУНОК 7.14: Апостериорные вероятности включения трех предикторов в модель M21. Чем темнее заштриховка столбца, тем более вероятно, что соответствующая переменная отрицательно коррелирует с зависимой переменной. (Intercept) обозначает свободный член регрессионного уравнения
7.6 Выбор оптимальной модели
До сих пор мы оценивали адекватность bsts–моделей по тому, насколько хорошо они описывали обучающие данные. Безусловно, такой подход сопровождается высоким риском выбрать в качестве оптимальной переобученную модель. Диагностика с использованием ошибок следующего шага (разд. 7.4; см. также справочный файл по функции bsts.prediction.errors()) лишь отчасти помогает застраховаться от этого, и единственным объективным тестом качества модели всегда будет точность ее предсказаний на независимом наборе данных.
Объекты класса bsts обладают стандартным методом predict(), основными аргументами которого являются следующие (подробнее см. справочный файл, доступный по команде ?predict.bsts):
object— модельный объект;horizon— целое число, задающее длину прогнозного горизонта;newdata— вектор, матрица или таблица со значениями предикторов (если таковые имеются);timestamps— вектор с временными отметками, соответствующими строкам вnewdata, для которых необходимо рассчитать прогнозные значения;plot.original— количество последних наблюдений из обучающих данных, которые необходимо изобразить на графике;na.action— функция, которую следует применить к пропущенным значениям вnewdata;quantiles— вектор с двумя значениями, задающими нижний и верхний лимиты доверительного интервала прогнозных значений (по умолчаниюс(0.025, 0.975), что соответствует 95%–ному интервалу);seed— зерно генератора случайных чисел, которое можно указать для воспроизводимости результатов.
Полученные с помощью метода predict() прогнозные значения можно также визуализировать с помощью метода plot() (рис. 7.15 и 7.16):
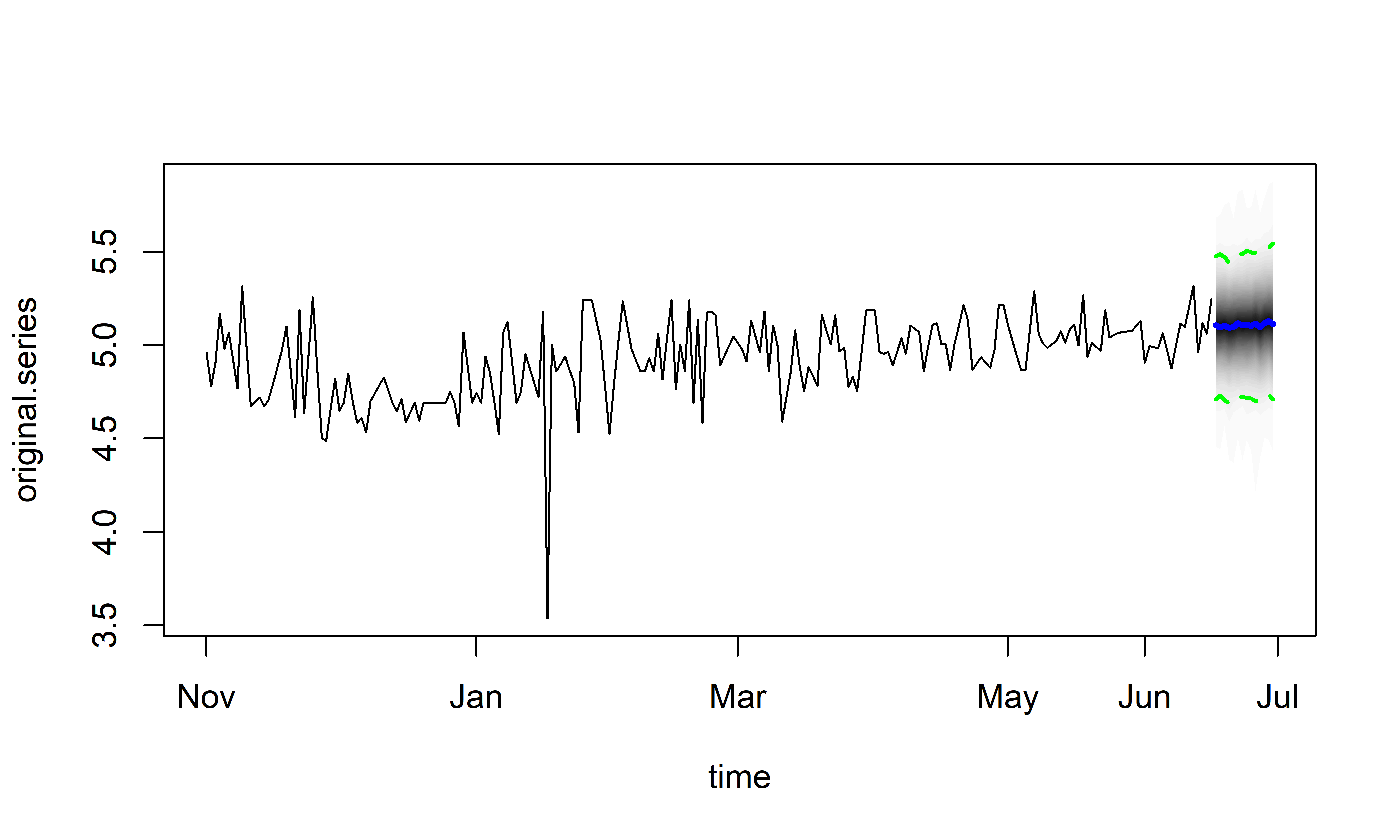
РИСУНОК 7.15: Обучающие данные (черная линия) и прогнозные значения, полученные с помощью модели M20. Синей линией показаны наиболее вероятные будущие значения временного ряда. Вокруг этой линии полупрозрачными черными точками показаны также другие возможные реализации будущих значений. Зеленые прерывистые линии ограничивают 95%–ный доверительный интервал предсказанных значений
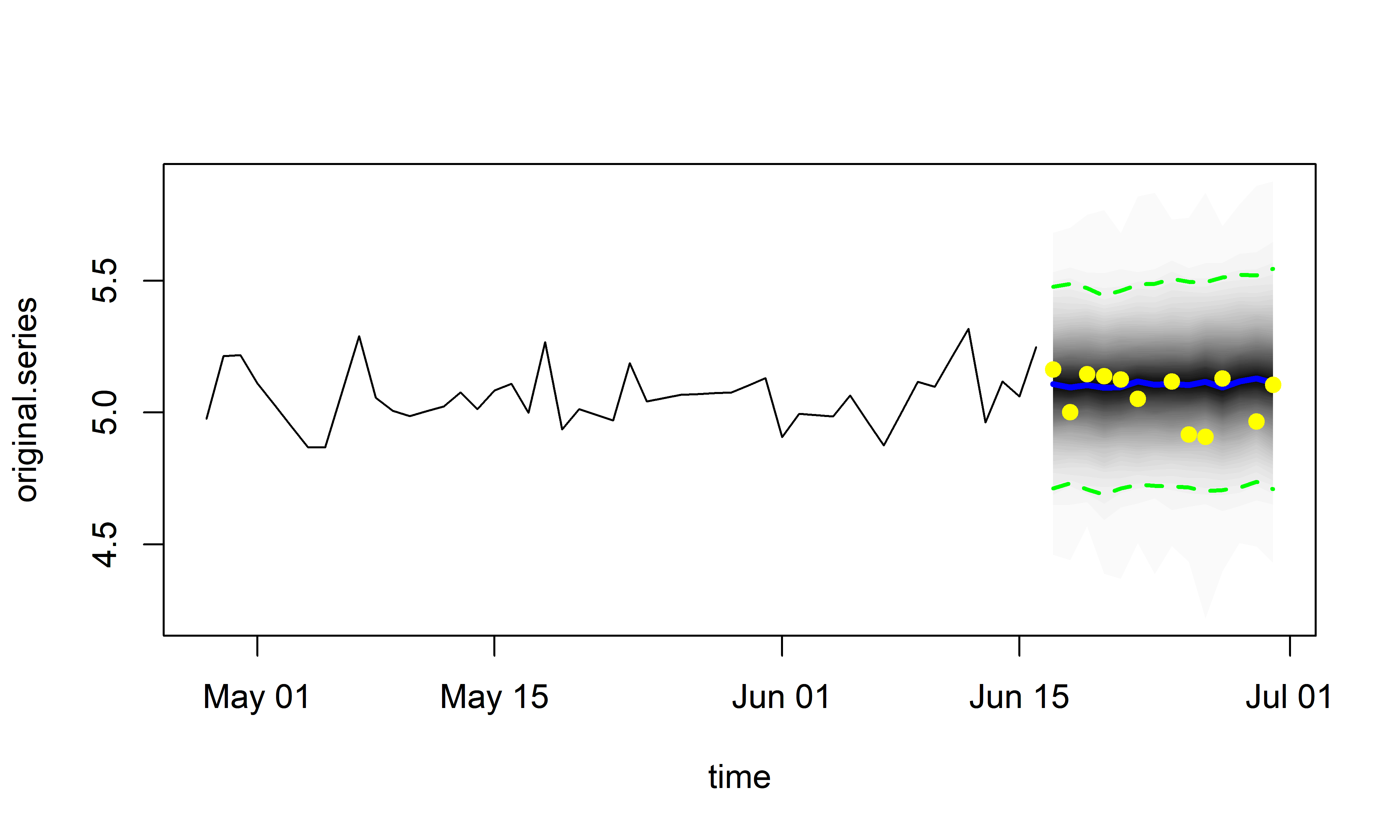
РИСУНОК 7.16: То же, что на рис. 7.15, но с изображением только последних 50 наблюдений из обучающих данных. Желтыми точками показаны также наблюденные данные из проверочной выборки, что позволяет визуально оценить качество прогноза
Рассчитаем теперь прогнозные значения для всех трех простроенных нами моделей и сравним эти предсказания с данными из проверочной выборки, которые хранятся в таблице h73738_test (разд. 7.4). В качестве метрики для выбора оптимальной модели применим cреднюю абсолютную удельную ошибку предсказаний (MAPE; подразд. 6.8.3). Поскольку bsts–модели предсказывают большое количество возможных реализаций будущих значений зависимой переменной, то для расчета MAPE мы воспользуемся медианными значениями этих возможных реализаций. Метод predict() автоматически вычисляет такие значения и сохраняет их в элементе median возвращаемого списка:
# Функция для расчета средней абсолютной удельной ошибки:
mape <- function(observed, predicted){
na_ind <- which(is.na(observed))
observed <- na.omit(observed)
predicted <- predicted[-na_ind]
mean(abs(observed - predicted)/observed)
}
# Предсказания модели M19:
M19_pred <- predict(M19, horizon = 14) %>% .$median
# Предсказания модели M20:
M20_pred <- M20_pred$median
# Для получения предсказаний с помощью модели M21
# нам сначала необходимо создать таблицу с будущими
# значениями всех входящих в нее предикторов:
predictors_future <- tibble(
dt = h73738_test$dt,
y_13252 = predict(M13252, horizon = 14) %>% .$median,
y_83045 = predict(M83045, horizon = 14) %>% .$median,
anomaly_event = 0
)
M21_pred <- predict(M21, horizon = 14,
newdata = predictors_future) %>% .$median
# MAPE для всех трех моделей:
sapply(list("M19" = M19_pred,
"M20" = M20_pred,
"M21" = M21_pred),
mape, observed = h73738_test$y) %>%
round(., 4)## M19 M20 M21
## 0.0194 0.0157 0.0163Как следует из приведенных результатов, оптимальной следует считать модель M20. Интересно, что модель M21, несмотря на наличие в ней дополнительных предикторов, оказалась на втором месте по качеству прогноза. Подобная ситуация, когда включение предикторов не сопровождается улучшением качества модели временного ряда, довольно обычна и может быть обусловлена многими факторами (слабая связь между предикторами и моделируемой переменной, ошибки, возникающие при расчете прогнозных значений самих предикторов, эффект переобучения и т.п.).
Возможности пакета bsts для прогнозирования временных рядов намного шире описанных в этой вводной главе. Дополнительную информацию о пакете и примеры его использования можно найти в статье Scott (2017), а также на сайте Стивена Скотта.