ГЛАВА 5 Извлечение признаков с помощью пакета feasts

Подобно свойствам другим совокупностей, мы можем компактно охарактеризовать свойства временных рядов с помощью стандартных показателей описательной статистики (среднее значение, медиана, дисперсия, стандартное отклонение, квантили и т.п.). Поскольку наблюдения во временных рядах упорядочены, то для них можно рассчитать также и многие специфичные показатели, такие как автокорреляция (гл. 4), выраженность тренда и сезонной компоненты, стационарность ряда и т.п.

Помимо того, что описательные статистики временных рядов представляют интерес сами по себе, их используют также в качестве признаков, или предикторов, при создании предсказательных моделей и в других задачах, решаемых с помощью методов машинного обучения (кластеризация, выявление аномалий и т.п.). Извлечение таких признаков из временных рядов с помощью R не составляет труда — для этого вполне подойдут как базовые функции, так и функции из многочисленных дополнительных пакетов. Однако учитывая то, как часто возникает необходимость в подобных вычислениях, в идеале было бы удобно иметь один–два пакета, в которых реализован соответствующий функционал. К счастью, такие пакеты для R есть. С одним из них — feasts — мы уже познакомились в гл. 4. Ниже будут рассмотрены возможности feasts по извлечению признаков из временных рядов на примере данных по стоимости 22 криптовалют (подразд. 1.5.1).

5.1 Функция features()

В пакете feasts извлечение признаков из временных рядов выполняется с помощью функции–менеджера features(), которая имеет следующие аргументы:

  • .tbl — таблица с данными (например, объект класса data.frame, tibble или tsibble);
  • .var — имя переменной в таблице .tbl, по значениям которой необходимо вычислить те или иные признаки;
  • features — список функций, которые непосредственно выполняют вычисления соответствующих признаков;
  • ... — дополнительные аргументы, которые необходимо подать на функции, перечисленные в списке features. Важно отметить, что такие аргументы будут переданы на ту или иную функцию, только если они входят в состав формальных аргументов этой функции, а не являются ее дополнительными аргументами (...). Например, в случае с базовой функцией var(), указание аргумента na.rm = TRUE сработает, поскольку это формальный аргумент var(). В то же время в случае с базовой функцией mean() это не сработает, поскольку na.rm является ее дополнительным аргументом. Чтобы убедиться в том, что необходимые аргументы будут поданы на нужную функцию, ее следует добавить в список features в виде анонимной функции, как показано в следующем примере:
## # A tibble: 22 x 2
##    coin              V1
##    <chr>          <dbl>
##  1 augur       23.2    
##  2 bitcoin   7492.     
##  3 cardano      0.136  
##  4 chainlink    0.938  
##  5 dash       223.     
##  6 decred      41.8    
##  7 dogecoin     0.00350
##  8 eos          6.08   
##  9 ethereum   340.     
## 10 iota         0.776  
## # ... with 12 more rows

Заметьте, что в последней команде нам не нужно было сначала сгруппировать данные по переменной coin — расчет средних значений для отдельных уровней этой переменной был выполнен автоматически. Такой результат стал возможным благодаря тому, что таблица dat_ts является объектом класса tsibble, в котором переменная coin служит “ключом”. Функции пакета feasts “знают” как работать с подобными объектами.

Другой момент, на который стоит обратить внимание: результатом выполнения последней команды стала таблица, в которой рассчитанная новая переменная имеет мало о чем говорящее название V1. Чтобы изменить такое поведение feasts, рекомендуется сначала сохранить определение анонимной функции в виде полноценной пользовательской функции. Эта функция должна возвращать вектор с одним или несколькими поименованными элементами — их имена в итоге станут именами соответствующих переменных в итоговой таблице. В приведенном ниже примере пользовательская функция my_func(x) возвращает вектор со значениями арифметического среднего и дисперсии x:

## # A tibble: 22 x 3
##    coin             avg     var
##    <chr>          <dbl>   <dbl>
##  1 augur       23.2     3.28e+2
##  2 bitcoin   7492.      6.72e+6
##  3 cardano      0.136   2.61e-2
##  4 chainlink    0.938   7.71e-1
##  5 dash       223.      4.66e+4
##  6 decred      41.8     7.46e+2
##  7 dogecoin     0.00350 3.46e-6
##  8 eos          6.08    1.23e+1
##  9 ethereum   340.      7.00e+4
## 10 iota         0.776   5.82e-1
## # ... with 12 more rows

5.2 Встроенные функции для расчета признаков

Помимо подаваемых на features() пользовательских функций можно также воспользоваться целым рядом готовых функций, входящих в состав пакета feasts. Например, для расчета коэффициента Xёрста и спектральной энтропии ряда служат функции coef_hurst() и feat_spectral():

## # A tibble: 22 x 3
##    coin      coef_hurst spectral_entropy
##    <chr>          <dbl>            <dbl>
##  1 augur           1.00            0.423
##  2 bitcoin         1.00            0.444
##  3 cardano         1.00            0.422
##  4 chainlink       1.00            0.437
##  5 dash            1.00            0.398
##  6 decred          1.00            0.422
##  7 dogecoin        1.00            0.535
##  8 eos             1.00            0.494
##  9 ethereum        1.00            0.407
## 10 iota            1.00            0.417
## # ... with 12 more rows

Некоторые встроенные в feasts функции возвращают сразу несколько признаков. Например, feat_stl() выполняет декомпозицию временного ряда на отдельные компоненты (гл. 4) и далее на их основе вычисляет различные величины, включая выраженность тренда (trend strength) и сезонной составляющей (seasonal strength), линейность (linearity) и кривизну (curvature) ряда и т.д. (Hyndman and Athanasopoulos 2019; Kang, Hyndman, and Smith-Miles 2017):

## Observations: 22
## Variables: 10
## $ coin                   <chr> "augur", "bitcoin", "car...
## $ trend_strength         <dbl> 0.9907166, 0.9908439, 0....
## $ seasonal_strength_week <dbl> 0.14638033, 0.21990784, ...
## $ seasonal_peak_week     <dbl> 6, 6, 6, 6, 6, 6, 6, 6, ...
## $ seasonal_trough_week   <dbl> 2, 2, 2, 2, 1, 4, 2, 2, ...
## $ spikiness              <dbl> 4.733049e-04, 6.274527e+...
## $ linearity              <dbl> -3.523179e+02, -4.067290...
## $ curvature              <dbl> 2.204012e+02, 5.028015e+...
## $ stl_e_acf1             <dbl> 0.40641299, 0.29884561, ...
## $ stl_e_acf10            <dbl> 0.4719425, 0.2286323, 0....

На момент написания этой книги пакет feasts позволял рассчитать 48 признаков, характеризующих различные свойства временных рядов. Для одновременного расчета всех этих признаков можно применить вспомогательную функцию feature_set() из пакета fabletools (гл. 4) следующим образом:

## # A tibble: 22 x 49
##    coin  trend_strength seasonal_streng~ seasonal_peak_w~ seasonal_trough~
##    <chr>          <dbl>            <dbl>            <dbl>            <dbl>
##  1 augur          0.991            0.146                6                2
##  2 bitc~          0.991            0.220                6                2
##  3 card~          0.990            0.249                6                2
##  4 chai~          0.996            0.226                6                2
##  5 dash           0.996            0.312                6                1
##  6 decr~          0.993            0.232                6                4
##  7 doge~          0.983            0.303                6                2
##  8 eos            0.988            0.274                6                2
##  9 ethe~          0.995            0.159                6                4
## 10 iota           0.995            0.228                6                2
## # ... with 12 more rows, and 44 more variables: spikiness <dbl>,
## #   linearity <dbl>, curvature <dbl>, stl_e_acf1 <dbl>, stl_e_acf10 <dbl>,
## #   acf1 <dbl>, acf10 <dbl>, diff1_acf1 <dbl>, diff1_acf10 <dbl>,
## #   diff2_acf1 <dbl>, diff2_acf10 <dbl>, season_acf1 <dbl>, pacf5 <dbl>,
## #   diff1_pacf5 <dbl>, diff2_pacf5 <dbl>, season_pacf <dbl>,
## #   zero_run_mean <dbl>, nonzero_squared_cv <dbl>, zero_start_prop <dbl>,
## #   zero_end_prop <dbl>, lambda_guerrero <dbl>, kpss_stat <dbl>,
## #   kpss_pvalue <dbl>, pp_stat <dbl>, pp_pvalue <dbl>, ndiffs <int>,
## #   nsdiffs <int>, bp_stat <dbl>, bp_pvalue <dbl>, lb_stat <dbl>,
## #   lb_pvalue <dbl>, var_tiled_var <dbl>, var_tiled_mean <dbl>,
## #   shift_level_max <dbl>, shift_level_index <dbl>, shift_var_max <dbl>,
## #   shift_var_index <dbl>, shift_kl_max <dbl>, shift_kl_index <dbl>,
## #   spectral_entropy <dbl>, n_crossing_points <int>, n_flat_spots <int>,
## #   coef_hurst <dbl>, stat_arch_lm <dbl>

Функция feature_set() имеет два аргумента: pkgs — вектор с названиями пакетов, функции из которых вычисляют те или иные признаки, и tags — вектор с “метками”, обозначающими группы тематически сходных признаков. В приведенной выше команде мы запросили вычисление всех признаков, реализованных в пакете feasts (feature_set(pkgs = "feasts")). Однако часто более удобным и гибким подходом для формирования списка признаков будет использование аргумента tags. Например, команда feature_set(tags = c("stl", "spectral")) приведет к вычислению всех признаков, возвращаемых функциями feat_stl() и feat_spectral() (см. выше). Список меток всех признаков, реализованных в пакете feasts, можно просмотреть с помощью команды ?features_by_tag. Этот список и краткие пояснения к нему приведены ниже (названия меток выделены жирным шрифтом; после названия каждой метки идут краткое пояснение и список функций, непосредственно выполняющих соответствующие вычисления):

acf

Набор признаков, рассчитываемых на основе коэффициентов автокорреляции.

  • feat_acf()

autocorrelation

Набор признаков, рассчитываемых на основе коэффициентов автокорреляции и частных коэффициентов автокорреляции.

  • feat_acf()
  • feat_pacf()

boxcox

Оптимальное значение параметра \(\lambda\) для преобразования Бокса–Кокса.

  • guerrero()

coefficients

Коэффициент Хёрста.

  • coef_hurst()

count

Количество раз, когда временной ряд пересекает свою собственную медиану, и максимальная длина временного отрезка, в пределах которого наблюдения имеют одинаковые значения:

  • n_crossing_points()
  • n_flat_spots()

decomposition

Признаки, рассчитываемые на основе компонент временного ряда.

  • feat_stl()

intermittent

Признаки, отражающие наличие и структуру временных отрезков, в пределах которых все значения ряда равны нулю.

  • feat_intermittent()

lumpiness

Дисперсия дисперсий, рассчитанных по наблюдениям из непересекающихся временных отрезков (окон).

  • var_tiled_var()

optimisation

То же, что и метка boxcox выше, т.е. оптимальное значение параметра \(\lambda\) для преобразования Бокса–Кокса.

  • guerrero()

pacf

Набор признаков, рассчитываемых на основе частных коэффициентов автокорреляции.

  • feat_pacf()

portmanteau

Статистики, рассчитываемые в результате применения тестов Льюнг–Бокса и Бокса–Пирса на наличие автокорреляции в данных.

  • box_pierce()
  • ljung_box()

rle

Максимальная длина временного отрезка, в пределах которого значения ряда принадлежат к одному из децилей.

  • n_flat_spots()

roll

Признаки, рассчитываемые по данным из пересекающихся временных отрезков (окон), в частности максимальный сдвиг среднего уровня, дисперсии и расстояния Кульбака–Лейблера в следующих друг за другом отрезках.

  • shift_level_max()
  • shift_var_max()
  • shift_kl_max()

seasonal

Признаки, рассчитываемые на основе компонент временного ряда, а также минимальное число дифференцирований ряда, необходимое для достижения его стационарности.

  • feat_stl()
  • unitroot_nsdiffs()

slide

То же, что и метка roll (см. выше).

spectral

Спектральная энтропия ряда.

  • feat_spectral()

stability

Максимальный сдвиг среднего уровня, рассчитанного по данным из двух пересекающихся временных отрезков (окон).

  • var_tiled_mean()

stl

Признаки, рассчитываемые на основе компонент временного ряда.

  • feat_stl()

test

Статистики, рассчитываемые в ходе различных тестов (на наличие автокорреляции, единичного корня, авторегрессионной условной гетероскедастичности и др.).

  • unitroot_kpss()
  • unitroot_pp()
  • unitroot_ndiffs()
  • unitroot_nsdiffs()
  • box_pierce()
  • ljung_box()
  • stat_arch_lm()

tile

Признаки, рассчитываемые по данным из непересекающихся временных отрезков (окон), в частности дисперсия дисперсий и дисперсия средних значений.

  • var_tile_mean()
  • var_tile_var()

trend

То же, что и метка stl.

unitroot

Статистики, рассчитываемые в ходе тестов на наличие в данных единичного корня, а также минимальное число дифференцирований ряда, необходимое для достижения его стационарности.

  • unitroot_kpss()
  • unitroot_pp()
  • unitroot_ndiffs()
  • unitroot_nsdiffs()

Пользовательские функции тоже можно сделать “видимыми” для feature_set(). Для этого их необходимо зарегистрировать с помощью вспомогательной функции register_feature():

## Observations: 22
## Variables: 3
## $ coin <chr> "augur", "bitcoin", "cardano", "chainlink"...
## $ avg  <dbl> 2.315007e+01, 7.491721e+03, 1.359970e-01, ...
## $ var  <dbl> 3.283892e+02, 6.722352e+06, 2.614519e-02, ...

5.3 Примеры использования извлеченных признаков

Описанные в предыдущем разделе признаки позволяют проанализировать и понять свойства сразу нескольких временных рядов. Представим, например, что перед нами стоит задача выявить временные ряды с наименьшей и наибольшей выраженностью тренда. Это можно было бы сделать следующим образом (рис. 5.1):

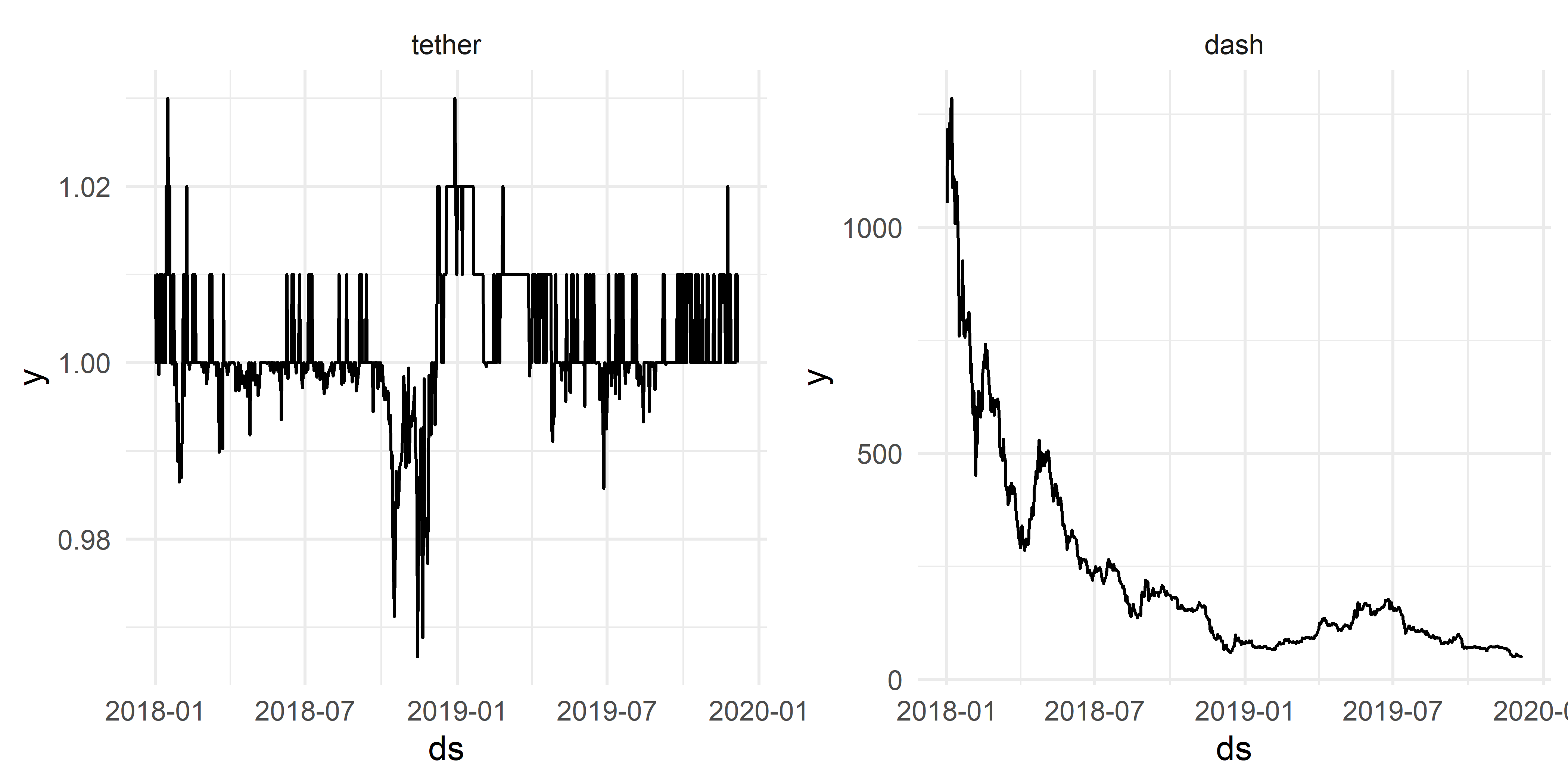
Временные ряды из набора данных cryptos с минимальной (слева) и максимальной (справа) выраженностью тренда

РИСУНОК 5.1: Временные ряды из набора данных cryptos с минимальной (слева) и максимальной (справа) выраженностью тренда

Другой вопрос, на который было бы интересно ответить: какие ряды необычны по сочетанию нескольких признаков одновременно? Посмотрим, например, как выглядит распределение анализируемых рядов по выраженности тренда и недельной сезонности (рис. 5.2):

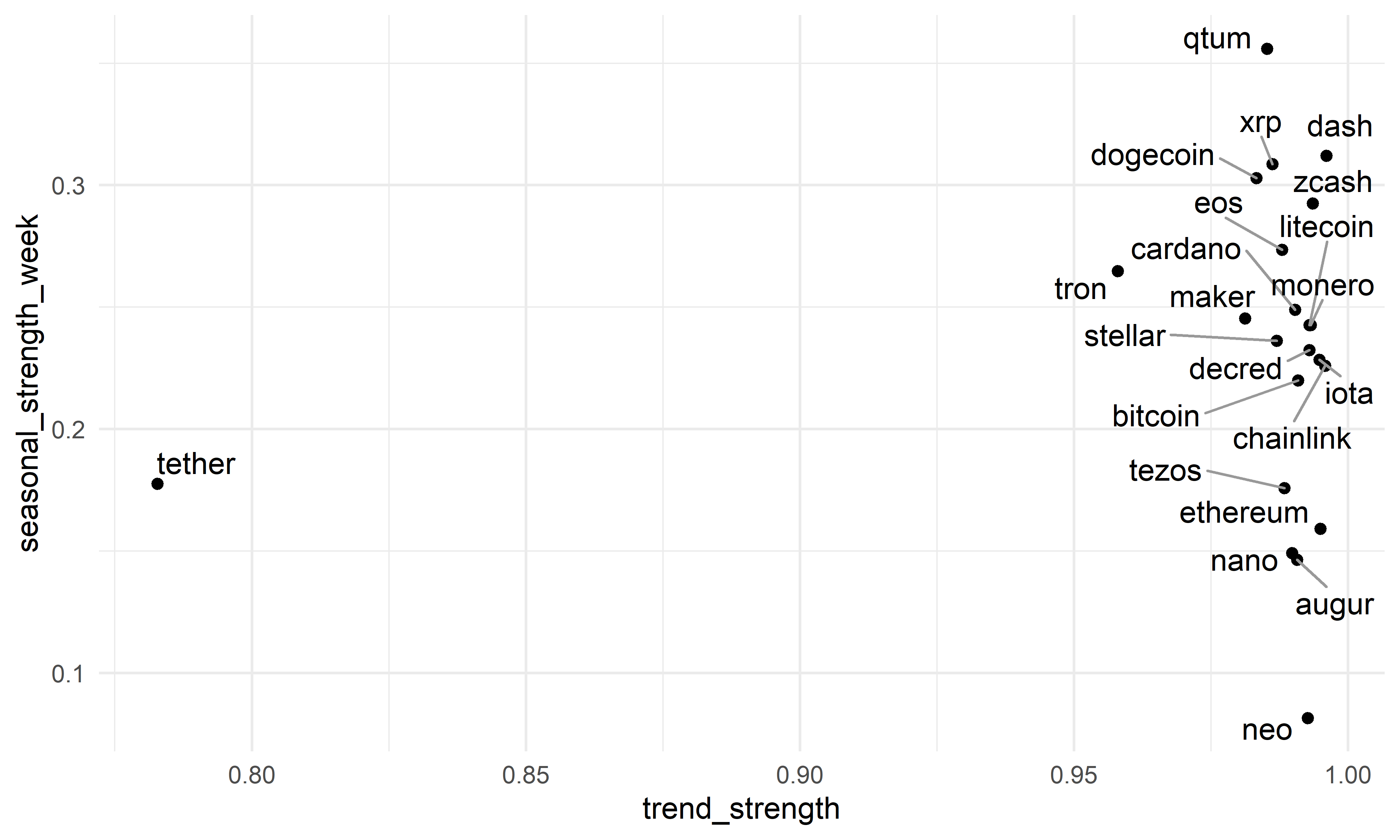
Распределение временных рядов из набора данных cryptos в соответствии с выраженностью тренда и недельной сезонности

РИСУНОК 5.2: Распределение временных рядов из набора данных cryptos в соответствии с выраженностью тренда и недельной сезонности

На рис. 5.2 четко выделяется временной ряд tether, для которого характерны низкие значения обоих показателей. Мы уже видели, как выглядит этот временной ряд (см. рис. 5.1 слева). Изобразим теперь и данные по криптовалюте qtum, которая характеризуется необычно высокой выраженностью как тренда, так и недельной сезонности (рис. 5.3):

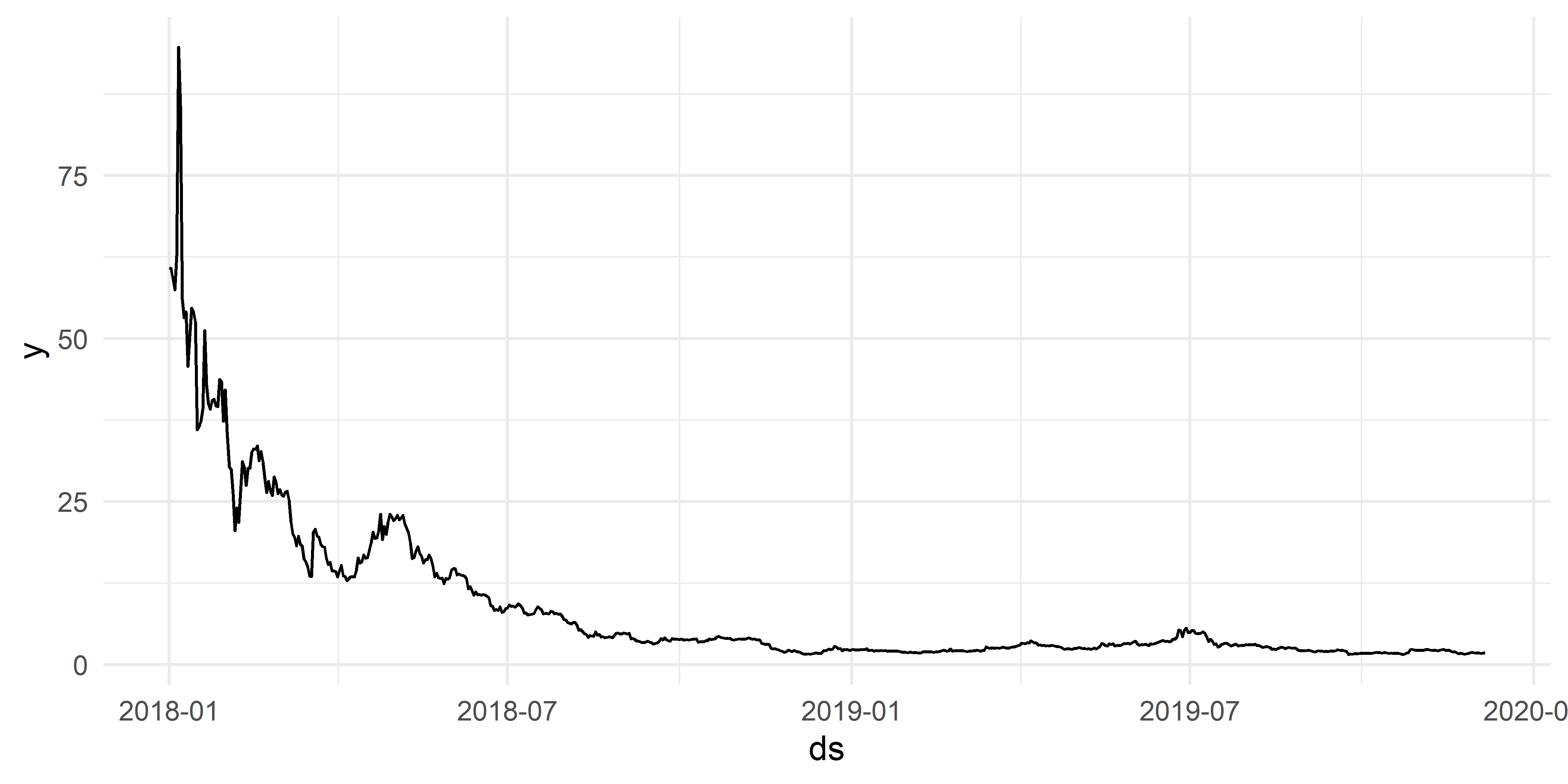
Динамика стоимости криптовалюты qtum

РИСУНОК 5.3: Динамика стоимости криптовалюты qtum

Мы можем пойти еще дальше и проанализировать данные из таблицы cryptos с помощью метода главных компонент (PCA) одновременно по всем признакам с ненулевой дисперсией (обратите внимание на логарифмирование исходных значений y, выполненное для снижения дисперсии в отдельных рядах и различий между рядами):

Согласно полученному результату (не приведен для экономии места), первые две главные компоненты объясняют примерно 56% всей дисперсии в данных. Изобразим все временные ряды в системе координат, образованной этими двумя главными компонентами (рис. 5.4):

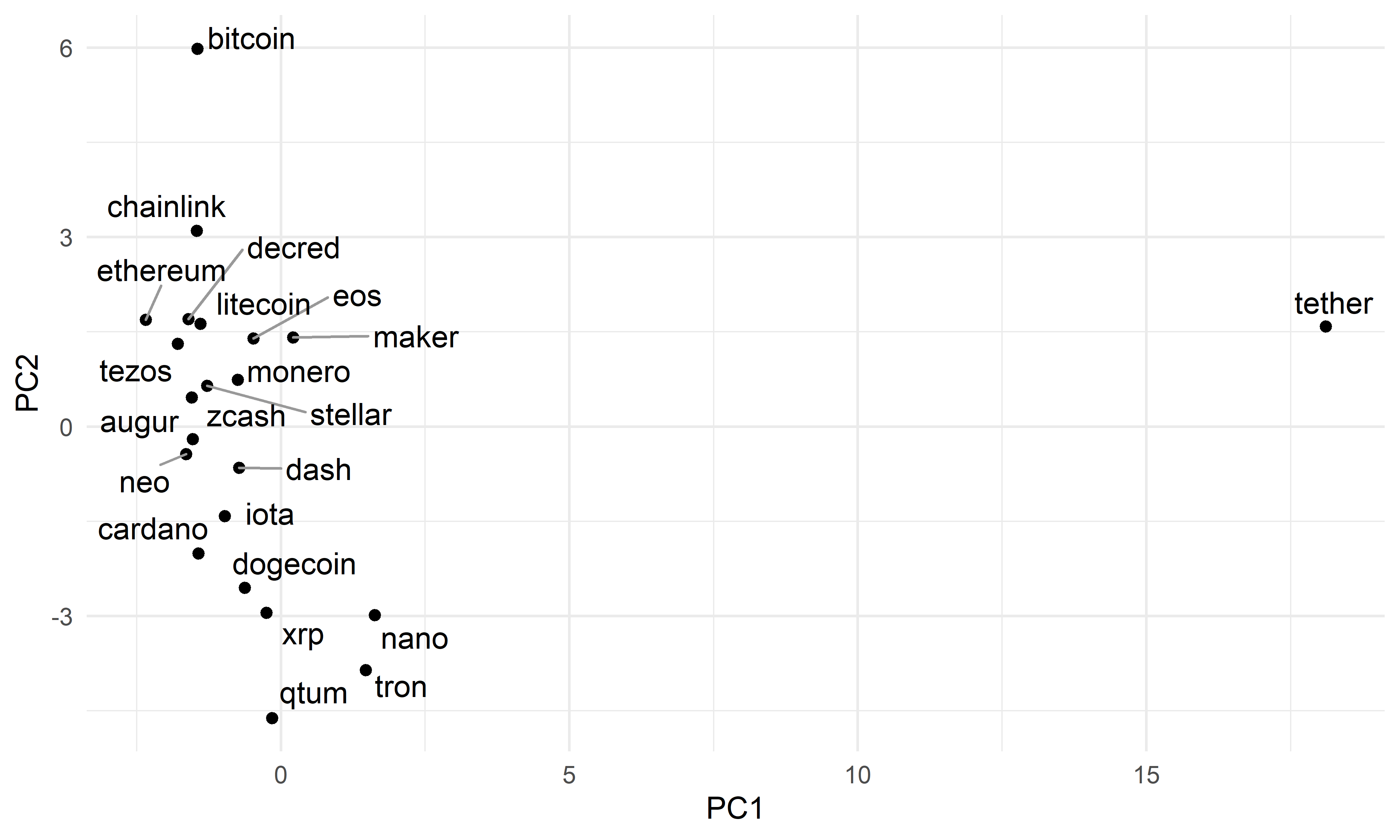
Распределение временных рядов из таблицы cryptos в соответствии со значениями первых двух главных компонент

РИСУНОК 5.4: Распределение временных рядов из таблицы cryptos в соответствии со значениями первых двух главных компонент

PCA–анализ по совокупности нескольких десятков признаков еще раз подтвердил аномальность временного ряда tether, а также подчеркнул необычность ряда bitcoin. Следует отметить, что этот анализ был выполнен в демонстрационных целях: аномальность tether легко заметить и без применения PCA — достаточно изобразить все имеющиеся временные ряды на одном графике (см. рис. 1.2, где этот ряд выглядит практически как горизонтальная линия). Тем не менее, во многих реальных ситуациях приходится иметь дело с сотнями и даже тысячами временных рядов, простое визуальное исследование которых невозможно. Описанный выше подход в сочетании с определенным методом обнаружения аномалий помог бы выявить необычные временные ряды в автоматическом режиме.