2.4 Проецирование многомерных данных на плоскости
Многомерный анализ (Кендалл, Стьюарт, 1976) представляет собой часть статистики, которая выполняет обработку и интерпретацию результатов, полученных на основе наблюдений одновременно нескольких взаимосвязанных случайных переменных, каждая из которых представляется одинаково важной, по крайней мере, первоначально. В случае, если данные измерены в метрических шкалах и предполагаются линейные отношения между переменными, то в анализе применяются многомерные статистические методы, основанные на операциях матричной алгебры.
Во многих задачах обработки многомерных наблюдений исследователя интересует, в первую очередь, возможность снижения размерности, т.е. способ выделения небольшого набора исходных признаков или их линейных комбинаций, которые в наибольшей степени объясняют изменчивость наблюдаемых объектов. Это обусловлено следующими тремя причинами: а) возможностью наглядного представления (визуализация и ординация); б) стремлению к лаконизму исследуемых моделей и в) необходимостью сжатия объемов информации (Айвазян и др., 1989).
Принцип ординации наблюдений (нем. Ordnung) заключается в использовании различных методов оптимального целенаправленного проецирования (projecting pursuit) облака точек из многомерного пространства в пространство малой размерности (с 2 или 3 осями координат). Для этого используются различные методы или их модификации, но в целом сущность ординации заключается в представлении исходной матрицы данных \(\mathbf Y\) в виде совокупности \(p\) латентных переменных \(\mathbf F\): \[Y_1, Y_2, \dots, Y_m \Rightarrow F_1, F_2, \dots, F_p,\] которые и являются осями ординационной диаграммы (двумерной при \(р = 2\) или трехмерной в случае с тремя такими латентными переменными). Выбор осей ординации осуществляется с использованием принципа оптимальности: стремления достичь минимума потерь содержательной информации, имеющейся в исходных данных.
Как правило, первая ось \(F_1\) проводится через центр сгущения значений \(y_{ij}\) и совпадает с направлением наибольшей по длине оси эллипсоида рассеяния. Вторая ось \(F_2\), также проходит через центр распределения, но проводится перпендикулярно к первой и совпадает по направлению со второй из главных полуосей эллипсоида рассеяния. Эта операция обеспечивает формирование “картинки” данных с минимально возможными искажениями, а новые обобщающие переменные \(F_1\) и \(F_2\) становятся ортогональными (т.е. взаимно некоррелированными, независимыми).
Большинство методов снижения размерности основано на анализе собственных значений и собственных векторов, который является важнейшим разделом линейной (матричной) алгебры. В кратком изложении суть преобразований \(\mathbf Y \Rightarrow \mathbf F\) заключается в следующем:
- Нахождение собственных значений и собственных векторов осуществляется в ходе математической операции линейного преобразования квадратной симметричной матрицы C размерностью \(m\). Это может быть любая матрица дистанций, но чаще всего используется дисперсионно-ковариационная матрица \(\mathbf C = \mathbf Y' \mathbf Y /(n - 1)\) стандартизованных исходных данных.
- Coбственными значениями квадратной матрицы \(\mathbf C\) называются такие значения \(\lambda_k\), при которых система \(m\) уравнений вида \((\mathbf{C} - \lambda_k \mathbf{I})\mathbf{u}_k = \mathbf{0}\) имеет нетривиальное решение. Здесь \(\mathbf{u}_k\) - собственные векторы матрицы \(\mathbf{C}\), соответствующие \(\lambda_k\), \(k = 1, 2, \dots, m\), \(\mathbf{I}\) - единичная матрица.
- Матрица из \(k\) собственных векторов \(\mathbf{U}_k\) представляет собой веса для пересчета из исходного в редуцированное информационное пространство, т.е. матрицы переменных \(\mathbf Y\) и \(\mathbf F\) связаны соотношением \(\mathbf{F}_{n \times k} = \mathbf{Y}_{n \times m} \mathbf{U}_{m \times k}\).
- Каждое собственное значение \(\lambda_k\) соответствует величине дисперсии, объясняемой на \(k\)-м уровне, т.е. сумма всех собственных значений будет равняться сумме дисперсий всех исходных переменных.
- Ряд собственных значений обычно ранжируется от самого большого до минимального: первое собственное значение \(\lambda_1\), объясняющее наибольшую долю вариации данных, часто называют “доминирующим” или “ведущим”. Значения \(\lambda_1\) и \(\lambda_2\) определяют меру значимости осей \(F_1\) и \(F_2\) ординационной диаграммы, т.е. концентрацию исходных точек вдоль каждой оси и, в итоге, ее выраженность.
- Собственные значения \(\lambda_k\) находят в ходе итерационной процедуры, и точность их вычисления зависит от степени обусловленности исходной матрицы \(\mathbf C\).
Классическим методом снижения размерности данных является анализ главных компонент (PCA, Principal Components Analysis), который широко используется в различных областях науки и техники и детально описан в многочисленных руководствах (ter Braak, 1983; Айвазян и др., 1989; Джонгман и др., 1999; Legendre, Legendre, 2012).
Снижение размерности исходного пространства методом PCA можно представить как последовательный, итеративный процесс, который можно оборвать на любом шаге \(u\). Вследствие ортогональности системы координат главных компонент (т.е. фактически, их взаимной независимости) нет необходимости перестраивать матрицы счетов (scores) \(\mathbf F\) и нагрузок (loadings) \(\mathbf U\) при изменении числа компонент: последующие столбцы или строки просто прибавляются или отбрасываются.
Используем в качестве примера идентификацию типа оконных стекол (Glass Identification) по выборке, представленный в коллекции баз данных UCI Machine Learning Repository. Существует два основных способа производства листового стекла: горизонтальный на расплаве олова (флэш-стекло) и по принципу вертикального вытягивания. Термически полированное флэш-стекло отличается идеально глянцевой поверхностью, высокой светопропускающей способностью и великолепными оптическими свойствами, исключающими искажение изображения.
В ходе криминалистической экспертизы мельчайших осколков стекла можно определить их оптическую рефракцию (RI) и сделать химический анализ содержания окислов основных элементов. Ставится вопрос, можно ли по этим данным выполнить прогноз типа производства стекла Сlass. Исходные данные представлены в файле Glass.txt3 и можно предварительно рассмотреть описательные статистики отдельных переменных:
DGlass <- read.table(file = "data/Glass.txt", sep = ",",
header = TRUE, row.names = 1)print(t(apply(DGlass[, -10], 2, function(x) {
c(Минимум = min(x), Максимум = max(x),
Среднее = mean(x), Отклонение = sd(x),
Корреляция = cor(x, DGlass$Class)) # признаков с Class
})), 3)## Минимум Максимум Среднее Отклонение Корреляция
## RI 1.51 1.53 1.5186 0.00305 -0.0601
## Na 10.73 14.86 13.2017 0.58830 0.0186
## Mg 0.00 4.49 3.2949 0.88778 -0.1462
## Al 0.29 2.12 1.2817 0.32374 0.1998
## Si 69.81 74.45 72.5869 0.64117 -0.0785
## K 0.00 1.10 0.4775 0.21873 0.0386
## Ca 7.08 16.19 8.9247 1.37263 0.0446
## Ba 0.00 3.15 0.0298 0.25353 0.0312
## Fe 0.00 0.37 0.0676 0.09951 0.0532В среде R расчет главных компонент может быть осуществлен с использованием функций princomp() или prcomp(), но мы будем ориентироваться на многообразие возможностей пакета vegan() и его функцию rda(). Протокол анализа ограничим четырьмя главными компонентами, объясняющими 98% общей вариации данных:
library(vegan)
Y <- as.data.frame(DGlass[, 1:9])
mod.pca <- vegan::rda(Y ~ 1)
head(summary(mod.pca))##
## Call:
## rda(formula = Y ~ 1)
##
## Partitioning of variance:
## Inertia Proportion
## Total 3.656 1
## Unconstrained 3.656 1
##
## Eigenvalues, and their contribution to the variance
##
## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6
## Eigenvalue 2.6056 0.5828 0.21129 0.18895 0.04308 0.01403
## Proportion Explained 0.7126 0.1594 0.05779 0.05168 0.01178 0.00384
## Cumulative Proportion 0.7126 0.8720 0.92984 0.98152 0.99330 0.99714
## PC7 PC8 PC9
## Eigenvalue 0.008907 0.001562 6.952e-07
## Proportion Explained 0.002440 0.000430 0.000e+00
## Cumulative Proportion 0.999570 1.000000 1.000e+00
##
## Scaling 2 for species and site scores
## * Species are scaled proportional to eigenvalues
## * Sites are unscaled: weighted dispersion equal on all dimensions
## * General scaling constant of scores: 4.93332
##
##
## Species scores
##
## PC1 PC2 PC3 PC4 PC5 PC6
## RI -0.006663 0.003040 -0.001587 -0.0007297 0.0005398 9.075e-05
## Na 0.461583 1.180084 0.833131 0.0499341 0.0109644 2.782e-03
## Mg 2.037591 0.659746 -0.616211 -0.5223737 -0.0598691 4.080e-02
## Al 0.240546 -0.337483 -0.107770 0.6588300 -0.2282742 1.616e-01
## Si 0.691702 -1.339222 0.458279 -0.4986449 0.0521649 4.062e-02
## K 0.265988 -0.302647 -0.111021 0.2512089 -0.1346813 -2.370e-01
## Ca -3.512043 0.228783 -0.158561 -0.3491594 -0.0734353 2.515e-02
## Ba -0.190199 -0.009844 -0.267021 0.3372595 0.4523324 1.708e-02
## Fe -0.039086 -0.017137 -0.046526 0.0299297 0.0074709 -8.279e-02
##
##
## Site scores (weighted sums of species scores)
##
## PC1 PC2 PC3 PC4 PC5 PC6
## 1 0.1468 0.65354 -0.45248 -0.29870 -0.042920 0.93669
## 2 0.2831 0.14066 0.44579 0.17972 0.156651 0.10489
## 3 0.2893 -0.07868 0.33811 0.17331 0.112400 0.71176
## 4 0.1923 0.01262 -0.08129 0.03596 0.003594 -0.17275
## 5 0.2337 -0.14621 0.16040 -0.10747 0.193631 -0.07327
## 6 0.2215 -0.29717 -0.20023 0.14445 -0.180684 0.05884
## ....Рассмотрим, какую конфигурацию имеет распределение наблюдений в пространстве первых двух главных компонент PC1 и PC2. Наибольший интерес для нас представляет взаимное расположение сгущений точек, принадлежащих стеклам двух типов: Class = {1, 3} - оконное и автомобильное флэш-стекло, и Class = 2 - тянутое стекло. Выполним построение ординационной диаграммы с использованием пакета ggplot2 (рис. 2.11):
FAC <- as.factor(ifelse(DGlass$Class == 2, 2, 1))
pca.scores <- as.data.frame(summary(mod.pca)$sites[, 1:2])
pca.scores <- cbind(pca.scores, FAC)
# Составляем таблицу для "каркаса" точек на графике:
l <- lapply(unique(pca.scores$FAC), function(c)
{ f <- subset(pca.scores, FAC == c); f[chull(f), ]})
hull <- do.call(rbind, l)
# Включаем в названия осей доли объясненной дисперсии:
axX <- paste("PC1 (", as.integer(100*mod.pca$CA$eig[1]/sum(mod.pca$CA$eig)), "%)")
axY <- paste("PC2 (", as.integer(100*mod.pca$CA$eig[2]/sum(mod.pca$CA$eig)), "%)")
# Выводим ординационную диаграмму:
ggplot() +
geom_polygon(data = hull,
aes(x = PC1, y = PC2, fill = FAC), alpha = 0.4, linetype = 0) +
geom_point(data = pca.scores,
aes(x = PC1, y = PC2, shape = FAC, colour = FAC), size = 3) +
scale_colour_manual(values = c('purple', 'blue')) +
xlab(axX) + ylab(axY) + coord_equal() + theme_bw()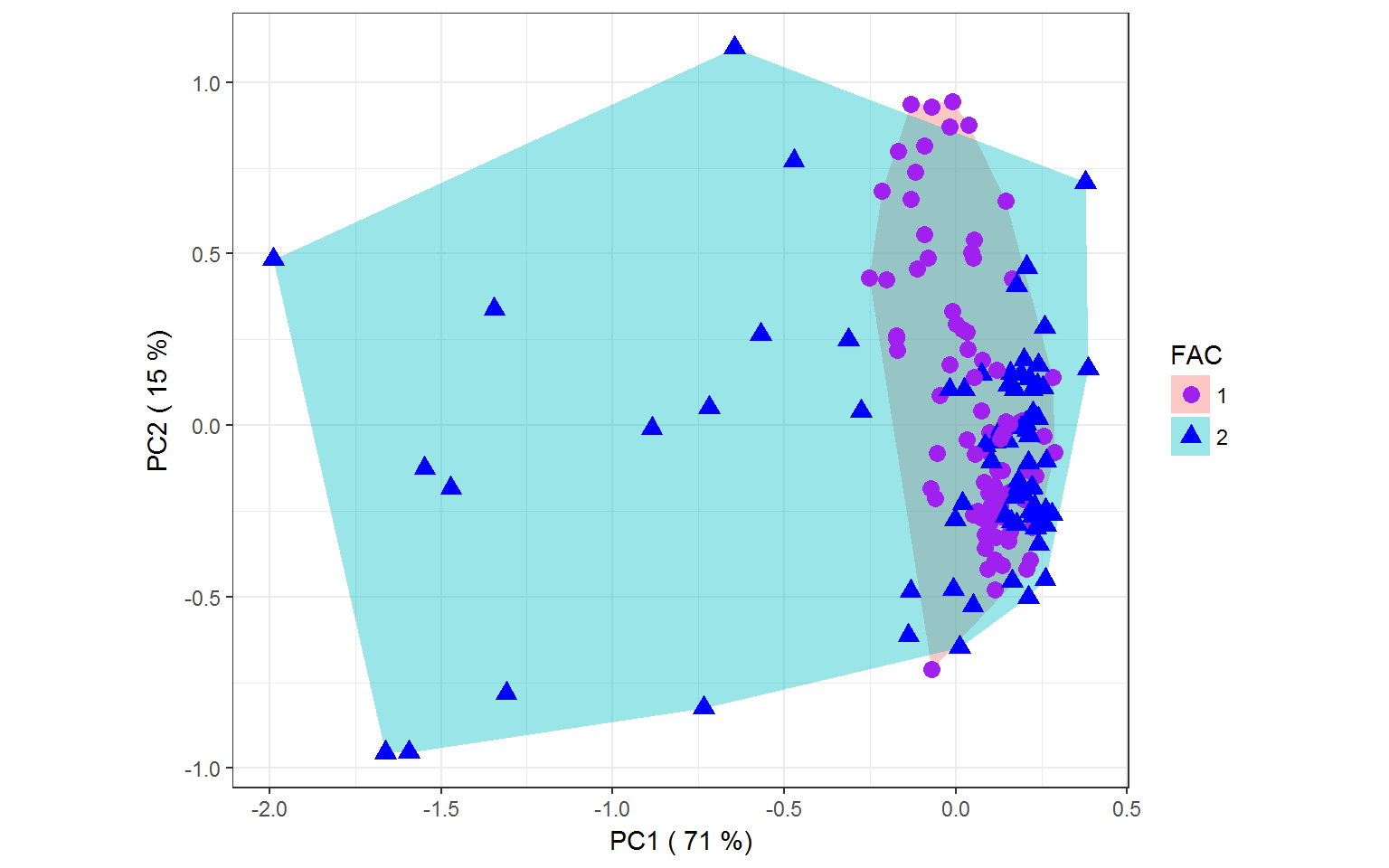
Рисунок 2.10: Ординационная диаграмма, построенная методом PCA
Заметим, что для выделения наблюдений каждого класса на диаграммах обычно применяются четыре вспомогательных графических объекта: а) “каркас” (hull) или контур, проводимый через крайние точки, как мы это выполнили на рис. 2.10; б) эллипс, ограничивающий, например, 95% наблюдений; в) точка центроида или “центра тяжести” облака точек; г) “паук” (spider), т.е. набор линий, соединяющих каждую точку с центроидом своего класса.
По существу расчетов можно отметить следующее:
- первая главная компонента объясняет 71% совокупной дисперсии в данных, а \(F_1\) и \(F_2\) совместно - 87%, что является вполне обнадеживающим результатом;
- ось
РС1в значительной мере определяется содержанием магния и кальция, а осьРС2- концентрациями натрия и кремния; - диаграмма на рис. 2.10 показывает, что химический состав флэш-стекла в целом не отличается от тянутого, но для него не характерно повышенное содержание кальция (точки левее
РС1 = -0.5).
Итак, ординация показала, что облака точек обоих классов являются плохо разделяемыми. Обратим внимание, что в расчетах не использовался такой ключевой показатель, как тип производства стекла, известный нам по примерам обучающей выборки.
Этот файл можно найти в репозитории с приложениями к книге.↩