ГЛАВА 5 Бинарные матрицы и ассоциативные правила
5.1 Классификация в бинарных пространствах с использованием классических моделей
Большое количество задач связано с нахождением закономерностей в пространствах бинарных переменных: расшифровка геномного кода, анализ пиков на спектрофотометрах, обработка социологических анкет с ответами “Да/Нет” и т.д. Методы анализа таких выборок рассмотрим на не слишком серьезном примере, фигурирующем в книге Дюка и Самойленко (2001).
Предположим, что некая избирательная комиссия озаботилась выделением характерных черт групп электората, голосующих за различные общественные платформы. На представленном рис. 5.1 схематично изображены лица людей, относящихся к двум классам (для определенности пусть это будут “Патриоты” и “Демократы”). Ставится задача найти комбинации признаков, характеризующие это разделение.
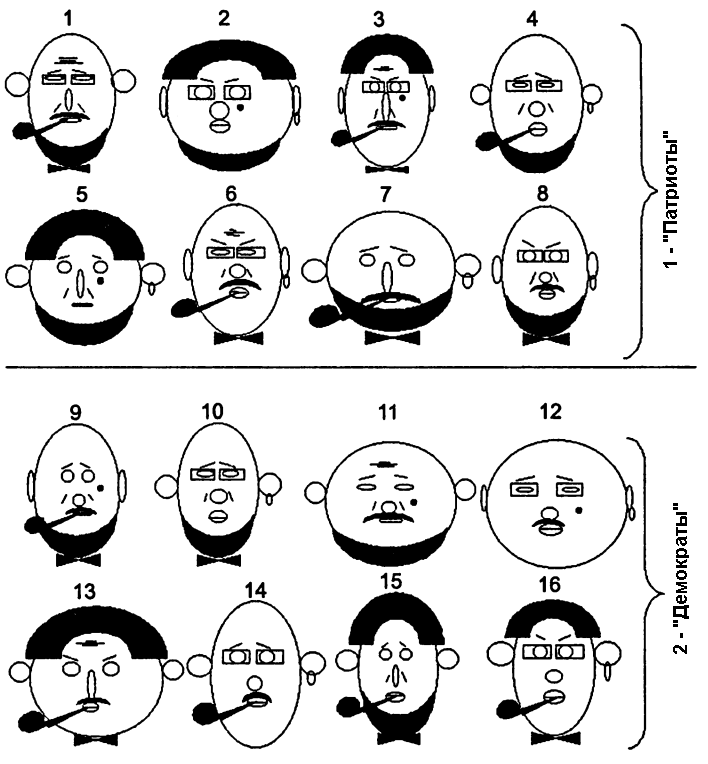
Рисунок 5.1: Изображения лиц людей, относящихся к двум различным классам (Дюк, Самойленко, 2001)
Скорее всего, визуальный анализ, проведенный читателем, с большими трудностями позволит определить, чем лица разных классов отличаются друг от друга и что объединяет лица одного класса. Даже такую, на первый взгляд простую, задачу обнаружения скрытых закономерностей лучше поручить компьютерным методам анализа данных.
Прежде всего, выделим признаки, характеризующие изображенные лица. Это следующие характеристики:
\(x_1\) (голова) – круглая (1) или овальная (0);
\(x_2\) (уши) – оттопыренные (1) или прижатые (0);
\(x_3\) (нос) – круглый (1) или длинный (0);
\(x_4\) (глаза) – круглые (1) или узкие (0);
\(x_5\) (лоб) – с морщинами (1) или без морщин (0);
\(x_6\) (носогубная складка) – есть (1) или нет (0);
\(x_7\) (губы) – толстые (1) или тонкие (0);
\(x_8\) (волосы) – есть (1) или нет (0);
\(x_9\) (усы) – есть (1) или нет (0);
\(x_{10}\) (борода) – есть (1) или нет (0);
\(x_{11}\) (очки) – есть (1) или нет (0);
\(x_{12}\) (родинка на щеке) – есть (1) или нет (0);
\(x_{13}\) (бабочка) – есть (1) или нет (0);
\(x_{14}\) (брови) – подняты кверху (1) или опущены книзу (0);
\(x_{15}\) (серьга) – есть (1) или нет (0);
\(x_{16}\) (курительная трубка) – есть (1) или нет (0).
Загрузим исходную матрицу данных, соответствующую изображенным лицам, cтроки которой соответствуют объектам (\(n\) = 16), а столбцы - выделенным бинарным признакам (\(m\) = 16). Объекты с номерами 1-8 относятся к классу 1, а с номерами 9-16 - к классу 2.
DFace <- read.delim(file = "data/Faces.txt", header = TRUE, row.names = 1)
head(DFace, 8)## x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 Class
## 1 0 1 0 0 1 1 0 0 1 1 1 0 1 1 0 1 1
## 2 1 0 1 1 0 0 1 1 0 1 1 1 0 0 1 0 1
## 3 0 0 0 1 1 1 0 1 1 0 1 1 1 0 0 1 1
## 4 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 1 1
## 5 1 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 1
## 6 0 0 1 0 1 1 1 0 1 0 1 0 1 0 1 1 1
## 7 1 1 0 1 0 0 0 0 1 1 0 0 1 1 1 1 1
## 8 0 0 1 1 0 1 1 0 1 1 1 0 1 0 1 0 1Попытаемся решить поставленную задачу с помощью классических статистических методов. Множественная логистическая регрессия - один из распространенных подходов к моделированию значений отклика, заданного альтернативной шкалой 0/1 (Мастицкий, Шитиков, 2015).
Если \(\boldsymbol{x}\) - вектор значений \(m\) независимых переменных, то вероятность \(P\) того, что отклик y примет значение 1, может быть описана моделью
\[P(y = 1|\boldsymbol{x}) \equiv p(\boldsymbol{x}) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_m x_m,\]
которая после оценки коэффициентов регрессии \(\beta_i\) будет возвращать искомую вероятность на интервале [0, 1]. Для того, чтобы обеспечить линейность функции относительно предикторов \(x_i\) и робастность процедуры подбора коэффициентов, модель переписывают как функцию логита:
\[g(y) = \log \left( \frac{p(\boldsymbol{x})}{1 - p(\boldsymbol{x})} \right) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_m x_m.\]
Неизвестные параметры модели \(\beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_m x_m\) обычно находят с использованием функции максимального правдоподобия, а предсказанный результат \(g(y)\) трансформируют обратно в вероятности \(p(\boldsymbol{x})\) в диапазоне между 0 и 1.
Построенной модели регрессии при использовании представленных данных и полного комплекта переменных \(m\) = 16 соответствует значение критерия Акаике AIC = 28. Компактную модель логита, состоящую только из 7 переменных, можно получить в ходе селекции набора информативных переменных на основе стандартной пошаговой процедуры step():
logit <- glm((Class - 1) ~ ., data = DFace, family = binomial)
logit.step <- step(logit, trace = 0)
summary(logit.step)##
## Call:
## glm(formula = (Class - 1) ~ x2 + x3 + x4 + x5 + x7 + x13 + x14,
## family = binomial, data = DFace)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -5.479e-06 -4.277e-06 0.000e+00 3.274e-06 6.239e-06
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -329.06 763966.35 0 1
## x2 50.59 190798.82 0 1
## x3 101.32 274757.62 0 1
## x4 102.33 279732.64 0 1
## x5 101.83 278492.43 0 1
## x7 50.59 190798.82 0 1
## x13 49.90 202466.80 0 1
## x14 101.32 274757.62 0 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2.2181e+01 on 15 degrees of freedom
## Residual deviance: 2.2719e-10 on 8 degrees of freedom
## AIC: 16
##
## Number of Fisher Scoring iterations: 25Значение информационного критерия значительно снизилось, остаточный девианс практически равен 0, но при этом все оцененные коэффициенты оказались статистически незначимыми. Вероятно, параметрический алгоритм оценки значимости коэффициентов не вполне работоспособен при небольшом числе измерений и/или особой конфигурации данных. Однако насколько эффективен построенный классификатор при предсказании? Рассчитаем число выполненных ошибок и таблицу неточностей:
mp <- predict(logit.step, type = "response")
pred = ifelse(mp > 0.5, 2, 1)
CTab <- table(Факт = DFace$Class, Прогноз = pred)
Acc = mean(pred == DFace$Class)
paste("Точность=", round(100*Acc, 2), "%", sep = "") ## [1] "Точность=100%"barplot(mp - 0.5, col = "steelblue", xlab = "Члены выборки",
ylab = "Вероятности P - 0.5")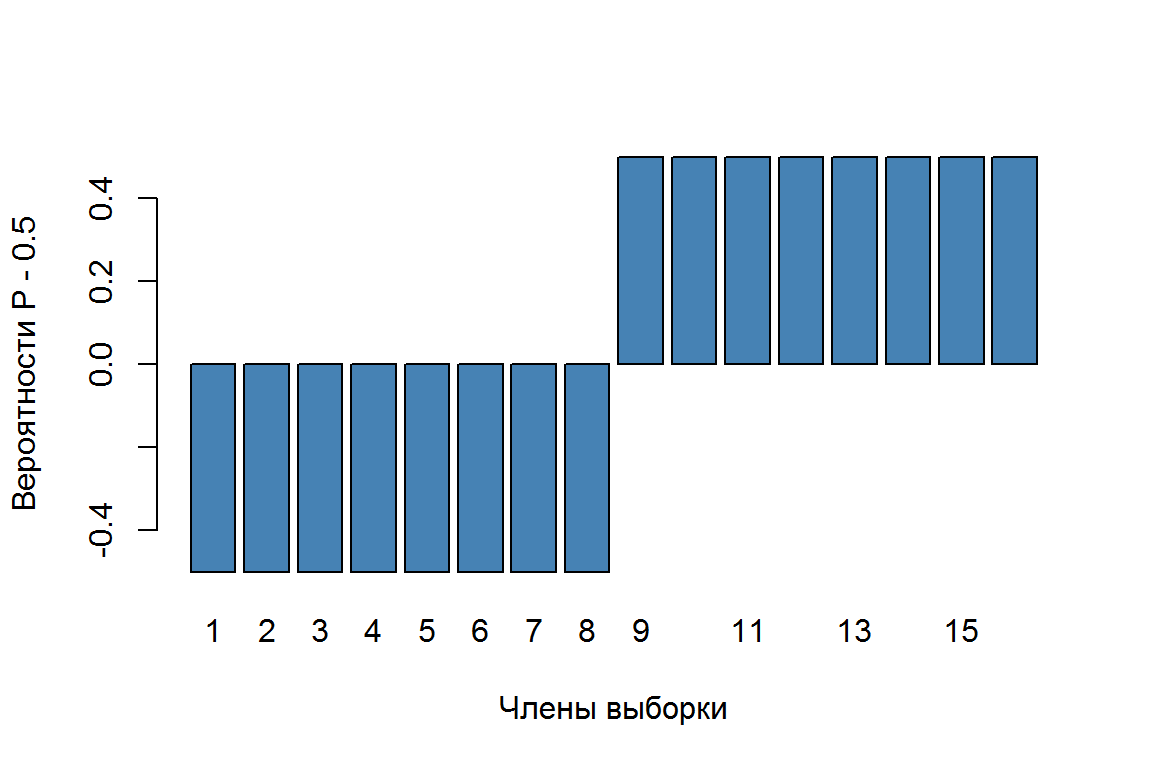
Рисунок 5.2: Диаграмма вероятностей, предсказанных логит-регрессией
Все члены обучающей выборки с использованием полученной регрессионной модели были верно классифицированы и с максимальной вероятностью (см. рис. 5.2). Перекрестную проверку построенной модели можно выполнить, например, с использованием функции cv.glm() из пакета boot. Если параметр K, определяющий число блоков разбиения, опущен, то выполняется скользящий контроль:
library(boot)
cv.glm(DFace, logit.step)$delta## [1] 2.564444e-17 2.404152e-17В результате получены среднеквадратичное отклонение по координате логита от проверочных наблюдений до гиперплоскости, найденной на обучающих выборках, а также его скорректированное значение (adjusted cross-validation estimate of prediction error). Поскольку ошибки перекрестной проверки ничтожно малы и все объекты в ее ходе были правильно опознаны, то в целом полученную модель можно считать высоко эффективной.
Мы убедились в том, что логистическая регрессия и функция glm() отлично работают с индикаторными переменными. Однако строгие аналитики (Дюк, Самойленко, 2001) считают, что “вряд ли такое правило способно удовлетворить разработчика интеллектуальной системы. Оно формально, не дает нового знания, а попытка дать интерпретацию коэффициентам регрессии приводит к сомнительным выводам. Непонятно, например, почему вес формы носа (х3) в два раза превышает вес оттопыренности ушей (х2) и т.д.” Несмотря на высказанные сомнения, мы достигли желаемой цели - достоверное и эффективное правило классификации построено, а из анализа коэффициентов модели легко сделать вывод, что признаки x3, x4, x5 и x14 склонны иметь демократы, а показатели x2, x7 и x13 характеризуют патриотические устремления.
Рассмотрим теперь результаты стандартного линейного дискриминантного анализа, не вдаваясь в его исходные статистические предпосылки, смысл и технику вычислений (это будет подробно обсуждаться в следующих главах):
library("MASS")
Fac.lda <- lda(DFace[,1:16], grouping = DFace$Class)
pred <- predict(Fac.lda, DFace[, 1:16])
table(Факт = DFace$Class, Прогноз = pred$class)## Прогноз
## Факт 1 2
## 1 6 2
## 2 2 6Acc = mean(DFace$Class == pred$class)
paste("Точность=", round(100*Acc, 2), "%", sep="")## [1] "Точность=75%"Обратим внимание на неприятное сообщение о коллинеарности переменных и мало впечатляющие результаты прогноза.
Стохастические модели многомерных двоичных случайных величин основываются на распределении Бернулли \(\mathbf{X} = \{ x_1, \dots, x_m \} = \text{Be}_m(\boldsymbol{\mu}, \zeta)\), где \(\boldsymbol{\mu}\) - вектор математических ожиданий, а \(\zeta\) включает \((2^m - m - 1)\) параметров, оценивающих взаимодействие между переменными \(x_j\). Как и в одномерном случае, дисперсии полностью определяются через средние \(\text{Var}(x_j) = \mu_j(1-\mu_j)\).
Во многих случаях, особенно для предсказания на основе выборок малого объема, но с большим числом предикторов, представляется разумным следовать “наивному” байесовскому подходу, т.е. игнорировать зависимости между индивидуальными переменными \(x_j\). Тогда количество параметров многомерной модели Бернулли существенно сокращается и функция объединенной плотности вероятности определяется произведением \(\mu_j\) и диагональной ковариационной матрицей \(\text{Var}(x_j) = \text{diag}[\mu_j(1-\mu_j)]\).
С учетом этих положений разработан метод бинарного дискриминантного анализа (binDA - binary discriminant analysis; Gibb, Strimmer, 2015). Дискриминантная функция, полученная на основе теоремы Байеса, для каждого класса с меткой y имеет следующий вид:
\[d_y(x) = \log \pi_y + \log(P(\boldsymbol{x}|y)) + C,\]
где \(\pi_y\) - априорная вероятность класса \(y\), \(C\) - константа, а совокупная условная вероятность предикторов в зависимости от значения отклика вычисляется по формуле
\[ P(\boldsymbol{x}|y)=\prod_{i=1}^m \begin{cases} 1-\mu_{yj}, \quad \text{если} \, \, x_j = 0\\ \mu_{yj}, \quad \text{если} \, \, x_j = 1 \end{cases} \]
Тестируемый объект относится к тому классу \(y\), дискриминантная функция которого \(d_y(x)\) максимальна. Параметром алгоритма является \(\lambda\) - степень ослабления дисбаланса в частотах классов (lambda.freqs - shrinkage intensity for the frequencies). При lambda.freqs = 0 используются эмпирические частоты классов \(\pi_y= n_y/n\), а при lambda.freqs = 1 все вероятности принимаются равными.
Важным разделом алгоритма является устранение подмножества предикторов, влияние которых на значение метки y статистически незначимо. Разность между значениями логарифма функции правдоподобия полной модели и нуль-модели без параметров равна относительной энтропии, или дивергенции \(D\) Кульбака-Лейблера (Kullback-Leibler). Относительные вклады \(S_j\) каждого индивидуального предиктора в величину \(D\) определяют меру значимости \(j\)-й переменной в результате классификации. Отсюда легко найти матрицу \(t\)-значений, соответствующих разностям между общим средним и средними для каждой переменной относительно каждого класса.
Алгоритм binDA реализован в пакете binda для R. Выполним построение дискриминантной модели и оценим точность прогнозирования на обучающей выборке:
library(binda)
Xtrain <- as.matrix(DFace[, 1:16])
is.binaryMatrix(Xtrain) # Проверяем бинарность матрицы## [1] TRUEClass = as.factor(DFace$Class)
binda.fit = binda(Xtrain, Class, lambda.freq = 1)## Number of variables: 16
## Number of observations: 16
## Number of classes: 2
##
## Specified shrinkage intensity lambda.freq (frequencies): 1pred <- predict(binda.fit, Xtrain)## Prediction uses 16 features.table(Факт = DFace$Class, Прогноз = pred$class)## Прогноз
## Факт 1 2
## 1 8 0
## 2 2 6Acc = mean(DFace$Class!= pred$class)
paste("Точность=", round(100*Acc, 2), "%", sep="")## [1] "Точность=12.5%"При равных апостериорных вероятностях классов 0.5/0.5 объект №4 был ошибочно отнесен ко второму классу.
Выполним теперь оценку информативности предикторов по \(t\)-критерию (рис. 3.3):
# ранжируем предикторы
binda.x <- binda.ranking(Xtrain, Class)## Number of variables: 16
## Number of observations: 16
## Number of classes: 2
##
## Estimating optimal shrinkage intensity lambda.freq (frequencies): 1plot(binda.x, top = 40, arrow.col = "blue",
zeroaxis.col = "red", ylab = "Предикторы", main = "")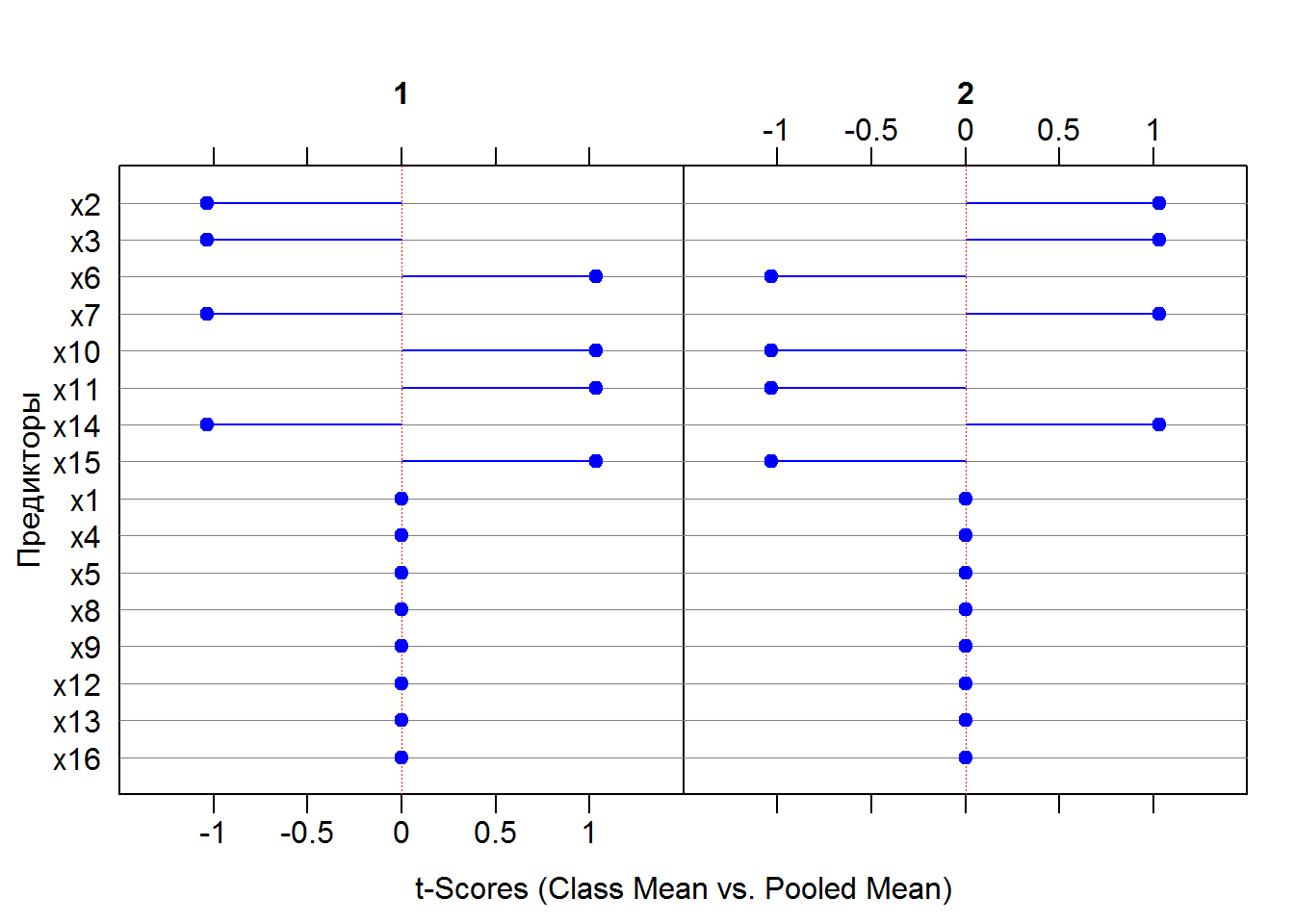
Рисунок 5.3: Диаграмма вероятностей, предсказанных логит-регрессией
Все переменные разделились на две группы: значимые для классификации (x2, x3, x6, x7, x10, x11, x14, x15) со значением \(t = \pm 1.032\) и незначимые (x1, x4, x5, x8, x9, x12, x13, x16) с \(t = 0\). Интересно сравнить этот список со списком информативных предикторов, полученных пошаговой процедурой логистической регрессии.
К сожалению, использование функции train() из пакета caret как с параметрами method = "glm", family = binomial, так и method = "binda" привело к неудаче. Видимо, при \(n\) = 16 еще не достигнут порог репрезентативности исходных данных, при котором эта функция начинает стабильно выдавать адекватные результаты.
library(caret)
binda.train <- train(Xtrain, Class, method = "binda", verbose = FALSE)library(caret)
binda.train <- train(Xtrain, Class, method = "binda", verbose = FALSE)
binda.trainОтрицательная величина Kappa практически означает, что тестируемый классификатор хуже случайного угадывания. Однако итоговая модель подобных неожиданностей не несет:
pred.train <- predict(binda.train, Xtrain)## Prediction uses 16 features.(CTab <- table(Факт = DFace$Class, Прогноз = pred.train))## Прогноз
## Факт 1 2
## 1 7 1
## 2 2 6Acc = mean(DFace$Class == pred.train)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=81.25%"