6.3 Ядерные функции машины опорных векторов
При наличии нелинейной связи между признаками и откликом качество линейных классификаторов, как показано на рис. 6.4, часто может оказаться неудовлетворительным. Для учета нелинейности обычно расширяют пространство переменных, включая различные функциональные преобразования исходных предикторов (полиномы, экспоненты и проч.). Машину опорных векторов SVM (Support Vector Machine) можно рассматривать как нелинейное обобщение линейного классификатора, представленного в разделе 6.2, основанное на расширении размерности исходного пространства предикторов с помощью специальных ядерных функций. Это позволяет строить модели с использованием разделяющих поверхностей самой различной формы.
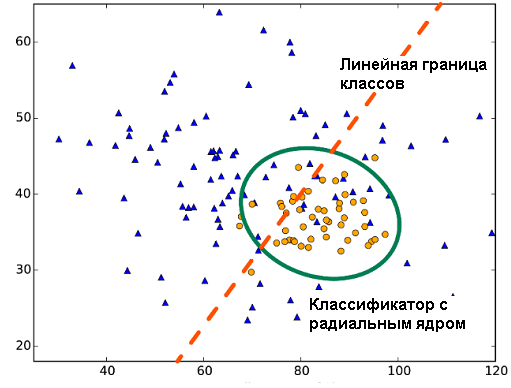
Рисунок 6.4: Линейная и радиальная границы классов
Собственно ядром является любая симметричная, положительно полуопределенная матрица \(\mathbf{K}\), которая составлена из скалярных произведений пар векторов \(\boldsymbol{x}_i\) и \(\boldsymbol{x}_j\): \(K(\boldsymbol{x}_i, \boldsymbol{x}_j) = \langle\phi(\boldsymbol{x}_i), \phi(\boldsymbol{x}_j)\rangle\) характеризующих меру их близости. Здесь \(\phi\) - произвольная преобразующая функция, формирующая ядро. В качестве таких функций чаще всего используют следующие:
- линейное ядро: \(K(\boldsymbol{x}_i, \boldsymbol{x}_j) = \boldsymbol{x}_i^T \boldsymbol{x}_j\), что соответствует классификатору на опорных векторах в исходном пространстве (см. рис. 6.3);
- полиномиальное ядро со степенью \(p\): \(K(\boldsymbol{x}_i, \boldsymbol{x}_j) = (1 + \boldsymbol{x}_i^T \boldsymbol{x}_j)^p\);
- гауссово ядро с радиальной базовой функцией (RBF): \(K(\boldsymbol{x}_i, \boldsymbol{x}_j) = \exp(\gamma||\boldsymbol{x}_i - \boldsymbol{x}_j||^2)\);
- сигмодиное ядро: \(K(\boldsymbol{x}_i, \boldsymbol{x}_j) = \tanh(\gamma \boldsymbol{x}_i^T \boldsymbol{x}_j +\beta_0 )\).
Каждое ядро характеризуется параметрами (\(p, \gamma, \beta_0\) и т.д.), которые подлежат оптимизации.
Основная идея использования ядер заключается в том, что при отображении данных в пространство более высокой размерности исходное множество точек может стать линейно разделимым (Cristianini, Shawe-Taylor, 2000). Тогда естественно предположить, что оптимальная разделяющая гиперплоскость машины опорных векторов может быть найдена путем подбора коэффициентов \(\alpha_i\) выражения \(\sum_{i=1}^p \alpha_i K(x, x_i) + \beta_0\). Таким образом, как и в линейном случае, решается математически удобная задача квадратичной оптимизации с использованием множителей Лагранжа. Вычисление экстремума в расширенных пространствах столь огромных размерностей оказалось также возможным потому, что ядро формируется только для ограниченного набора опорных векторов.
Построение классификатора на опорных векторах с использованием перечисленных выше ядер можно осуществить с помощью знакомой нам функции svm() из пакета e1071. Отметим, что по умолчанию в этой функции установлено значение параметра kernel = "radial", т.е. принято RBF-ядро.
Для подгонки модели распознавания типа стекла (разделы 6.1-6.2) нам необходимо предварительно оценить значения двух параметров: \(C\) (cost) - допустимый штраф за нарушение границы зазора и \(\gamma\) (gamma) - параметр радиальной функции. При увеличении С происходит уменьшение зазора и количества используемых опорных векторов: граница между классами становится более извилистой, а классификатор более точным на обучающей выборке и менее точным - на контрольной выборке. В состав пакета входит функция tune.svm(), которая по информации о строящейся модели и с использованием перекрестной проверки осуществляет предварительный отбор необходимых параметров:
DGlass <- read.table(file = "data/Glass.txt", sep = ",",
header = TRUE, row.names = 1)
DGlass$FAC <- as.factor(ifelse(DGlass$Class == 2, "C2", "C1"))
library(e1071)
tune.svm(FAC ~ ., data = DGlass[, -10], gamma = 2^(-1:1),
cost = 2^(2:4))##
## Parameter tuning of 'svm':
##
## - sampling method: 10-fold cross validation
##
## - best parameters:
## gamma cost
## 0.5 4
##
## - best performance: 0.1786765svm.rbf <- svm(formula = FAC ~ ., data = DGlass[, -10],
kernel = "radial", cost = 4, gamma = 0.5)
(table(Факт = DGlass$FAC, Прогноз = predict(svm.rbf)))## Прогноз
## Факт C1 C2
## C1 85 2
## C2 7 69Acc <- mean(predict(svm.rbf) == DGlass$FAC)
paste("Точность=", round(100*Acc, 2), "%", sep = "") ## [1] "Точность=94.48%"Мы получили классификатор, значительно превышающий по точности рассмотренные выше модели линейного дискриминантного анализа и опорных векторов с линейным ядром. Полученная разделяющая поверхность имеет многомерный характер, но мы можем оценить ее внешний вид, создавая двумерные проекции любых двух исходных переменных из 9 (например, концентрации алюминия и магния):
svm2.rbf <- svm(formula = FAC ~ Al + Mg, data = DGlass[, -10],
kernel = "radial", cost = 4, gamma = 2.5)
Acc <- mean(predict(svm2.rbf) == DGlass$FAC)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=85.89%"plot(svm2.rbf, DGlass[, c(3,4,11)],
svSymbol = 16, dataSymbol = 2, color.palette = terrain.colors)
legend("bottomleft", c("Опорные кл.1", "Опорные кл.2",
"Данные кл.1", "Данные кл.2"),
col = c(1,2,1,2), pch = c(16, 16, 2, 2))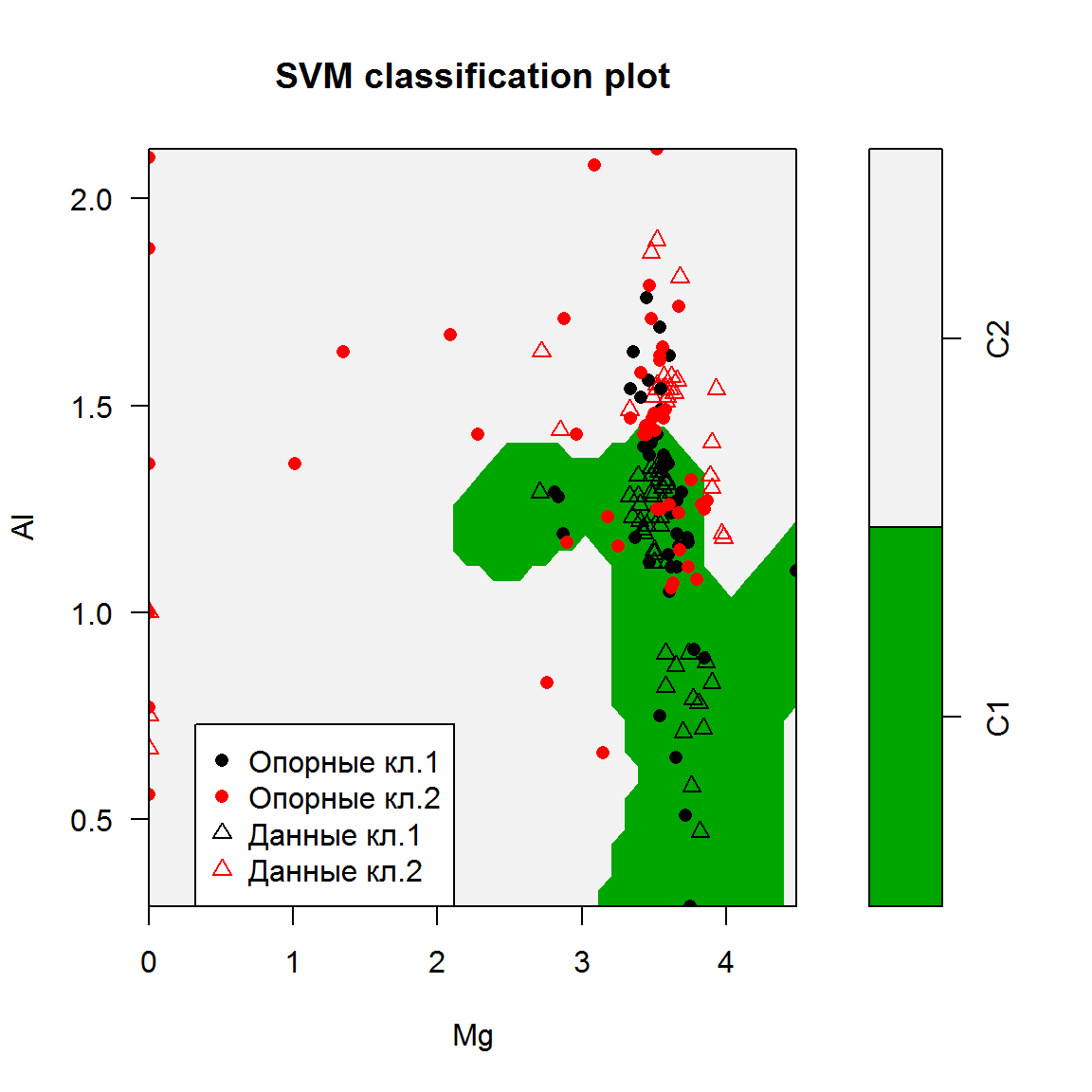
Рисунок 6.5: Пример классификатора на опорных векторах с использованием в качестве ядра радиальной базисной функции
Выполним аналогичные действия с использованием функции train() из пакета caret, где для построения модели опорных векторов используется функция svm() из пакета kernlab. Здесь также осуществляется подбор двух параметров - C и sigma (вероятно, то же самое, что и gamma). Определим диапазоны их варьирования в таблице grid: C - от 2 до 5, а sigma - от 0.3 до 0.6:
ctrl <- trainControl(method = "repeatedcv", repeats = 5,
summaryFunction = twoClassSummary, classProbs = TRUE)
grid <- expand.grid(sigma = (3:6)/10, C = 2:5)
set.seed(101)
(svmRad.tune <- train(DGlass[, 1:9], DGlass$FAC,
method = "svmRadial", metric = "ROC",
tuneGrid = grid, trControl = ctrl))## Support Vector Machines with Radial Basis Function Kernel
##
## 163 samples
## 9 predictor
## 2 classes: 'C1', 'C2'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times)
## Summary of sample sizes: 146, 146, 146, 146, 147, 146, ...
## Resampling results across tuning parameters:
##
## sigma C ROC Sens Spec
## 0.3 2 0.8706647 0.8111111 0.7935714
## 0.3 3 0.8697173 0.8158333 0.7985714
## 0.3 4 0.8678075 0.8219444 0.7967857
## 0.3 5 0.8659077 0.8336111 0.8017857
## 0.4 2 0.8734921 0.8019444 0.8146429
## 0.4 3 0.8698810 0.8150000 0.8225000
## 0.4 4 0.8655456 0.8219444 0.8135714
## 0.4 5 0.8604415 0.8238889 0.8139286
## 0.5 2 0.8738194 0.8041667 0.8196429
## 0.5 3 0.8634821 0.8080556 0.8114286
## 0.5 4 0.8529861 0.8008333 0.8089286
## 0.5 5 0.8427827 0.7961111 0.8035714
## 0.6 2 0.8704117 0.7941667 0.8167857
## 0.6 3 0.8531498 0.7872222 0.8089286
## 0.6 4 0.8466716 0.7872222 0.8010714
## 0.6 5 0.8370635 0.7777778 0.8060714
##
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were sigma = 0.5 and C = 2.pred <- predict(svmRad.tune,DGlass[, 1:9])
(table(Факт = DGlass$FAC, Прогноз = pred))## Прогноз
## Факт C1 C2
## C1 84 3
## C2 7 69Acc <- mean(pred == DGlass$FAC)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=93.87%"При рассмотрении приведенного примера (рис. 6.5) может создаться впечатление, что полученные нелинейные плоскости хорошо зарекомендовали себя при предсказании, но трудно интерпретируемы с точки зрения объяснения. Так и есть. Однако основная задача подобных моделей - научиться распознавать образы (pattern recognition), что нашло широкое применение в вычислительной биологии, генетике, спектроскопии, анализе данных, полученных с использованием микрочипов (microarray) и т.д.
Большие возможности использования разнообразных ядерных функций представлены в пакете kernlab. Рассмотрим пример, представленный в документации к пакету и связанный с задачей распознавания двух вложенных друг в друга спиралей:
library(kernlab)
library(ggplot2)
set.seed(2335246L)
data(spirals)
# Спектральная функция выделяет две различные спирали
sc <- specc(spirals, centers = 2)
s <- data.frame(x = spirals[, 1], y = spirals[, 2],
class = as.factor(sc))
# Данные делятся на обучающую и проверочную выборки:
s$group <- sample.int(100, size = dim(s)[[1]], replace = TRUE)
sTrain <- subset(s, group > 10)
sTest <- subset(s, group <= 10)
# Снова используем Гауссово или радиальное ядро:
mSVMG <- ksvm(class ~ x + y, data = sTrain, kernel = 'rbfdot')
sTest$predSVMG <- predict(mSVMG, newdata = sTest,type = 'response')
table(Факт = sTest$class, Прогноз = sTest$predSVMG) ## Прогноз
## Факт 1 2
## 1 20 0
## 2 0 22ggplot() +
geom_text(data = sTest, aes(x = x, y = y,
label = predSVMG), size = 12) +
geom_text(data = s, aes(x = x, y = y,
label = class, color = class), alpha = 0.7) +
coord_fixed() +
theme_bw() + theme(legend.position = 'none') 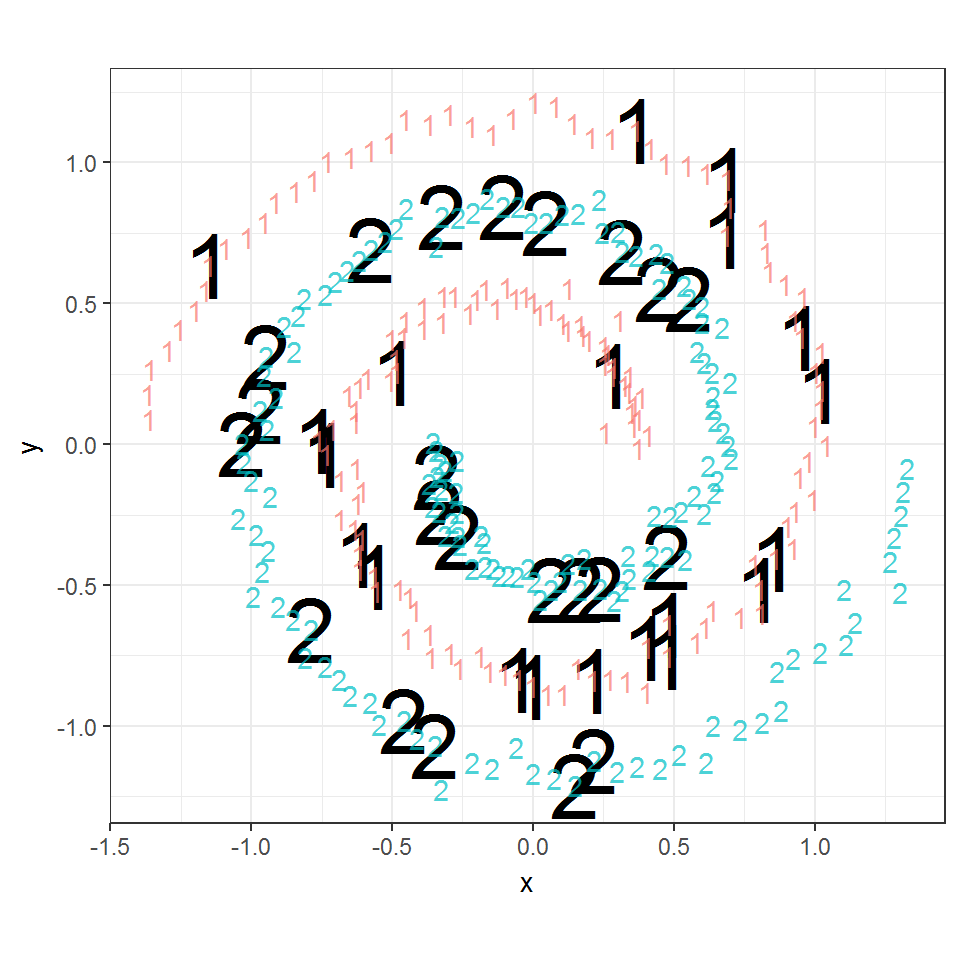
Рисунок 6.6: Использование радиального ядра для разделения двух вложенных спиралей
В результате использования радиальной ядерной функции была построена разделяющая поверхность между двумя вложенными спиралями таким образом, что ошибочное предсказание правильного класса наблюдалось лишь для 3 объектов проверочной выборки из 29 (рис. 6.6).