8.5 ZIP- и барьерные модели счетных данных
Как обсуждалось выше, реальные данные часто характеризуются существенными отклонениями от теоретического однопараметрического распределения Пуассона: избытком нулевых значений и/или нарушениями предположения о параметре дисперсии \(\text{Var}(Y) \neq E(Y)\). Учесть повышенную разреженность данных можно с использованием модели Пуассона со смешанными параметрами, учитывающей избыток нулей (Zero Inflated Poisson, ZIP), или специальной двухкомпонентной модели с измененными нулями (Zero-altered Poisson, ZAP), которую часто называют “барьерной” моделью (hurdle model). Если наряду с избытком нулей имеет место отчетливая избыточная дисперсия, то можно воспользоваться соответствующими моделями на основе отрицательного биномиального распределения: ZINB (Zero-inflated Negative Binomial) и ZANB (Zero-altered Negative Binomial). Эти четыре модели будут предметом нашего дальнейшего обсуждения (подробности см. в Zeileis et al., 2008; Zuur et al., 2009; Cameron, Trivedi, 2013; Кшнясев, 2010).
Рассмотрим в качестве примера таблицу NMES1988 из пакета AER, содержащий данные о визитах 4406 респондентов старше 66 лет в учреждения бесплатного медицинского обслуживания США в 1988 г. Число посещений visits примем в качестве отклика, а три метрических переменных и три фактора используем в качестве предикторов:
library(AER)
data("NMES1988") # Загружаем данные и отбираем столбцы
nmes <- NMES1988[, c(1, 6:8, 13, 15, 18)]
sum(nmes$visits < 1) # наблюдаемое число нулей## [1] 683plot(table(nmes$visits)) 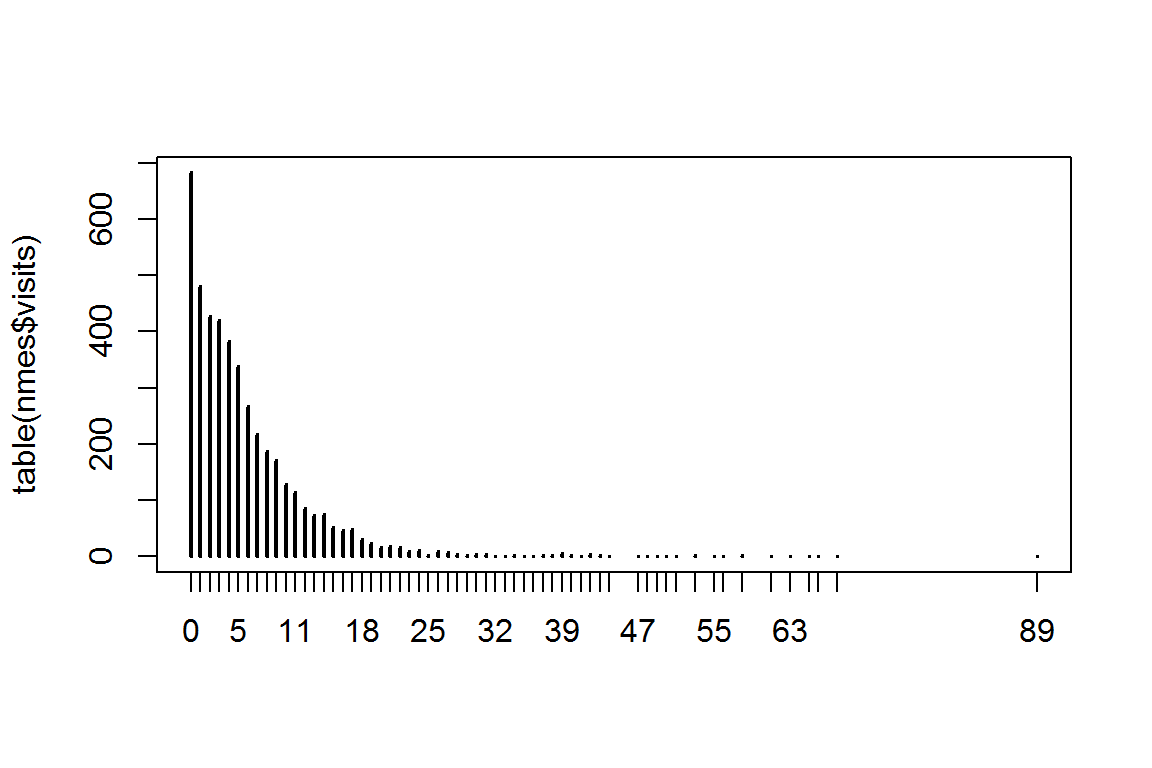
Рисунок 8.9: Наблюдаемые частоты посещений врача
Вычислим теоретическую частоту нулевых значений:
mod1 <- glm(visits ~ ., data = nmes, family = "poisson")
mu <- predict(mod1, type = "response") # среднее Пуассона
exp <- sum(dpois(x = 0, lambda = mu)) # теоретическая частота
round(exp) # нулевых значений## [1] 47Модели ZIP и ZINB называют моделями со смешанными параметрами (mixture models), поскольку присутствие нулей считается итогом двух различных процессов: биномиального процесса и процесса формирования счетной случайной величины. Здесь биномиальный процесс моделирует вероятность измерения ложно-положительного результата против всех других типов данных (включая истинные нули и конкретные счетные значения). Иными словами, мы делим данные на три воображаемые группы: первая группа содержит только ложные нули – наблюдения с вероятностью появления \(\pi_i\), вторая группа - истинные нули с вероятностью \((pi_i - 1)\), и третья группа - ненулевые наблюдения, которые (вместе со второй группой!) моделируются регрессией Пуассона с учетом независимых переменных. Тогда распределение вероятностей по ZIP-модели определяется следующими выражениями:
\[P(y_i = 0) = \pi_i + (1 + \pi_i) \times e^{-\mu_i}, \, \, \, \mu_i = e^{\alpha + \beta_1 x_{1i} + \beta_2 x_{2i} + \dots}\]
\[P(Y_i = y_i | y_i > 0) = (1 - \pi_i) \times \frac{\mu^{y_i} \times e^{-\mu_i}}{y_i!}, \, \, \, \pi_i = \frac{e^{\nu}}{1 + e^{\nu}}.\]
Модель ZINB формулируется так же, но значение \(\mu_i\) подгоняется с использованием отрицательного биномиального распределения.
Построение моделей с избыточными нулями осуществляется с использованием функции zeroinfl() из пакета pscl, для чего необходимо выполнить следующий код:
library(pscl)
M.ZIP <- zeroinfl(visits ~ ., data = nmes, dist = "poisson", link = "logit")
summary(M.ZIP)##
## Call:
## zeroinfl(formula = visits ~ ., data = nmes, dist = "poisson", link = "logit")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -5.4092 -1.1579 -0.4769 0.5435 25.0380
##
## Count model coefficients (poisson with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.405812 0.024175 58.152 < 2e-16 ***
## hospital 0.159011 0.006060 26.239 < 2e-16 ***
## healthpoor 0.253454 0.017705 14.315 < 2e-16 ***
## healthexcellent -0.304134 0.031151 -9.763 < 2e-16 ***
## chronic 0.101836 0.004721 21.571 < 2e-16 ***
## gendermale -0.062332 0.013054 -4.775 1.80e-06 ***
## school 0.019144 0.001873 10.221 < 2e-16 ***
## insuranceyes 0.080557 0.017145 4.699 2.62e-06 ***
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.08102 0.14233 -0.569 0.569219
## hospital -0.30330 0.09158 -3.312 0.000927 ***
## healthpoor 0.02166 0.16170 0.134 0.893431
## healthexcellent 0.23786 0.14990 1.587 0.112550
## chronic -0.53117 0.04601 -11.545 < 2e-16 ***
## gendermale 0.41527 0.08919 4.656 3.22e-06 ***
## school -0.05677 0.01223 -4.640 3.49e-06 ***
## insuranceyes -0.75294 0.10257 -7.341 2.12e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Number of iterations in BFGS optimization: 24
## Log-likelihood: -1.613e+04 on 16 DfПостроенная модель ZIP включает следующие статистически значимые переменные: время пребывания в больнице (hospital), оценка хроничности заболевания (chronic), длительности обучения (school), пола (gender), наличия страховки (insurance). Самооценка же здоровья (health) оказалась незначимой.
Аналогичным образом можно построить модель с использованием отрицательного биномиального распределения, которая имеет аналогичную структуру и поэтому полный протокол результатов не приводится:
M.ZINB <- zeroinfl(visits ~ ., data = nmes, dist = "negbin", link = "logit")
summary(M.ZINB) ##
## Call:
## zeroinfl(formula = visits ~ ., data = nmes, dist = "negbin", link = "logit")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -1.1966 -0.7097 -0.2784 0.3256 17.7661
##
## Count model coefficients (negbin with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.193466 0.056737 21.035 < 2e-16 ***
## hospital 0.201214 0.020392 9.867 < 2e-16 ***
## healthpoor 0.287190 0.045940 6.251 4.07e-10 ***
## healthexcellent -0.313540 0.062977 -4.979 6.40e-07 ***
## chronic 0.128955 0.011938 10.802 < 2e-16 ***
## gendermale -0.080093 0.031035 -2.581 0.00986 **
## school 0.021338 0.004368 4.886 1.03e-06 ***
## insuranceyes 0.126815 0.041687 3.042 0.00235 **
## Log(theta) 0.394731 0.035145 11.231 < 2e-16 ***
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.06354 0.27668 -0.230 0.81837
## hospital -0.81760 0.43875 -1.863 0.06240 .
## healthpoor 0.10178 0.44071 0.231 0.81735
## healthexcellent 0.10488 0.30965 0.339 0.73484
## chronic -1.24630 0.17918 -6.956 3.51e-12 ***
## gendermale 0.64937 0.20046 3.239 0.00120 **
## school -0.08481 0.02676 -3.169 0.00153 **
## insuranceyes -1.15808 0.22436 -5.162 2.45e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Theta = 1.484
## Number of iterations in BFGS optimization: 31
## Log-likelihood: -1.209e+04 on 17 DfВизуально сравнить степень согласия эмпирических и оцененных моделью частот можно с использованием гистограмм (поскольку для лучшего восприятия графика из частот извлекают квадратный корень, их называют еще “рутограммами” - от англ. “root”, корень):
# для инсталляции countreg выполните команду:
# install.packages("countreg", repos="http://R-Forge.R-project.org")
library(countreg)
rootogram(M.ZIP)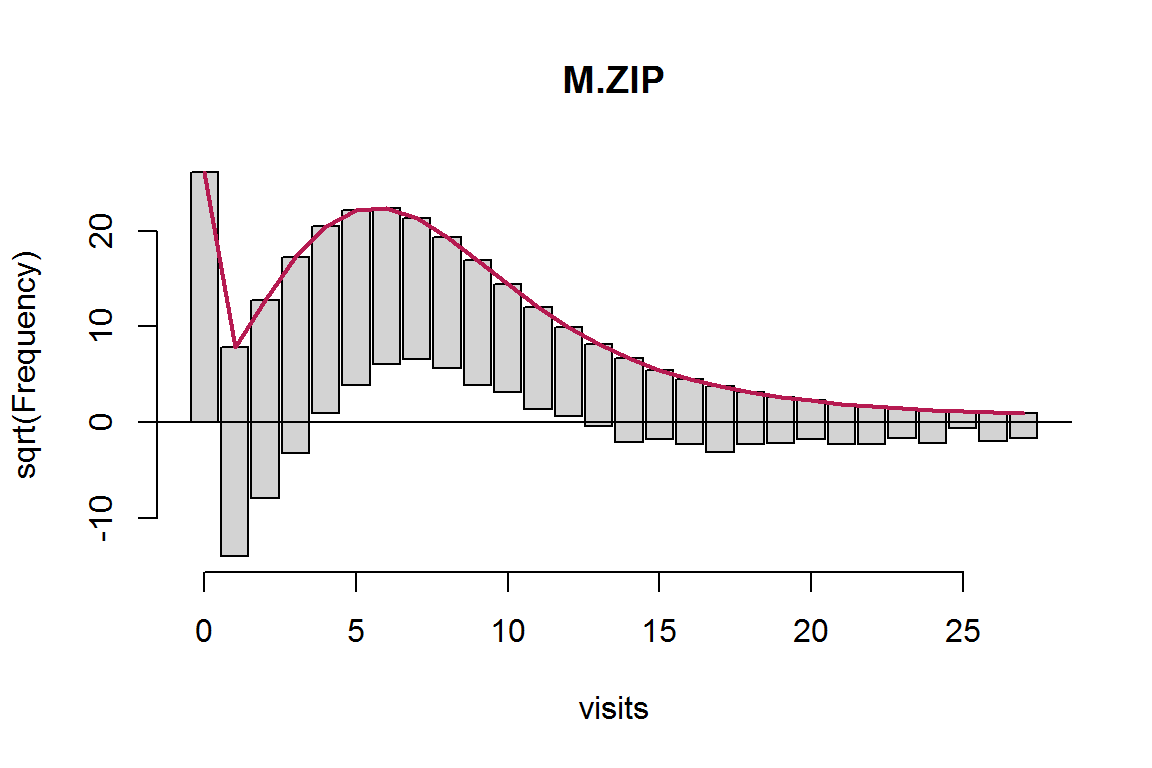
Рисунок 8.10: Рутограмма частот для модели ZIP
rootogram(M.ZINB)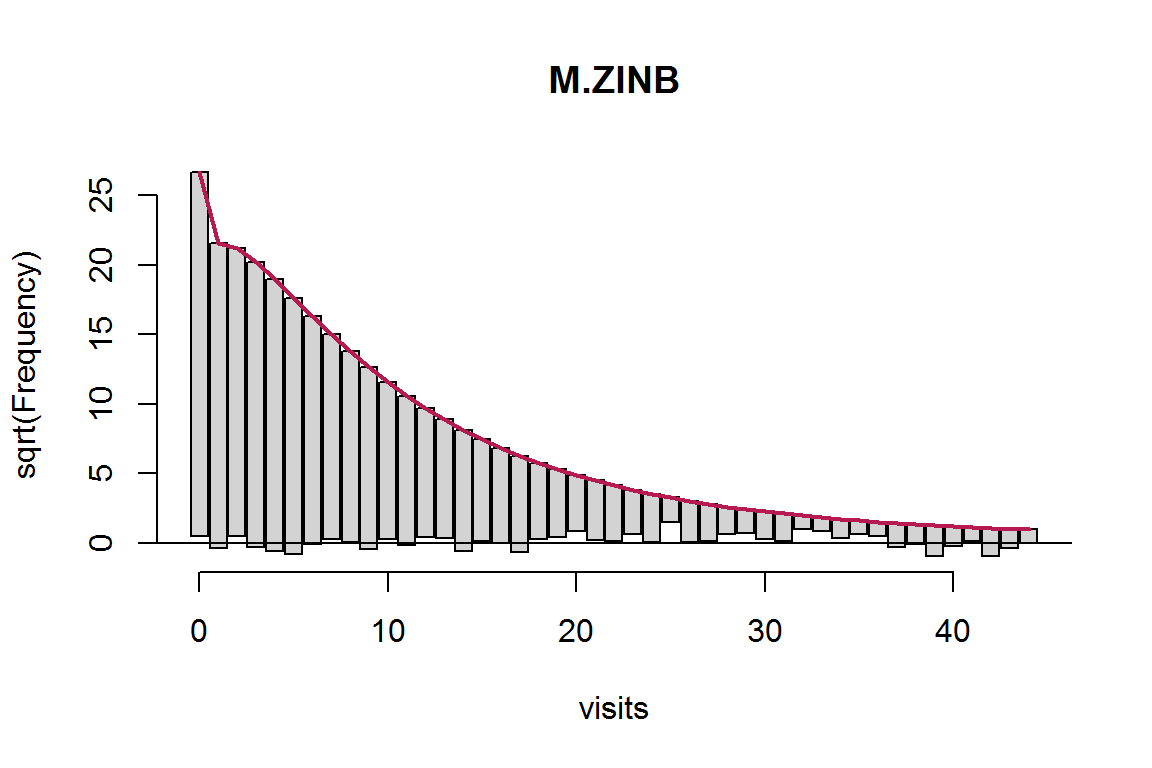
Рисунок 8.11: Рутограмма частот для модели ZINB
В результате введения в модель на основе отрицательного биномиального распределения ZINB дополнительного параметра Theta, компенсирующего избыточную дисперсию, оценки коэффициентов и их уровней значимостей были уточнены, максимум логарифма функции правдоподобия увеличился, а гистограмма на рис. 8.11 приобрела более плавный характер.
Заметим, что мы построили простейший вариант моделей, исходя из предположения о том, что параметр \(\pi_i\) равен постоянному значению (т.е. \(\nu = const\)). Изменяя структуру правой части объекта formula, мы можем задать любую зависимость для от имеющихся ковариат (Zuur et al., 2009)
Барьерная модель по своему смыслу является уже не смешанной, а двухкомпонентной моделью, т.е. задается как комбинация двух самостоятельных уравнений регрессии: логит-регрессии для моделирования вероятности \(P(y_i = 0)\) на основе биномиального распределения, и множественной регрессии для ненулевой средней численности в предположении одно- или двухпараметрического распределения для стохастической компоненты, например:
\[ f_{ZAP}(y; \beta, \gamma) = \begin{cases} f_{bin}(y = 0; \gamma) & \quad \text{для } y=0\\ (1-f_{bin}(y = 0; \gamma))\times\frac{f_{Pois}(y;\beta)}{1-f_{Pois}(y;\beta)} & \quad \text{для } y>0\\ \end{cases}. \]
Выполним построение моделей ZAP и ZANB, для чего воспользуемся функцией hurdle() из пакета pscl:
M.ZAP <- hurdle(visits ~ ., data = nmes,
dist = "poisson", zero.dist = "binomial", link = "logit")
summary(M.ZAP)##
## Call:
## hurdle(formula = visits ~ ., data = nmes, dist = "poisson", zero.dist = "binomial",
## link = "logit")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -5.4144 -1.1565 -0.4770 0.5432 25.0228
##
## Count model coefficients (truncated poisson with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.406459 0.024180 58.167 < 2e-16 ***
## hospital 0.158967 0.006061 26.228 < 2e-16 ***
## healthpoor 0.253521 0.017708 14.317 < 2e-16 ***
## healthexcellent -0.303677 0.031150 -9.749 < 2e-16 ***
## chronic 0.101720 0.004719 21.557 < 2e-16 ***
## gendermale -0.062247 0.013055 -4.768 1.86e-06 ***
## school 0.019078 0.001872 10.194 < 2e-16 ***
## insuranceyes 0.080879 0.017139 4.719 2.37e-06 ***
## Zero hurdle model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.043147 0.139852 0.309 0.757688
## hospital 0.312449 0.091437 3.417 0.000633 ***
## healthpoor -0.008716 0.161024 -0.054 0.956833
## healthexcellent -0.289570 0.142682 -2.029 0.042409 *
## chronic 0.535213 0.045378 11.794 < 2e-16 ***
## gendermale -0.415658 0.087608 -4.745 2.09e-06 ***
## school 0.058541 0.011989 4.883 1.05e-06 ***
## insuranceyes 0.747120 0.100880 7.406 1.30e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Number of iterations in BFGS optimization: 14
## Log-likelihood: -1.613e+04 on 16 DfM.ZANB <- hurdle (visits ~ ., data = nmes,
dist = "negbin", link="logit")
summary(M.ZANB)##
## Call:
## hurdle(formula = visits ~ ., data = nmes, dist = "negbin", link = "logit")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -1.1718 -0.7080 -0.2737 0.3196 18.0092
##
## Count model coefficients (truncated negbin with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.197699 0.058973 20.309 < 2e-16 ***
## hospital 0.211898 0.021396 9.904 < 2e-16 ***
## healthpoor 0.315958 0.048056 6.575 4.87e-11 ***
## healthexcellent -0.331861 0.066093 -5.021 5.14e-07 ***
## chronic 0.126421 0.012452 10.152 < 2e-16 ***
## gendermale -0.068317 0.032416 -2.108 0.0351 *
## school 0.020693 0.004535 4.563 5.04e-06 ***
## insuranceyes 0.100172 0.042619 2.350 0.0188 *
## Log(theta) 0.333255 0.042754 7.795 6.46e-15 ***
## Zero hurdle model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.043147 0.139852 0.309 0.757688
## hospital 0.312449 0.091437 3.417 0.000633 ***
## healthpoor -0.008716 0.161024 -0.054 0.956833
## healthexcellent -0.289570 0.142682 -2.029 0.042409 *
## chronic 0.535213 0.045378 11.794 < 2e-16 ***
## gendermale -0.415658 0.087608 -4.745 2.09e-06 ***
## school 0.058541 0.011989 4.883 1.05e-06 ***
## insuranceyes 0.747120 0.100880 7.406 1.30e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Theta: count = 1.3955
## Number of iterations in BFGS optimization: 16
## Log-likelihood: -1.209e+04 on 17 Dfpar(mfrow = c(1, 2))
rootogram(M.ZAP)
rootogram(M.ZANB)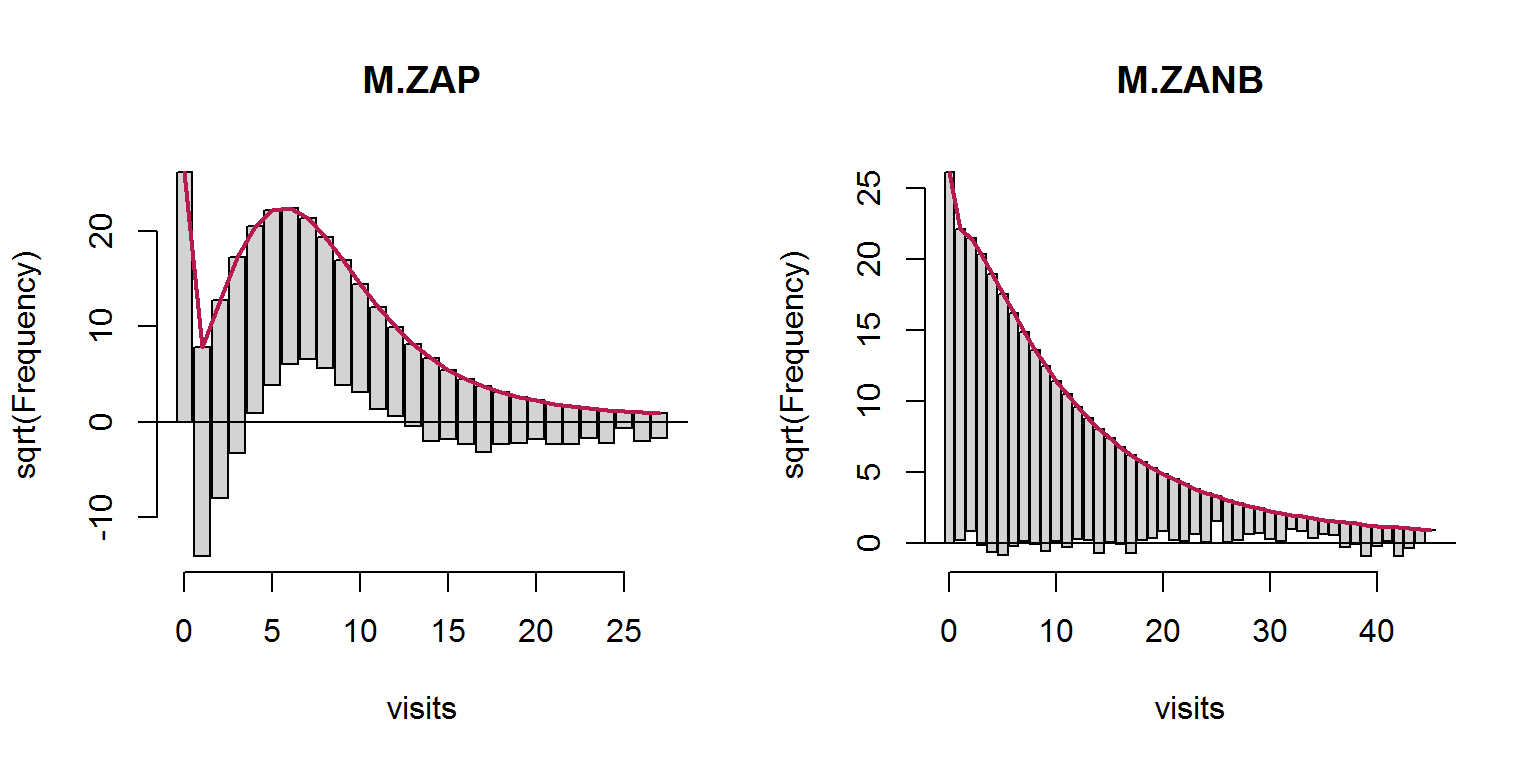
Рисунок 8.12: Рутограмма частот моделей ZAP и ZANB
На вопрос о том, какая модель эффективнее, можно дать очевидный ответ (M.ZANB):
fm <- list("ZIP" = M.ZIP, "ZINB" = M.ZINB,
"Hurdle-Pois" = M.ZAP, "Hurdle-NB" = M.ZANB)
rbind(logLik = sapply(fm, function(x) round(logLik(x), digits = 0)),
AIC = sapply(fm, function(x) round(AIC(x), digits = 0)))## ZIP ZINB Hurdle-Pois Hurdle-NB
## logLik -16134 -12091 -16134 -12088
## AIC 32300 24215 32301 24210