Классификация, регрессия и другие алгоритмы Data Mining с использованием R

2.3 Модели для предсказания класса объектов

Классификация – наиболее часто встречающаяся задача машинного обучения, и заключается в построении моделей, выполняющих отнесение интересующего нас объекта к одному из нескольких известных классов. Существуют сотни методов классификации (см. Fernandez-Delgado et al., 2014), которые можно использовать для предсказания значения отклика с двумя и более классами. Возникает вопрос: отвечает ли такое множество потребностям реально решаемых задач?

Попробуем выделить основные характерные черты, отличающие эти методы. Во-первых, многое зависит от того, что является поставленной целью исследования: объяснение внутренних механизмов изучаемых процессов или только прогнозирование отклика. Если ставится задача “вскрытия” структуры взаимосвязей между независимыми переменными и откликом, то создаваемая модель должна в явном виде отображать их в виде наглядной схемы, либо осуществлять сравнительную оценку силы влияния отдельных переменных. Примерами хорошо интерпретируемых моделей классификации являются деревья решений, логистическая регрессия и модели дискриминации.

Если же основной задачей является достижение высокой общей точности предсказаний (overall accuracy) значения целевого признака \(y\) для объекта \(a\), то представление модели в явном виде не требуется. Изучаемый процесс, который часто имеет объективно сложный характер, представляется в виде “черного ящика”, а решающие процедуры могут иметь большое (до десятков тысяч) или неопределенное число трудно интерпретируемых параметров. Эффективными методами прогнозирования классов являются случайные леса, бустинг, бэггинг, искусственные нейронные сети, машины опорных векторов, групповой учет аргументов МГУА и др.

Во-вторых, некоторую систематичность в типизацию моделей классификации может внести их связь с тремя основными парадигмами машинного обучения: геометрической, вероятностной и логической. Обычно множество объектов имеет некую геометрическую структуру: каждый из них, описанный числовыми признаками, можно рассматриваться как точка в многомерной системе координат. Геометрическая модель разделения на классы строится в пространстве признаков с применением таких геометрических понятий, как прямые, плоскости и криволинейные поверхности (в общем виде “гиперплоскости”). Примеры моделей, реализующих геометрическую парадигму: логистическая регрессия, метод опорных векторов и дискриминантный анализ. Другим важным геометрическим понятием является функция расстояния между объектами, которая приводит к классификатору по ближайшим соседям.

Вероятностный подход заключается в предположении о существовании некоего случайного процесса, который порождает значения целевых переменных, подчиняющиеся вполне определенному, но неизвестному нам распределению вероятностей. Примером модели вероятностного характера является байесовский классификатор, формирующий решающее правило по принципу апостериорного максимума. Модели логического типа по своей природе наиболее алгоритмичны, поскольку легко выражаются на языке правил, понятных человеку, таких как: if <условие> = 1 then Y = <категория класса>. Примером таких моделей являются ассоциативные правила и деревья классификации. Некоторые авторы (Mount, Zumel, 2014, р. 91) подчеркивают различие терминов “предсказание” (prediction) и “прогнозирование” (forecasting). Предсказание лишь озвучивает результат (например, «Завтра будет дождь»), а при прогнозировании итог связывается с вероятностью события («Завтра с шансом 80% будет дождь»). Мы считаем, что на практике трудно провести между этими терминами четкую границу. К тому же, часто эта разница в совершенно не принципиальна – главное понимать контекст задачи.

Наконец, третьим основанием для группировки методов является природа наблюдаемых признаков, которые можно разделить на четыре типа: бинарные (0/1), категориальные, счетные и метрические. Имеются определенные нюансы при использовании перечисленных типов признаков в качестве предикторов, которые оговариваются нами ниже в рекомендациях по применению каждого метода моделирования. Например, бинарное пространство переменных некорректно использовать для линейного дискриминантного анализа. Однако принципиально важное значение имеет, к какому типу признаков относится отклик: задача классификации предполагает, что он измерен в бинарных, категориальных или, отчасти, порядковых шкалах.

Бинарный классификатор формирует некоторое диагностическое правило и оценивает, к какому из двух возможных классов следует отнести изучаемый объект (согласно медицинской терминологии условно назовем эти классы “норма” или “патология”). Группы точек “патология/норма” в заданном пространстве предикторов, как правило, статистически неразделимы: например, повышение температуры тела до 37.5C часто свидетельствует о заболевании, хотя не всегда болезнь может сопровождаться высокой температурой. Поэтому при тестировании модели вероятны ошибочные ситуации, такие как пропуск положительного (патологического) заключения FN или его “гипердиагностика” FP, т.е. отнесение нормального состояния к патологическому.

Результаты теста на некоторой контрольной выборке можно представить обычной таблицей сопряженности, которую часто называют матрицей неточностей (confusion matrix):

	Результаты теста:
Истинное состояние тест-объектов:	Предсказана патология (1)	Предсказана норма (0)
Патология (1)	Истинно-положительные `TP` (True positives)	Ложно-отрицательные `FN` (False negatives)
Норма (1)	Ложно-положительные `FP` (False positives)	Истинно-отрицательные `TN` (True negatives)

В этих обозначениях объективная ценность рассматриваемого бинарного классификатора определяется следующими показателями:

Чувствительность (sensitivity) \(SE = Err_{II} = TP / (TP + FN)\), определяющая насколько хорош тест для выявления патологических экземпляров;
Специфичность (specificity) \(SP = Err_{I} = FP / (FP + TN)\), показывающая эффективность теста для правильной диагностики отклонений от нормального состояния;
Точность (accuracy) \(AC = (TP + TN) / (TP + FP + FN + TN)\), определяющая общую вероятность теста давать правильные результаты.

По аналогии с классической проверкой статистических гипотез специфичность \(Err_I\) определяет ошибку I рода и, соответственно, вероятность нулевой гипотезы, тогда как чувствительность \(Err_{II}\) - мощность теста. Точность является, безусловно, наиболее широко известной мерой производительности классификатора, которая становится катастрофически некорректной в случае несбалансированных частот классов. Если, например, число пациентов, заболевших лихорадкой, составляет менее 1% от числа обследованных, то полный пропуск патологии даст вполне приличный результат тестирования 99%.

Рассмотрим популярный пример выделения спама (“spam” от слияния двух слов - “spiced” и “ham”, или “пряная ветчина”, как образец некачественного пищевого продукта) в электронных письмах в зависимости от встречаемости тех или иных слов (всего 58 частотных показателей). Выборка по спаму представлена в обширной коллекции наборов данных Центра машинного обучения и интеллектуальных систем Калифорнийского университета (UCI Machine Learning Repository) и после некоторой предварительной обработки используется для иллюстрации в книге Mount, Zumel (2014). Скачаем этот файл с сайта ее авторов и разделим исходные данные в соотношении 10:1 на обучающую и проверочную выборки:

spamD <- read.table('https://raw.github.com/WinVector/zmPDSwR/master/Spambase/spamD.tsv', 
                    header = TRUE, sep = '\t')
dim(spamD)

## [1] 4601   59

spamTrain <- subset(spamD, spamD$rgroup >= 10)
spamTest <- subset(spamD, spamD$rgroup < 10)
c(nrow(spamTrain), nrow(spamTest))

## [1] 4143  458

# Составляем список переменных и объект типа "формула"
spamVars <- setdiff(colnames(spamD), list('rgroup', 'spam'))
spamFormula <- as.formula(paste('spam=="spam"', 
                                paste(spamVars, collapse = ' + '), sep = ' ~ '))
spamModel <- glm(spamFormula, family = binomial(link = 'logit'), data = spamTrain)

# Добавляем столбец со значениями вероятности спама:
spamTrain$pred <- predict(spamModel, newdata = spamTrain, type = 'response')
spamTest$pred  <- predict(spamModel,newdata = spamTest, type = 'response')

Компоненты матрицы неточностей и перечисленные показатели легко получить с использованием обычной функции table() - например, так:

#  На обучающей выборке:
(cM.train <- table(Факт = spamTrain$spam, Прогноз = spamTrain$pred > 0.5))

##           Прогноз
## Факт       FALSE TRUE
##   non-spam  2396  114
##   spam       178 1455

#  На проверочной выборке:
(cM <- table(Факт = spamTest$spam, Прогноз = spamTest$pred > 0.5))

##           Прогноз
## Факт       FALSE TRUE
##   non-spam   264   14
##   spam        22  158

c(Точность <- (cM[1, 1] + cM[2, 2])/sum(cM), 
          Чувствительность <- cM[1, 1]/(cM[1, 1] + cM[2, 1]),
          Специфичность <- cM[2, 2]/(cM[2, 2] + cM[1, 2]))

## [1] 0.9213974 0.9230769 0.9186047

Иногда предпочтительнее использовать функцию confusionMatrix(y, pred) из пакета caret:

library(caret)
library(e1071)
pred <- ifelse(spamTest$pred > 0.5, "spam", "non-spam") 
confusionMatrix(spamTest$spam, pred)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction non-spam spam
##   non-spam      264   14
##   spam           22  158
##                                           
##                Accuracy : 0.9214          
##                  95% CI : (0.8928, 0.9443)
##     No Information Rate : 0.6245          
##     P-Value [Acc > NIR] : <2e-16          
##                                           
##                   Kappa : 0.834           
##  Mcnemar's Test P-Value : 0.2433          
##                                           
##             Sensitivity : 0.9231          
##             Specificity : 0.9186          
##          Pos Pred Value : 0.9496          
##          Neg Pred Value : 0.8778          
##              Prevalence : 0.6245          
##          Detection Rate : 0.5764          
##    Detection Prevalence : 0.6070          
##       Balanced Accuracy : 0.9208          
##                                           
##        'Positive' Class : non-spam        
##

Выбрать другой класс в качестве положительного исхода можно, задав аргумент positive = "spam". Функция предоставляет пользователю такие статистики, как доверительные интервалы и р-значение для точности, результаты теста \(\chi^2\) по Мак-Немару, вероятностный индекс \(\kappa\) (каппа) Дж. Коэна, а также еще шесть других критериев оценки эффективности классификатора, интересных, по всей вероятности, ограниченному кругу специалистов:

прогностическая ценность (prevalence) PV = (TP + FN)/(TP + FP + FN + TN);
положительная прогностическая ценность (вероятность фактической патологии при положительном диагнозе) PPV = SE*PV/(SE*PV + (1- SP)*(1 - PV));
отрицательная прогностическая ценность (вероятность отсутствия патологии при негативном результате теста) NPV = SP*(1 - PV)/(PV*(1 - SE) + SP*(1 - PV));
частота выявления (detection rate) DR = TP/( TP + FP + FN + TN);
частота распространения (detection drevalence) DP = (TP + FP)/(TP + FP + FN + TN); сбалансированная точность (balanced accuracy) BAC = (SE + SP)^2.

Эффективность классификатора может также оцениваться с использованием информационных критериев - энтропии \(E = \sum -p_i\log_2 p_i\), где \(p_i\) - вероятности каждого возможного исхода, и условной энтропии (conditional entropy). Эти меры могут быть рассчитаны с использованием функций:

entropy <- function(x) { 
    xpos <- x[x > 0]
    scaled <- xpos/sum(xpos) ; sum(-scaled*log(scaled, 2))
   }
print(entropy(table(spamTest$spam)))

## [1] 0.9667165

conditionalEntropy <- function(t) {
    (sum(t[, 1])*entropy(t[, 1]) + sum(t[, 2])*entropy(t[, 2]))/sum(t)
    }
print(conditionalEntropy(cM))

## [1] 0.3971897

Исходная энтропия Е = entropy(table(y)) определяет среднее количество информации, измеряемой в битах, которую мы приобретаем, если извлечь из выборки очередной экземпляр того или иного класса. Условная энтропия conditionalEntropy(table(y, pred)) показывает, насколько эта мера информации уменьшается из-за ошибок предсказания для различных категорий.

Общепринятым графоаналитическим методом оценки качества теста и интерпретации перечисленных показателей является ROC-анализ (от “Receiver Operator Characteristic” - функциональная характеристика приемника), название которого взято из методологии оценки качества сигнала при радиолокации.

ROC-кривая получается следующим образом (Goddard, Hinberg, 1989). Пусть мы имеем выборку значений независимого количественного показателя, который варьирует от xmin до xmax, и сопряженного с ним бинарного отклика (1 – патология, 0 – норма). Любое произвольное значение \(х\) на этом диапазоне может считаться классификационным порогом, или точкой отсечения (cutt-off value), делящим вектор \(y\) на два подмножества, и для этого разбиения можно рассчитать значения чувствительности \(SE\) и специфичности \(SP\). Если выполнить сканирование всех возможных значений \(x_{\max} \geq x \geq x_{\min}\), то можно построить график зависимости, где по оси Y откладывается \(SE\), а по оси X - \((1 - SP)\). Реализация этой процедуры в R может привести к ступенчатой или сглаженной кривой следующего вида (рис. 2.8):

# ROC кривая:
library(pROC)
m_ROC.roc <- roc(spamTest$spam, spamTest$pred)
plot(m_ROC.roc, grid.col = c("green", "red"), grid = c(0.1, 0.2),
     print.auc = TRUE, print.thres = TRUE)
plot(smooth(m_ROC.roc), col = "blue", add = TRUE, print.auc = FALSE)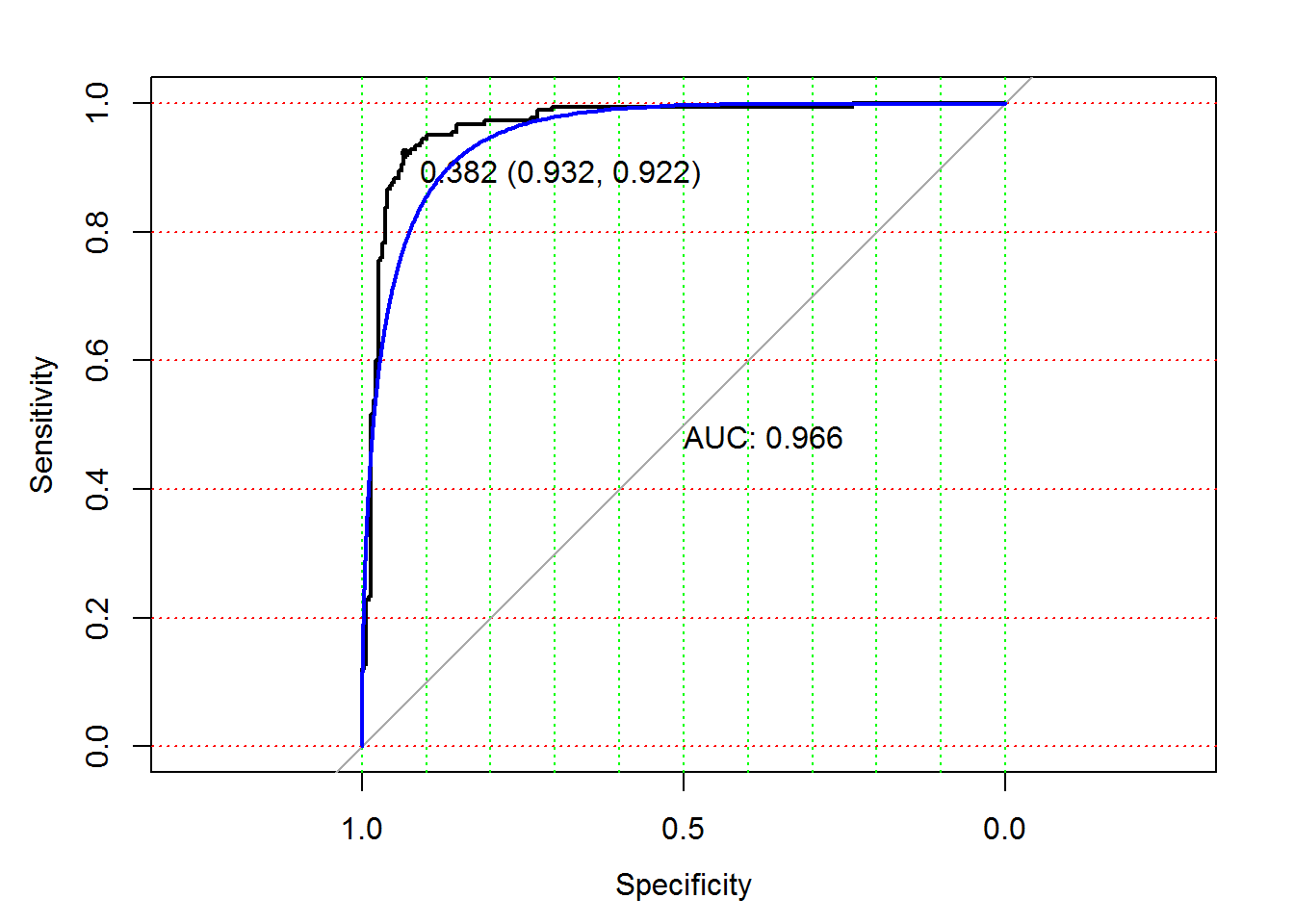

Рисунок 2.8: ROC-кривая для оценки вероятности спама

В случае идеального классификатора ROC-кривая проходит вблизи верхнего левого угла, где доля истинно-положительных случаев равна 1, а доля ложно-положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, главная диагональная линия соответствует “бесполезному” классификатору, который “угадывает” классовую принадлежность случайным образом. Следовательно, близость ROC-кривой к диагонали говорит о низкой эффективности построенной модели.

Для нахождения оптимального порога, соответствующего наиболее безошибочному классификатору, через крайнюю точку ROC-кривой проводят линию максимальной точности, параллельную главной диагонали. На приведенном графике такая точка, соответствующая значению х = 0.382, имеет наилучшую комбинацию значений чувствительности SE = 0.932 и специфичности SP = 0.922. Обратите внимание, что в качестве значений \(х\) фигурирует оценка вероятности отнесения к спаму и, видимо, мы совершенно напрасно принимали ранее в качестве порога величину 0.5.

Полезным показателем является численная оценка площади под ROC-кривыми AUC (Area Under Curve). Практически она изменяется от 0.5 (“бесполезный” классификатор) до 1.0 (“идеальная” модель). Показатель AUC предназначен исключительно для сравнительного анализа нескольких моделей, поэтому связывать его величину с прогностической силой можно только с большими допущениями.

В нашем примере в качестве классификатора писем со спамом мы использовали модель логистической регрессии, полагая, что бинарный отклик имеет биномиальное распределение. Напомним, что в случае обобщенных линейных моделей GLM вместо минимизации суммы квадратов отклонений ищется экстремум логарифма функции максимального правдоподобия (log maximum likelihood), вид которой зависит от характера распределения данных. В нашем случае логарифм функции правдоподобия LL численно равен сумме логарифмов вероятностей классов, которые модель правильно предсказывает для каждого наблюдения:

(LL <- logLik(spamModel))

## 'log Lik.' -807.0323 (df=58)

Как и в случае гауссова распределения (см. раздел 2.1), оценка адекватности биномиальной модели осуществляется с использованием девианса D = -2(LL - S), где S = 0 - правдоподобие “насыщенной модели” с минимальным уровнем байесовской ошибки. Исходя из априорной вероятности одного из классов, можно рассчитать логарифм правдоподобия и девианс для нулевой модели D.null. Эффективность классификатора определяется соотношением девианса остатков D и нуль-девианса D.null, что соответствует псевдо-коэффициенту детерминации Rsquared модели. Статистическую значимость разности девиансов (D.null - D) можно оценить по критерию \(\chi^2\):

df <- with(spamModel, df.null - df.residual)
c(D.null <- spamModel$null.deviance,
  D <- spamModel$deviance,
  Rsquared = 1 - D/D.null,
  pchisq(D.null - D, df, lower.tail = FALSE))

##                               Rsquared              
## 5556.3602041 1614.0646078    0.7095104    0.0000000

Мы получили модель, вполне адекватную по отношению к имеющимся данным. Разумеется, все эти вычисления могут быть выполнены с использованием базовых функций summary() и anova():

summary(spamModel)

Null_Model <- glm(spam ~ 1, family = binomial(link = 'logit'), data = spamTrain)

anova(spamModel, Null_Model , test = "Chisq")

Мы не станем приводить здесь длинные протоколы с результатами этих процедур, включающие статистический анализ 58 коэффициентов модели. Отложим также для специального раздела обсуждение возможных путей решения проблемы поиска оптимального состава предикторов.

Вероятностные модели логита, как и иные детерминированные классификаторы, выполняют предсказание класса каждого тестируемого объекта, но при этом возвращают также оцененную вероятность такой принадлежности. При этом весьма полезно проанализировать график плотности распределения вероятностей обоих классов, особенно при подборе оптимальных пороговых значений классификатора. Следующая команда R обеспечивает построение такого графика:

ggplot(data = spamTest) + 
    geom_density(aes(x = pred, color = spam, linetype = spam))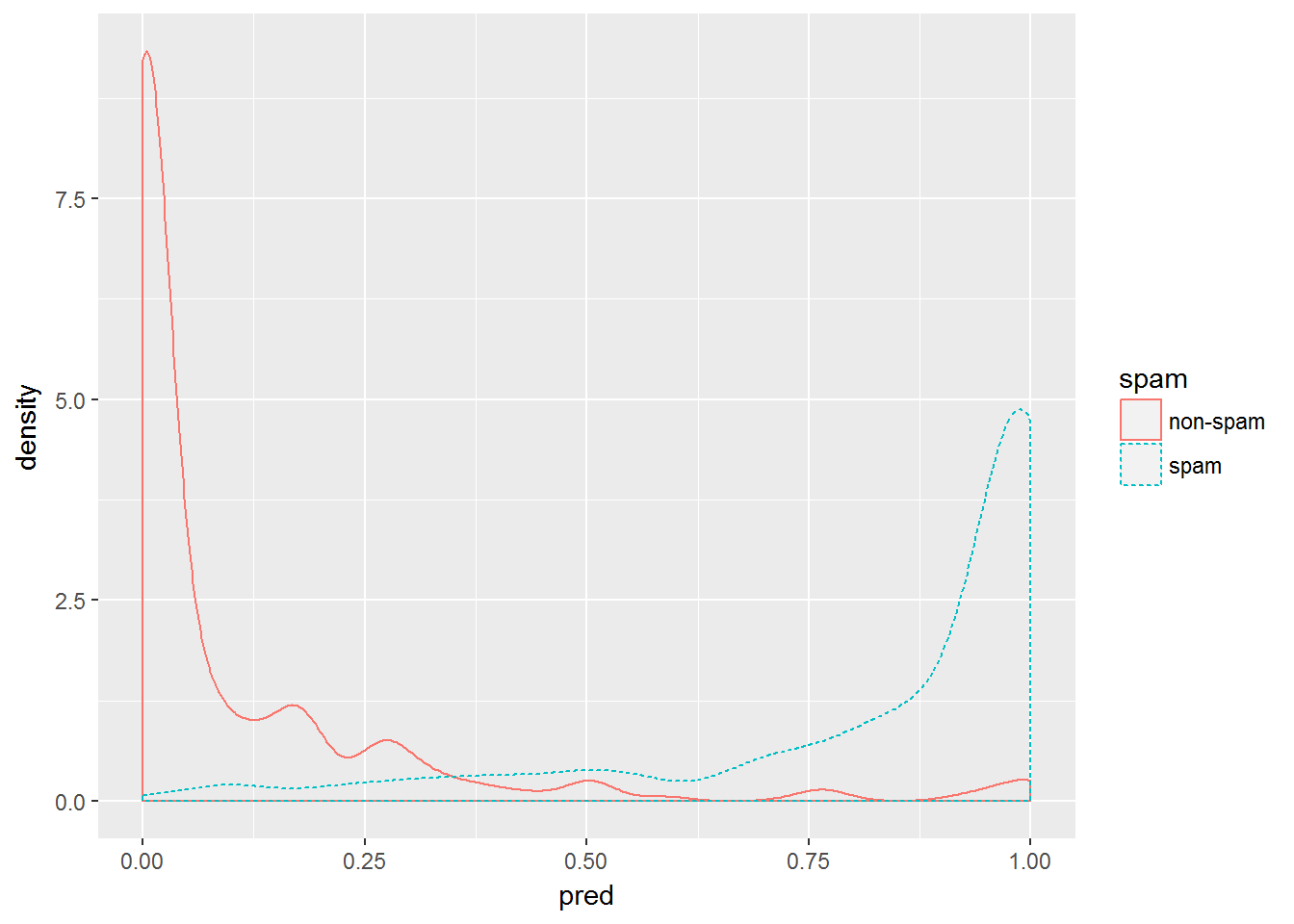

Кривые плотности апостериорной вероятности принадлежности объектов к двум классам: электронным письмам с наличием спама и без него

Рисунок 2.9: Кривые плотности апостериорной вероятности принадлежности объектов к двум классам: электронным письмам с наличием спама и без него