4.6 Деревья регрессии с многомерным откликом

В разделе 4.3 мы рассмотрели деревья CART, прогнозирующие конкретное значение одной зависимой переменной Y. Развитием этих идей являются деревья многомерной классификации и регрессии (MRT, Multivariate Regression Trees - De’Ath, 2002). Если в случае обычной регрессии строится модель, прогнозирующая значения одномерного вектора, то многомерный отклик задается в виде двумерной таблицы, содержащей несколько столбцов наблюдаемых признаков. Ставится задача оценить, какие предикторы и в какой степени влияют на совокупную изменчивость количественных соотношений между отдельными компонентами отклика.

Как и в одномерном случае, деревья MRT формируются в результате рекурсивной процедуры разделения строк таблицы данных на гомогенные подмножества, которая реализуется с использованием набора внешних количественных или категориальных независимых переменных \(\mathbf{X}\). “Листьями” полученного дерева являются кластеры объектов, скомпонованные таким образом, чтобы минимизировать различия между точками в многомерном пространстве в пределах каждой совокупности.

Искомым критерием, минимизирующим внутригрупповые различия, может быть, например, сумма квадратов отклонений \(SS_D = \sum_{ij} (y_{ij} - \bar{y}_j)^2\), где где \(y_{ij}\) - значение показателя отклика \(j\) для наблюдения \(i\); \(\bar{y}_j\) средние значения этого показателя для формируемого кластера, куда включается \(i\)-е наблюдение. Геометрически \(SS_D\) можно представить как сумму евклидовых расстояний от объединяемых объектов до центра их группировки.

Процедура многомерной классификации состоит из последовательности шагов, на каждом из которых синхронно выполняются следующие действия: (а) бинарное разбиение объектов на группы, обусловленное значением одной из независимых переменных, и (б) перекрестная проверка полученных результатов.

Рассмотрим построение дерева MRT на знакомом нам по предыдущим разделам примере анализа обилия водорослей в зависимости от гидрохимических показателей воды и условий отбора проб в водотоках. Для переменных a1-a7, описывающих численности 7 групп водорослей, выполним преобразование Бокса-Кокса и шкалирование, что даст нам возможность соизмерить между собой значения различных показателей и корректно вычислить статистики \(SS_D\):

load(file = "algae.RData") # Загрузка таблицы algae - раздел 4.1

library(caret)
Transal <- preProcess(algae[, 12:18], method = c("BoxCox", "scale"))
Species <- predict(Transal, algae[, 12:18])

Построение дерева MRT будем осуществлять с использованием функции mvpart() из пакета mvpart. В левой части формулы, задающей структуру модели, представим матрицу из трансформированных численностей семи групп водорослей Species, а в правой части - независимые гидрохимические показатели рек algae[, 1:11]:⁸

library(mvpart) 
spe.mvpart <- mvpart(data.matrix(Species) ~ ., algae[, 1:11], 
                     xv = "pick", xval = nrow(Species),
                     xvmult = 1, margin = 0.08, which = 4, bars = TRUE)

Здесь параметры xval и xvmult соответствуют числу блоков и повторностей перекрестной проверки, т.е. при xval = nrow(Species) осуществляется скользящий контроль. Аргументы margin (ширина полей), which (расположение текста) и bars (вывод столбиковых диаграмм) задают атрибуты визуализации дерева. Важный параметр xv определяет условие выбора числа листьев дерева: при значении "best" оно определяется автоматически по результатам перекрестной проверки, а при "pick" размеры дерева можно выбрать интерактивно, выполнив щелчок мышью по следующему графику (рис. 4.20):

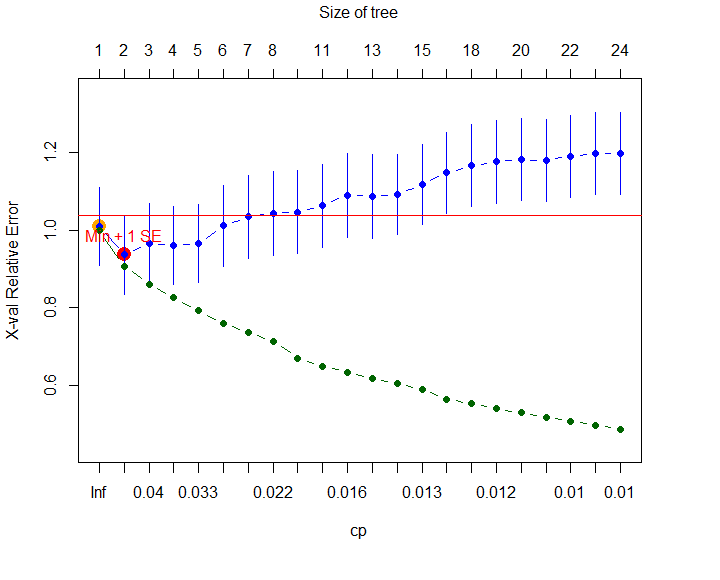
Рисунок 4.20: Зависимость относительной ошибки перекрестной проверки от числа узлов дерева

Из представленного графика видно, что при увеличении размеров дерева ошибка на обучающей выборке (зеленые точки) постоянно уменьшается, а ошибка перекрестной проверки - монотонно возрастает (синие точки). Рекомендуемое число листьев в точке их пересечения - 2. Однако, если в предыдущих сообщениях нам было важно получить максимальную точность моделей при прогнозировании, то в случае моделей МRТ более важна их объясняющая составляющая. Поэтому, чтобы выполнить содержательный анализ зависимости свойств найденных групп водорослей от внешних факторов, разделим все множество наблюдений на 4 кластера и изобразим полученное дерево графически (рис. 4.21):

plot(spe.mvpart)
text(spe.mvpart)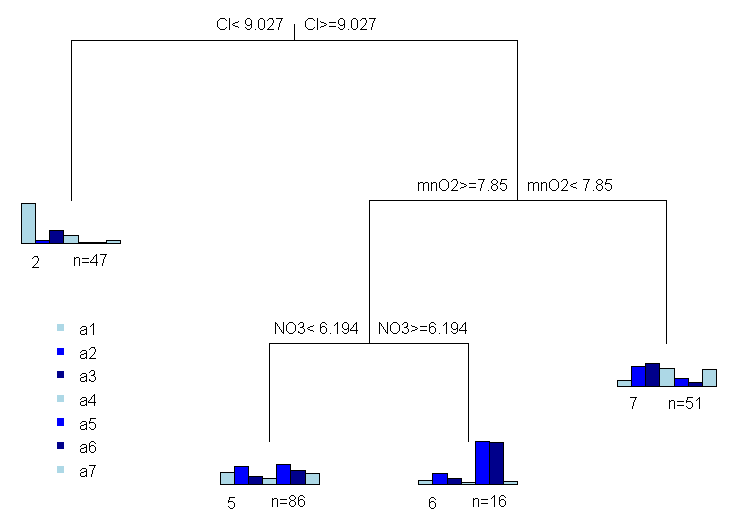  

Рисунок 4.21: Построенное дерево с многомерным откликом

Рассмотрим более внимательно некоторые нюансы итеративной процедуры построения модели MRT:

summary(spe.mvpart) # Протокол приведен с сокращениями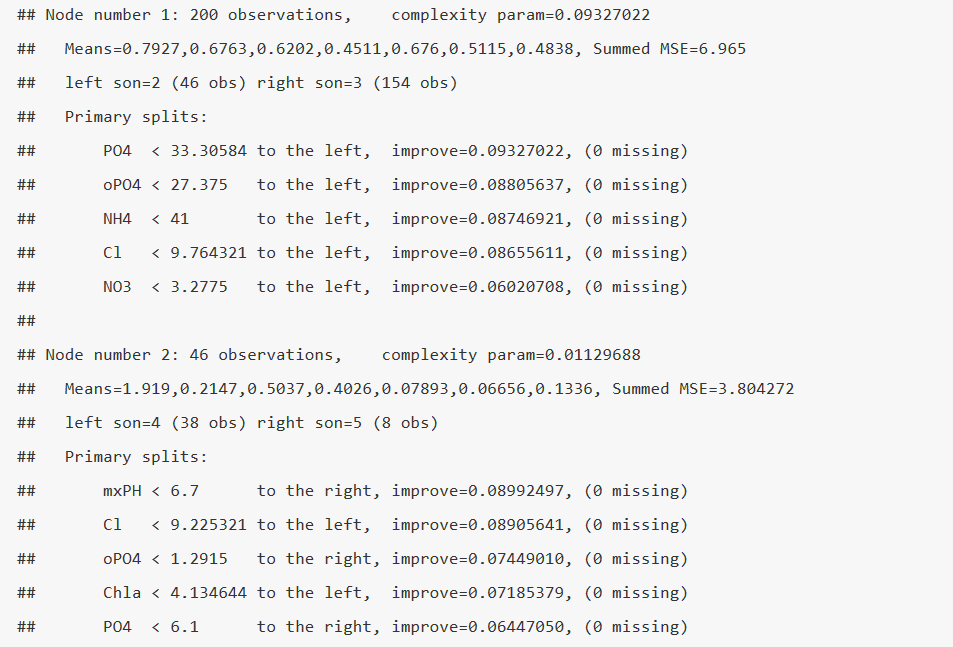

На первом шаге Node number 1 рассматриваются все варианты разбиения исходной выборки на две части при разных опорных значениях независимых факторов и выбирается такой из них (в нашем случае хлориды Cl < 9.0275), который в наибольшей мере обеспечивает статистическую гомогенность формируемых кластеров (complexity param = 0.0956423). Кластер 2 из 47 наблюдений на последующих шагах не разбивается, а 153 наблюдения слева вновь делятся на два подмножества по условию mnO2 < 7.85 в соотношении 51 + 102. Последнее подмножество по условию NO3 < 6.194 в свою очередь делится на два кластера, на чем итерации завершаются.

Анализ многомерного отклика сообщества водорослей с помощью деревьев MRT предоставляет исследователю много дополнительных возможностей интерпретации результатов. В первую очередь, это связано с оценкой того, какие компоненты отклика и их ассоциации инициируют разбиение исходной совокупности на узлах дерева и предопределяют состав сформированных подмножеств объектов:

# Относительная доля групп водорослей в кластерах
groups.mrt <- levels(as.factor(spe.mvpart$where))
leaf.sum <- matrix(0, length(groups.mrt), ncol(Species))  
colnames(leaf.sum) <- colnames(Species)
rownames(leaf.sum) <- groups.mrt
for (i in 1:length(groups.mrt)){
    leaf.sum[i,] <- apply(Species[which
                                  (spe.mvpart$where == groups.mrt[i]), ], 2, sum)
} 

head(round(leaf.sum, 3))

##        a1     a2     a3     a4     a5     a6    a7
## 4  68.759  9.458 16.205  5.093  3.631  2.624 5.816
## 5   3.082  0.000  6.404  0.815  0.000  0.000 0.000
## 6  16.437  0.417  0.561 12.609  0.000  0.437 0.330
## 12 11.931 18.843  4.591  5.592 22.853 10.094 5.719
## 14 18.254  5.296  8.980  3.871  8.183  5.334 2.210
## 15 10.521  0.091  0.245  0.226  0.387  0.120 0.194

Разумеется, эти суммы не соответствуют значениям абсолютных численностей водорослей, поскольку набор исходных данных подвергался преобразованию Бокса-Кокса и шкалированию.

#  Вывод диаграммы типа "разрезанный пирог"
par(mfrow = c(2, 2)) ; for (i in 1:length(groups.mrt)){
    pie(leaf.sum[i, which(leaf.sum[i,] > 0)], radius = 1, 
        main = paste("Кл. №", groups.mrt[i])) }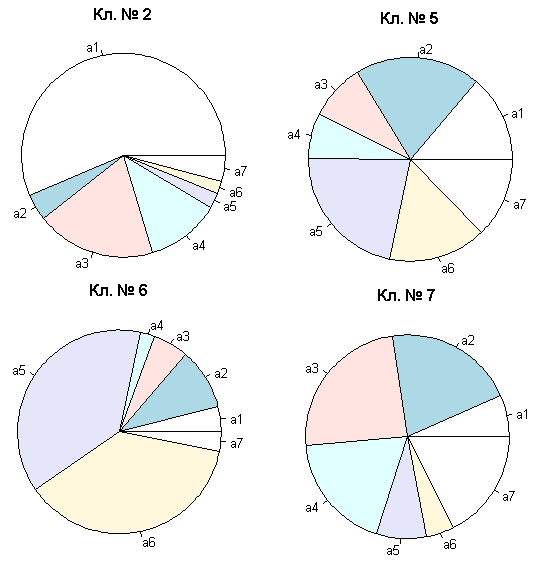

Рисунок 4.22: Диаграммы долей средних численностей групп водорослей

Мы получили диаграммы долей усредненных численностей групп водорослей для четырех кластеров, составивших “листья” МRТ (рис. 4.22). Их визуальный анализ показывает, что подмножество 2 составлено с явным доминированием группы a1, подмножество 6 - с доминированием групп a5 и a6, а два остальных кластера не имеют столь характерных признаков. Видимо, перекрестная проверка все же имела все основания рекомендовать нам разбиение только на два кластера.

Можно также оценить, насколько велика неоднородность между кластерами, выполнив редукцию многомерного отклика Species и проецирование данных из многомерного пространства на плоскость с осями из двух первых главных компонент (СА). На сформированной диаграмме конкретные наблюдения, отнесенные МRТ к разным кластерам, выделены отдельные цветами и обозначены контуром, проведенным через крайние точки. В центрах тяжести областей каждого из четырех блоков данных помещен крупный кружок, обозначающий их центроид.

#  Вывод диаграммы РСА
rpart.pca(spe.mvpart)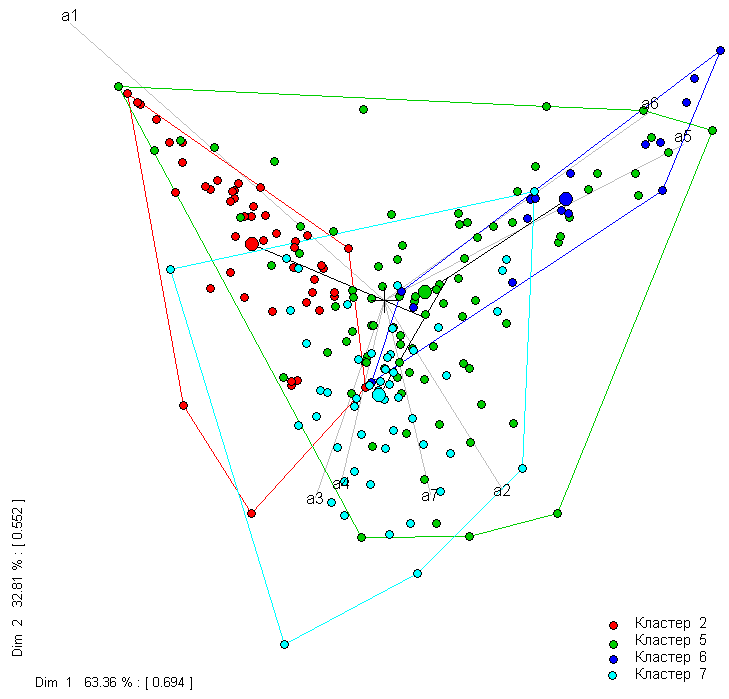

Рисунок 4.23: Диаграмма четырех групп водорослей в пространстве двух главных компонент

Из центра координат диаграммы проводятся дополнительные оси ординации, косинусы углов между которыми соответствуют коэффициентам корреляции между каждой парой из 7 групп водорослей. Проекции точек на каждую ось ординации определяют характер распределения показателя по кластерам с разными внешними факторами. Например, на ось а1 проецируются в основном красные точки кластера 2, объединяющего наблюдения с низким содержанием хлоридов Cl < 9.0275.

Настоящий раздел можно рассматривать в качестве “реквиема” по этому весьма оригинальному и практически полезному пакету: mvpart был удален из репозитория CRAN и для версий R выше 3.1 отсутствует. Это уже не первый случай, когда авторы перестают поддерживать важные и популярные функциональные компоненты: например, та же участь постигла удачный пакет lmRepm, в котором функции построения линейных моделей lm() и anova() при оценке статистических критериев используют перестановочные алгоритмы и не столь жестко связаны с предположениями о характере распределения данных.

Выхода из подобной ситуации может быть два. Во-первых, ничто не мешает установить на компьютер несколько версий R (так, один авторов этой книги при любой возможности отдает предпочтение старенькой, но симпатичной версии 2.12). Другая возможность - осуществить компиляцию последней версии пакета mvpart_1.6-2 из архива CRAN в вашей текущей версии R (см. рекомендации в сообщении на http://stackoverflow.com).