ГЛАВА 6 Бинарные классификаторы с различными разделяющими поверхностями
6.1 Дискриминантный анализ
Линейный дискриминантный анализ (Linear Discriminant Analysis, LDA) является разделом многомерного анализа, который позволяет оценивать различия между двумя и более группами объектов по нескольким переменным одновременно (Афифи, Эйзенс, 1982; Айвазян и др., 1989). Он реализует две тесно связанные между собой статистические процедуры:
- интерпретацию межгрупповых различий, когда нужно ответить на вопрос: насколько хорошо используемый набор переменных в состоянии сформировать разделяющую поверхность для объектов обучающей выборки и какие из этих переменных наиболее информативны?
- классификацию, т.е предсказание значения группировочного фактора для экзаменуемой группы наблюдений.
В основе дискриминантного анализа лежит предположение о том, что описания объектов каждого \(k\)-го класса представляют собой реализации многомерной случайной величины, распределенной по нормальному закону \(N_m(\mu_k; \Sigma_k)\) со средними \(\mu_k\) и ковариационной матрицей \[\mathbf{C}_k = \frac{1}{n_k - 1} \sum_{i=1}^{n_k} (\mathbf{x}_{ik} - \mathbf{\mu}_k)^T (\mathbf{x}_{ik} - \mathbf{\mu}_k)\]
(индекс \(m\) указывает на размерность признакового пространства).
Рассмотрим несколько упрощенную геометрическую интерпретацию алгоритма LDA для случая двух классов. Пусть дискриминантные переменные \(\boldsymbol{x}\) - оси \(m\)-мерного евклидова пространства. Каждый объект (наблюдение) является точкой этого пространства с координатами, представляющими собой фиксируемые значения каждой переменной. Если оба класса отличаются друг от друга по наблюдаемым переменным, их можно представить как скопления точек в разных областях рассматриваемого пространства, которые могут частично перекрываться. Для определения положения каждого класса можно вычислить его “центроид”, который является воображаемой точкой, координатами которой являются средние значения переменных в данном классе.
Задача дискриминантного анализа заключается в проведении дополнительной оси \(z\), которая проходит через облако точек таким образом, что проекции на нее обеспечивают наилучшую разделяемость на два класса. Ее положение задается линейной дискриминантной функцией (linear discriminant, LD) с весовыми коэффициентами \(\beta_j\), определяющими вклад каждой исходной переменной \(x_j\): \[z(\boldsymbol{x}) = \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_m x_m.\]
Если сделать предположение, что ковариационные матрицы объектов классов 1 и 2 равны, т.е. \(\mathbf{C = C_1 = C_2}\), то вектор коэффициентов \({\beta_1, \dots, \beta_m}\) линейного дискриминанта \(z(\boldsymbol{x})\) может быть вычислен по формуле \(\boldsymbol{\beta} \mathbf{= C^{-1}(\mu_1 - \mu_2)}\), где \(\mathbf{C^{-1}}\) - матрица, обратная к ковариационной, \(\mathbf{\mu_k}\) вектор средних \(k\)-го класса. Полученная ось совпадает с уравнением прямой, проходящей через центроиды двух групп объектов классов, а обобщенное расстояние Махаланобиса, равное дистанции между ними в многомерном пространстве признаков, оценивается как \[D^2 = \mathbf{\beta (\mu_1 - \mu_2)}.\]
Таким образом, в LDA кроме предположения о нормальности распределения данных в каждом классе, которое на практике выполняется довольно редко, выдвигается еще и более серьезное предположение о статистическом равенстве внутригрупповых матриц дисперсий и корреляций. Если между ними нет серьезных отличий, их объединяют в расчетную ковариационную матрицу \[\mathbf{C = \left( C_1(n_1 - 1) + C_2(n_2 -1) \right) / (n_1 + n_2 -2)}.\]
По поводу искусственного объявления ковариационных матриц статистически неразличимыми существуют два различных мнения: одни исследователи считают, что могут оказаться отброшенными наиболее важные индивидуальные черты, характерные для каждого из классов и имеющие большое значение для хорошего разделения, тогда как другие - что это условие не является критическим для эффективного применения дискриминантного анализа. Тем не менее, проверка исходных предположений всегда остается правилом хорошего тона в статистике.
Для проверки гипотезы о многомерном нормальном распределении данных используется многомерная версия критерия согласия Шапиро-Уилка, которая реализована в функции mshapiro.test() из пакета mvnormtest. На вход этой функции подается матрица, строки которой соответствуют переменным, а столбцы - наблюдениям.
В разделах 2.4-2.5 мы подробно рассматривали пример анализа зависимости между двумя различными способами производства листового стекла (флэш-стекло и по принципу вертикального вытягивания) и составом его химических ингредиентов. С использованием статистики Пиллая и критерия Хотеллинга была показана статистическая значимость такой связи. Применим многомерный критерий Шапиро-Уилка к оценке характера распределения этой выборки:
DGlass <- read.table(file = "Glass.txt", sep = ",",
header = TRUE, row.names = 1)DGlass$FAC <- as.factor(ifelse(DGlass$Class == 2, 2, 1))
library(mvnormtest)
mshapiro.test(t(DGlass[DGlass$FAC == 1, 1:9])) ##
## Shapiro-Wilk normality test
##
## data: Z
## W = 0.19652, p-value < 2.2e-16mshapiro.test(t(DGlass[DGlass$FAC == 2, 1:9]))##
## Shapiro-Wilk normality test
##
## data: Z
## W = 0.13679, p-value < 2.2e-16Для обеих групп выявлены значимые отклонения от многомерного нормального распределения.
Для проверки гипотезы о гомогенности матриц ковариаций используется так называемый M-критерий Бокса, который реализован в функции boxM() из пакета biotools:
library(biotools) ## ---
## biotools version 3.0boxM(as.matrix(DGlass[, 1:9]), DGlass$FAC) ##
## Box's M-test for Homogeneity of Covariance Matrices
##
## data: as.matrix(DGlass[, 1:9])
## Chi-Sq (approx.) = 443.18, df = 45, p-value < 2.2e-16Гетерогенность матриц ковариаций также статистически значима.
Дискриминантный анализ реализован в нескольких пакетах для R, но мы рассмотрим применение функции lda() из базового пакета MASS. Поскольку важной характеристикой прогнозирующей эффективности модели является ее ошибка при перекрестной проверке, то в функции lda() пакета MASS заложена реализация скользящего контроля (leave-one-out CV). Напомним, что при этом из исходной выборки поочередно отбрасывается по одному объекту, строится \(n\) моделей дискриминации по (n – 1) выборочным значениям, а исключенное наблюдение каждый раз используется для учета ошибки классификации.
Составим предварительно функцию, которая по построенной модели выводит нам важные показатели для оценки ее качества: матрицы неточностей на обучающей выборке и при перекрестной проверке, ошибку распознавания и расстояние Махалонобиса между центроидами двух классов. С использованием этой функции оценим эффективность дискриминационной модели прогнозирования способа производства стекла по его химическому составу (см. разделы 2.4-2.5):
# Функция вывода результатов классификации
Out_CTab <- function(model, group, type = "lda") {
# Таблица неточностей "Факт/Прогноз" по обучающей выборке
classified <- predict(model)$class
t1 <- table(group, classified)
# Точность классификации и расстояние Махалонобиса
Err_S <- mean(group != classified)
mahDist <- NA
if (type == "lda")
{ mahDist <- dist(model$means %*% model$scaling) }
# Таблица "Факт/Прогноз" и ошибка при скользящем контроле
t2 <- table(group, update(model, CV = T)$class -> LDA.cv)
Err_CV <- mean(group != LDA.cv)
Err_S.MahD <- c(Err_S, mahDist)
Err_CV.N <- c(Err_CV, length(group))
cbind(t1, Err_S.MahD, t2, Err_CV.N)
}
# --- Выполнение расчетов
library(MASS)
lda.all <- lda(FAC ~ ., data = DGlass[, -10])
Out_CTab(lda.all, DGlass$FAC) ## 1 2 Err_S.MahD 1 2 Err_CV.N
## 1 69 18 0.2515337 66 21 0.3067485
## 2 23 53 1.2414682 29 47 163.0000000Отметим существенный рост ошибки распознавания до 31% при выполнении скользящего контроля. Естественно задаться вопросом, какие из имеющихся 9 признаков являются информативными при разделении, а какие - сопутствующим балластом. Шаговая процедура выбора переменных при классификации, реализованная функцией stepclass() из пакета klaR, основана на вычислении сразу четырех параметров качества моделей-претендентов: а) индекса ошибок (correctness rate), б) точности (accuracy), основанной на евклидовых расстояниях между векторами “факта” и “прогноза”, в) способности к разделимости (ability to seperate), также основанной на расстояниях, и г) доверительных интервалах центроидов классов. Все эти параметры оцениваются в режиме многократной перекрестной проверки.
library(klaR)
stepclass(FAC ~ ., data = DGlass[, -10], method = "lda")## correctness rate: 0.70515; in: "Al"; variables (1): Al
## correctness rate: 0.77978; in: "Ca"; variables (2): Al, Ca
##
## hr.elapsed min.elapsed sec.elapsed
## 0.00 0.00 0.72## method : lda
## final model : FAC ~ Al + Ca
## <environment: 0x000000001761a930>
##
## correctness rate = 0.7798lda.step <- lda(FAC ~ Mg + Al, data = DGlass[, -10])В результате получили компактную дискриминантную функцию \[z(x) = 2.69Al - 0.83Mg,\]
зависящую только от двух переменных. Найдем ошибку предсказания как на обучающей выборке, так и при скользящем контроле:
partimat(FAC ~ Mg + Al, data = DGlass[, -10], main = '', method = "lda")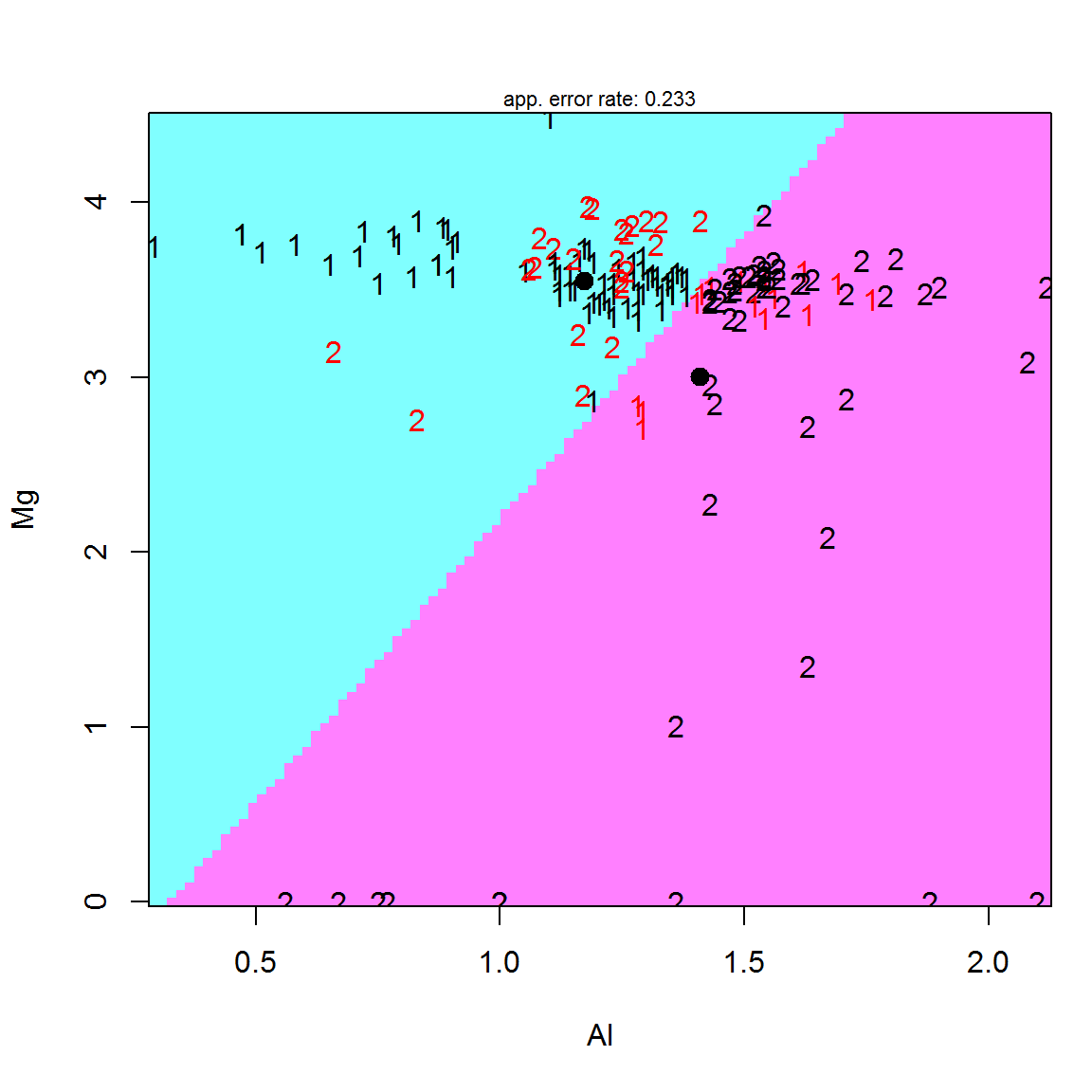
Рисунок 6.1: Диаграмма дискриминации двух классов 1 и 2 (ошибочное распознавание выделено шрифтом красного цвета); показаны линейная дискриминантная функция z и жирными точками - положение центроидов
Out_CTab(lda.step, DGlass$FAC)## 1 2 Err_S.MahD 1 2 Err_CV.N
## 1 72 15 0.2331288 72 15 0.2392638
## 2 23 53 1.0924355 24 52 163.0000000По обоим критериям ошибка предсказания сокращенной модели существенно ниже аналогичных показателей при использовании полного набора переменных. Это отражает общие методические закономерности, важные при выборе алгоритмов классификации и анализе результатов их работы:
- ошибка перекрестной проверки \(E_{CV}\) всегда превышает внутреннюю ошибку модели \(E_S\) на самой обучающей выборке и является объективной характеристикой качества распознавания на внешнем дополнении;
- сокращение размерности модели за счет выбора комплекса информативных переменных может увеличить ошибку \(E_S\), но, как правило, снижает ошибку скользящего контроля \(E_{CV}\).
Сокращение числа переменных до двух позволяет построить частный двумерный график, интерпретирующий процесс классификации (рис. 6.1).
Вместо функции stepclass() из пакета klaR для выбора оптимального набора предикторов можно воспользоваться функцией rfe() из пакета caret (процедура рекурсивного исключения - см. раздел 4.1):
ldaProfile <- rfe(DGlass[, 1:9], DGlass$FAC, sizes = 2:9,
rfeControl = rfeControl(functions = ldaFuncs,
method = "repeatedcv", repeats = 6))Для того чтобы уточнить, какую из трех построенных моделей следует предпочесть, выполним их тестирование на основе 10-кратной перекрестной проверки с 5 повторностями:
DGlass$FAC <- as.factor(ifelse(DGlass$Class == 2, "C2", "C1"))
# Модель на основе всех 9 предикторов
lda.full.pro <- train(DGlass[, 1:9], DGlass$FAC,
data = DGlass, method = "lda",
trControl = trainControl(method = "repeatedcv", repeats = 5,
classProbs = TRUE), metric = "Accuracy")
# Модель на основе 2 предикторов stepclass
lda.step.pro <- train(FAC ~ Mg + Al, data = DGlass, method = "lda",
trControl = trainControl(method = "repeatedcv", repeats = 5,
classProbs = TRUE), metric = "Accuracy")
# Модель на основе 3 предикторов rfe
lda.rfe.pro <- train(FAC ~ Al + K + Fe,
data = DGlass, method = "lda",
trControl = trainControl(method = "repeatedcv", repeats = 5,
classProbs = TRUE), metric = "Accuracy")
plot(varImp(lda.full.pro))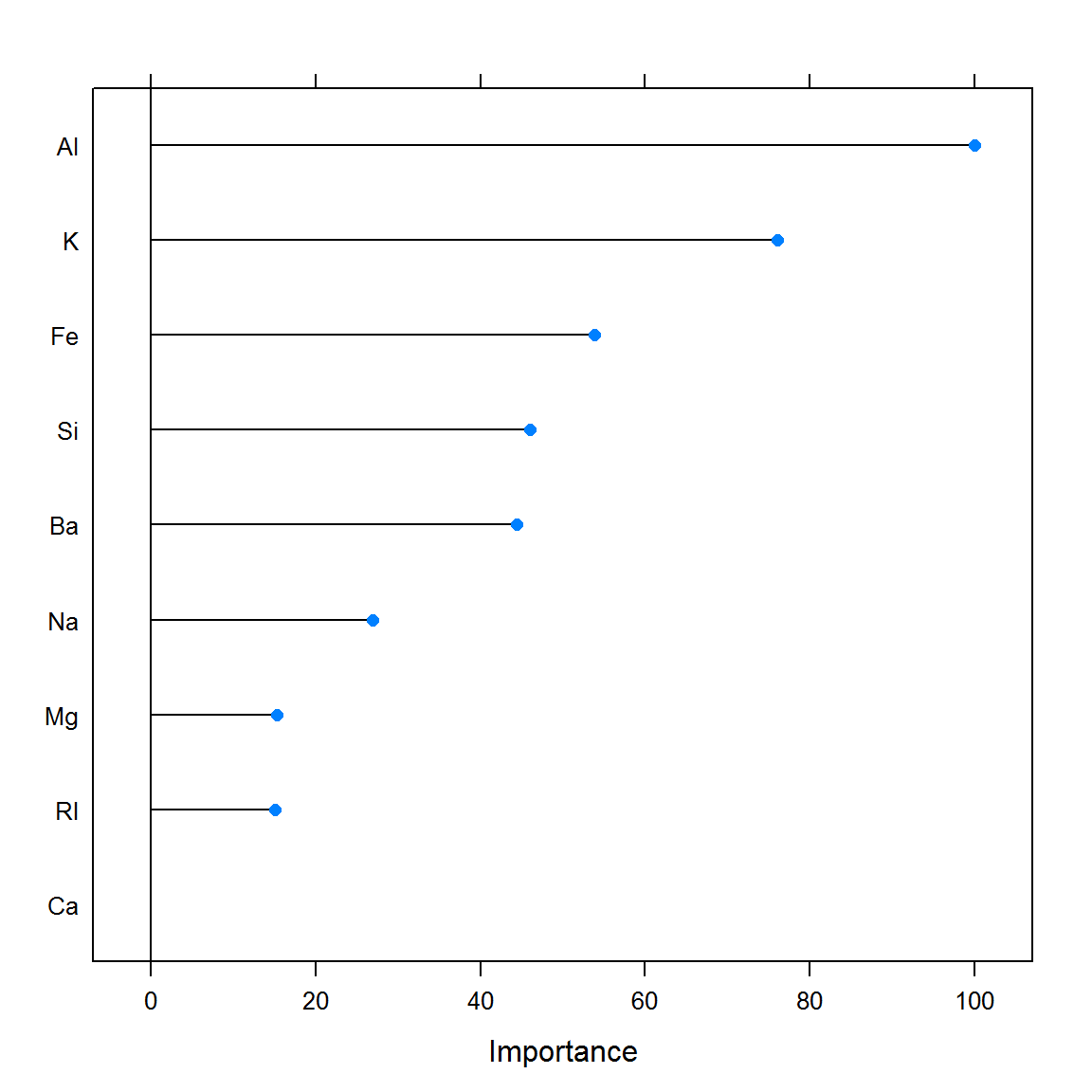
Рисунок 6.2: Значения важности отдельных переменных на основе абсолютных значений t-статистики при построении модели дискриминантного анализа
Функция rfe() провела отбор переменных в полном соответствии с рейтингом их важности на рис. 6.2, но это решение оказалось неоптимальным. Модель lda.step, полученная с использованием функции stepclass(), оказалась существенно эффективней.