5.4 Алгоритмы выделения ассоциативных правил
Ассоциативные правила представляют собой механизм нахождения логических закономерностей между связанными элементами (событиями или объектами). Пусть имеется \(\mathbf{A} = \{a_1, a_2, a_3, \dots, a_n\}\) - конечное множество уникальных элементов (list of items). Из этих компонентов может быть составлено множество наборов \(\mathbf{T}\) (sets of items), т.е. \(\mathbf{T} \subseteq \mathbf{A}\).
Ассоциативные правила \(\mathcal{A} \rightarrow \mathcal{T}\) имеют следующий вид: если <условие> то <результат>, где в отличие от деревьев классификации, <условие> - не логическое выражение, а набор объектов из множества \(\mathbf{A}\), с которыми связаны (ассоциированы) объекты того же множества, включенные в <результат> данного правила. Например, ассоциативное правило если (смородина, тля) то (муравьи) означает, что если на кусте смородины встретилась тля, то ищи поблизости и муравьев.
Понятие “вид элемента \(a_k\)” легко может быть обобщено на ту или иную его категорию или вещественное значение, т.е. концепция ассоциативного анализа может быть применена для комбинаций любых переменных. Например, при прогнозировании погоды одно из ассоциативных правил может выглядеть так: 'направление ветра' = NNW -> 'завтра будет дождь' = TRUE
Выделяют три вида правил:
- полезные правила, содержащие действительную информацию, которая ранее была неизвестна, но имеет логическое объяснение;
- тривиальные правила, содержащие действительную и легко объяснимую информацию, отражающую известные законы в исследуемой области, и поэтому не приносящие какой-либо пользы;
- непонятные правила, содержащие информацию, которая не может быть объяснена (такие правила или получают на основе аномальных исходных данных, или они содержат глубоко скрытые закономерности, и поэтому для интерпретации непонятных правил нужен дополнительный анализ).
Поиск ассоциативных правил обычно выполняют в два этапа:
- в пуле имеющихся признаков \(\mathbf{A}\) находят наиболее часто встречающиеся комбинации элементов \(\mathbf{T}\);
- из этих найденных наиболее часто встречающихся наборов формируют ассоциативные правила.
Для оценки полезности и продуктивности перебираемых правил используются различные частотные критерии, анализирующие встречаемость кандидата в массиве экспериментальных данных. Важнейшими из них являются поддержка (support) и достоверность (confidence). Правило \(\mathcal{A} \rightarrow \mathcal{T}\) имеет поддержку \(s\), если оно справедливо для \(s\%\) взятых в анализ случаев:
\[\text{support}(\mathcal{A} \rightarrow \mathcal{T}) = P(\mathcal{A} \cup \mathcal{T})\]
Достоверность правила показывает, какова вероятность того, что из наличия в рассматриваемом случае условной части правила следует наличие заключительной его части (т.е. из \(\mathcal{A}\) следует \(\mathcal{T}\)):
\[\text{confidence}(\mathcal{A} \rightarrow \mathcal{T}) = P(\mathcal{A} \cup \mathcal{T})/P(\mathcal{A}) = \text{support}(\mathcal{A} \rightarrow \mathcal{T})/\text{support}(\mathcal{A}).\]
Алгоритмы поиска ассоциативных правил отбирают тех кандидатов, у которых поддержка и достоверность выше некоторых наперед заданных порогов: minsupport и minconfidence. Если поддержка имеет большое значение, то алгоритмы будут находить правила, хорошо известные аналитику или настолько очевидные, что нет никакого смысла проводить такой анализ. Большинство интересных правил находят именно при низком значении порога поддержки. С другой стороны, низкое значение minsupport ведет к генерации огромного количества вариантов, что требует существенных вычислительных ресурсов или ведет к генерации статистически необоснованных правил.
В пакете arules для R используются и другие показатели - подъемная сила, или лифт (lift), которая показывает, насколько повышается вероятность нахождения \(\mathcal{T}\) в анализируемом случае, если в нем уже имеется \(\mathcal{A}\):
\[\text{lift}(\mathcal{A} \rightarrow \mathcal{T}) = \text{confidence}(\mathcal{A} \rightarrow \mathcal{T}) / \text{support}(\mathcal{T})\]
и усиление (leverage), которое отражает, насколько интересной может быть более высокая частота \(\mathcal{A}\) и \(\mathcal{T}\) в сочетании с более низким подъемом:
\[\text{leverage}(\mathcal{A} \rightarrow \mathcal{T}) = \text{support}(\mathcal{A} \rightarrow \mathcal{T}) - \text{support}(\mathcal{A})\times\text{support}(\mathcal{T})\]
Первый алгоритм поиска ассоциативных правил был разработан в 1993 г. сотрудниками исследовательского центра IBM, что сразу возбудило интерес к этому направлению. Каждый год появлялось несколько новых алгоритмов (DHP, Partition, DIC и др.), из которых наиболее известным остался алгоритм “Apriori” (Agrawal, Srikant, 1994).
Пакет arules позволяет находить часто встречающиеся сочетания элементов в данных (frequent itemsets) и отбирать ассоциативные правила, обеспечивая интерфейс к модулям на языке C, которые реализуют алгоритмы “Apriori” и “Eclat”. Так как обычно обрабатываются большие множества наборов и правил, то для уменьшения объёмов требуемой памяти пакет содержит развитый инструментарий преобразования разреженных входных матриц в компактные наборы транзакций (Hahsler et al., 2016; Огнева, 2012).
Для реализации работы с алгоритмами выделения ассоциаций в arules реализованы специальные типы данных, относящиеся к объектам трех классов: входной массив транзакций (transactions) и на выходе - часто встречающиеся фрагменты данных (itemsets) и правила (rules).
Объекты класса transactions представляют собой специально организованные бинарные матрицы со строками-наборами и столбцами-признаками, содержащие значения элемента 1, если соответствующий признак есть в транзакции, и 0, если он отсутствует. В зависимости от типа данных и способа их загрузки, эти объекты могут иметь разные способы организации и состав дополнительных слотов. В частности, подкласс itemMatrix является одновременно средством представления разреженных матриц с использованием функционала пакета Matrix. Другим способом формирования экземпляров класса transactions является загрузка данных из файла функцией read.transactions().
Для выделения ассоциативных правил вновь обратимся к нашему примеру по классификации лиц избирателей (см. рис. 5.1). Метод "basket" функции read.transactions() предполагает, что каждая строка в файле представляет собой одну транзакцию, в которой признаки (т.е. их метки) разделены символами sep (по умолчанию - запятая). Переформируем исходную таблицу данных в файл необходимого формата:
DFace <- read.delim(file = "data/Faces.txt",
header = TRUE, row.names = 1)
Class <- DFace$Class
DFaceN <- DFace[, -17]
colnames(DFaceN) <- c("голова_круглая", "уши_оттопырен",
"нос_круглый", "глаза_круглые", "лоб_морщины",
"носогубн_складка", "губы_толстые", "волосы",
"усы", "борода", "очки", "родинка_щеке", "бабочка",
"брови_подняты", "серьга", "курит_трубка")
Class[Class == 1] <- "Патриот"
Class[Class == 2] <- "Демократ"
items_list <- sapply(1:nrow(DFaceN), function(i)
paste(c(Class[i], colnames(DFaceN[i, DFaceN[i, ] == 1])),
collapse = ",", sep = "\n"))
head(items_list)## [1] "Патриот,уши_оттопырен,лоб_морщины,носогубн_складка,усы,борода,очки,бабочка,брови_подняты,курит_трубка"
## [2] "Патриот,голова_круглая,нос_круглый,глаза_круглые,губы_толстые,волосы,борода,очки,родинка_щеке,серьга"
## [3] "Патриот,глаза_круглые,лоб_морщины,носогубн_складка,волосы,усы,очки,родинка_щеке,бабочка,курит_трубка"
## [4] "Патриот,уши_оттопырен,нос_круглый,носогубн_складка,губы_толстые,борода,очки,брови_подняты,серьга,курит_трубка"
## [5] "Патриот,голова_круглая,уши_оттопырен,глаза_круглые,носогубн_складка,волосы,борода,родинка_щеке,брови_подняты,серьга"
## [6] "Патриот,нос_круглый,лоб_морщины,носогубн_складка,губы_толстые,усы,очки,бабочка,серьга,курит_трубка"write(items_list, file = "data/face_basket.txt")Загрузим данные из файла и создадим объект itemMatrix. Информацию о сформированном массиве транзакций можно получить, выполнив команды inspect() и summary().
library(arules)
trans <- read.transactions("data/face_basket.txt",
format = "basket", sep = ",")inspect(trans) # Выводимые данные не показаныsummary(trans)## transactions as itemMatrix in sparse format with
## 16 rows (elements/itemsets/transactions) and
## 18 columns (items) and a density of 0.5555556
##
## most frequent items:
## бабочка брови_подняты глаза_круглые борода губы_толстые
## 10 10 10 10 10
## (Other)
## 110
##
## element (itemset/transaction) length distribution:
## sizes
## 10
## 16
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 10 10 10 10 10 10
##
## includes extended item information - examples:
## labels
## 1 бабочка
## 2 Демократ
## 3 брови_поднятыДля объектов класса itemMatrix можно осуществить быструю визуализацию данных или построить график распределения частот встречаемости признаков (рис. 5.4).
image(trans)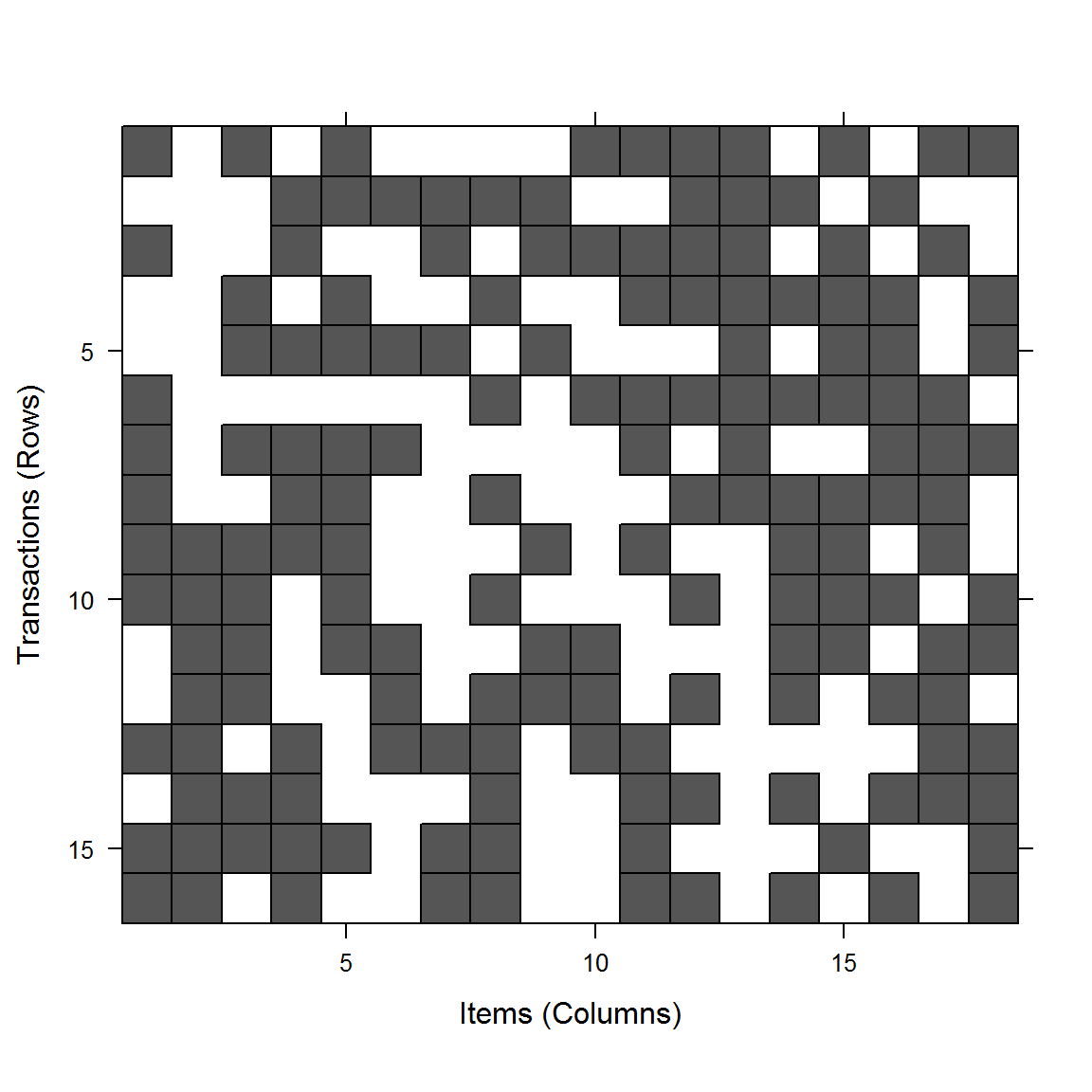
itemFrequencyPlot(trans, support = 0.1, cex.names = 0.8)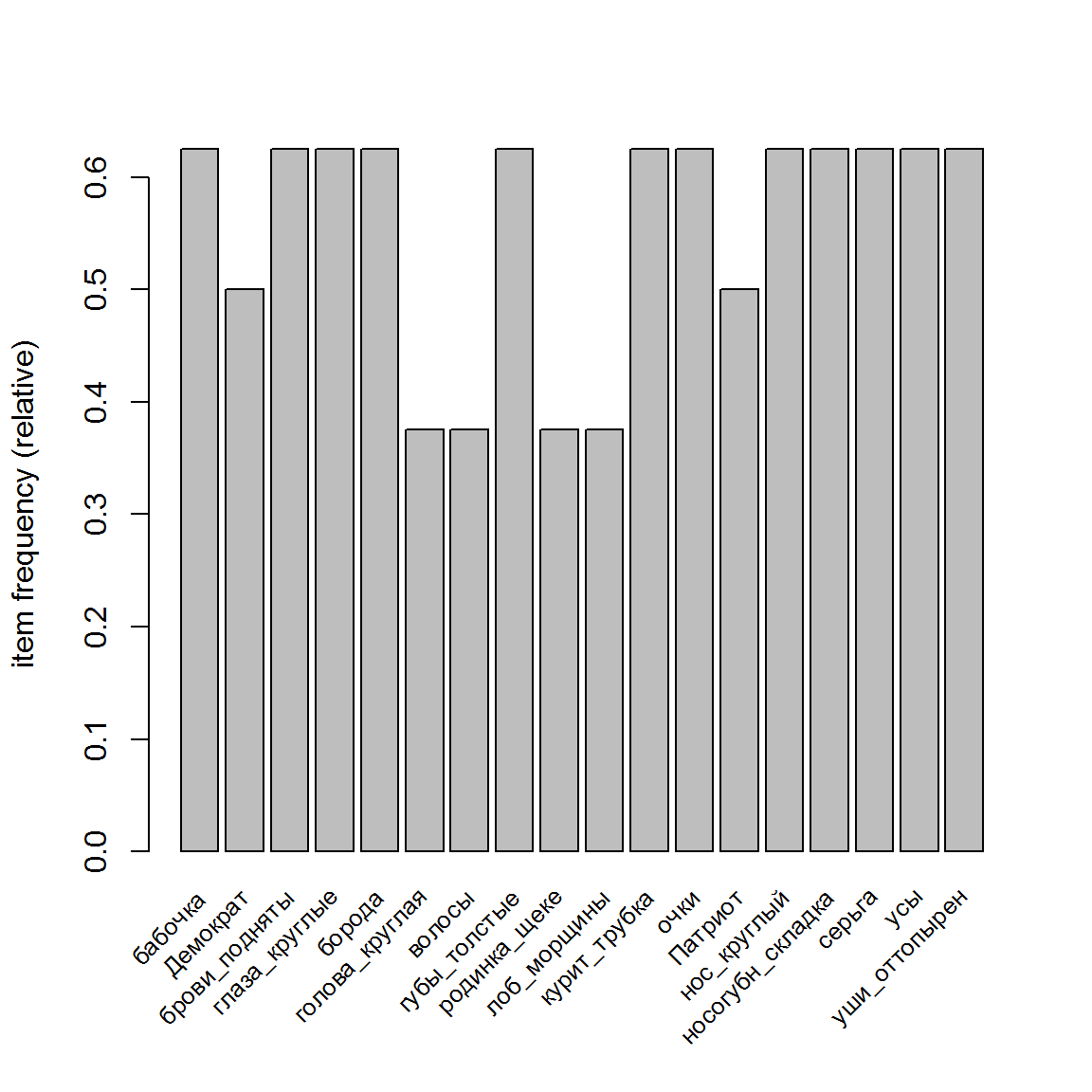
Рисунок 5.4: Матрица признаки/транзакции и частотное распределение встречаемости признаков в транзакциях
Поиск ассоциативных правил является не вполне тривиальной задачей, т.к. с ростом числа элементов в \(\mathbf{A}\) экспоненциально растет число их потенциальных комбинаций. Алгоритм “Apriori” является итерационным, при этом сначала выполняются действия для одноэлементных наборов, затем для 2-х, 3-х элементных и т.д. (т.е. он во многом напоминает алгоритм “Кора”).
На первом шаге первой итерации алгоритма подсчитываются одноэлементные часто встречающиеся наборы. Для этого необходимо пройтись по всему массиву данных и подсчитать для них поддержку, т.е. сколько раз набор встречается в имеющемся наборе данных. При последующем поиске \(k\)-элементных наборов генерация претендентов состоит из двух фаз - формирование кандидатов нового уровня на основе \((k - 1)\)-элементных наборов, которые были определены на предыдущей итерации алгоритма, и удаление избыточных кандидатов. После того как найдены все часто встречающиеся наборы элементов, выполняют процедуру непосредственного извлечения правил из построенного хеш-дерева (Зайцев, 2009).
Результатом анализа транзакций с помощью пакета arules являются объекты класса associations, включающие описания множества отношений между признаками (в виде часто встречающихся фрагментов, или правил), которые отбираются в соответствии с различными перечисленными выше мерами качества. Подкласс rules состоит из двух объектов itemMatrix, представляющих левую lhs (left-hand-side) и правую rhs (right-hand-side) сторону правила \(\mathcal{A} \rightarrow \mathcal{T}\), т.е. \(\mathcal{A}\) - lhs, \(\mathcal{T}\) - rhs.
Формирование правил осуществляется функцией apriori() с указанием пороговых значений поддержки и достоверности. Функция summary() обеспечивает частотный анализ правил по их длине и достигнутым мерам качества:
rules <- apriori(trans,
parameter = list(support = 0.01, confidence = 0.6))## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.6 0.1 1 none FALSE TRUE 5 0.01 1
## maxlen target ext
## 10 rules FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 0
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[18 item(s), 16 transaction(s)] done [0.00s].
## sorting and recoding items ... [18 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 7 8 9 10 done [0.00s].
## writing ... [48306 rule(s)] done [0.01s].
## creating S4 object ... done [0.02s].summary(rules) # Результаты показаны частично## set of 48306 rules
##
## rule length distribution (lhs + rhs):sizes
## 1 2 3 4 5 6 7 8 9 10
## 12 138 916 3892 9860 14560 11814 5526 1428 160
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.00 5.00 6.00 6.14 7.00 10.00
##
## summary of quality measures:
## support confidence lift
## Min. :0.06250 Min. :0.6000 Min. :0.960
## 1st Qu.:0.06250 1st Qu.:1.0000 1st Qu.:1.600
## Median :0.06250 Median :1.0000 Median :1.600
## Mean :0.07788 Mean :0.9781 Mean :1.750
## 3rd Qu.:0.06250 3rd Qu.:1.0000 3rd Qu.:1.600
## Max. :0.62500 Max. :1.0000 Max. :2.667
##
## mining info:
## data ntransactions support confidence
## trans 16 0.01 0.6Всего было отобрано 48306 правил, длина которых большей частью составляла от 5 до 7 элементов. Функция plot() из пакета arulesViz позволяет получать различные формы визуализации синтезированных правил, в том числе, анализ изменчивости их мер качества (рис. 5.5):
library(arulesViz)
plot(rules, measure = c("support", "lift"), shading = "confidence")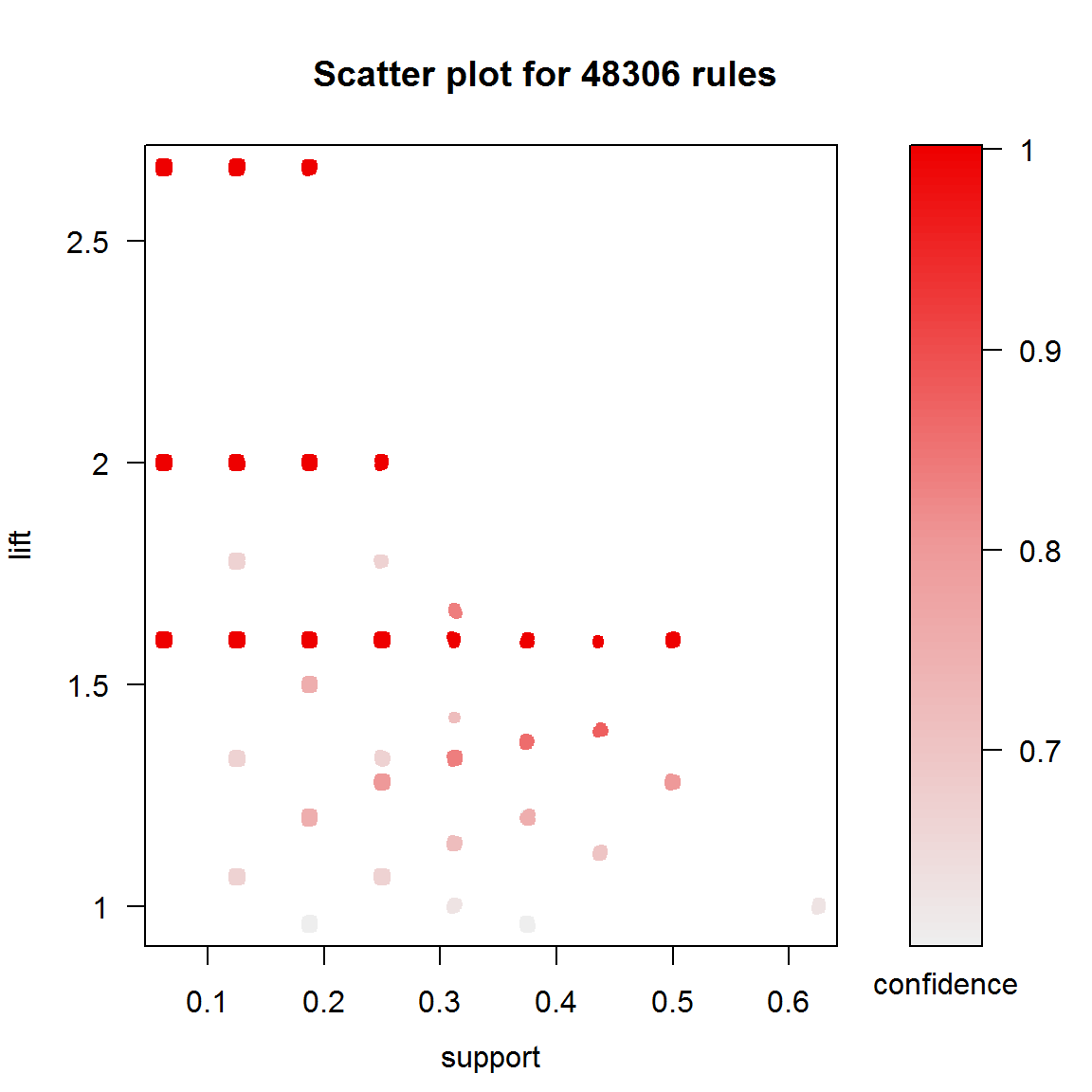
Рисунок 5.5: Поддержка, лифт и достоверность сгенерированных правил
Для решения задачи выявления характерных особенностей групп электората нас интересуют, в первую очередь, высококачественные правила, имеющие соответствующий признак группы в правой части. Тогда патриотов можно будет легко узнать по их облику (рис. 5.6):
rulesPat <- subset(rules,
subset = rhs %in% "Патриот" & lift > 1.8)
inspect(head(rulesPat, n = 10, by = "support"))## lhs rhs support confidence lift
## [1] {глаза_круглые,
## борода,
## серьга} => {Патриот} 0.2500 1 2
## [2] {очки,
## носогубн_складка,
## усы} => {Патриот} 0.2500 1 2
## [3] {бабочка,
## очки,
## усы} => {Патриот} 0.2500 1 2
## [4] {курит_трубка,
## очки,
## носогубн_складка} => {Патриот} 0.2500 1 2
## [5] {бабочка,
## очки,
## носогубн_складка,
## усы} => {Патриот} 0.2500 1 2
## [6] {волосы,
## родинка_щеке} => {Патриот} 0.1875 1 2
## [7] {лоб_морщины,
## очки,
## носогубн_складка} => {Патриот} 0.1875 1 2
## [8] {лоб_морщины,
## курит_трубка,
## носогубн_складка} => {Патриот} 0.1875 1 2
## [9] {бабочка,
## лоб_морщины,
## носогубн_складка} => {Патриот} 0.1875 1 2
## [10] {лоб_морщины,
## курит_трубка,
## очки} => {Патриот} 0.1875 1 2plot(head(sort(rulesPat, by = "support"), 10),
method = "paracoord")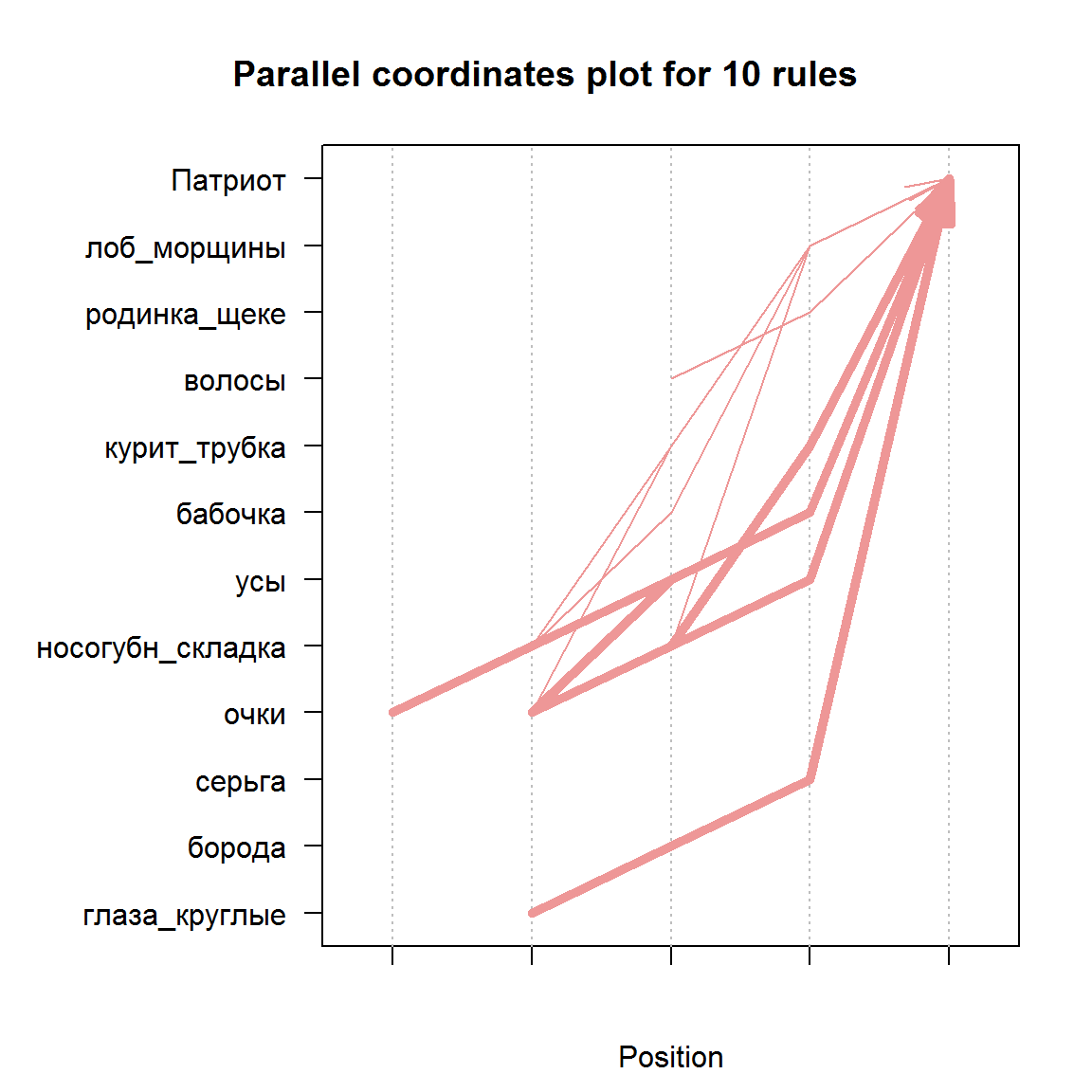
Рисунок 5.6: График 10 лучших правил для патриотов в параллельных координатах
График в параллельных координатах (method="paracoord") на рис. 5.6 показывает, как формируются комбинации признаков правой части при увеличении ее размера, а толщина линий соответствует уровню поддержки.
Аналогичные правила могут быть отобраны для группы демократично настроенных избирателей (рис. 5.7):
rulesDem <- subset(rules, subset = rhs %in% "Демократ" & lift > 1.8)
inspect(head(rulesDem, n = 10, by = "support"))## lhs rhs support confidence lift
## [1] {брови_подняты,
## нос_круглый,
## усы} => {Демократ} 0.2500 1 2
## [2] {глаза_круглые,
## губы_толстые,
## уши_оттопырен} => {Демократ} 0.2500 1 2
## [3] {глаза_круглые,
## губы_толстые,
## курит_трубка} => {Демократ} 0.2500 1 2
## [4] {бабочка,
## губы_толстые,
## уши_оттопырен} => {Демократ} 0.2500 1 2
## [5] {глаза_круглые,
## губы_толстые,
## курит_трубка,
## уши_оттопырен} => {Демократ} 0.2500 1 2
## [6] {голова_круглая,
## лоб_морщины} => {Демократ} 0.1875 1 2
## [7] {голова_круглая,
## лоб_морщины,
## усы} => {Демократ} 0.1875 1 2
## [8] {родинка_щеке,
## нос_круглый,
## усы} => {Демократ} 0.1875 1 2
## [9] {брови_подняты,
## родинка_щеке,
## нос_круглый} => {Демократ} 0.1875 1 2
## [10] {брови_подняты,
## родинка_щеке,
## усы} => {Демократ} 0.1875 1 2plot(head(sort(rulesDem, by = "support"), 10), method = "graph",
control = list(nodeCol = grey.colors(10),
edgeCol = grey(.7), alpha = 1))
Рисунок 5.7: Визуализация в форме графа 10 лучших правил для демократов
Метод "graph" функции plot() показывает правила и составляющие их признаки в виде графа, размер узлов которого пропорционален уровню поддержки каждого представленного правила (рис. 5.7).