Классификация, регрессия и другие алгоритмы Data Mining с использованием R

4.3 Построение деревьев регрессии

Деревья решений (Breiman at al., 1984; Quinlan, 1986) осуществляют разбиение пространства объектов в соответствии с некоторым набором правил разбиения (splitting rule). Эти правила являются логическими утверждениями в отношении той или иной переменной и могут быть истинными или ложными. Ключевыми здесь являются три обстоятельства: а) правила позволяют реализовать последовательную дихотомическую сегментацию данных, б) два объекта считаются похожими, если они оказываются в одном и том же сегменте разбиения, в) на каждом шаге разбиения увеличивается количество информации относительно исследуемой переменной (отклика).

Деревья классификации и регрессии являются одним из наиболее популярных методов решения многих практических задач, что обусловлено следующими причинами:

Деревья решений позволяют получать очень легко интерпретируемые модели, представляющие собой набор правил вида “если…, то…”. Интерпретация облегчается, в том числе, за счет возможности представить эти правила в виде наглядной древовидной структуры.
В силу своего устройства деревья решений позволяют работать с переменными любого типа без необходимости какой-либо предварительной подготовки этих переменных для ввода в модель (например, логарифмирование, преобразование категориальных переменных в индикаторные, и т.п.).
Исследователю нет необходимости в явном виде задавать форму взаимосвязи между откликом и предикторами, как это, например, происходит в случае с обычными регрессионными моделями. Это оказывается особенно полезным при работе с данными большого объема, о свойствах которых мало что известно.
Деревья решений, по сути, автоматически выполняют отбор информативных предикторов и учитывают возможные взаимодействия между ними. Это, в частности, делает деревья решений полезным инструментом разведочного анализа данных.
Деревья решений можно эффективно применять к данным с пропущенными значениями, что очень полезно при решении практических задач, где наличие пропущенных значений – это, скорее, правило, чем исключение.
Деревья решений одинаково хорошо применимы как к количественным, так и к качественным зависимым переменным.

К недостаткам этого класса моделей иногда относят нестабильность и невысокую точность предсказаний, что, как будет показано ниже, не всегда подтверждается. По своей сути, деревья используют “наивный подход” (naive approach) в том смысле, что они исходят из предположения о взаимной независимости признаков. Поэтому модели регрессионных деревьев статистически наиболее работоспособны, когда комплекс анализируемых переменных является не слишком мультиколлинеарным или имеется регулярная внутренняя множественная альтернатива в исходной комбинации признаков.

Алгоритм CART (Classification and Regression Tree) рекурсивно делит исходный набор данных на подмножества, которые становятся все более и более гомогенными относительно определенных признаков, в результате чего формируется древовидная иерархическая структура. Деление осуществляется на основе традиционных логических правил в виде ЕСЛИ (А) ТО (В), где А - некоторое логическое условие, а В - процедура деления подмножества на две части, для одной из которых условие А истинно, а для другой - ложно. Примеры условий: Xi==F, Хi <= V; Хi >= V и др., где Хi – один из предикторов исходной таблицы, F - выбранное значение категориальной переменной, V - специально подобранное опорное значение (порог).

На первой итерации корневой узел дерева связывается с наиболее оптимальным условным суждением, и все множество объектов делится на две группы. От каждого последующего узла-родителя к узлам-потомкам также может отходить по две ветви, в свою очередь связанные c граничными значениями других наиболее подходящих переменных и определяющие правила дальнейшего разделения (splitting criterion). Конечными узлами дерева являются “листья”, соответствующие найденным решениям и объединяющие все разделенные на группы объекты обучающей выборки. Общее правило выбора опорного значения для каждого узла построенного дерева можно сформулировать следующим образом: “выбранный признак должен разбить множество \(\mathbf{X}^*\) так, чтобы получаемые в итоге подмножества \(\mathbf{X}_k^*, k = 1, 2, \dots, p\), состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому”.

Описанный процесс относится к так называемым “жадным” алгоритмам, стремящимся, не считаясь ни с чем, построить максимально “кустистое” дерево (также “глубокое дерево”, deep tree). Естественно, чем обширнее и кустистее дерево, тем лучше будут результаты его тестирования на обучающей выборке, но не столь успешными – на проверочной выборке. Поэтому построенная модель должна быть еще и оптимальной по размерам, т.е. содержать информацию, улучшающую качество распознавания, и игнорировать ту информацию, которая его не улучшает. Для этого обычно проводят “обрезание” дерева (tree pruning) – отсечение ветвей там, где эта процедура не приводит к серьезному возрастанию ошибки.

Невозможно подобрать объективный внутренний критерий, приводящий к хорошему компромиссу между безошибочностью и компактностью, поэтому стандартный механизм оптимизации деревьев основан на перекрестной проверке (Loh, Shih, 1997). Для этого обучающая выборка разделяется, например, на 10 равных частей: 9 частей используется для построения дерева, а оставшаяся часть играет роль проверочной совокупности. После многократного повторения этой процедуры из некоторого набора деревьев-претендентов, у которых имеется практически допустимый разброс критериев качества модели, выбирается дерево, показавшее наилучший результат при перекрестной проверке.

4.3.1 Построение деревьев на основе рекурсивного разбиения

В общем случае может быть использовано несколько алгоритмов построения деревьев на основе различных схем и критериев оптимизации. Функция rpart() из одноименного пакета выполняет рекурсивный выбор для каждого следующего узла таких разделяющих значений, которые приводят к минимальной сумме квадратов внутригрупповых отклонений Dt для всех t узлов дерева. Для оценки качества построенного дерева \(\mathbf{T}\) в ходе его оптимизации используется следующая совокупность критериев:

штраф за сложность модели (cost complexity), включающий штрафной множитель за каждую неотсечённую ветвь \(СС(\mathbf{T} = \sum_t D_t + \lambda t)\);
девианс \(D_0\) для нулевого дерева (т.е. оценка изменчивости в исходных данных);
относительный параметр стоимости сложности \(Cp = \lambda / D_0\);
относительная ошибка обучения для дерева из \(t\) узлов \(REL_{er} = \sum_t D_t /D_0\);
ошибка перекрестной проверки (\(CV_{er}\)) с разбиением на 10 блоков, также отнесенная к девиансу нуль-дерева \(D_0\); \(CV_{er}\), как правило, больше, чем \(REL_{er}\);
стандартное отклонение (\(SE\)) ошибки перекрестной проверки.

Лучшим считается дерево, состоящее из такого количества ветвей \(t\), для которого сумма (\(CV_{er} + SE\)) является минимальной.

В качестве примера рассмотрим построение дерева CART, прогнозирующего обилие водорослей группы a1 в зависимости от гидрохимических показателей воды и условий отбора проб в различных водотоках (см. разделы 3.4 и 4.1-4.2). Используем сначала пакет rpart, для работы с которым обычно применяется двухшаговая процедура: функция rpart() устанавливает связи между зависимой и независимыми переменными и формирует бинарное дерево, а функция prun() выполняет обрезание лишних ветвей.

load(file = "algae.RData") # Загрузка таблицы algae - раздел 4.1

library(rpart)
(rt.a1 <- rpart(a1 ~ ., data = algae[, 1:12]))

## n= 200 
## 
## node), split, n, deviance, yval
##       * denotes terminal node
## 
##  1) root 200 90694.880 16.923500  
##    2) PO4>=43.818 148 31359.210  8.918919  
##      4) Cl>=7.8065 141 21678.580  7.439716  
##        8) oPO4>=51.118 85  3455.770  3.801176 *
##        9) oPO4< 51.118 56 15389.430 12.962500  
##         18) mnO2>=10.05 24  1248.673  6.716667 *
##         19) mnO2< 10.05 32 12502.320 17.646870  
##           38) NO3>=3.1875 9   257.080  7.866667 *
##           39) NO3< 3.1875 23 11047.500 21.473910  
##             78) mnO2< 8 13  2919.549 13.807690 *
##             79) mnO2>=8 10  6370.704 31.440000 *
##      5) Cl< 7.8065 7  3157.769 38.714290 *
##    3) PO4< 43.818 52 22863.170 39.705770  
##      6) mxPH< 7.87 28 11636.710 32.875000  
##       12) oPO4>=3.1665 14  1408.304 23.978570 *
##       13) oPO4< 3.1665 14  8012.309 41.771430 *
##      7) mxPH>=7.87 24  8395.785 47.675000  
##       14) PO4>=15.177 12  3047.517 38.183330 *
##       15) PO4< 15.177 12  3186.067 57.166670 *

Приведенной командой мы построили полное дерево без обрезания ветвей, состоящее из 9 узлов и 10 листьев, обозначенных в приведенном протоколе разбиения символом *. В каждой строке представлены по порядку: условие разделения, число наблюдений, соответствующих этому условию, девианс (в данном случае - это эквивалент суммы квадратов отклонений от группового среднего) и среднее значение отклика для выделенной ветви. Например, перед первой итерацией общее множество из 200 наблюдений имеет среднее значение m = 16.92 при девиансе D = 90694. При PO4>=43.8 это множество делится на две части: 2) 148 наблюдений (m =8.92, D = 31359) и 3) 52 наблюдения с высоким уровнем обилия водорослей (m =39.7, D = 22863). Дальнейшие разбиения каждой из этих двух частей аналогичны.

Разумеется, лучший вариант – представить дерево графически. Популярны три варианта визуализации с использованием различных функций: plot(), prettyTree() из пакета DMwR и prp() из чрезвычайно продвинутого пакета rpart.plot (рис. 4.7):

prettyTree(rt.a1)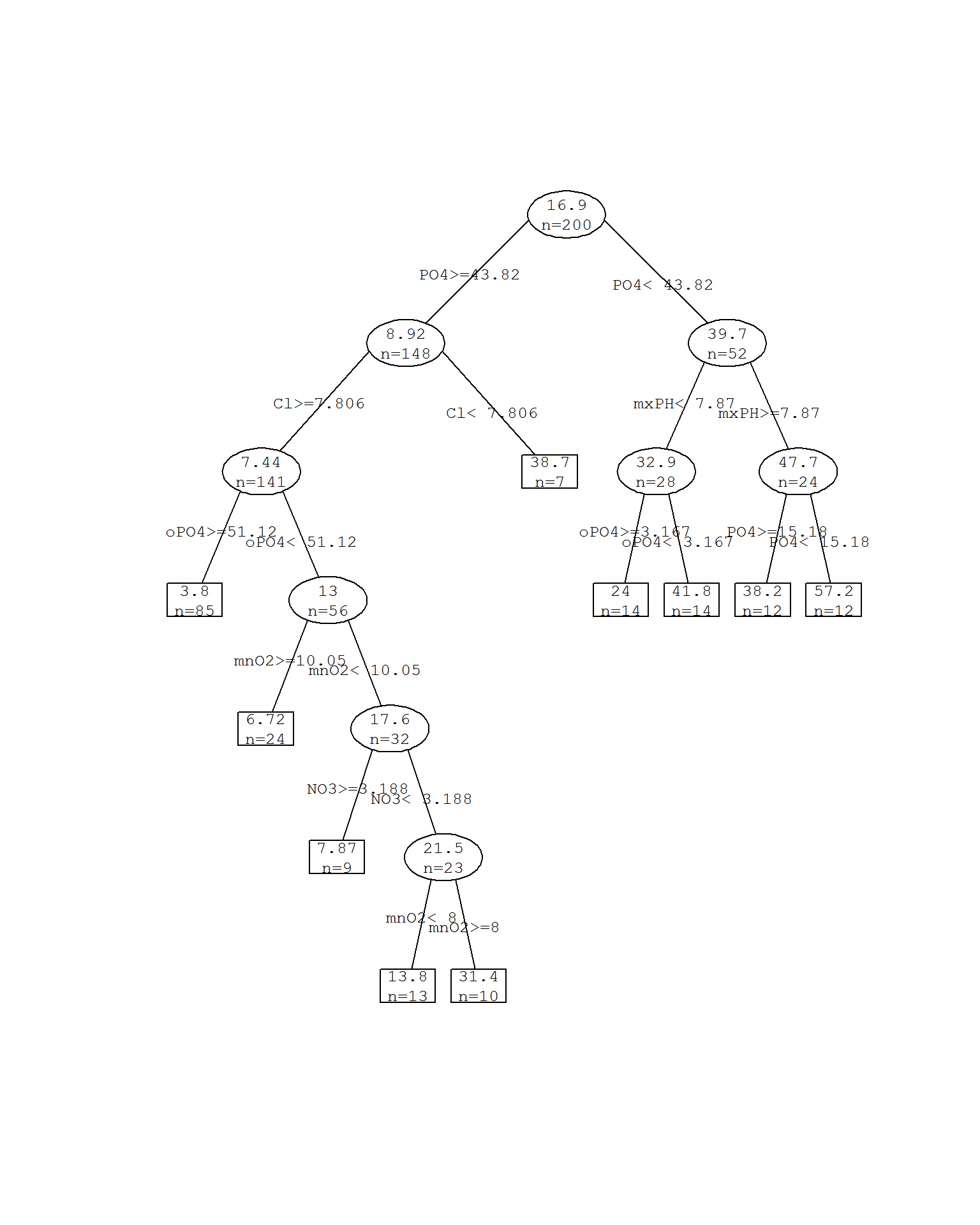

Рисунок 4.7: Дерево rpart без обрезания ветвей

Полезно также проследить изменение перечисленных выше статистических критериев по мере выращивания дерева:

printcp(rt.a1)

## 
## Regression tree:
## rpart(formula = a1 ~ ., data = algae[, 1:12])
## 
## Variables actually used in tree construction:
## [1] Cl   mnO2 mxPH NO3  oPO4 PO4 
## 
## Root node error: 90695/200 = 453.47
## 
## n= 200 
## 
##         CP nsplit rel error  xerror    xstd
## 1 0.402145      0   1.00000 1.00890 0.13049
## 2 0.071921      1   0.59785 0.71564 0.11458
## 3 0.031241      2   0.52593 0.68023 0.11225
## 4 0.031211      3   0.49469 0.71624 0.11875
## 5 0.024435      4   0.46348 0.70740 0.11725
## 6 0.023840      5   0.43905 0.69403 0.11063
## 7 0.018065      6   0.41521 0.70573 0.10933
## 8 0.016291      7   0.39714 0.74901 0.11225
## 9 0.010000      9   0.36456 0.78376 0.11720

Функция rpart() и другие функции из пакета rpart имеют собственные возможности выполнить перекрестную проверку и оценить ее ошибку при различных значениях штрафа за сложность модели cp (рис. 4.8):

set.seed(505) # для воспроизводимости примера
#   Снижаем порог штрафа за сложность с шагом .005
rtp.a1 <- rpart(a1 ~ ., data = algae[, 1:12], 
                control = rpart.control(cp = .005)) 
#  График зависимости относительных ошибок от числа узлов
plotcp(rtp.a1) 
with(rtp.a1, {lines(cptable[, 2] + 1, cptable[, 3], type = "b", col = "red")
    legend("topright", c("Ошибка обучения",
                         "Ошибка крос-проверки (CV)", "min(CV ошибка)+SE"),
           lty = c(1, 1, 2), col = c("red", "black", "black"), bty = "n") })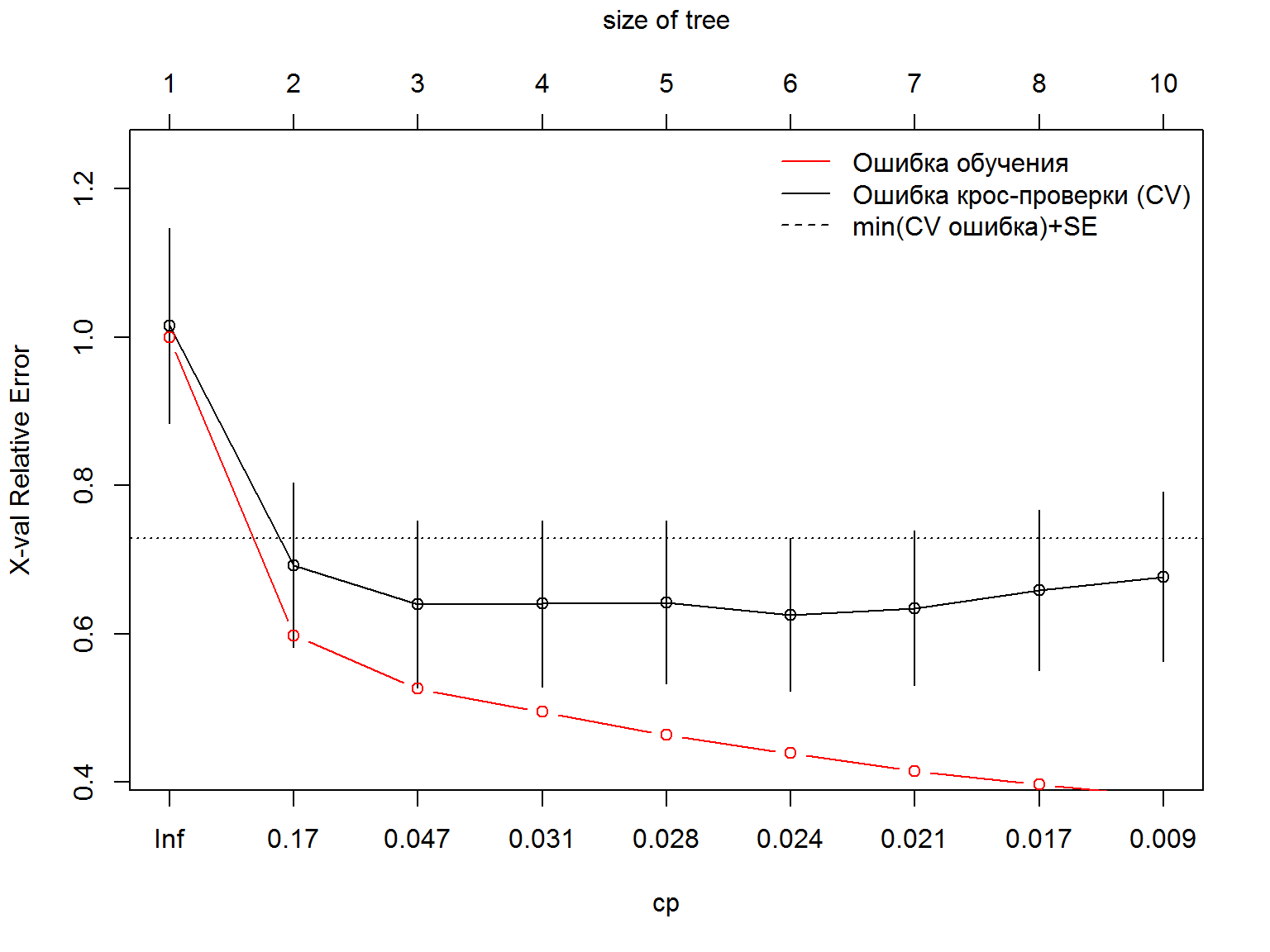

Рисунок 4.8: Зависимость относительной ошибки перекрестной проверки от штрафа за сложность модели cp

На рис. 4.8 видно, что минимум относительной ошибки при перекрестной проверке приходится на значение cp = 0.024.⁶ Выполним обрезку дерева при этом значении (рис. 4.9):

rtp.a1 <- prune(rtp.a1, cp = 0.024)
prettyTree(rtp.a1)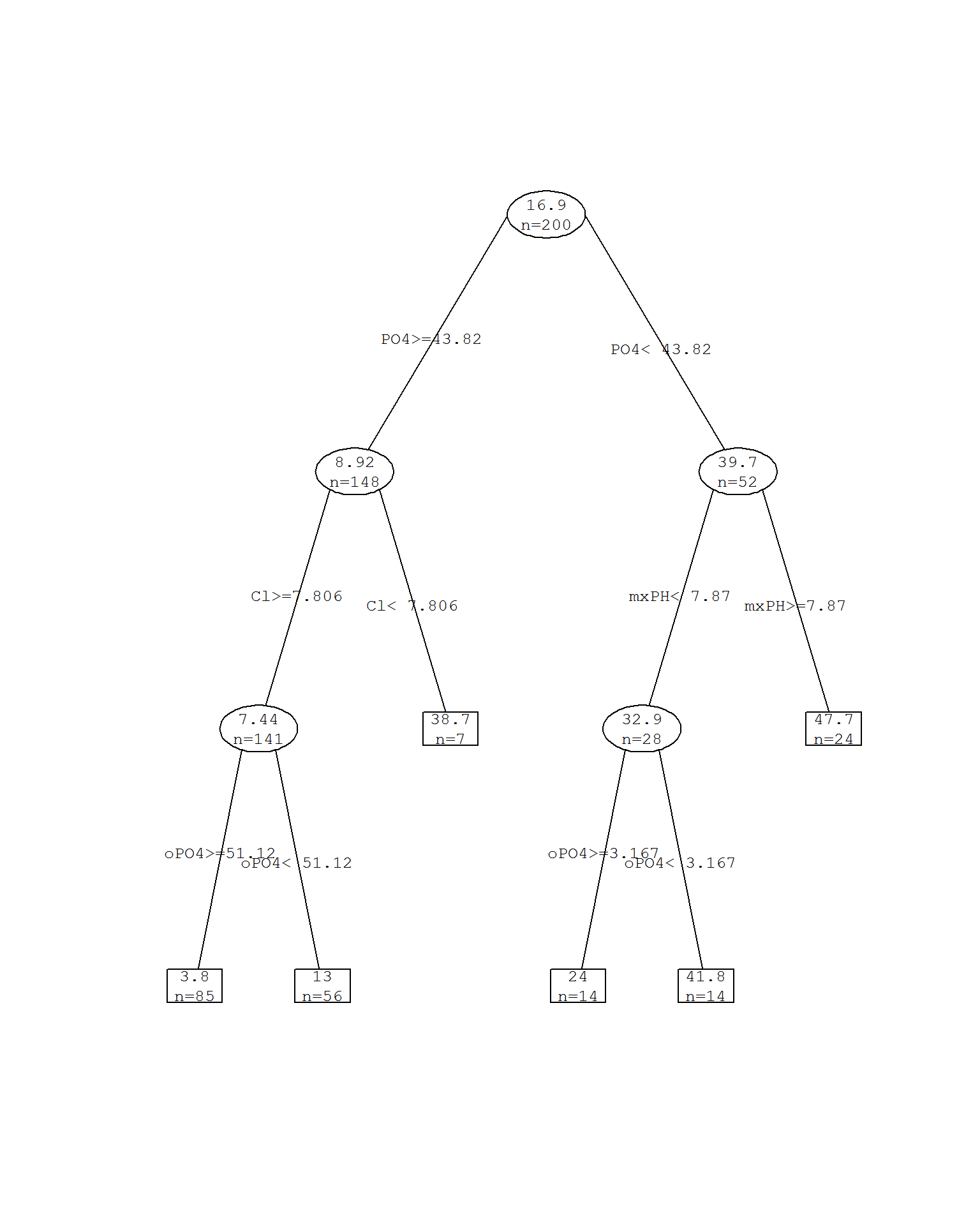

Рисунок 4.9: Дерево rpart c обрезанием ветвей при cp = 0.024

Выполним теперь дополнительную оптимизацию параметра ср с использованием функции train() из пакета caret (см раздел 3.5). Будем тестировать деревья регрессии при 30 значениях критерия ср, для каждого из которых выполним 10-кратную перекрестную проверку с 3 повторностями (рис. 4.10):

library(caret)
cvCtrl <- trainControl(method = "repeatedcv", repeats = 3)
set.seed(202) # для воспроизводимости примера
rt.a1.train <- train(a1 ~ ., data = algae[, 1:12], 
                     method = "rpart", tuneLength = 30, trControl = cvCtrl)
plot(rt.a1.train)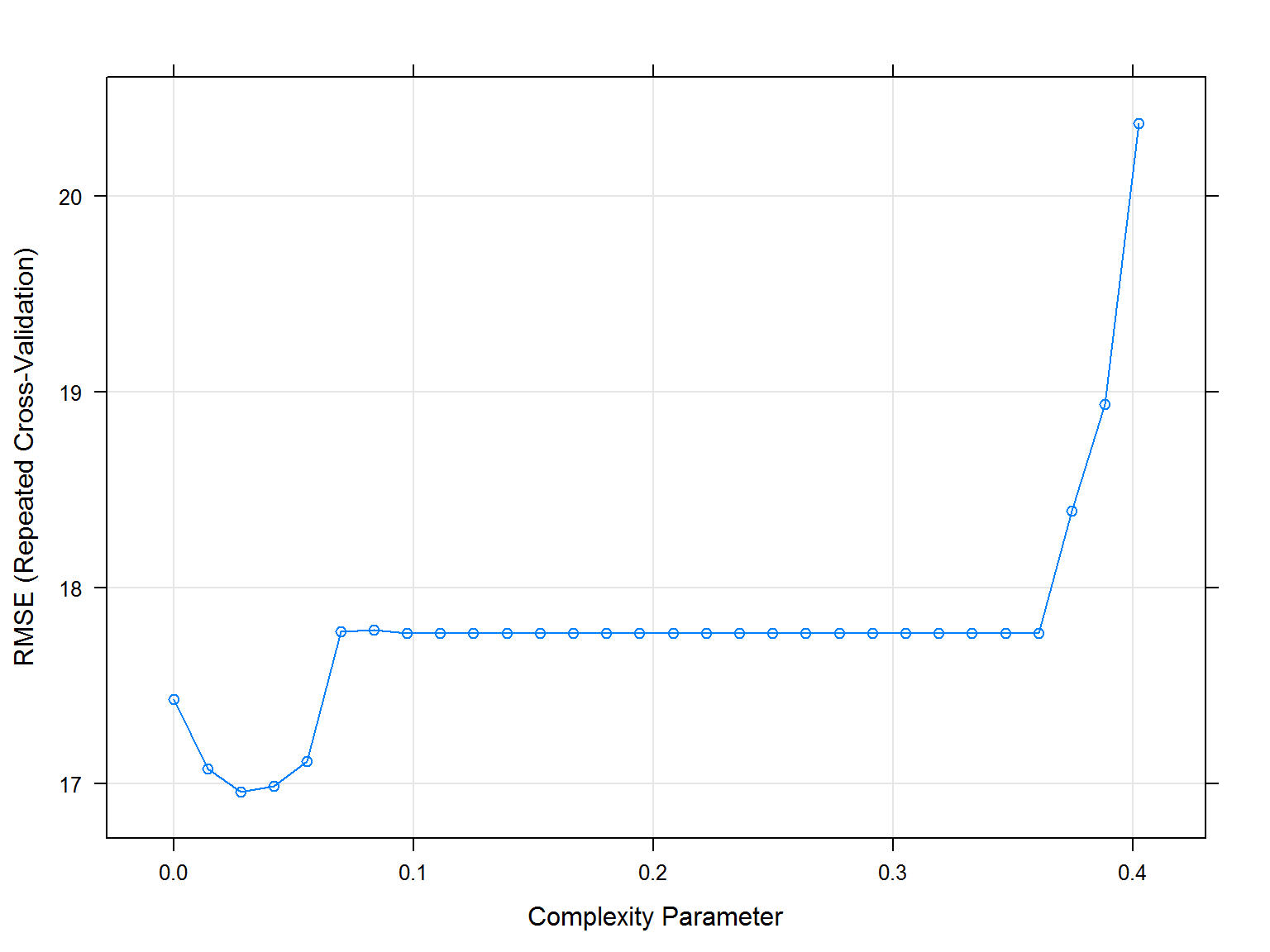

Рисунок 4.10: Оценка параметра cp с использованием функции train()

rtt.a1 <- rt.a1.train$finalModel
prettyTree(rtt.a1)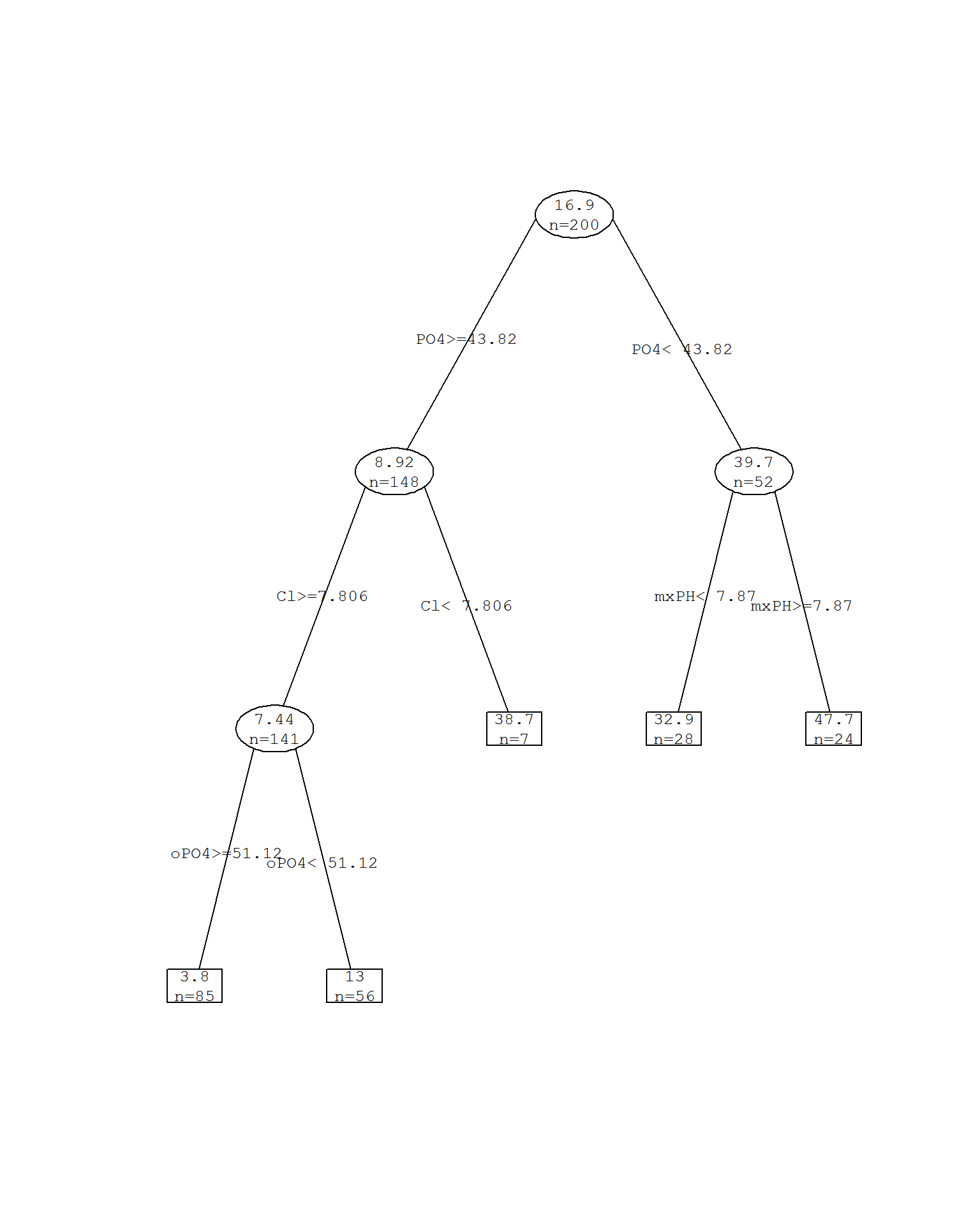

Рисунок 4.11: Дерево rpart c обрезанием ветвей при cp = 0.0277

При cp = 0.0277 было получено существенно урезанное дерево, которое, правда, значительно потеряло в своей объясняющей ценности.

4.3.2 Построение деревьев с использованием алгортма условного вывода

Обратимся теперь к принципиально другим методам рекурсивного разделения при построении деревьев, представленным в пакете party. Стандартный механизм проверки статистического гипотез, который предотвращает переусложнение модели, реализован в функции ctree(), использующей метод построения деревьев на основе “условного вывода” (conditional inference). Алгоритм принимает во внимание характер распределения отдельных переменных и осуществляет на каждом шаге рекурсивного разделения данных несмещенный выбор влияющих ковариат, используя формальный тест на основе статистического критерия \(c(\boldsymbol{t}_j, \mu_j, \Sigma_j), j = 1, \dots, m\), где \(\mu, \Sigma\) - соответственно среднее и ковариация (Hothorn et al., 2006). Оценка статистической значимости \(с\)-критерия выполняется на основе перестановочного теста, в результате чего формируются компактные деревья, не требующие процедуры обрезания.

library(party)  # Построение дерева методом "условного вывода"
(ctree.a1 <- ctree(a1 ~ ., data = algae[, 1:12]))

## 
##   Conditional inference tree with 4 terminal nodes
## 
## Response:  a1 
## Inputs:  season, size, speed, mxPH, mnO2, Cl, NO3, NH4, oPO4, PO4, Chla 
## Number of observations:  200 
## 
## 1) PO4 <= 43.5; criterion = 1, statistic = 47.106
##   2)*  weights = 52 
## 1) PO4 > 43.5
##   3) oPO4 <= 51.111; criterion = 0.985, statistic = 10.234
##     4) size == {small}; criterion = 0.993, statistic = 14.65
##       5)*  weights = 14 
##     4) size == {large, medium}
##       6)*  weights = 49 
##   3) oPO4 > 51.111
##     7)*  weights = 85

plot(ctree.a1)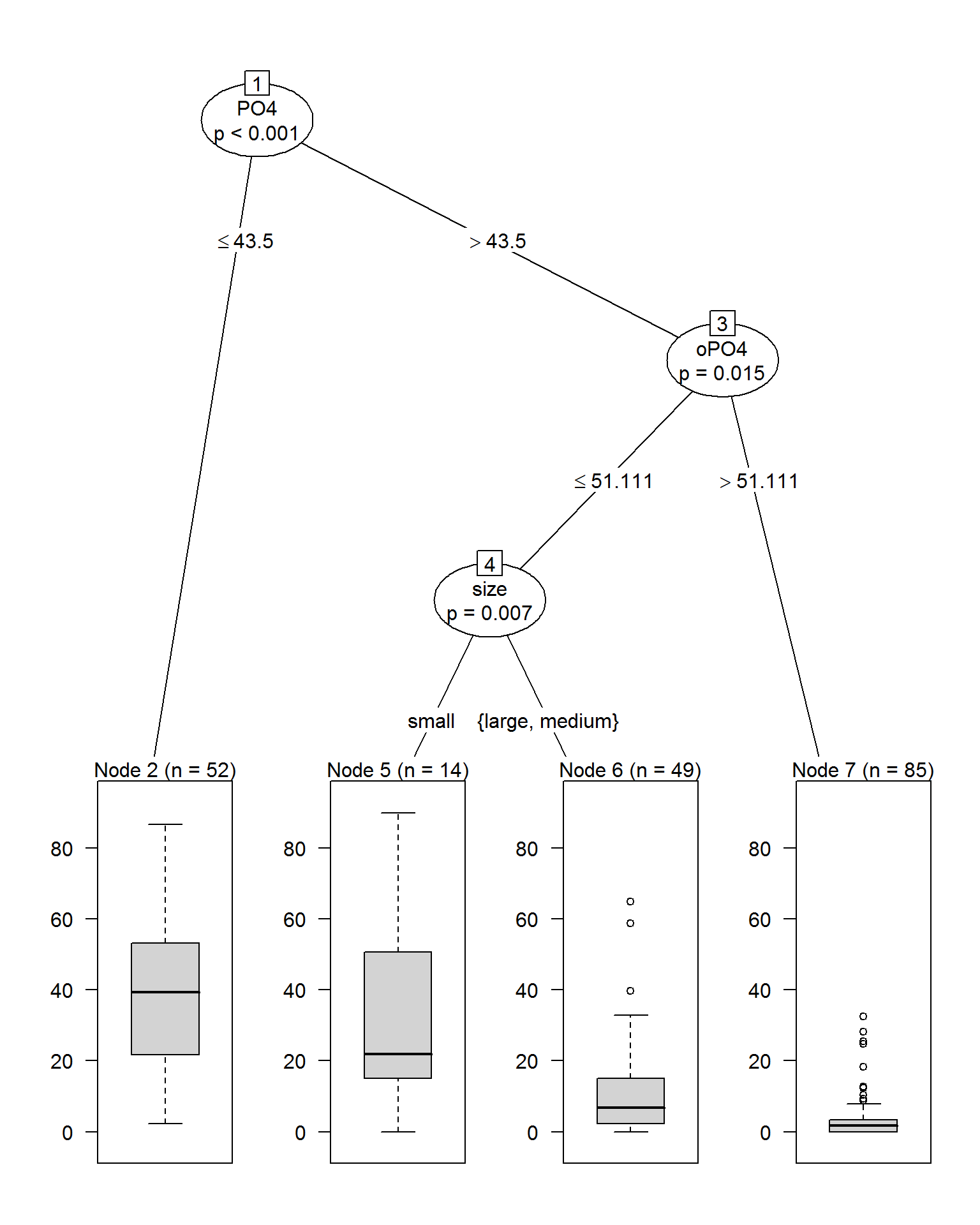

Рисунок 4.12: Дерево cpart без оптимизации параметра mincriterion

Оптимизацию параметра mincriterion выполним с использованием функции train() при тех же условиях перекрестной проверки:

ctree.a1.train <- train(a1 ~ ., data = algae[, 1:12], 
                        method = "ctree", tuneLength = 10, trControl = cvCtrl)
ctreet.a1 <- ctree.a1.train$finalModel
plot(ctreet.a1)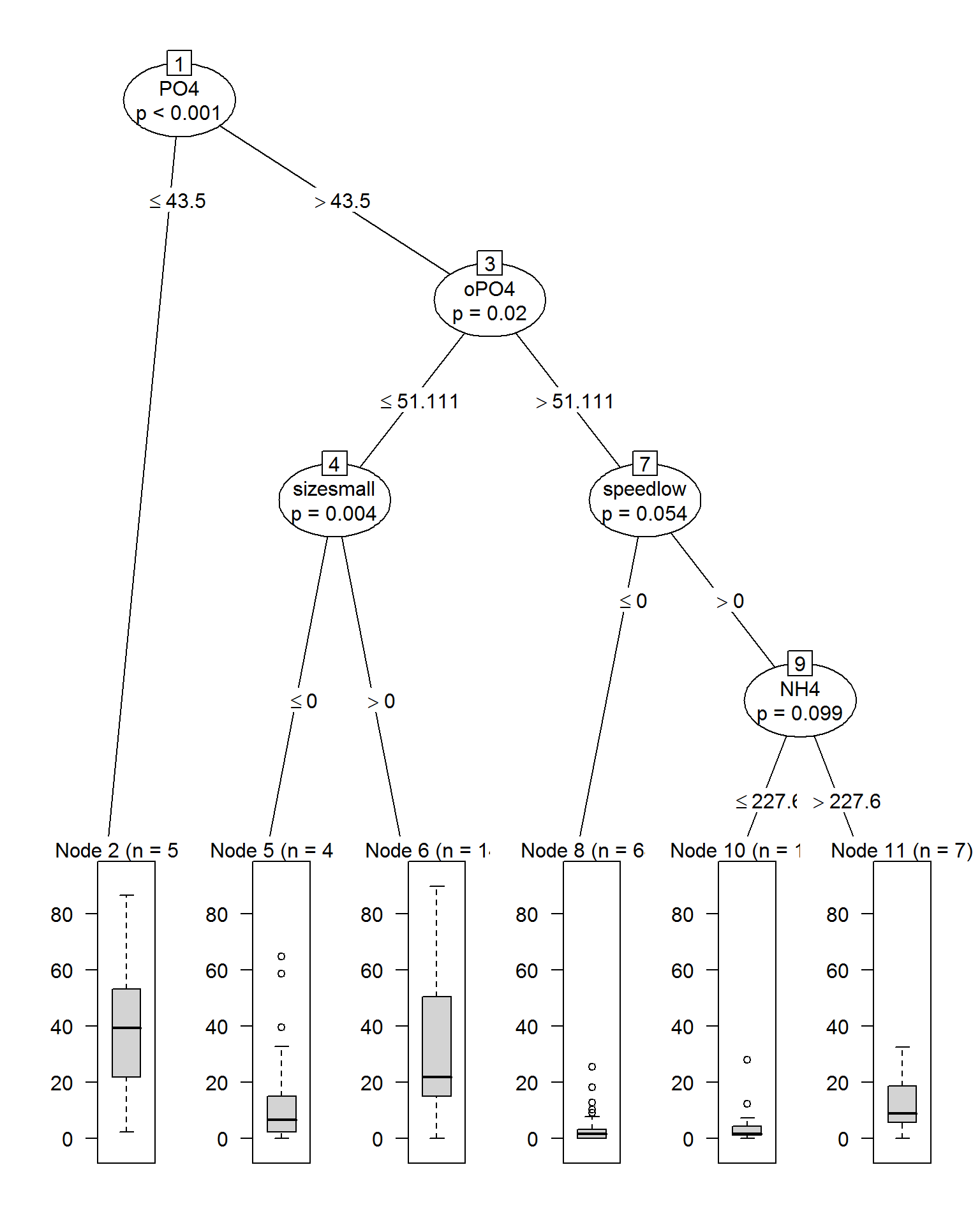

Рисунок 4.13: Дерево cpart после оптимизации параметра mincriterion

Здесь имел место обратный процесс: число узлов дерева было предложено увеличить с 7 до 11. Обратим также внимание на то, что в дереве появились категориальные переменные (размер и скорость течения реки), которые были проигнорированы rpart-деревьями.

4.3.3 Тестирование моделей с использованием дополнительного набора данных

Используем для прогноза набор данных (Torgo, 2011) из 140 наблюдений, который мы уже применяли в предыдущем разделе. Данные с восстановленными пропущенными значениями мы сохранили ранее в файле algae_test.RData (см раздел 4.1).

Оценим точность каждой модели на этом наборе данных по трем показателям: среднему абсолютному отклонению (MAE), корню из среднеквадратичного отклонения (RSME) и квадрату коэффициента детерминации Rsq = 1 - NSME, где NSME - относительная ошибка, равная отношению средних квадратов отклонений от модельных значений и от общего среднего:

load(file = "algae_test.RData") # Загрузка таблиц Eval, Sols

# Функция, выводящая вектор критериев
ModCrit <- function(pred, fact) {
    mae <- mean(abs(pred - fact))
    rmse <- sqrt(mean((pred - fact)^2))
    Rsq <- 1 - sum((fact - pred)^2)/sum((mean(fact) - fact)^2)
    c(MAE = mae, RSME = rmse, Rsq = Rsq) 
} 
Result <- rbind(
    rpart_prune = ModCrit(predict(rtp.a1, Eval), Sols[, 1]),
    rpart_train = ModCrit(predict(rt.a1.train, Eval), Sols[, 1]),
    ctree_party = ModCrit(predict(ctree.a1, Eval), Sols[, 1]),
    ctree_train = ModCrit(predict(ctree.a1.train, Eval), Sols[, 1])
)
Result

##                  MAE     RSME       Rsq
## rpart_prune 10.99017 15.72931 0.4105428
## rpart_train 11.13198 16.04396 0.3867241
## ctree_party 11.31029 16.52534 0.3493711
## ctree_train 11.47503 16.63481 0.3407221

Можно с разумной осторожностью сделать вывод о том, что деревья, построенные rpart(), немного точнее, чем деревья условного вывода ctree(). При этом все деревья решений оказались существенно эффективней для прогнозирования свежих данных, чем все ранее построенные модели.

Обратите внимание: в связи с небольшим объемом рассматриваемого набора данных, оптимальные значения cp, найденные по результатам перекрестной проверки, будут существенно варьировать от раза к разу. Так, используя другое значение зерна в команде set.seed() вы, скорее всего, получите другое “оптимальное” значение сp.↩