4.2 Регуляризация, частные наименьшие квадраты и kNN-регрессия
4.2.1 Регрессия по методу “лассо”
Регрессия по методу наименьших квадратов (МНК) часто может стать неустойчивой, то есть сильно зависящей от обучающих данных, что обычно является проявлением тенденции к переобучению. Избежать такого переобучения помогает регуляризация - общий метод, заключающийся в наложении дополнительных ограничений на искомые параметры, которые могут предотвратить излишнюю сложность модели. Смысл процедуры заключается в “стягивании” в ходе настройки вектора коэффициентов \(\boldsymbol{\beta}\) таким образом, чтобы они в среднем оказались несколько меньше по абсолютной величине, чем это было бы при оптимизации по МНК.
Метод регрессии “лассо” (LASSO, Least Absolute Shrinkage and Selection Operator) заключается во введении дополнительного слагаемого регуляризации в функционал оптимизации модели, что часто позволяет получать более устойчивое решение. Условие минимизации квадратов ошибки при оценке параметров \(\hat{\beta}\) выражается следующей формулой: \[\hat{\beta} = \arg \min \left(\sum_{i=1}^n (y_i - \sum_{j=1}^m \beta_j x_{ij})^2 + \lambda |\boldsymbol{\beta}|\right),\]
где \(\lambda\) - параметр регуляризации, имеющий смысл штрафа за сложность.
При этом достигается некоторый компромисс между ошибкой регрессии и размерностью используемого признакового пространства, выраженного суммой абсолютных значений коэффициентов \(|\boldsymbol{\beta}|\). В ходе минимизации некоторые коэффициенты становятся равными нулю, что, собственно, и определяет отбор информативных признаков.
При значении параметра регуляризации \(\lambda = 0\), лассо-регрессия сводится к обычному методу наименьших квадратов, а при увеличении \(\lambda\) формируемая модель становится все более “лаконичной”, пока не превратится в нуль-модель. Оптимальная величина \(\lambda\) находится с использованием перекрестной проверки, т.е. ей соответствует минимальная ошибка прогноза \(\hat{y}_i\) на наблюдениях, не участвовавших в построении самой модели.
Обобщением регрессии с регуляризацией можно считать модель “эластичных сетей” (elastic net - Zou, Hastie, 2005). Эта модель устанавливает сразу два типа штрафных параметров - \(\lambda_1\) и \(\lambda_2\), объединяет гребневую регрессию (при \(\lambda_2 = 0\)) и регрессию “лассо” (при \(\lambda_1 = 0\)): \[ \hat{\beta} = \arg \min \left(\sum_{i=1}^n (y_i - \sum_{j=1}^m \beta_j x_{ij})^2 + \lambda_1 (\boldsymbol{\beta})^2 + \lambda_2 |\boldsymbol{\beta}|\right) \]
Продолжим рассмотрение примеров построения регрессионных моделей, прогнозирующих обилие водорослей группы a1 в зависимости от гидрохимических показателей воды и условий отбора проб в различных водотоках (см. подробное описание таблицы переменных в разделе 3.4):
Поскольку даже ориентировочная величина параметра регуляризации нам неизвестна, то на первом этапе с использованием функции glmnet() из одноименного пакета проведем анализ изменения значений коэффициентов в зависимости от \(\lambda\) в ее широком диапазоне от 0.1 до 1000 (рис. 4.4):
load(file = "algae.RData") # Загрузка таблицы algae - раздел 4.1grid = 10^seq(10, -2, length = 100)
library(glmnet)
lasso.a1 <- glmnet(x, algae$a1, alpha = 1, lambda = grid)
plot(lasso.a1, xvar = "lambda", label = TRUE, lwd = 2)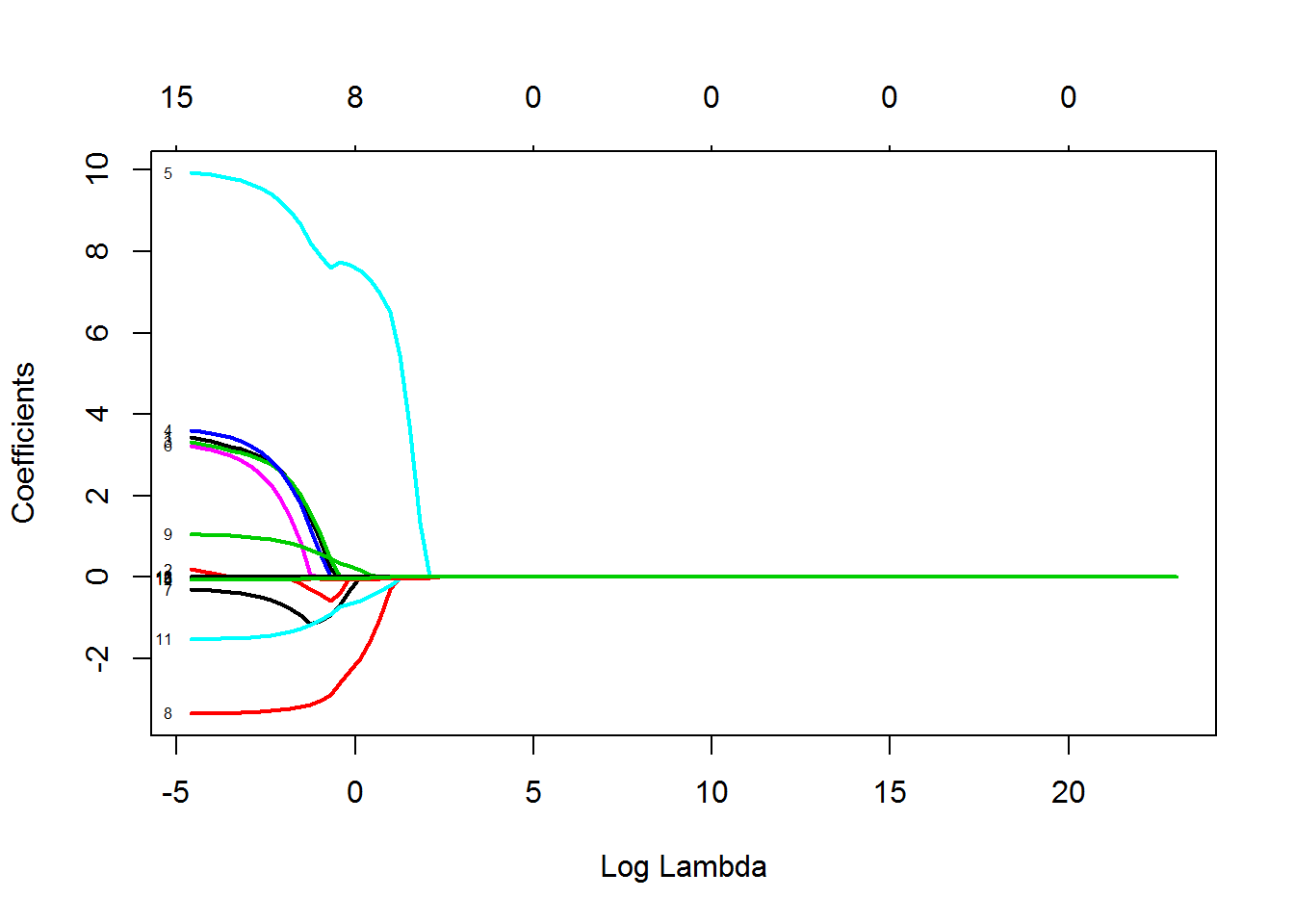
Рисунок 4.4: Зависимость коэффициентов регрессионной модели от значения параметра регуляризации
Функция train() для метода glmnet выполняет оптимизацию для двух моделей регуляризации: при alpha = 1 подгоняется модель по методу лассо, а при alpha = 0 - гребневая регрессия. Примем лассо-модель, и выполним тонкую настройку значения lambda в интервале от 0.5 до 4.5:
x <- model.matrix(a1 ~ ., data = algae[, 1:12])[, -1]
grid.train = seq(0.5, 4.5, length = 15)
lasso.a1.train <- train(as.data.frame(x), algae$a1,
method = 'glmnet',
tuneGrid = expand.grid(.lambda = grid.train, .alpha = 1),
trControl = trainControl(method = "cv"))Выведем протокол со значениями коэффициентов модели:
coef(lasso.a1.train$finalModel, lasso.a1.train$bestTune$lambda)## 16 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 36.14679706
## seasonspring .
## seasonsummer .
## seasonwinter .
## sizemedium .
## sizesmall 7.23680087
## speedlow .
## speedmedium .
## mxPH -1.43433769
## mnO2 0.01855714
## Cl -0.03931152
## NO3 -0.43978837
## NH4 .
## oPO4 .
## PO4 -0.05147194
## Chla -0.02086188Коэффициенты регрессии, отличные от 0, составляют информативный набор предикторов.
4.2.2 Метод частных наименьших квадратов (PLS)
В разделе 3.3 мы показали, как c помощью функции preProcess() можно на основе исходных переменных сформировать новое пространство главных компонент и построить модель классификации, прогнозирующую уровень доверия банка к клиенту. Напомним основные шаги построения модели регрессии на главные компоненты (PCR):
- стандартизация матрицы исходных предикторов \(\mathbf{X}\) и отклика \(\mathbf{Y}\);
- выбор числа собственных значений \(p\) и формирование матрицы главных компонент (часто называемой таблицей счетов - scores): \(\mathbf{T}_{n \times r} = \mathbf{X}_{n \times m} \mathbf{P}^T_{m \times p}\), где \(\mathbf{P}\) - матрица нагрузок (loadings);
- оценка вектора коэффициентов \(\mathbf{A}\) множественной регрессии на главные компоненты: \(\mathbf{Y = TA}\), \(\mathbf{A_r = (T^TT)^{-1}T^TY}\);
- пересчет коэффициентов регрессии на главные компоненты обратно в коэффициенты регрессии для исходных предикторов: \(\mathbf{B_m = PA}\).
Однако такой двухступенчатый подход (сжатие информативного пространства и последующая регрессия) - не самый обоснованный способ построения предсказательных моделей, поскольку PCA-преобразование данных далеко не всегда приводит к новым предикторам, наилучшим образом объясняющим отклик.
Метод частных наименьших квадратов PLS (Partial Least Squares, или Projection into Latent Structure) также использует разложение исходных предикторов по осям главных компонент, но дополнительно выделяет подмножество латентных переменных, в пространстве которых связь между зависимой переменной и предикторами достигает максимального значения.
В случае одномерного отклика сначала оценивается корреляционная связь между предикторами \(\mathbf{X}\) и \(\mathbf{Y}\), осуществляется сингулярное разложение матрицы \(\mathbf{X^TY}\), и формируется вектор \(\mathbf{W}\) первого направления PLS (direction), при вычислении которого особое внимание уделяется переменным, которые наиболее тесно связаны с откликом. Исходные переменные \(\mathbf{X}\) ортогонально проецируются на ось, задаваемую вектором \(\mathbf{W}\), а затем последовательно рассчитываются значения \(\mathbf{T}\) счетов и нагрузок \(\mathbf{P}\).
Для нахождения второго направления PLS вычисляются остатки, которые остались необъясненными первым PLS-направлением. Оценивается направление новой оси наибольшей корреляции и оцениваются значения счетов с использованием ортогонализированных остатков. Такой итеративный подход можно применить p раз пока модель не достигнет оптимальной сложности.
Реализация PLS-регрессии в среде R представлена в пакете pls, который включает в себя большое количество функций для построения регрессионных моделей, создания диагностических графиков и извлечения информации из результатов вычислений:
library(pls)
M.pls <- plsr(algae$a1 ~ x, scale = TRUE,
validation = "CV", method = "oscorespls")
summary(M.pls)## Data: X dimension: 200 15
## Y dimension: 200 1
## Fit method: oscorespls
## Number of components considered: 15
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 21.4 18.11 18.68 19.24 19.32 19.43 19.37
## adjCV 21.4 18.07 18.59 19.08 19.16 19.26 19.21
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 19.27 19.24 19.21 19.22 19.24 19.24 19.24
## adjCV 19.12 19.09 19.06 19.07 19.08 19.09 19.09
## 14 comps 15 comps
## CV 19.24 19.24
## adjCV 19.09 19.09
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
## X 22.08 30.32 36.14 43.04 50.35 59.24 66.02
## algae$a1 33.31 34.92 36.12 36.61 36.72 36.75 36.78
## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## X 71.89 77.01 80.97 87.28 90.78 94.76
## algae$a1 36.82 36.84 36.84 36.85 36.85 36.85
## 14 comps 15 comps
## X 98.08 100.00
## algae$a1 36.85 36.85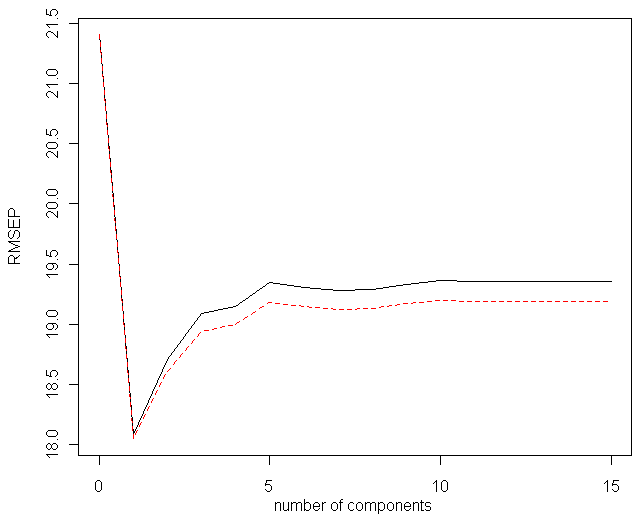
Рисунок 4.5: Зависимость ошибки перекрестной проверки от числа направлений PLS
Оптимальная модель основывается только на 1-м направлении PLS, поскольку при включении новых осей проецирования ошибка перекрестной проверки монотонно возрастает – см. рис. 4.5. Заметим, что накопленная доля объясненной дисперсии для матрицы предикторов X равномерно возрастает при увеличении числа компонент, тогда как почти вся вариация отклика algae$a1 сконцентрирована вдоль главного направления. Выполним подбор размерности пространства латентных переменных с использованием функции train(). По умолчанию диапазон значений оптимизируемого параметра ncomp принимает значения от 1 до tuneLength:
set.seed(100)
ctrl <- trainControl(method = "cv", number = 10)
(plsTune.a1 <- train(x, algae$a1, method = "pls",
tuneLength = 14, trControl = ctrl,
preProc = c("center", "scale")))## Partial Least Squares
##
## 200 samples
## 15 predictor
##
## Pre-processing: centered (15), scaled (15)
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 180, 180, 181, 180, 180, 180, ...
## Resampling results across tuning parameters:
##
## ncomp RMSE Rsquared
## 1 17.65378 0.3446070
## 2 18.19030 0.3059862
## 3 18.53369 0.2978422
## 4 18.57141 0.3000394
## 5 18.61605 0.3073643
## 6 18.60872 0.3096398
## 7 18.56721 0.3104612
## 8 18.54653 0.3094377
## 9 18.58432 0.3059038
## 10 18.58669 0.3053606
## 11 18.58870 0.3056950
## 12 18.58909 0.3055739
## 13 18.59139 0.3053874
## 14 18.59129 0.3054032
##
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was ncomp = 1.Выполним для сравнения подбор числа компонент для модели регрессии на главные компоненты PCR:
set.seed(100)
ctrl <- trainControl(method = "cv", number = 10)
(pcrTune.a1 <- train(x, algae$a1, method = "pcr",
tuneLength = 14, trControl = ctrl,
preProc = c("center", "scale")))## Principal Component Analysis
##
## 200 samples
## 15 predictor
##
## Pre-processing: centered (15), scaled (15)
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 180, 180, 181, 180, 180, 180, ...
## Resampling results across tuning parameters:
##
## ncomp RMSE Rsquared
## 1 17.55871 0.3516925
## 2 17.56938 0.3486775
## 3 17.68983 0.3462194
## 4 17.70050 0.3450229
## 5 17.73714 0.3419265
## 6 17.78112 0.3370401
## 7 17.73288 0.3335615
## 8 17.72616 0.3328631
## 9 17.88532 0.3211450
## 10 17.90557 0.3152904
## 11 17.93515 0.3125299
## 12 18.42456 0.2959252
## 13 18.52352 0.2949321
## 14 18.51619 0.3145490
##
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was ncomp = 1.Никаких преимуществ метода PLS по сравнению с PCR на нашем примере обнаружено не было; более того, в целом ошибка модели на главные компоненты оказалась несколько ниже.
4.2.3 Регрессия по методу k ближайших соседей
Ключевая идея, лежащая в основе метода \(k\) ближайших соседей, как уже обсуждалось в разделе 3.4, состоит в формулировке модели в терминах евклидовых расстояний в исходном многомерном пространстве признаков. Задача заключается в том, чтобы для каждой тестируемой точки \(\boldsymbol{x}_0\) найти такую \(\delta\)-окрестность (многомерный эллипсоид), чтобы в ней поместилось \(k\) точек с известными значениями \(y\). Тогда прогноз \(f(\boldsymbol{x}_0)\) можно получить, усредняя значения отклика всех обучающих наблюдений из \(\delta\).
Функция train() оптимизирует число соседей \(k\), используя другую функцию - knnreg() из пакета caret (рис. 4.6):5
knnTune.a1 <- train(x, algae$a1, method = "knn",
preProc = c("center", "scale"),
trControl = ctrl, tuneGrid = data.frame(.k = 4:25))
plot(knnTune.a1)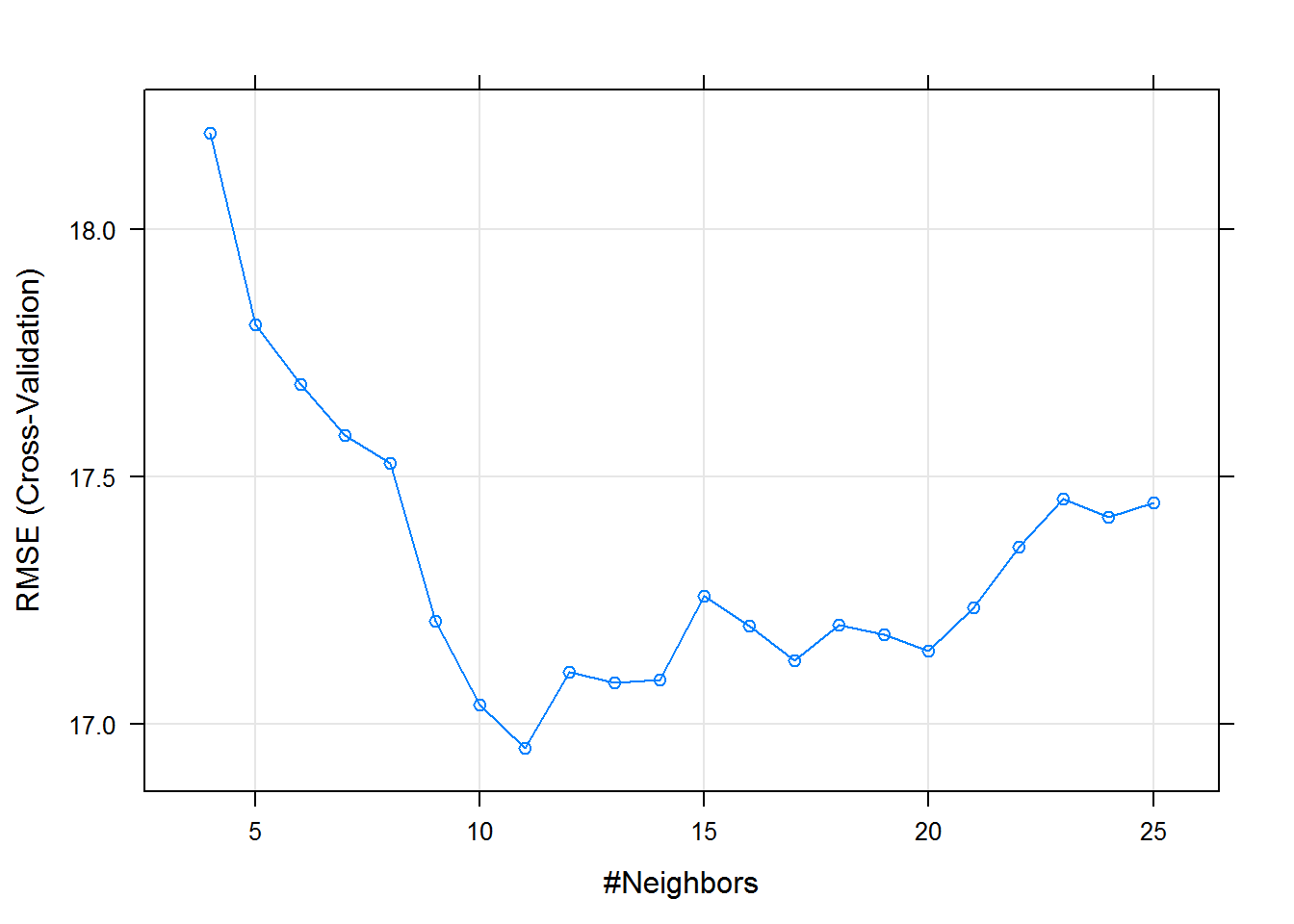
Рисунок 4.6: Зависимость ошибки перекрестной проверки от числа ближайших соседей
4.2.4 Тестирование моделей с использованием дополнительного набора данных
Используем для прогноза набор данных (Torgo, 2011) из 140 наблюдений, который мы уже применяли в предыдущем разделе. Данные, подготовленные для тестирования с восстановленными пропущенными значениями - таблицы Eval с предикторами и Sols со значениями отклика - мы сохранили в файле algae_test.RData (см раздел 4.1).
Выполним прогноз для набора предикторов проверочной выборки и оценим точность каждой модели по трем показателям: среднему абсолютному отклонению (MAE), корню из среднеквадратичного отклонения (RSME) и квадрату коэффициента детерминации Rsq = 1 - NSME, где NSME - относительная ошибка, равная отношению среднего квадрата отклонений от модельных значений и от общего среднего:
load(file="algae_test.RData") # Загрузка таблиц Eval, Solsy <- Sols$a1
EvalF <- as.data.frame(model.matrix(y ~ .,Eval)[,-1])
# Функция, выводящая вектор критериев
ModCrit <- function(pred, fact) {
mae <- mean(abs(pred - fact))
rmse <- sqrt(mean((pred - fact)^2))
Rsq <- 1 - sum((fact - pred)^2)/sum((mean(fact) - fact)^2)
c(MAE = mae, RSME = rmse, Rsq = Rsq ) }
Result <- rbind(
lasso = ModCrit(predict(lasso.a1.train, EvalF), Sols[, 1]),
pls_1c = ModCrit(predict(plsTune.a1, EvalF), Sols[, 1]),
pcr_1c = ModCrit(predict(pcrTune.a1, EvalF), Sols[, 1]),
kNN_21 = ModCrit(predict(knnTune.a1, EvalF), Sols[, 1]))
Result## MAE RSME Rsq
## lasso 12.80771 17.22026 0.2935004
## pls_1c 12.77453 17.28826 0.2879094
## pcr_1c 12.86125 17.30872 0.2862231
## kNN_21 12.22621 16.72561 0.3335055Отметим, что регрессия на главные компоненты и PLS в условиях слабой мультиколлинеарности данных не приносит никаких ощутимых преимуществ по сравнению с классическими линейными моделями раздела 4.1. Модель по методу лассо, отлично зарекомендовавшая себя при перекрестной проверке, сработала хуже на свежих данных, что связано, видимо, с дрейфом параметра регуляризации \(\lambda\) от своего оптимального значения. И, наконец, пока лучшей из всех исследованных оказалась методически простейшая модель регрессии по 21 ближайшему соседу. В то же время эта непараметрическая модель имеет важнейший недостаток - она не предоставляет никакой информации для графической или содержательной интерпретации.
Полученные вами результаты могут отличаться от приведенных здесь в силу случайного характера подвыборок, формируемых в ходе перекрестной проверки.↩