2.6 Методы кластеризации
В разделах 2.4-2.5 мы рассмотрели две процедуры: необъясненная (непрямая) ординация наблюдений, при которой конфигурация точек определяется случайной вариацией данных и не связывается с какими-либо внешними причинами, и прямая ординация с использованием объясняющих переменных (в рассмотренном примере - способ изготовления стекла). Ранжирование, непрямая ординация и кластеризация представляют собой совокупность методов обучения без учителя, основанных, как правило, на анализе расстояний между всеми возможными парами объектов в пространстве наблюдаемых независимых признаков. Такой подход, основанный на минимально возможном искажении исходной взаимной упорядоченности точек, обеспечивает наглядное графическое представление геометрической метафоры исследуемых объектов.
Под кластеризацией (от англ. cluster - гроздь, скопление) понимается задача разбиения всей исходной совокупности элементов на отдельные группы однородных объектов, сходных между собой, но имеющих отчетливые отличия этих групп друг от друга. Пусть \(d(х_i, х_j)\) - некоторая мера близости между каждой парой классифицируемых объектов \(i\) и \(j\). В качестве таковой может использоваться любая полезная функция: евклидово или манхэттенское расстояние, коэффициент корреляции Пирсона, расстояние \(\chi^2\), коэффициенты сходства Жаккара, Съеренсена, Ренконена и многие другие.
Наиболее часто применяется агломеративный иерархический алгоритм “дендрограмма”, отдельные версии которого отличаются правилами вычисления расстояния между кластерами. Дендрограммы просты в интерпретации и предоставляют полную информацию о соподчиненности всех классифицируемых объектов. Иногда они просто встраиваются в другие, более общие графики (например, “тепловые карты”), расширяя их понимание и возможность интерпретации.
Рассмотрим в качестве примера набор данных USArrests о криминогенной обстановке по штатам США (из пакета cluster). С помощью тепловой карты, представленной на рис. рис. 2.12, можно: а) разбить 50 штатов США на группы по криминальной напряженности, б) установить характер взаимосвязи между числом арестованных за убийство (Murder), изнасилование (Rape), разбой (Assault), а также долей городских жителей (UrbanPop) и, наконец, в) убедиться в том, что число изнасилований в Аляске много меньше, чем в Род-Айленде.
library(cluster)
data("USArrests")
x = as.matrix(USArrests)
rc <- rainbow(nrow(x), start = 0, end = .3)
cc <- rainbow(ncol(x), start = 0, end = .3)
hv <- heatmap(x, scale = "col", RowSideColors = rc,
ColSideColors = cc, margins = c(10,10),
cexCol = 1.5, cexRow = 1)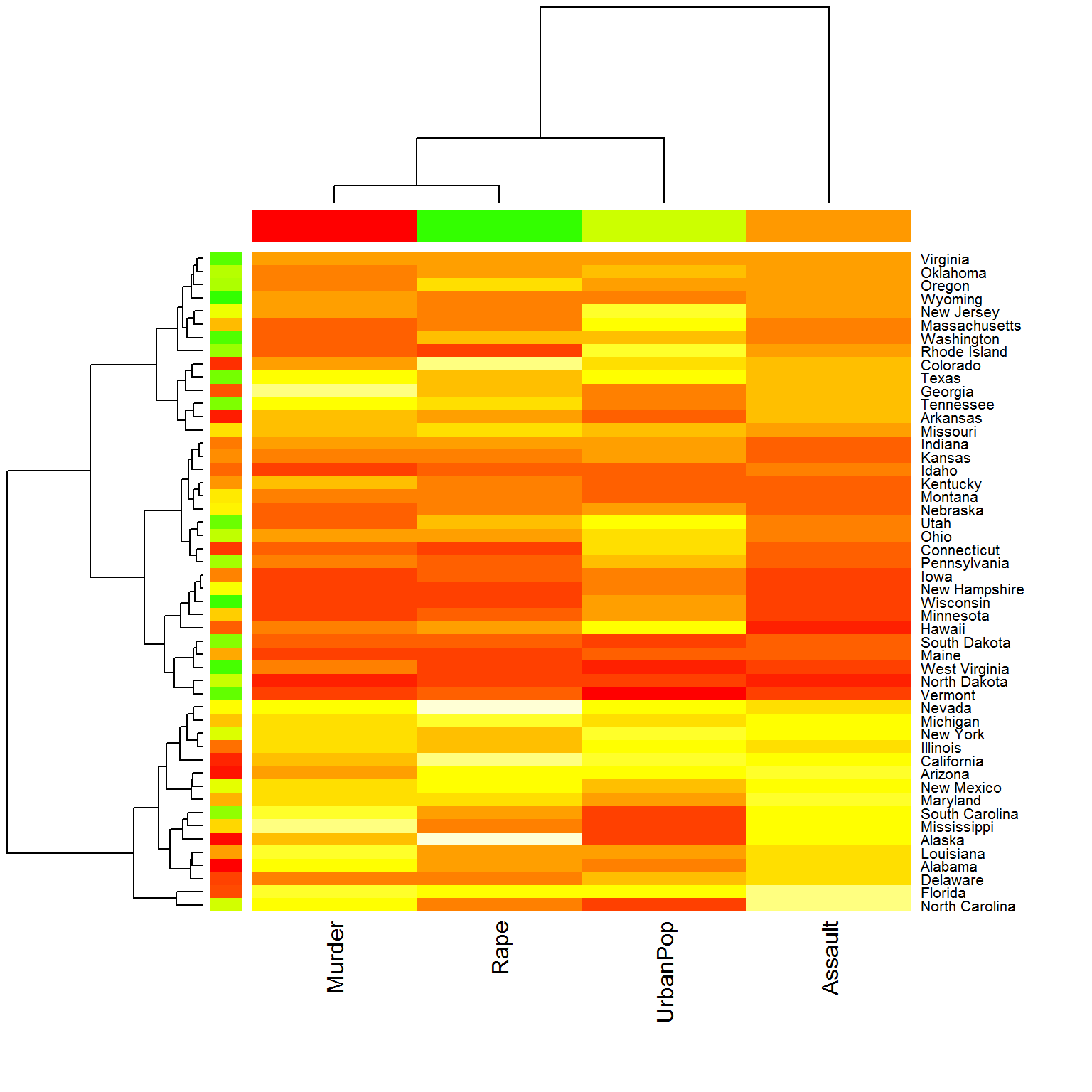
Рисунок 2.12: Пример тепловой карты с дендрограммами
Однако существенным недостатком иерархических методов является их детерминированность: объединение классов на более высоком уровне полностью определяется результатами агломерации на нижних уровнях. Для оценки того, какой из вариантов кластеризации в наибольшей степени отражает близость объектов в исходном признаковом пространстве, могут быть использованы кофенетическая корреляция (cophenetic correlation) или различные ранговые индексы.
Кроме иерархических методов классификации большое распространение также получили различные итерационные процедуры, которые пытаются найти наилучшее разбиение, ориентируясь на заданный критерий оптимизации, не строя при этом полного дерева. Наиболее популярный неиерархический алгоритм - метод \(k\) средних Мак-Кина, в котором сам пользователь должен задать искомое число конечных кластеров, обозначаемое как “\(k\)”. Его главным преимуществом является возможность обрабатывать очень большие массивы данных, поскольку нет необходимости хранить в памяти компьютера всю матрицу расстояний целиком.
Выполним разбиение 50 штатов на 5 классов по степени их криминализации:
df.stand <- as.data.frame(scale(USArrests))
(clus <- kmeans(df.stand, centers = 5))## K-means clustering with 5 clusters of sizes 5, 8, 13, 15, 9
##
## Cluster means:
## Murder Assault UrbanPop Rape
## 1 -1.1176648 -1.2258563 -1.6124616 -1.23334676
## 2 1.4118898 0.8743346 -0.8145211 0.01927104
## 3 0.6950701 1.0394414 0.7226370 1.27693964
## 4 -0.5069441 -0.4002992 0.6397341 -0.23901076
## 5 -0.7931716 -0.9304050 -0.4902018 -0.77805428
##
## Clustering vector:
## Alabama Alaska Arizona Arkansas California
## 2 3 3 2 3
## Colorado Connecticut Delaware Florida Georgia
## 3 4 4 3 2
## Hawaii Idaho Illinois Indiana Iowa
## 4 5 3 4 5
## Kansas Kentucky Louisiana Maine Maryland
## 4 5 2 1 3
## Massachusetts Michigan Minnesota Mississippi Missouri
## 4 3 5 2 3
## Montana Nebraska Nevada New Hampshire New Jersey
## 5 5 3 5 4
## New Mexico New York North Carolina North Dakota Ohio
## 3 3 2 1 4
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 4 4 4 4 2
## South Dakota Tennessee Texas Utah Vermont
## 1 2 3 4 1
## Virginia Washington West Virginia Wisconsin Wyoming
## 4 4 1 5 5
##
## Within cluster sum of squares by cluster:
## [1] 2.196512 8.316061 19.922437 14.960324 6.234959
## (between_SS / total_SS = 73.7 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss"
## [5] "tot.withinss" "betweenss" "size" "iter"
## [9] "ifault"Мы видим, что к каждому из пяти кластеров относится от 7 до 13 штатов, причем наибольший криминальный риск имеет место в 3 и 4 группах.
Любой алгоритм кластеризации может считаться результативным, если выполняется гипотеза компактности, т.е. можно найти такое разбиение объектов на группы, что расстояния между объектами из одной группы (intra-cluster distances) будут меньше некоторого значения \(\epsilon > 0\), а между объектами из разных групп (cross-cluster distance) - больше \(\epsilon\). Можно сформировать таблицу всех этих расстояний как показано ниже:
library('reshape2')
n <- dim(df.stand)[[1]]
euc.dist <- as.matrix(dist(df.stand))
dist = melt(euc.dist)
df.stand$cluster <- clus$cluster
pairs <- data.frame(dist = dist,
ca = as.vector(outer(1:n, 1:n,
function(a, b) df.stand[a, 'cluster'])),
cb = as.vector(outer(1:n, 1:n,
function(a, b) df.stand[b, 'cluster'])))
dcast(pairs, ca ~ cb, value.var = 'dist.value', mean)## ca 1 2 3 4 5
## 1 1 0.8192236 3.740748 4.651124 2.865534 1.589380
## 2 2 3.7407483 1.283606 2.556633 2.986930 3.136207
## 3 3 4.6511236 2.556633 1.584229 2.777835 3.656428
## 4 4 2.8655340 2.986930 2.777835 1.293573 1.822823
## 5 5 1.5893797 3.136207 3.656428 1.822823 1.030227В полученной таблице по главной диагонали приведены средние внутрикластерные расстояния, которые очевидно меньше, чем межкластерные расстояния (недиагональные элементы таблицы).
Поскольку объекты таблицы USArrests многомерны, то для вывода ординационной диаграммы выполним свертку информации по 4 имеющимся показателям к двум главным компонентам. После этого можно осуществить визуализацию групп (см. рис. 2.13) и “на глаз” оценить качество кластеризации.
c.pca <- prcomp(USArrests, center = TRUE, scale = TRUE)
d <- data.frame(x=c.pca$x[, 1], y=c.pca$x[, 2])
d$cluster <- clus$cluster
library('ggplot2')
library('grDevices')
h <- do.call(rbind, lapply(unique(clus$cluster),
function(c) { f <- subset(d,cluster==c); f[chull(f),]}))
ggplot() + geom_text(data = d,
aes(label = cluster, x = x, y = y, color = cluster),
size = 3) +
geom_polygon(data = h,
aes(x = x, y = y, group = cluster, fill = as.factor(cluster)),
alpha = 0.4, linetype = 0) +
theme(legend.position = "none")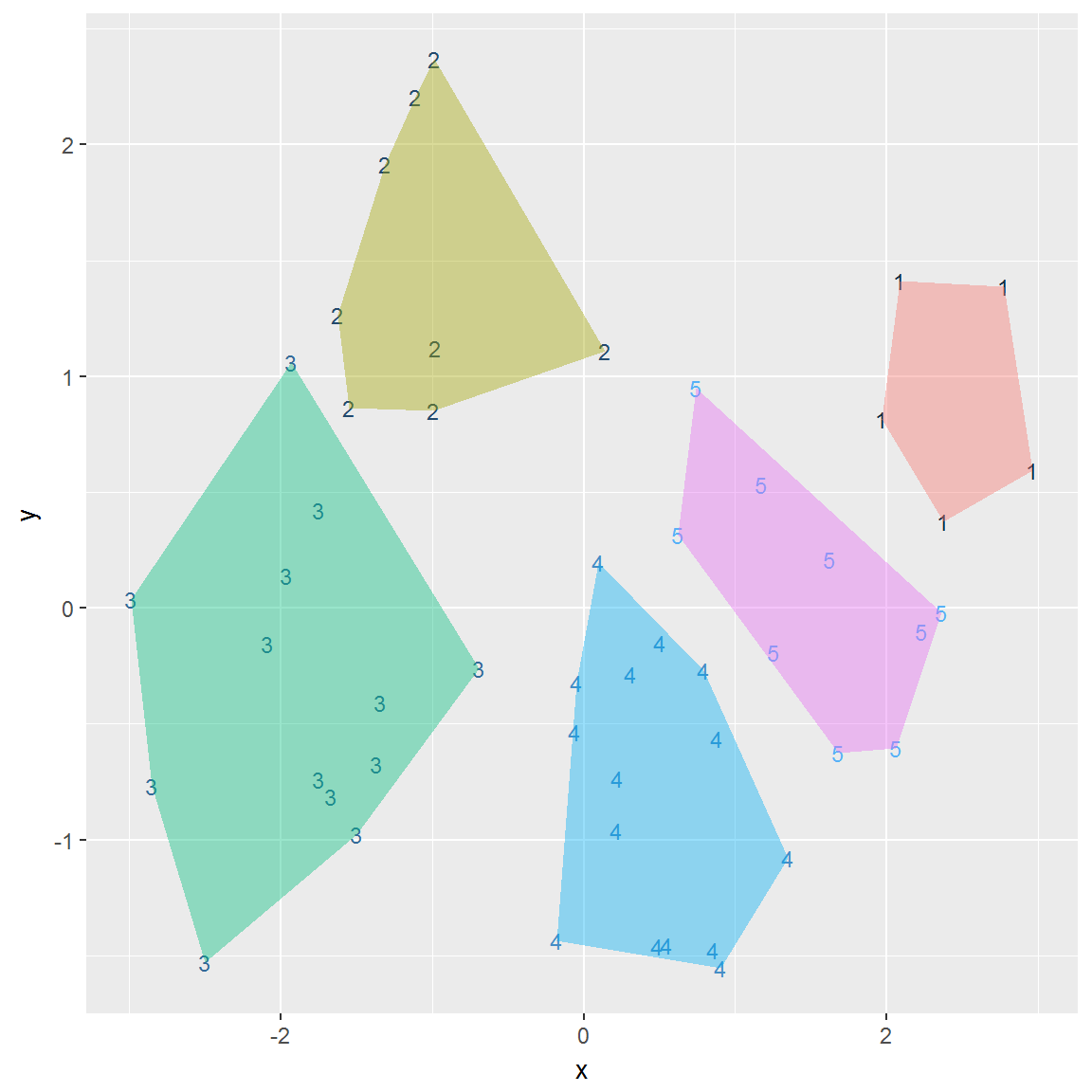
Рисунок 2.13: Пример кластеризации методом k средних
Другим современным подходом к кластеризации объектов являются алгоритмы типа нечетких C-средних и Гюстафсона-Кесселя (Барсегян и др., 2004), которые ищут кластеры в пространстве нечетких множеств в форме эллипсоидов, что делает эти методы более гибкими при решении различных практических задач. В литературе также описывается множество других методов кластеризации, не использующих матрицы сходств и основанных на оценивании функций плотности статистического распределения, эвристических алгоритмах перебора, идеях математического программирования. Каждый из них имеет специфическую идеологическую основу и подходы к построению критериев качества моделей, которые мы рассмотрим далее в главе 10.