8.2 Настройка параметров нейронных сетей средствами пакета caret
В разделе 7.5 мы рассмотрели основные принципы построения искусственных нейронных сетей на примере многослойного персептрона. Основная проблема обучения ИНС заключается в необходимости предварительно исследовать поверхность ошибок и задать архитектуру сети и параметры оптимизации, по возможности, приводящие в окрестность глобального минимума. С использованием функции train() из пакета caret путем перекрестной проверки можно оценить оптимальные значения числа скрытых нейронов size и параметр “ослабления весов” decay, который осуществляет регуляризацию точности подстройки коэффициентов (при decay = 0 стремление к точности может перерасти в эффект переусложнения модели). Покажем, как это можно сделать, на примере оценки возрастной категории морских ушек:
library(nnet)
library(caret)
load(file = "data/abalone.RData")
set.seed(123)
train.aba <- train(Возраст ~ ., data = abalone[, c(3:8, 10)],
method = "nnet", trace = FALSE, linout = 1,
tuneGrid = expand.grid(.decay = c(0, 0.05, 0.2), .size = 4:9),
trControl = trainControl(method = "cv"))
train.aba## Neural Network
##
## 4177 samples
## 6 predictor
## 4 classes: 'Q1', 'Q2', 'Q3', 'Q4'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 3760, 3759, 3758, 3759, 3761, 3759, ...
## Resampling results across tuning parameters:
##
## decay size Accuracy Kappa
## 0.00 4 0.5904016 0.4479233
## 0.00 5 0.5932764 0.4519404
## 0.00 6 0.5913671 0.4492714
## 0.00 7 0.5947176 0.4538315
## 0.00 8 0.5942397 0.4535296
## 0.00 9 0.5973469 0.4577817
## 0.05 4 0.5872990 0.4434182
## 0.05 5 0.5923240 0.4504110
## 0.05 6 0.5904085 0.4479034
## 0.05 7 0.5911262 0.4487974
## 0.05 8 0.5904090 0.4480305
## 0.05 9 0.5908841 0.4485251
## 0.20 4 0.5892094 0.4460456
## 0.20 5 0.5889650 0.4457956
## 0.20 6 0.5889702 0.4456556
## 0.20 7 0.5911233 0.4487412
## 0.20 8 0.5887310 0.4452668
## 0.20 9 0.5887229 0.4454816
##
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were size = 9 and decay = 0.Мы выполнили 10-кратную перекрестную проверку 18 нейросетевых моделей с числом нейронов в скрытом слое от 4 до 9 и разных значениях “ослабления”. При найденных значениях size = 7 и decay = 0, приводящих к максимальной точности Accuracy, построим далее модель с помощью функции nnet(). Для визуализации сети (рис. 8.6) применим функцию из скрипта nnet_plot_update.r, которая имеет ряд полезных опций (можно скачать с https://www.r-bloggers.com).
source("scripts/nnet_plot_update.r")
nn.aba <- nnet(Возраст ~ ., data = abalone[, c(3:8, 10)],
decay = 0, size = 7, niter = 200, trace = FALSE)
plot.nnet(nn.aba)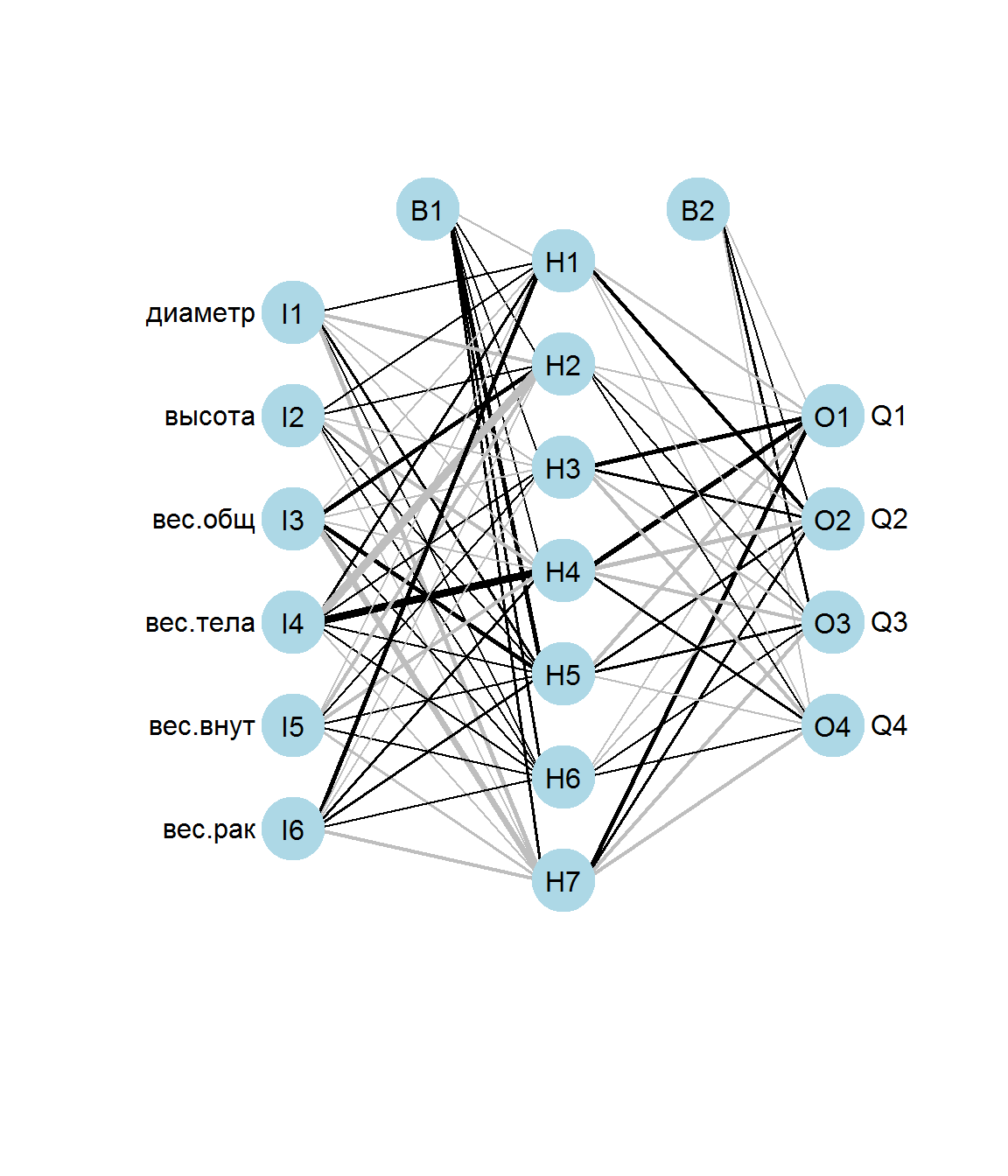
Рисунок 8.6: Персептрон для оценки возрастной категории морских ушек
Мы получили сеть из 17 нейронов (\(6 \Rightarrow 7 \Rightarrow 4\)), для которых рассчитано 81 нижеприведенных весовых коэффициентов и порогов b.
summary(nn.aba)## a 6-7-4 network with 81 weights
## options were - softmax modelling
## b->h1 i1->h1 i2->h1 i3->h1 i4->h1 i5->h1 i6->h1
## -0.34 2.99 0.43 -2.90 5.83 -4.60 19.04
## b->h2 i1->h2 i2->h2 i3->h2 i4->h2 i5->h2 i6->h2
## 4.63 -12.33 2.68 19.62 -40.48 -14.39 -0.02
## b->h3 i1->h3 i2->h3 i3->h3 i4->h3 i5->h3 i6->h3
## 1.52 -2.21 -3.20 -0.96 1.75 0.13 -3.35
## b->h4 i1->h4 i2->h4 i3->h4 i4->h4 i5->h4 i6->h4
## 1.88 -1.28 -12.34 -2.01 40.15 -14.49 7.50
## b->h5 i1->h5 i2->h5 i3->h5 i4->h5 i5->h5 i6->h5
## 19.41 9.95 3.98 16.32 4.67 4.44 5.46
## b->h6 i1->h6 i2->h6 i3->h6 i4->h6 i5->h6 i6->h6
## 5.65 1.83 0.96 1.18 1.31 0.13 0.41
## b->h7 i1->h7 i2->h7 i3->h7 i4->h7 i5->h7 i6->h7
## 5.72 -18.70 -4.43 -25.45 -0.72 -7.09 -11.77
## b->o1 h1->o1 h2->o1 h3->o1 h4->o1 h5->o1 h6->o1 h7->o1
## -3.54 -6.53 -2.53 16.48 20.87 -14.94 -2.48 16.14
## b->o2 h1->o2 h2->o2 h3->o2 h4->o2 h5->o2 h6->o2 h7->o2
## 0.48 10.76 -1.07 5.57 -16.73 6.81 -1.98 8.53
## b->o3 h1->o3 h2->o3 h3->o3 h4->o3 h5->o3 h6->o3 h7->o3
## 5.41 -2.51 0.93 -7.86 -11.87 7.88 3.52 -10.63
## b->o4 h1->o4 h2->o4 h3->o4 h4->o4 h5->o4 h6->o4 h7->o4
## -1.25 -3.73 4.25 -13.67 7.56 -0.76 0.63 -14.86Рассмотрим теперь, насколько хороша полученная нейросетевая модель при выполнении предсказаний:
pred <- predict(nn.aba, abalone[, 3:8], type = "class")
nn.table <- table(abalone[, 10], pred)
confusionMatrix(nn.table)## Confusion Matrix and Statistics
##
## pred
## Q1 Q2 Q3 Q4
## Q1 638 191 5 5
## Q2 160 777 246 74
## Q3 45 369 530 177
## Q4 11 156 262 531
##
## Overall Statistics
##
## Accuracy : 0.5928
## 95% CI : (0.5777, 0.6077)
## No Information Rate : 0.3574
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.4505
## Mcnemar's Test P-Value : < 2.2e-16
##
## Statistics by Class:
##
## Class: Q1 Class: Q2 Class: Q3 Class: Q4
## Sensitivity 0.7471 0.5204 0.5081 0.6747
## Specificity 0.9395 0.8212 0.8114 0.8735
## Pos Pred Value 0.7604 0.6181 0.4728 0.5531
## Neg Pred Value 0.9353 0.7548 0.8321 0.9204
## Prevalence 0.2045 0.3574 0.2497 0.1884
## Detection Rate 0.1527 0.1860 0.1269 0.1271
## Detection Prevalence 0.2009 0.3009 0.2684 0.2298
## Balanced Accuracy 0.8433 0.6708 0.6598 0.7741Точность предсказания возрастных категорий несколько возросла по сравнению с кумулятивным логитом (0.598 против 0.557), даже несмотря на то, что ковариату пол мы не использовали.
Рассмотрим кратко еще две функции из пакета caret, предназначенные для работы с искусственными нейронными сетями. Серьезной проблемой при обучении ИНС может стать высокая мультиколлинеарность предикторов. Одним из вариантов ее решения является проецирование исходной выборки в пространство главных компонент (см. метод PCR в разделе 4.2). Если задаться некоторым порогом (аргумент thresh), то значения \(p\) главных компонент, для которых накопленная доля объясненной дисперсии превышает этот порог, можно использовать как входы в нейронную сеть и настроить ее обычным способом как для регрессии, так и для классификации.
Функция pcaNNet() является своеобразной оберткой для совместного выполнения предобработки данных, анализа главных компонент, и запуска функции nnet() для обучения сети на полученных главных компонентах.
Выполним обучение сети для предсказания возрастной категории морских ушек с использованием параметра thresh = 0.975 и числа нейронов в скрытом слое size = 7:
pcaNNet.Fit <- pcaNNet(abalone[, 3:8], abalone[,10],
size = 7, thresh = 0.975,
linout = TRUE, trace = FALSE)При значении thresh = 0.975 на вход сети подается 4 главных компоненты, отвечающих этому условию. Для тестируемых данных такое же преобразование (основанное на факторных нагрузках для обучающего множества) применяется к новым значениям предикторов.
pred <- predict(pcaNNet.Fit, abalone[, 3:8], type = "class")
(table(Факт = abalone$Возраст, Прогноз = pred))## Прогноз
## Факт Q1 Q2 Q3 Q4
## Q1 639 186 6 8
## Q2 172 730 259 96
## Q3 51 324 521 225
## Q4 12 146 272 530Acc <- mean(pred == abalone$Возраст)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=57.94%"В разделе 4.4 была описана процедура бэггинга, как общего метода агрегирования моделей произвольной структуры, построенных на бутстреп-выборках из исходного набора данных. Функция avNNet() осуществляет обучение заданного множества моделей нейронной сети на одном и том же наборе данных. Модели могут различаться как из-за случайного дрейфа стартовых параметров калибровки сети (Ripley, 1996), так и вследствие использования бутстреп-выборок, извлеченных из исходного обучающего множества. Для моделей классификации функция avNNet() оценивает среднее значение вероятностей классов на основе частных прогнозов каждой из моделей созданного ансамбля и далее производит заключительное предсказание класса.
Для рассматриваемого примера сформируем 10 экземпляров моделей ИНС с использованием бэггинга:
avNNet.Fit <- avNNet(Возраст ~ ., data = abalone[, c(3:8, 10)],
size = 7, repeats = 10, linout = TRUE,
trace = FALSE, bag = TRUE)
pred <- predict(avNNet.Fit, abalone[, 3:8], type = "class")
Acc <- mean(pred == abalone$Возраст)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=59.11%"