Классификация, регрессия и другие алгоритмы Data Mining с использованием R

6.4 Деревья классификации, случайный лес и логистическая регрессия

Выполним построение еще трех бинарных классификаторов для предсказания марки стекла на основе методов, использованных нами в главе 4 при выполнении регрессионного анализа.

Как упоминалось ранее, деревья решений CART могут эффективно применяться и для прогнозирования бинарного отклика. При построении дерева важно установить оптимальный уровень ветвления и выбрать значение относительного параметра стоимости сложности cp. Визуализацию дерева выполним с помощью пакета rpart.plot (рис. 6.7):

DGlass <- read.table(file = "data/Glass.txt", sep = ",",
                     header = TRUE, row.names = 1)
DGlass$FAC <- as.factor(ifelse(DGlass$Class == 2, "No", "Flash"))
control <- trainControl(method = "repeatedcv", number = 10,repeats = 3)
set.seed(7)
fit.cart <- train(DGlass[, 1:9], DGlass$FAC, 
                  method = "rpart", trControl = control)
library(rpart.plot)
rpart.plot(fit.cart$finalModel)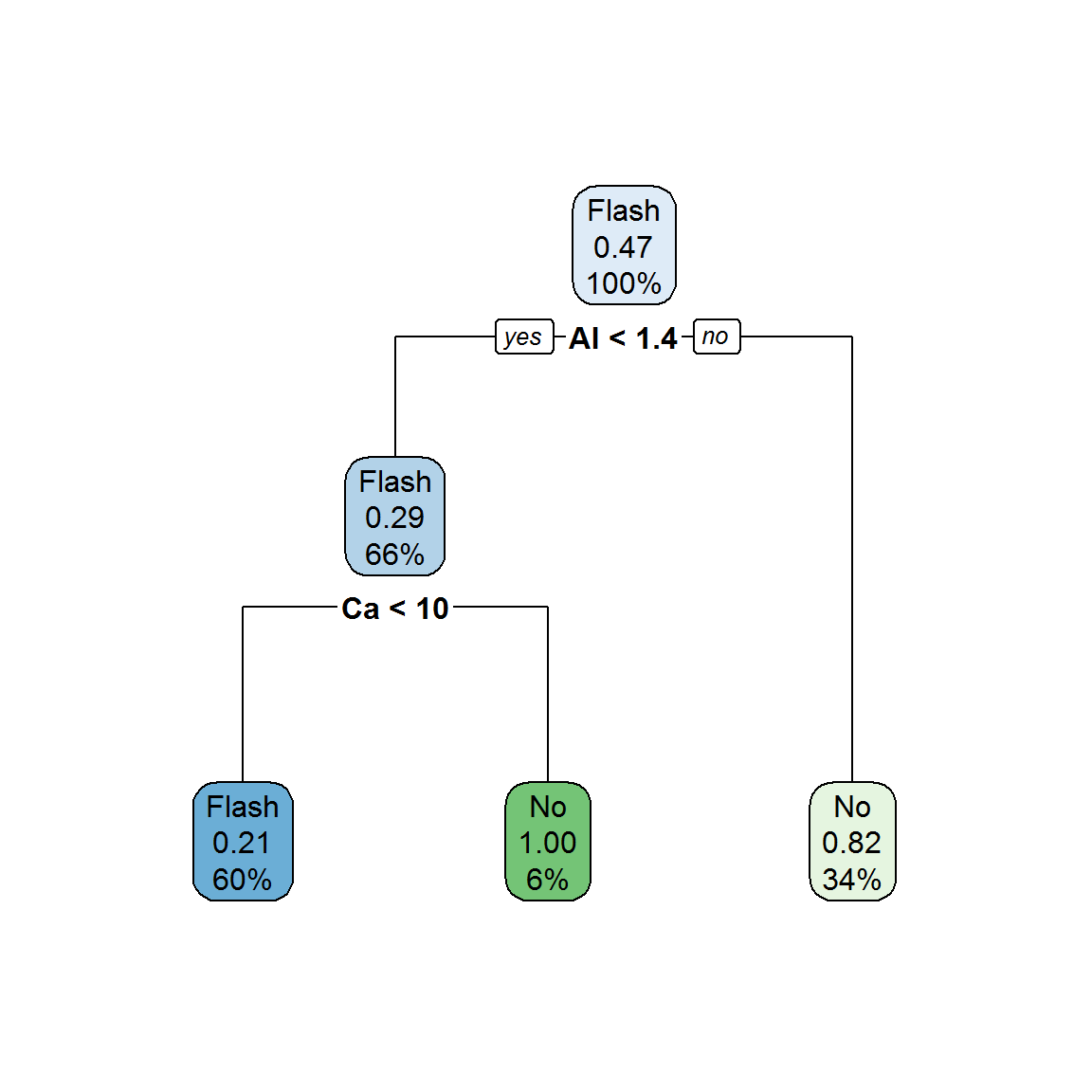

Рисунок 6.7: Дерево rpart для прогнозирования типа стекла

В узлах и листьях дерева на рис. 6.7 указаны доля примеров в этой группе от объема всей обучающей выборки (%) и вероятность прогноза “не флэш-стекло”. Оценим адекватность модели по точности прогноза на обучающей выборке:

pred <- predict( fit.cart, DGlass[, 1:9])
(table(Факт = DGlass$FAC, Прогноз = pred))

##        Прогноз
## Факт    Flash No
##   Flash    77 10
##   No       21 55

Acc <- mean(pred == DGlass$FAC)
paste("Точность=", round(100*Acc, 2), "%", sep = "")

## [1] "Точность=80.98%"

Метод случайного леса (random forest) осуществляет бутстреп-агрегирование некоторого множества деревьев решений. Для создания оптимального ансамбля необходимо выбрать значение mtry, определяющее число исходных переменных, которые участвуют в выращивании деревьев:

set.seed(7)
fit.rf <- train(DGlass[, 1:9], DGlass$FAC, 
                method = "rf", trControl = control)
fit.rf$finalModel

## 
## Call:
##  randomForest(x = x, y = y, mtry = param$mtry) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 2
## 
##         OOB estimate of  error rate: 12.88%
## Confusion matrix:
##       Flash No class.error
## Flash    81  6  0.06896552
## No       15 61  0.19736842

pred <- predict(fit.rf, DGlass[, 1:9])
(table(Факт = DGlass$FAC, Прогноз = pred))

##        Прогноз
## Факт    Flash No
##   Flash    87  0
##   No        0 76

Acc <- mean(pred == DGlass$FAC)
paste("Точность=", round(100*Acc, 2), "%", sep="")

## [1] "Точность=100%"

Из протокола расчетов видно, что: а) на каждом шаге ветвления выбор идет только из двух случайных переменных, б) в итоге был составлен ансамбль из 500 деревьев, в) средняя ошибка по наблюдениям, не попавшим в “сумку” (OOB error), равна 12.27%, г) модель правильно предсказывает класс всех объектов обучающей выборки.

Приступим теперь к построению логистической регрессии LR, как это было сделано в разделе 5.1:

DGlass$FAC <- ifelse(DGlass$Class == 2, 1, 0)
logit.all <- glm(FAC ~ ., data = DGlass[, -10], family = binomial)
mp.all <- predict(logit.all, type = "response")
Acc <- mean(DGlass$FAC == ifelse(mp.all > 0.5, 1, 0))
paste("Точность=", round(100*Acc, 2), "%", sep = "")

## [1] "Точность=73.62%"

Получим теперь ошибку перекрестной проверки по методу скользящего контроля с использованием функции cv.glm() из пакета boot. Обратим внимание на необходимость функции cost, которая пересчитывает значение delta из ошибки оценки вероятностей в ошибку предсказания класса:

library(boot)
cost <- function(r, pi = 0) mean(abs(r - pi) > 0.5)
Acc <- 1 - cv.glm(DGlass[,-10], logit.all, cost)$delta[1]
paste("Точность=", round(100*Acc, 2), "%", sep = "")

## [1] "Точность=68.71%"

Выполним пошаговую процедуру селекции независимых переменных и оценим ошибки предсказания:

# Регрессия на информативные переменные
logit.step <- step(logit.all, trace = 0)
summary(logit.step)

## 
## Call:
## glm(formula = FAC ~ RI + Na + Mg + Si + K + Ca + Ba, family = binomial, 
##     data = DGlass[, -10])
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.0742  -0.8878  -0.2400   0.8731   2.0119  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -328.3768   352.0813  -0.933 0.350989    
## RI           472.1567   235.8428   2.002 0.045285 *  
## Na            -3.6626     1.1071  -3.308 0.000939 ***
## Mg            -5.9264     1.1531  -5.140 2.75e-07 ***
## Si            -3.7897     0.9963  -3.804 0.000143 ***
## K             -3.1497     2.1582  -1.459 0.144455    
## Ca            -4.9433     1.1783  -4.195 2.73e-05 ***
## Ba            -5.6440     3.0682  -1.840 0.065838 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 225.22  on 162  degrees of freedom
## Residual deviance: 166.92  on 155  degrees of freedom
## AIC: 182.92
## 
## Number of Fisher Scoring iterations: 6

# Ошибка на обучающей выборке
mp.step <- predict(logit.step, type = "response")
Acc <- mean(DGlass$FAC == ifelse(mp.step > 0.5, 1, 0))
paste("Точность=", round(100*Acc, 2), "%", sep = "")

## [1] "Точность=71.78%"

# Ошибка при скользящем контроле
Acc <- 1 - cv.glm(DGlass[, -10], logit.step, cost)$delta[1]
paste("Точность=", round(100*Acc, 2), "%", sep = "")

## [1] "Точность=69.33%"

Исключение нескольких переменных не привело к улучшению характеристик модели логистической регрессии. Если использовать метод RFE, то можно прийти к тому же подмножеству предикторов, а тестирование моделей с применением функции train() приведет примерно к такому же соотношению эффективности обоих моделей (читатели могут проверить это самостоятельно).