ГЛАВА 7 Модели классификации для нескольких классов

7.1 Ирисы Фишера и метод k ближайших соседей

Ирисы Фишера - самый популярный в статистической литературе набор данных, часто используемый для иллюстрации работы различных алгоритмов классификации. При всем желании мы не смогли без него обойтись, поскольку в современных реальных приложениях редко встречаются такие компактные наборы данных, позволяющие построить хороший классификатор при минимуме исходных признаков.

Выборка состоит из 150 экземпляров ирисов трех видов (рис. 7.1), для которых измерялись четыре характеристики: длина и ширина чашелистика (Sepal.Length и Sepal.Width), длина и ширина лепестка (Petal.Length и Petal.Width). Поставим своей задачей на основе этого набора данных, включенного в базовый дистрибутив R, построить различные модели многоклассовой классификации, оценивающие каждый из трех видов растения по данным проведенных измерений.

Виды ирисов в выборке Фишера-Андерсона

Рисунок 7.1: Виды ирисов в выборке Фишера-Андерсона

Исследуем характер статистической вариации признаков этой выборки с использованием категоризованных диаграмм, где данные сгруппированы по отдельным видам. Из графиков, представленных на рис. 7.2, видно, что размеры лепестка Petal.Width являются гораздо более выраженным классифицирующим признаком, чем ширина чашелистика.

data(iris)
library(ggplot2)
library(gridExtra)
a <- qplot(Sepal.Length, Sepal.Width, data = iris) +
    facet_grid(facets = ~ Species) +
    geom_smooth(color = "red", se = FALSE) 
b <- qplot(Petal.Length, Petal.Width,data = iris) +
    facet_grid(facets = ~ Species) +
    geom_smooth(color = "red", se = FALSE)
grid.arrange(a, b, nrow = 2)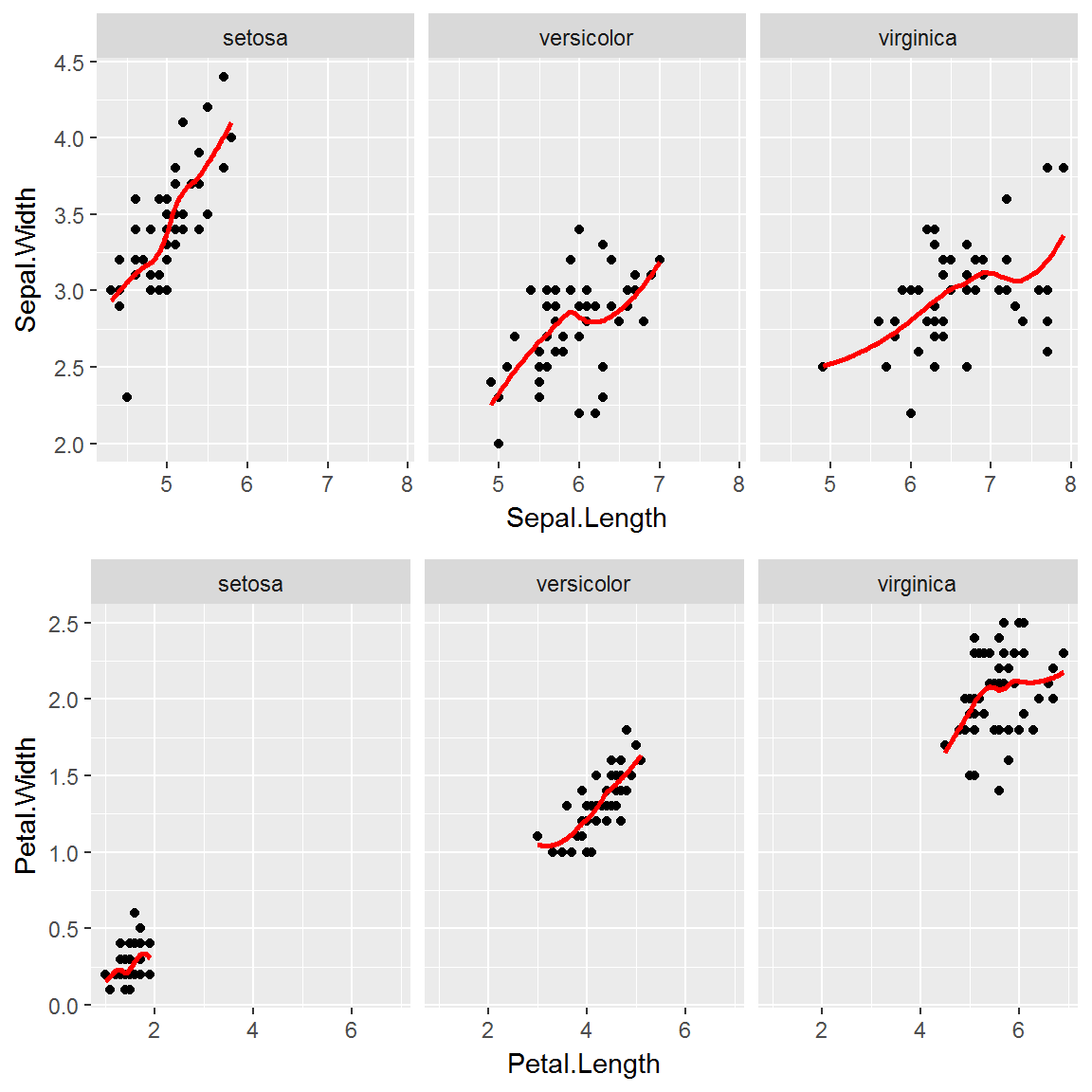
Категоризованная диаграмма выборки ирисов

Рисунок 7.2: Категоризованная диаграмма выборки ирисов

Выполним теперь визуализацию анализируемых данных в пространстве первых двух главных компонент (рис. 7.3):

library(vegan)
mod.pca <- vegan::rda(iris[, -5], scale = TRUE)
scores <- as.data.frame(vegan::scores(mod.pca, display = "sites",
                               scaling = 3))
scores$Species <- iris$Species
# Включаем в названия осей доли объясненных дисперсий
axX <- paste("PC1 (",
             as.integer(100*mod.pca$CA$eig[1]/sum(mod.pca$CA$eig)), "%)")
axY <- paste("PC2 (",
             as.integer(100*mod.pca$CA$eig[2]/sum(mod.pca$CA$eig)), "%)")
# Составляем таблицу для "каркаса" точек
l <- lapply(unique(scores$Species), function(c) { 
    f <- subset(scores, Species == c)
    f[chull(f), ]})
hull <- do.call(rbind, l)
# Выводим ординационную диаграмму
ggplot() + 
    geom_polygon(data = hull, aes(x = PC1, y = PC2, fill = Species),
                 alpha = 0.4, linetype = 0) +  
    geom_point(data = scores, aes(x = PC1, y = PC2, shape = Species,
                                  colour = Species), size = 3) + 
    scale_colour_manual(values = c('purple', 'green', 'blue')) +
    xlab(axX) + ylab(axY) + coord_equal() + theme_bw()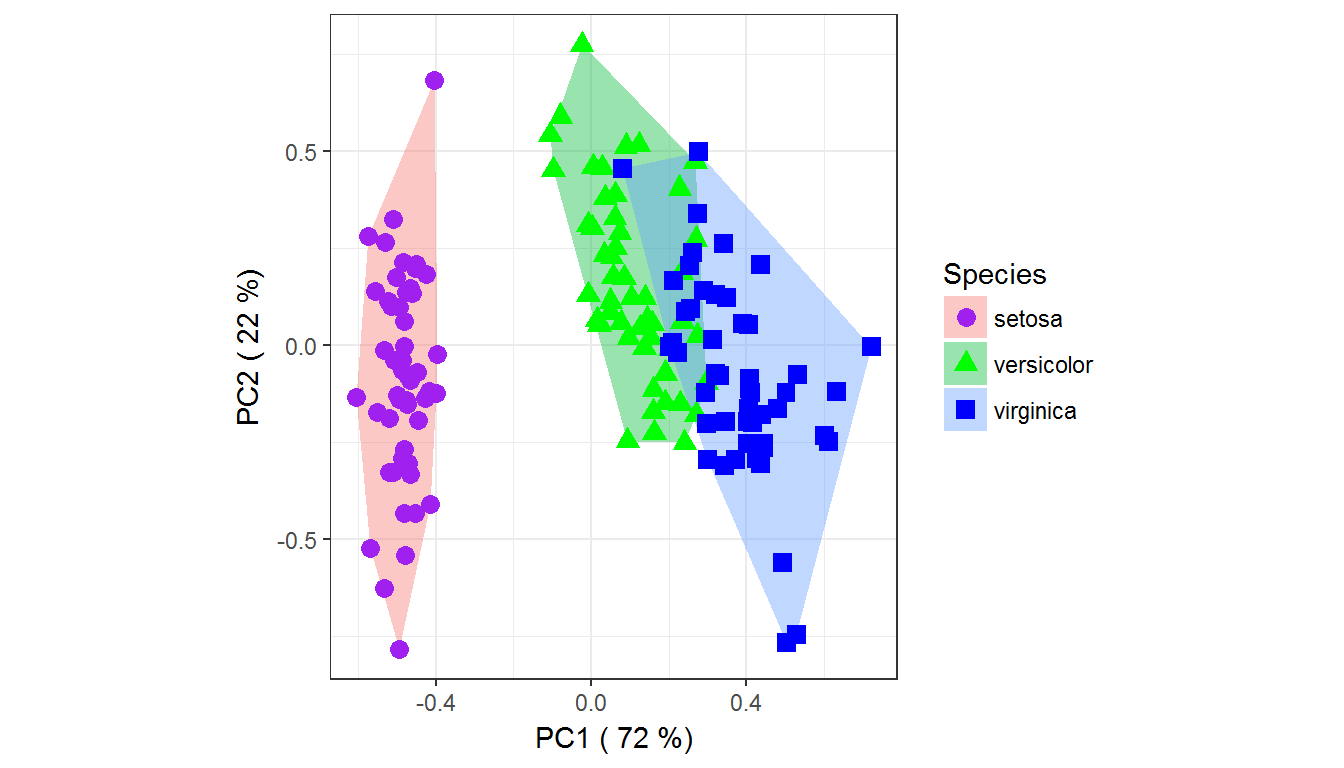
Ординационная диаграмма данных по ирисам в осях двух главных компонент

Рисунок 7.3: Ординационная диаграмма данных по ирисам в осях двух главных компонент

Как видно на рис. 7.3, один из классов (Iris setosa) линейно отделим от двух остальных.

В разделах 3.4 и 4.2 мы использовали простейший, но достаточно эффективный алгоритм \(k\) ближайших соседей (k nearest neighbors), или kNN-регрессию. В основе метода kNN-классификатора лежит гипотеза компактности, которая предполагает, что тестируемый объект d будет иметь такую же метку класса, как и обучающие объекты в локальной области его ближайшего окружения. В варианте 1NN анализируемый объект относят к определенному классу в зависимости от информации о его ближайшем соседе. В варианте kNN каждый объект относится к преобладающему классу ближайших соседей, где \(k\) - параметр алгоритма.

Решающие правила в методе kNN определяются границами смежных сегментов диаграммы Вороного (Voronoi resselation), разделяющей плоскость на \(n\) выпуклых многоугольников, каждый из которых содержит один и только один объект обучающей выборки (рис. 7.4). В \(p\)-мерных пространствах границы решений состоят уже из сегментов \((p - 1)\)-мерных полуплоскостей, образованных выпуклыми многогранниками Вороного.

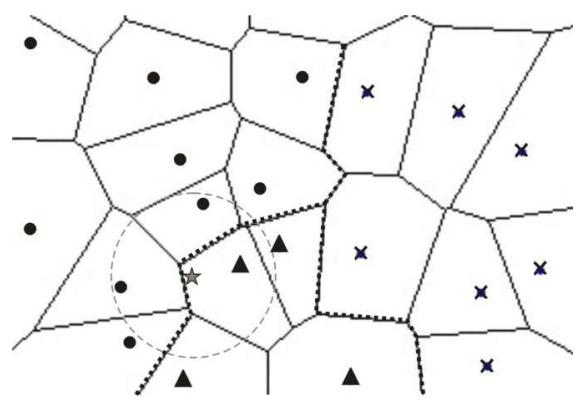
Иллюстрация работы алгоритма *k* ближайших соседей

Рисунок 7.4: Иллюстрация работы алгоритма k ближайших соседей

Алгоритм предсказания строится по принципу “большинства голосов”, т.е. в качестве результата объявляется метка класса-победителя. На рис. 7.4 тестируемый объект “звёздочка” попадает в ячейку объекта класса “треугольников” и при \(k = 1\) будет отнесён к этому классу. Однако при \(k = 3\) по голосам двух ближайших соседей из трех экзаменуемая точка будет отнесена к классу “кружочков”. Вероятностный вариант метода kNN использует для ранжирования предполагаемых классов сумму “голосов” соседей с учетом их весов, в частности, евклидовой меры расстояния между тестируемым объектом и каждым из соседей.

Вариант 1NN всегда обеспечивает 100% правильное распознавание примеров обучающей выборки (самый ближайший сосед - он сам), однако часто ошибается на неизвестных ему данных. При увеличении \(k > 1\) до некоторых пределов качество распознавания на контрольной выборке будет возрастать. Оптимальное в смысле точности предсказаний значение \(k\) может быть найдено с использованием перекрестной проверки. Для этого по фиксированному значению \(k\) строится модель \(k\)-ближайших соседей и оценивается CV-ошибка классификации. Эти действия повторяются для различных \(k\) и значение, соответствующее наименьшей ошибке распознавания, принимается как оптимальное.

В среде R классификация методом ближайших соседей может быть выполнена функциями knn() из базового пакета class и kknn() из одноименного пакета с расширенными возможностями настройки меры близости и формы используемой ядерной функции. Существует несколько возможностей оценить оптимальное значение k с помощью кросс-проверки:

  1. Воспользоваться функцией train.kknn() из пакета kknn (по умолчанию задается скользящий контроль):
library(kknn)
train.kknn(Species ~ ., iris, kmax = 50, kernel = "rectangular") 
## 
## Call:
## train.kknn(formula = Species ~ ., data = iris, kmax = 50, kernel = "rectangular")
## 
## Type of response variable: nominal
## Minimal misclassification: 0.02666667
## Best kernel: rectangular
## Best k: 16
  1. Составить собственный скрипт для выполнения перекрестной проверки, например (рис. 7.5):
max_K = 20
gen.err.kknn <- numeric(max_K)
mycv.err.kknn <- numeric(max_K)
n <- nrow(iris)

#  Рассматриваем число возможных соседей от 1 до 20
for (k.val in 1:max_K)  {  
    pred.train <- kknn(Species ~ ., iris,
                       train = iris, test = iris, k = k.val, 
                       kernel = "rectangular")
    gen.err.kknn[k.val] <- mean(pred.train$fit != iris$Species)
    for (i in 1:n)   {
        pred.mycv <- kknn(Species ~ ., train = iris[-i, ], test = iris[i, ],
                          k = k.val, kernel = "rectangular")
        mycv.err.kknn[k.val] <- mycv.err.kknn[k.val] +
            (pred.mycv$fit != iris$Species[i]) }
}
mycv.err.kknn <- mycv.err.kknn/n

plot(1:20, gen.err.kknn, type = "l", xlab = 'k', ylim = c(0, 0.07),
     ylab = 'Ошибка классификации', col = "limegreen", lwd = 2) 
points(1:max_K, mycv.err.kknn, type = "l", col = "red", lwd = 2)
legend("bottomright", c("При обучении", "Скользящий контроль"),
       lwd = 2, col = c("limegreen", "red"))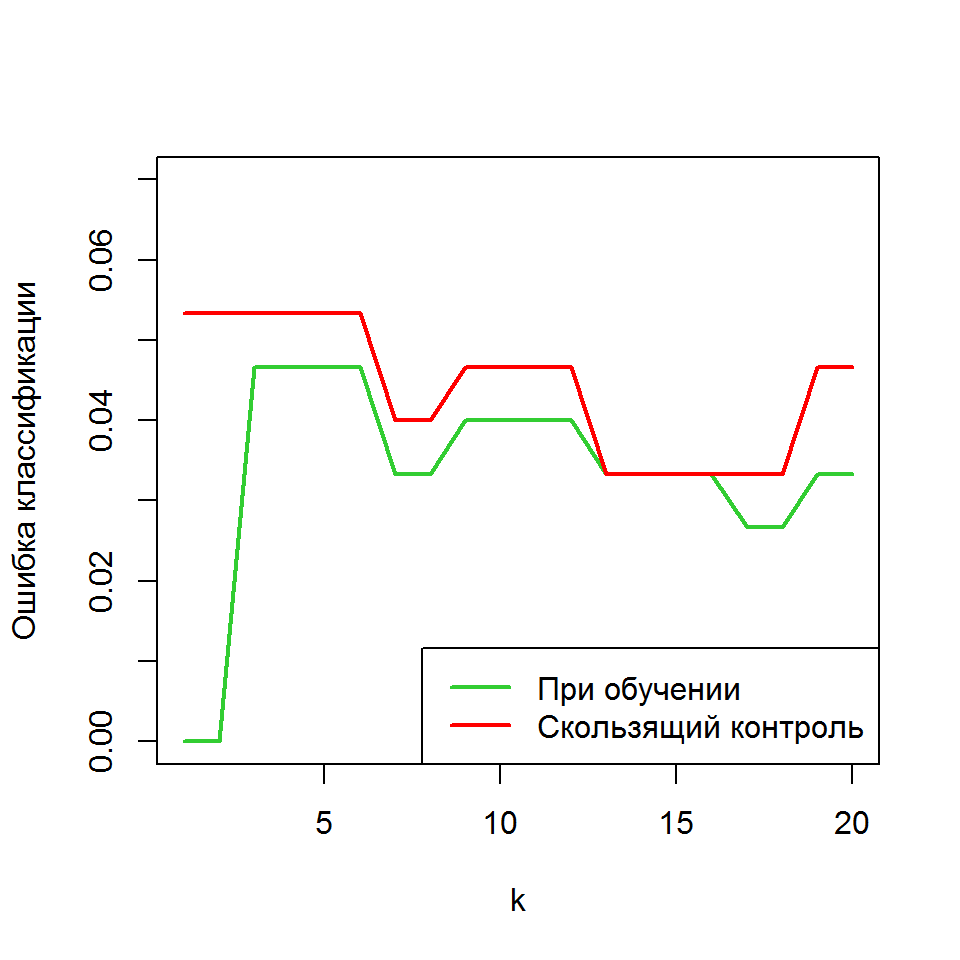
Нахождение оптимального числа $k$ ближайших соседей при классификации видов ириса

Рисунок 7.5: Нахождение оптимального числа \(k\) ближайших соседей при классификации видов ириса

  1. Использовать функцию train() из пакета caret, с которой мы уже неоднократно сталкивались ранее (см. главу 3):
library(caret)
set.seed(123)
contrl <- trainControl(method = "repeatedcv", repeats = 3)
train(Species ~ ., data = iris, method = "kknn", 
      trControl = contrl, preProcess = c("center", "scale"),
      tuneLength = 20)
## k-Nearest Neighbors 
## 
## 150 samples
##   4 predictor
##   3 classes: 'setosa', 'versicolor', 'virginica' 
## 
## Pre-processing: centered (4), scaled (4) 
## Resampling: Cross-Validated (10 fold, repeated 3 times) 
## Summary of sample sizes: 135, 135, 135, 135, 135, 135, ... 
## Resampling results across tuning parameters:
## 
##   kmax  Accuracy   Kappa    
##    5    0.9466667  0.9200000
##    7    0.9466667  0.9200000
##    9    0.9466667  0.9200000
##   11    0.9488889  0.9233333
##   13    0.9555556  0.9333333
##   15    0.9555556  0.9333333
##   17    0.9555556  0.9333333
##   19    0.9555556  0.9333333
##   21    0.9555556  0.9333333
##   23    0.9555556  0.9333333
##   25    0.9555556  0.9333333
##   27    0.9555556  0.9333333
##   29    0.9577778  0.9366667
##   31    0.9577778  0.9366667
##   33    0.9577778  0.9366667
##   35    0.9577778  0.9366667
##   37    0.9577778  0.9366667
##   39    0.9577778  0.9366667
##   41    0.9577778  0.9366667
##   43    0.9577778  0.9366667
## 
## Tuning parameter 'distance' was held constant at a value of 2
## 
## Tuning parameter 'kernel' was held constant at a value of optimal
## Accuracy was used to select the optimal model using  the largest value.
## The final values used for the model were kmax = 43, distance = 2
##  and kernel = optimal.

Здесь была осуществлена трехкратная перекрестная проверка с разбивкой на 10 блоков, т.е. случайным образом исходная выборка делилась на 10 частей, после чего поочередно 9 частей использовались для оценки \(k\), а по одной части оценивалась точность классификации, и такая процедура повторялась три раза.

Выполним теперь стандартную процедуру тестирования модели при \(k = 13\). Исходную выборку разбиваем на две части: обучающую (train) и проверочную (test) в соотношении 3:1:

set.seed(123)
(samp.size <- floor(nrow(iris) * .75))
## [1] 112
train.ind <- sample(seq_len(nrow(iris)), size = samp.size)
train <- iris[train.ind, ]
test <- iris[-train.ind, ]

Функция knn() из пакета class сразу на выходе дает предсказываемые значения для тестовой последовательности, которые можно использовать для построения матрицы неточностей:

knn.iris <- class::knn(train = train[, -5], test = test[, -5], 
                cl = train[, "Species"], k = 13, prob = TRUE)
(table(Факт = test$Species, Прогноз = knn.iris))
##             Прогноз
## Факт         setosa versicolor virginica
##   setosa         11          0         0
##   versicolor      0         13         0
##   virginica       0          1        13
Acc <- mean(knn.iris == test$Species)
paste("Точность=", round(100*Acc, 2), "%", sep = "")
## [1] "Точность=97.37%"

Метод дал одну ошибку при предсказании 38 “свежих” примеров, что является вполне приличным результатом.