Классификация, регрессия и другие алгоритмы Data Mining с использованием R

6.2 Метод опорных векторов

Метод опорных векторов (support vector), называемый ранее алгоритмом “обобщенного портрета”, был разработан советскими математиками В. Н. Вапником и А. Я. Червоненкисом (1974) и с тех пор приобрел широкую популярность.

Основная идея классификатора на опорных векторах заключается в том, чтобы строить разделяющую поверхность с использованием только небольшого подмножества точек, лежащих в зоне, критической для разделения, тогда как остальные верно классифицируемые наблюдения обучающей выборки вне этой зоны игнорируются (точнее, являются “резервуаром” для оптимизационного алгоритма).

Если имеется два класса наблюдений и предполагается линейная форма границы между классами, то возможны два случая. Первый из них связан с возможностью идеального разделения данных при помощи некоторой гиперплоскости \(z_k(x) = \sum_{i=1}^p \beta_i x_i + \beta_0\) (двумерный вариант представлен слева на рис. 6.3). Поскольку таких гиперплоскостей может быть множество, то оптимальной является разделяющая поверхность, которая максимально удалена от обучающих точек, т.е. имеющая максимальный зазор \(M\) (margin).

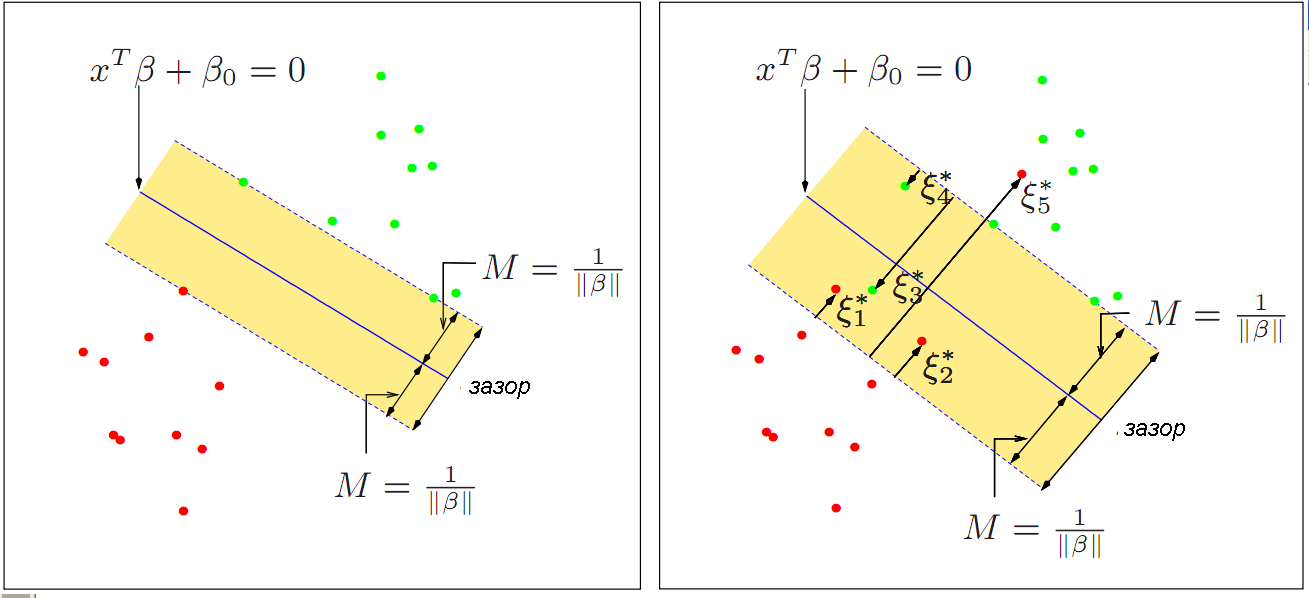
Рисунок 6.3: Классификаторы с минимальным зазором (слева) и на опорных векторах (справа)

На рис. 6.3 справа показан другой случай, когда облако точек перекрывается и оба класса линейно неразделимы. Собственно опорными векторами называются наблюдения, лежащие непосредственно на границе разделяющей полосы, либо на неправильной для своего класса стороне относительно границ зазора (такие точки отмечены \(\xi^*_J\) на рис. 6.2). Для граничных и всех остальных точек принимается \(\xi^*_J = 0\).

Оптимальную разделяющую гиперплоскость такого классификатора \(z_k(x) = \sum_{i=1}^p \beta_i x_i + \beta_0\) также находят из условия максимизации ширины зазора \(M\), но при этом разрешается неверно классифицировать некоторую небольшую группу наблюдений, относящихся к опорным векторам. Для этого задаются дополнительным условием оптимизации \(\sum_j \leq \xi^*_J\), где \(C\) - допустимое число нарушений границы зазора и их выраженность, которое обычно выбирается с использованием перекрестной проверки. Математически поиск решения сводится к удобной задаче квадратичной оптимизации с линейными ограничениями, которая гарантировано сходится к одному глобальному минимуму (Vapnik, 1995; Джеймс и др., 2016).

Поскольку на расположение гиперплоскости оказывают влияние только те наблюдения, которые лежат на границах зазора или нарушают его, то решающее правило такого классификатора довольно устойчиво к выбросам большинства точек, расположенных вне “критической зоны” разделения. Это свойство отличает его от свойств других классификаторов. Например, разделяющая плоскость LDA на рис. 6.2 проводится перпендикулярно дискриминационной функции \(z\) и зависит от средних и ковариационной матрицы, вычисляемых по всем имеющимся наблюдениям.

Для реализации метода опорных векторов в среде R обычно используется функция svm() из пакета e1071. Рассмотрим построение с помощью этой функции линейного классификатора для прогнозирования способа производства стекла по его химическому составу (см. разделы 2.4-2.5, 6.1). Для подбора параметров модели зададим перекрестную проверку с делением исходной выборки на 10 равных частей (cross = 10):

DGlass <- read.table(file = "Glass.txt", sep = ",",
                     header = TRUE, row.names = 1)

DGlass$FAC <- as.factor(ifelse(DGlass$Class == 2, "C2", "C1"))
svm.all <-  svm(formula = FAC ~ ., data = DGlass[, -10], 
                cross = 10, kernel = "linear")  
(table(Факт = DGlass$FAC, Прогноз = predict(svm.all)))

##     Прогноз
## Факт C1 C2
##   C1 72 15
##   C2 27 49

Acc = mean(predict(svm.all) == DGlass$FAC)
paste("Точность=", round(100*Acc, 2), "%", sep = "")

## [1] "Точность=74.23%"

Для подтверждения того, что svm() действительно проводила построение модели с применением кросс-проверки, выполним дополнительно скользящий контроль с использованием самостоятельно составленной функции:

#   Функция для вычисления ошибки перекрестной проверки  
library(e1071)    
CVsvm <- function(x, y) {
    n <- nrow(x)
    Err_S  <- 0 
    for(i in 1:n) {
        svm.temp <- svm(x = x[-i, ], y = y[-i],  kernel = "linear")
        if (predict(svm.temp, newdata = x[i, ]) != y[i]) 
            Err_S <- Err_S + 1 }
    Err_S/n }
Acc <- 1 - CVsvm(DGlass[, 1:9], DGlass$FAC)
paste("Точность=", round(100*Acc, 2), "%", sep = "")

## [1] "Точность=71.17%"

Ошибка предсказания не изменилась, поскольку перекрестная проверка уже выполнялась при построении модели.

Определенным резервом повышения эффективности модели является выбор оптимального набора предикторов. Селекция переменных может быть выполнена несколькими способами:

c помощью известной нам функции stepclass() из пакета klaR, но, в отличии от LDA, здесь необходимо использовать метод построения модели svmlight;
c использованием алгоритма рекурсивного извлечения переменных SVM-RFE (Recursive Feature Extraction Algorithm; Guyon et al., 2002);
на основе функций penalizedSVM или хорошо знакомого нам пакета caret.

Для реализации функций stepclass() и svmlight() из пакета klaR необходимо скачать (http://svmlight.joachims.org) и поместить в рабочую директорию бинарные исполняемые файлы метода SVMlight (Joachims, 1999), написанные на языке C (эти файлы включены в приложения к этой книге):

stepclass(FAC ~ ., data = DGlass[, -10],
          method = "svmlight", pathsvm = "D:/R/SVMlight")

Однако выполнение этой команды оказалось в наших условиях столь продолжительным, что мы не смогли продемонстрировать читателям эту возможность.

Рекурсивное извлечение переменных SVM-RFE происходит с использованием специального критерия, оценивающего релевантность каждого предиктора по отношению к качеству полученного классификатора. Авторы метода (Guyon et al., 2002) написали и предоставили в открытый доступ (http://citeseer.ist.psu.edu) скрипт небольшой функции svmrfeFeatureRanking(), возвращающей ранжированный список переменных. Мы также включили файл с командами этой функции в наш набор скриптов, сопутствующих книге:

source("scripts/SVM-RFE.r")
featureRankedList <- svmrfeFeatureRanking(DGlass[, 1:9], DGlass$FAC)
ErrSvm <- sapply(1:9, function(nf)  {
    svmModel <- svm(DGlass[, featureRankedList[1:nf]],
                    DGlass$FAC, kernel = "linear") 
    mean( predict(svmModel) != DGlass$FAC )  }  )
data.frame(Index = featureRankedList,
           NameFeat = 
               names(DGlass[, featureRankedList]), ErrSvm = ErrSvm)

Отметим, что метод опорных векторов слабо зависит от эффектов коллинеарности предикторов и, по сравнению с LDA, значительно меньше переменных было исключено из модели как малоинформативные. Построим гиперплоскость на основе 7 отобранных признаков:

DGlass.sel <- DGlass[, c(featureRankedList[1:7], 11)]
(svm.sel <- svm(formula = FAC ~ ., data = DGlass.sel, cross = 10,
                kernel = "linear", prob = TRUE))
table(Факт = DGlass.sel$FAC, Прогноз = predict(svm.sel))
Acc = mean(predict(svm.all) == DGlass$F )
paste("Точность=", round(100*Acc, 2), "%", sep = "")

Действительно, число правильно классифицированных образцов оказалось на 4 единицы больше, чем при полном наборе признаков.

Рассмотрим процедуры селекции признаков и тестирования моделей с использованием пакета caret. Обратим внимание, что для построения модели опорных векторов здесь используется функция svm() из другого пакета - kernlab:

svmProfile <- rfe(DGlass[, 1:9], DGlass$FAC, sizes = 2:9,
                  rfeControl = rfeControl(functions = caretFuncs,
                                          method = "cv"), method = "svmLinear")

Информативный набор предикторов, полученный методом рекурсивного исключения, состоит из 5 признаков.

Выполним тестирование моделей на основе разного числа предикторов (9, 7 и 5) с использованием показателя AUC (площади под ROC-кривой - см. раздел 2.4), для чего в trainControl() зададим параметр summaryFunction = twoClassSummary:

ctrl <- trainControl(method = "repeatedcv", repeats = 5,    
                     summaryFunction = twoClassSummary, classProbs = TRUE)
print(" Модель на основе всех 9 предикторов ")

## [1] " Модель на основе всех 9 предикторов "

train(DGlass[, 1:9], DGlass$FAC, method = "svmLinear",
      metric = "ROC", trControl = ctrl)

## Support Vector Machines with Linear Kernel 
## 
## 163 samples
##   9 predictor
##   2 classes: 'C1', 'C2' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 147, 147, 147, 146, 147, 146, ... 
## Resampling results:
## 
##   ROC        Sens       Spec     
##   0.7505109  0.7855556  0.5785714
## 
## Tuning parameter 'C' was held constant at a value of 1
##

print(" Модель на основе 7 предикторов ")

## [1] " Модель на основе 7 предикторов "

train(DGlass[, c(4,6,9,8,3,5,7)], DGlass$FAC,
      method = "svmLinear", metric = "ROC", trControl = ctrl)

## Support Vector Machines with Linear Kernel 
## 
## 163 samples
##   7 predictor
##   2 classes: 'C1', 'C2' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 147, 147, 147, 146, 146, 147, ... 
## Resampling results:
## 
##   ROC       Sens       Spec     
##   0.766627  0.8041667  0.6267857
## 
## Tuning parameter 'C' was held constant at a value of 1
##

print(" Модель на основе 5 предикторов ")

## [1] " Модель на основе 5 предикторов "

train(DGlass[, c(4,6,9,8,5)], DGlass$FAC, method = "svmLinear",
      metric = "ROC", trControl = ctrl)

## Support Vector Machines with Linear Kernel 
## 
## 163 samples
##   5 predictor
##   2 classes: 'C1', 'C2' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 147, 147, 146, 147, 146, 148, ... 
## Resampling results:
## 
##   ROC        Sens  Spec     
##   0.7027629  0.78  0.5410714
## 
## Tuning parameter 'C' was held constant at a value of 1
##

Последняя модель на основе RFS-метода оказалась наименее качественной по AUC, но имеет наибольшую чувствительностью Sens.