9.3 Методы ординации объектов и переменных: построение и сравнение диаграмм
Ординация в узком смысле представляет собой нахождение таких координатных осей на плоскости, относительно которых можно выполнить оптимальное проецирование многомерных анализируемых объектов. Ординация связана с поиском наиболее “естественных” системных закономерностей и особенно эффективна при наличии комплекса взаимно скоррелированных влияющих факторов, “которые являются кошмаром, например, для множественной регрессии”. К настоящему времени в среде R разработано и реализовано значительное количество алгоритмов сжатия информационного пространства, в частности:
- метод главных компонент PCA (см. раздел 2.4), оперирующий с ковариационной (корреляционной) матрицей;
- метод главных координат PCoA и неметрическое многомерное шкалирование (NMDS, nonmetric multidimensional scaling), выполняющие последовательную процедуру преобразования любой матрицы дистанций;
- анализ соответствий или корреспондентный анализ (CA, correspondence analysis), основанный на итерационной процедуре встречного усреднения взвешивающих коэффициентов для объектов и переменных (Джогман и др., 1999);
- функции многомерного факторного анализа, включая версии для иерархических и смешанных данных, представленные в пакете
FactoMineR.
Метод главных координат PCoA, или многомерное шкалирование (MDS, multidimensional scaling), во многом похож на РСА, но вместо корреляционной матрицы выполняет вычисление собственных значений и собственных векторов произвольной квадратной симметричной матрицы расстояний \(\mathbf{D}\). Так можно компенсировать некоторые отклонения от предпосылок в отношении статистического распределения данных, принятых для корреляционного анализа, но одновременно возникает проблема выбора подходящей метрики дистанции. На странице gastonsanchez.com описана работа с 7 функциями различных пакетов R, в которых реализован метод PCoA, но обычно используют базовую функцию cmdscale().
В качестве примера рассмотрим достаточно представительный набор геоботанических данных bryceveg из пакета labdsv, в котором 165 видов травянистой растительности было обнаружено на 160 пробных площадках, заложенных на территории Брайс-Каньон (Bryce Canyon, штат Юта, США):
library(labdsv)
data(bryceveg)
data(brycesite)
# Рассчитываем три матрицы расстояний по разным формулам
dis.mht <- dist(bryceveg, "manhattan")
dis.euc <- dist(bryceveg, 'euclidean')
dis.bin <- dist(bryceveg, "binary")
# Создаем объекты cmdscale
mht.pco <- cmdscale(dis.mht, k = 10, eig = TRUE)
euc.pco <- cmdscale(dis.euc, k = 10, eig = TRUE)
bin.pco <- cmdscale(dis.bin, k = 10, eig = TRUE)
# График изменения относительных собственных чисел
plot(1:10, (mht.pco$eig/sum(mht.pco$eig))[1:10],
type = "b", xlab = "Число координат",
ylab = "Относительные собственные значения")
lines((euc.pco$eig/sum(euc.pco$eig))[1:10], type = "b", col = 2)
lines((bin.pco$eig/sum(bin.pco$eig))[1:10], type = "b", col = 3)
legend("topright", c("Манхэттен", "Евклид", "Хемминг"), lwd = 1, col = 1:3)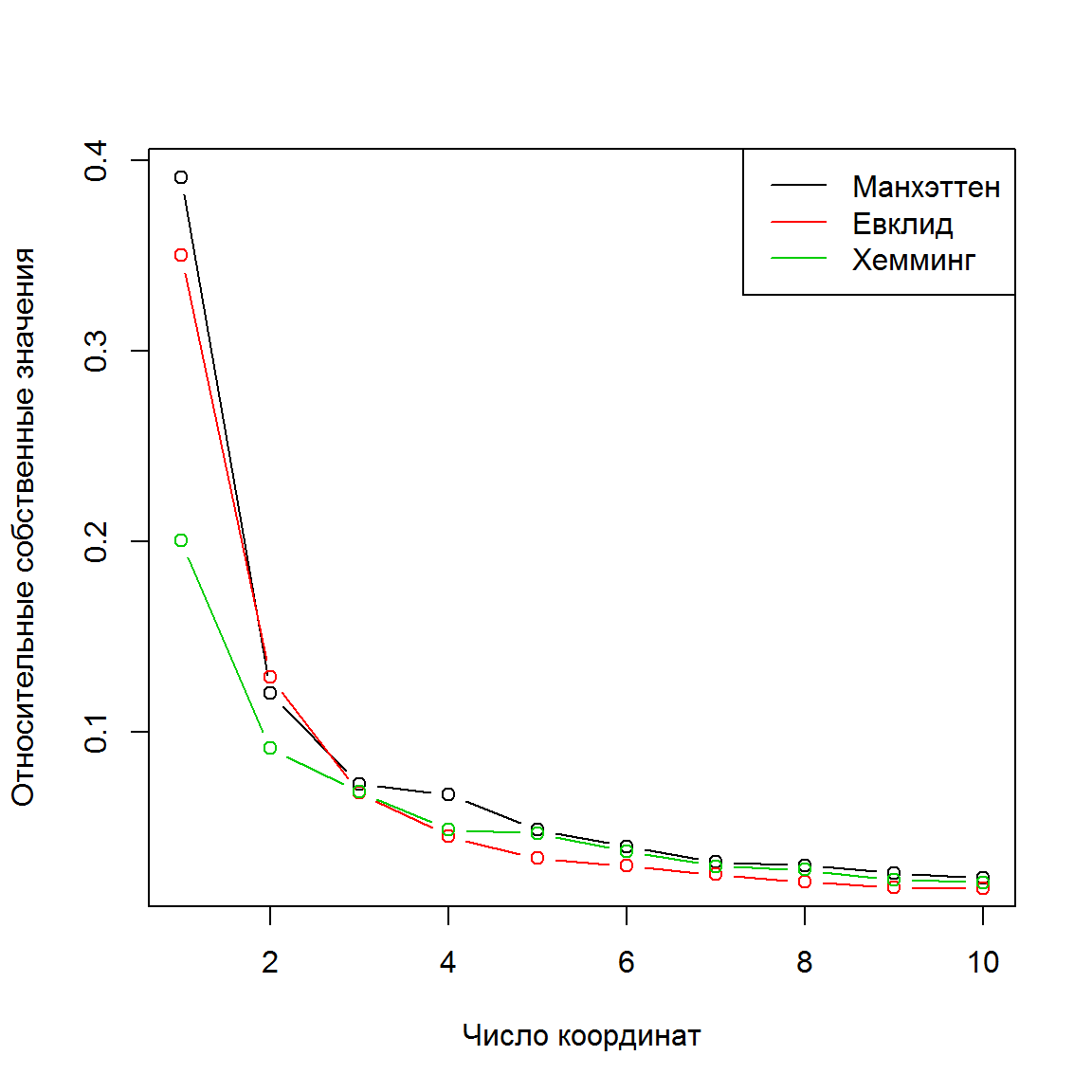
Рисунок 9.4: Уменьшение собственных значений матриц с увеличением числа координат
Возникает естественный вопрос, какая из трех наиболее характерных метрик расстояния приводит к наилучшей ординации? Если ориентироваться на величину первых двух собственных значений матрицы \(\mathbf{D}\) (рис. 9.4), которые соответствуют доле объясненной дисперсии видовой структуры участков, то наименее адекватной оказывается ординация, полученная при использовании расстояния Хемминга, т.е. когда учитывалось только наличие или отсутствие видов растений. Второй способ - оценить коэффициент корреляции двух матриц расстояния: исходной и рассчитанной на основе первых двух главных координат, что соответствует доле информации, сохраненной после сжатия 165-мерного пространства до двумерного. Наконец, всегда полезно просто посмотреть на характер распределения точек на выполненной проекции и прислушаться к голосу собственной интуиции (рис. 9.5):
par(mfrow = c(1, 2))
plot(euc.pco$points[, 1:2], col = 4, pch = 17, xlab = "PCO1",
ylab = "PCO2", main = "Расстояние Евклида")
plot(0 - bin.pco$points[, 1:2], col = 3, pch = 17, xlab = "PCO1",
ylab = "PCO2", main = "Расстояние Хемминга")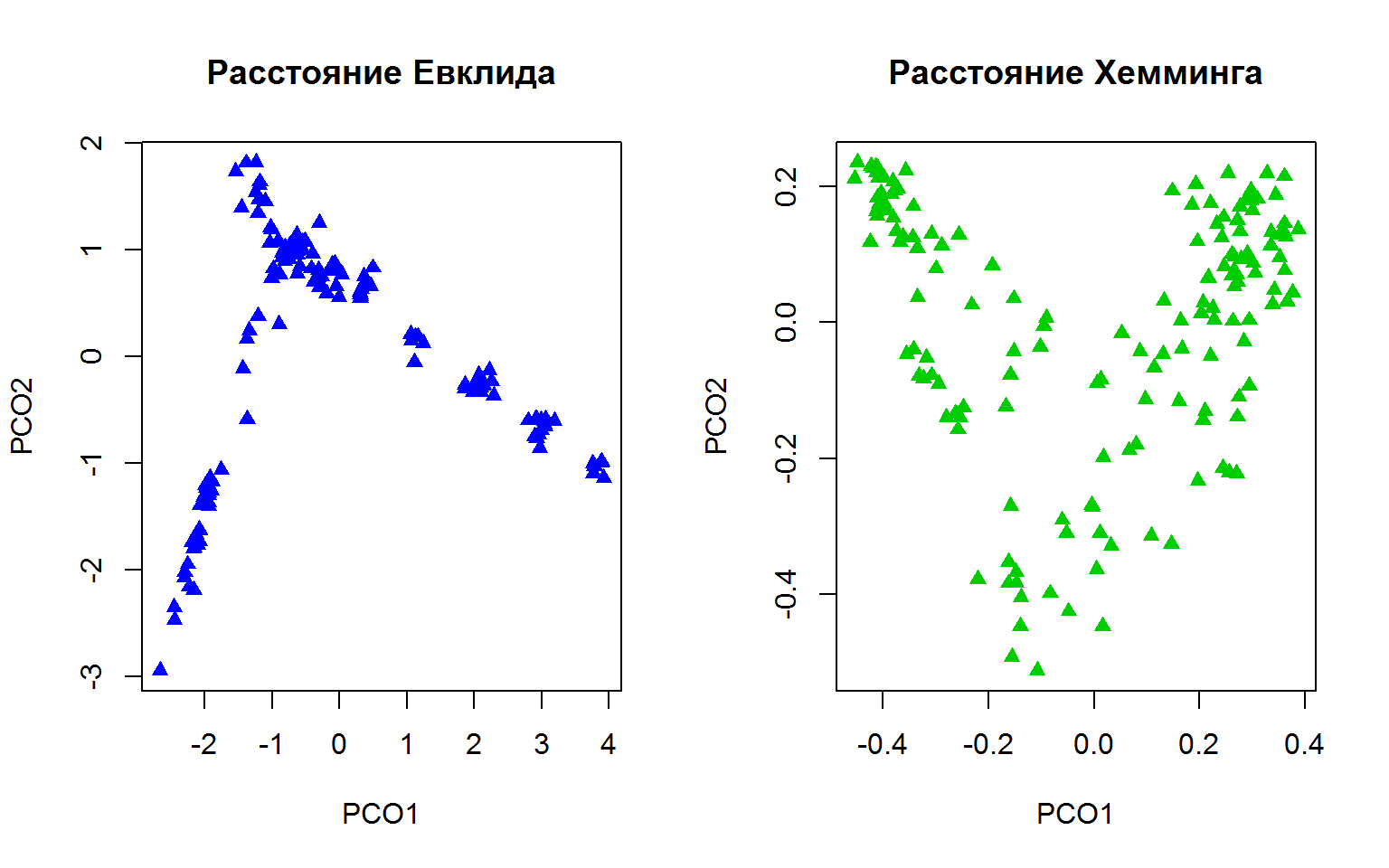
Рисунок 9.5: Распределение точек ординации PCoA для разных метрик дистанции
CCor <- c(cor(dis.euc, dist(euc.pco$points[, 1:2], 'euclidean')),
cor(dis.mht, dist(mht.pco$points[, 1:2], 'manhattan')))
names(CCor) <- c("Евклидово", "Манхэттенское")
print(CCor)## Евклидово Манхэттенское
## 0.8171305 0.8256334Важной косвенной оценкой, насколько полученная ординация адекватна задаче исследования, является ее тесная взаимосвязь с ведущими внешними факторами. Функция ordtest() из пакета labdsv выполняет оценку \(p\) значимости такой связи с использованием рандомизационного теста, рассчитывая сумму квадратов разностей двух матриц расстояния (исходной и построенной на основе фактора). Другой подход основан на аппроксимации двумерной сглаживающей поверхностью значений предиктора в точках, определенных главными координатами. Подробности изложены в курсе лекций проф. Д. Робертса студентам университета штата Монтана (http://ecology.msu.montana.edu). Ниже используется функция surf(), которая выполняет сглаживание сплайнами и визуализацию на диаграмме линий изоном фактора. Ее скрипт приведен в лекции №8 и скопирован нами в файл surf_pso.r:
data(brycesite)
H <- brycesite$elev
mht.pco <- pco(dis.mht, k = 2) # аналог функции cmdscale()
source("scripts/surf_pco.R")
plot(mht.pco, pch = 16, col = "red")
surf.pco(mht.pco, H, col = "blue")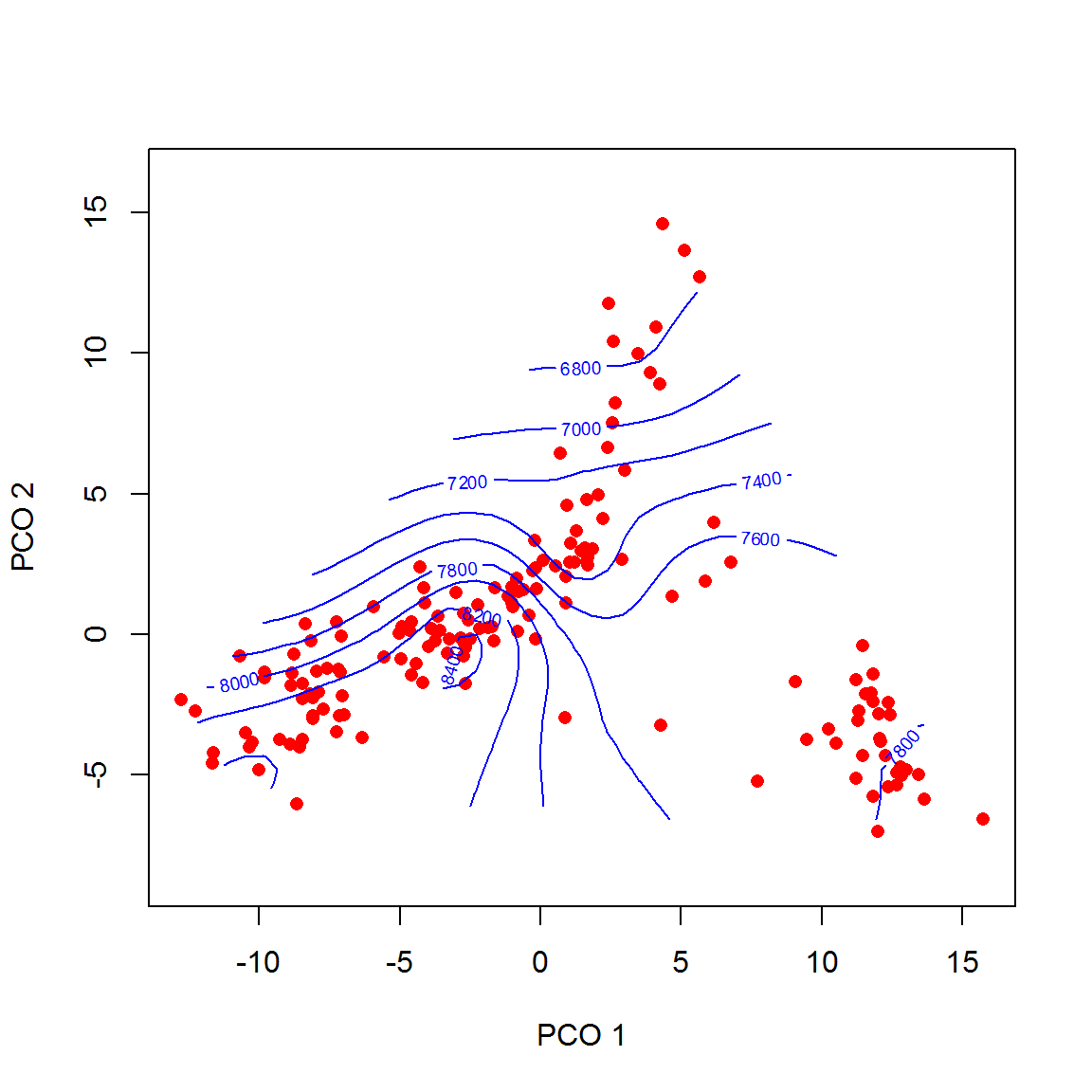
Рисунок 9.6: Ординация геоботанических данных с использованием манхэттенского расстояния и ее связь с высотой пробных площадок
##
## Family: gaussian
## Link function: identity
##
## Formula:
## var ~ s(x, y)
##
## Estimated degrees of freedom:
## 16.1 total = 17.08
##
## GCV score: 189195.3
## D^2 = 0.5999ordtest(mht.pco, H)$p## [1] "H < 0.001"## [1] 0.001Для построения сглаживающей поверхности высоты участков над уровнем моря по осям двух главных координат использовалась функция gam() из пакета mgcv, выполняющая аппроксимацию сплайном s(x, y). Качество подгонки может быть оценено с помощью псевдо-коэффициента детерминации, который для произвольной GAM-модели m рассчитывается как D2 = (m$null.deviance - m$deviance)/m$null.deviance.
Если построить различные варианты ординации с использованием разных методов или метрик, то наилучшей будет считаться та, которая доставляет максимум D2. При этом, разумеется, необходимо выбрать для тестирования ведущий внешний фактор. Например, если вместо высоты над уровнем моря использовать угол наклона площадки к горизонту brycesite$av, то его статистическая связь с изменчивостью видового состава растительности будет незначимой р=0.544, а величина D2 будет мала D^2 = 0.06873.
Для детального сравнения двух диаграмм их необходимо привести к единой форме, т.е. к стандартной конфигурации, которая будет независима от положения, масштаба и поворота координатных осей. Один из способов сравнения графиков заключается в “прокрустовом” преобразовании геометрии точек. Для этого проводится ряд последовательных итераций подгонки масштаба осей:
- cравниваемые точки помещаются внутри единичного круга \(|\delta| = 1\);
- вся структура вращается относительно центра координат;
- находится минимум суммы квадратов расстояний между двумя ординациями \(m^2 = [\mathbf{x}_1 - T(\mathbf{x}_2)]^2 \rightarrow \min\) или максимум прокрустовой корреляции \(r = \sqrt{1 - m^2}\).
Используя функции из пакета vegan, выполним сравнение расположения площадок на двух диаграммах, построенных методами главных координат (mht.pco на рис. 9.6) и анализом соответствий CA:
library(vegan)
ca <- cca(bryceveg)
pro.comp <- procrustes(mht.pco, ca)
plot(pro.comp)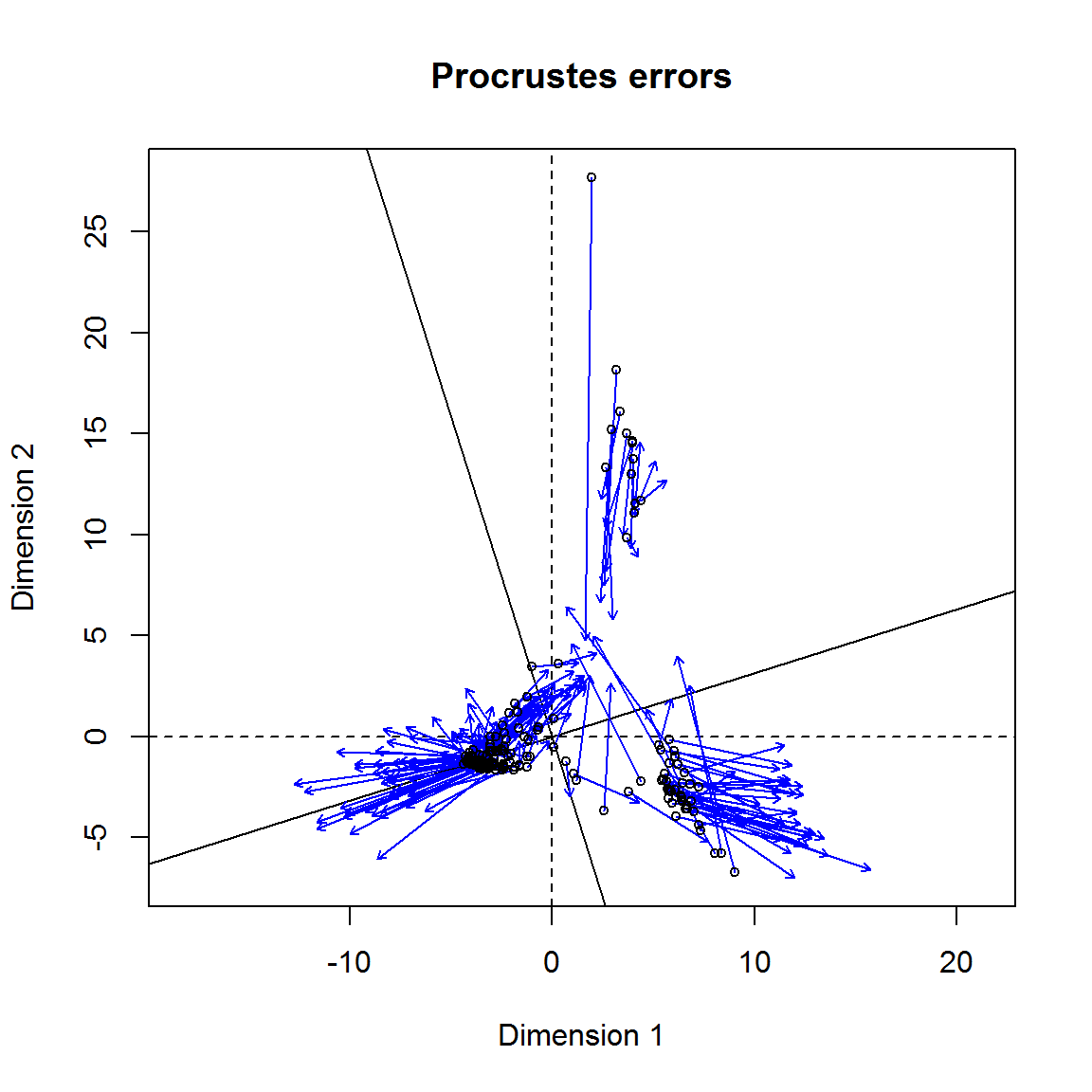
Рисунок 9.7: Сравнение двух диаграмм после прокрустового преобразования
Использование линейных преобразований в ходе проецирования на плоскость дает возможность не только построить упорядоченную диаграмму объектов, но и выполнить ординацию переменных, использованных в анализе. В случае главных компонент взаимный пересчет координат легко сделать по формулам:
\[F_s(i) = 1/\sqrt{\lambda_s}\sum_{k} x_{ik}G_s(k); \quad G_s(k) = 1/\sqrt{\lambda_s}\sum_i x_{ik}F_s(i),\]
где \(F_s(i)\) и \(G_s(k)\) - координаты \(i\)-го объекта и \(k\)-й переменной на \(s\)-й оси компоненты, а \(\lambda_s\) – собственное значение, связанное с \(s\)-й осью.
В случае анализа соответствий такая диаграмма для 165 видов на территории Брайс-Каньо́н выглядит как на рис. 9.8:
plot(ca, type = "n") # Отрисовка «пустой» диаграммы
ordilabel(ca, dis = "sp", cex = 0.7, font = 3, add = TRUE)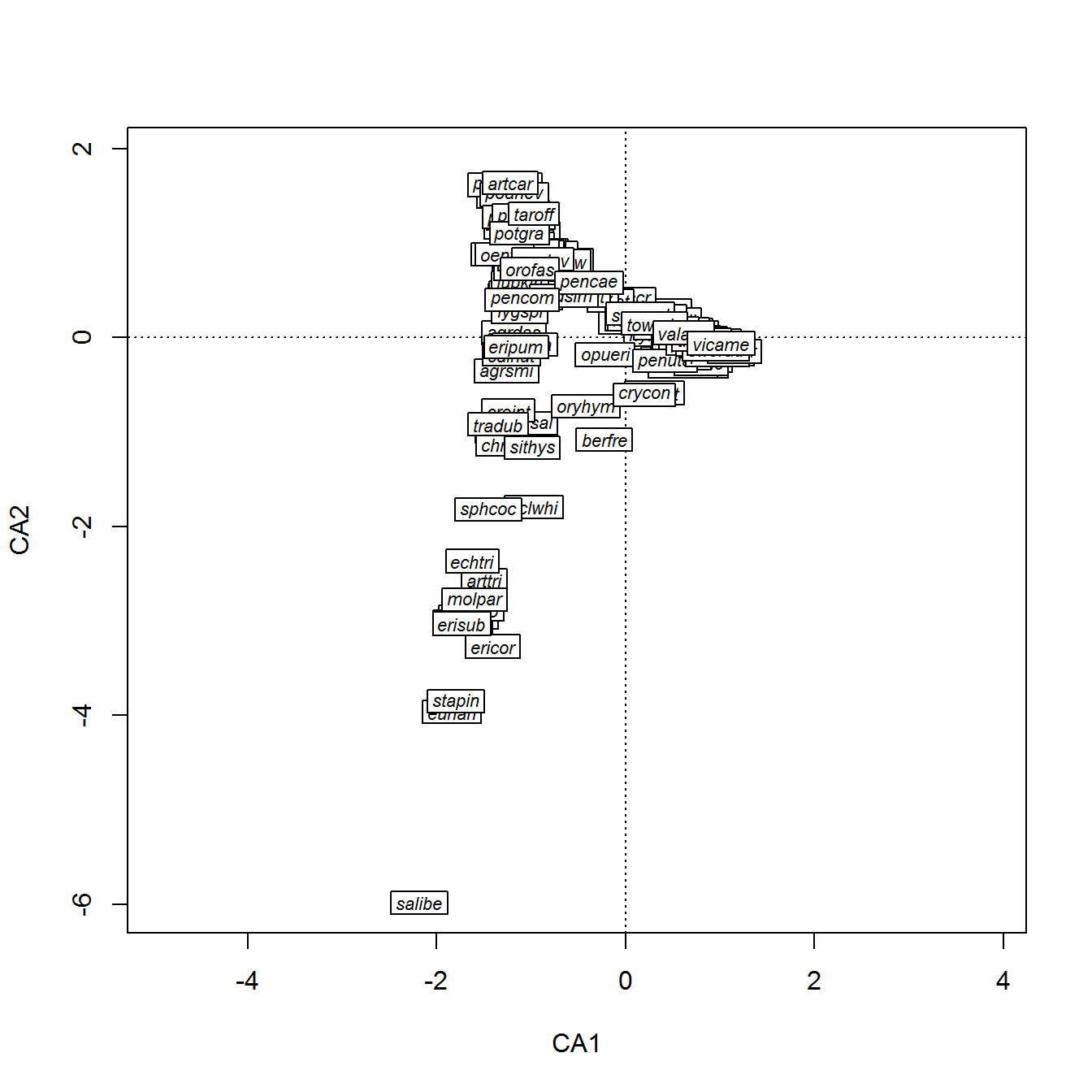
Рисунок 9.8: Ординационная диаграмма видов растительности, полученная методом анализа соответствий
Если вид встречается только в одном месте, то его положение на диаграмме совпадает с точкой, обозначающей соответствующую пробную площадку. В противном случае местоположение вида в системе осей СА1-СА2 определяется средневзвешенными координатами нескольких его возможных местообитаний. По-видимому, эта точка определяет экологический оптимум вида, где его появление наиболее вероятно, либо обилие максимально.
Функции ordipointlabel() и ordilabel() из пакета vegan дают возможность расположить на графике метки данных наилучшим образом и задать последовательность их визуализации: в верхнем слое диаграммы на рис. 9.8 показаны экологически важные виды с наибольшей суммой обилия по столбцам.
Важное место в современном статистическом анализе занимает построение внешне элегантных и информационно насыщенных графиков. Ведущая роль при этом отводится системе визуализации ggplot2 (Мастицкий, 2016). В предыдущих главах мы приводили ординационные диаграммы, полученные с использованием функций ggplot (см. рис. 2.10, 2.11, 2.13, 7.3, 7.7), когда обсуждали метод главных компонент и дискриминантный анализ. Но читатель, вероятно, смог заметить, что построение графиков ggplot2 - непростой, хотя и увлекательный процесс.
Возможность построения элегантных графиков “одной строкой” предоставляется специализированными пакетами, использующими “в темную” инструментарий графической системы ggplot2. К таким относится пакет factoextra, предназначенный для визуализации результатов многомерного и кластерного анализа (см. также главу 10). Подробный рассказ об этом пакете см. на сайте http://www.sthda.com (STHDA, Statistical tools for high-throughput data analysis).
Функция viz_pca() из пакета factoextra осуществляет построение ординационных диаграмм для объектов и/или переменных (отдельно или совмещенно) на основе PCA-объектов, полученных функциями prcomp(), princomp(), PCA() из пакета FactoMineR и некоторых других.
Набор данных decathlon из пакета FactoMineR (Le et al., 2008) содержит результаты 41 ведущего десятиборца, показанные в 2004 г. на олимпийских играх и турнире “ДекаСтар”. Выполним его PCA-ординацию:
library(FactoMineR)
library(factoextra)
data("decathlon")
colnames(decathlon) <- c("100м", "Длина.прыжок", "Ядро", "Высота.прыжок",
"400м", "110м.барьер", "Диск", "Шест.прыжок",
"Копье", "1500м", "Место", "Очки", "Соревнование")
res.pca <- PCA(decathlon[, 1:10], scale.unit = TRUE, ncp = 3, graph = FALSE)
head(res.pca$eig)## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 3.2719055 32.719055 32.71906
## comp 2 1.7371310 17.371310 50.09037
## comp 3 1.4049167 14.049167 64.13953
## comp 4 1.0568504 10.568504 74.70804
## comp 5 0.6847735 6.847735 81.55577
## comp 6 0.5992687 5.992687 87.54846Первые две компоненты объясняют только 50% статистического разброса результатов. Вклад (contribution) каждой переменной при формировании каждой главной компоненты может быть оценен как отношение квадрата факторной нагрузки (score) к соответствующему собственному значению (Abdi, Williams, 2010). Построим ординационную диаграмму признаков (т.е. видов спорта в десятиборье), но их координаты обозначим не точкой, а стрелкой из начала координат, причем цвет стрелки определим в зависимости от важности каждой переменной:
res.pca$var$contrib## Dim.1 Dim.2 Dim.3
## 100м 18.34376957 2.016090 2.42049891
## Длина.прыжок 16.82246707 6.868559 2.36319121
## Ядро 11.84353954 20.606785 0.03890276
## Высота.прыжок 9.99788710 7.063694 4.79362526
## 400м 14.11622887 18.666374 1.23027094
## 110м.барьер 17.02011495 3.013382 0.61083225
## Диск 9.32848615 21.162245 0.13131711
## Шест.прыжок 0.07745541 1.872547 34.06090024
## Копье 2.34696326 5.784369 10.80714169
## 1500м 0.10308808 12.945954 43.54331962fviz_pca_var(res.pca, col.var = "contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE) # Раскрасим также текст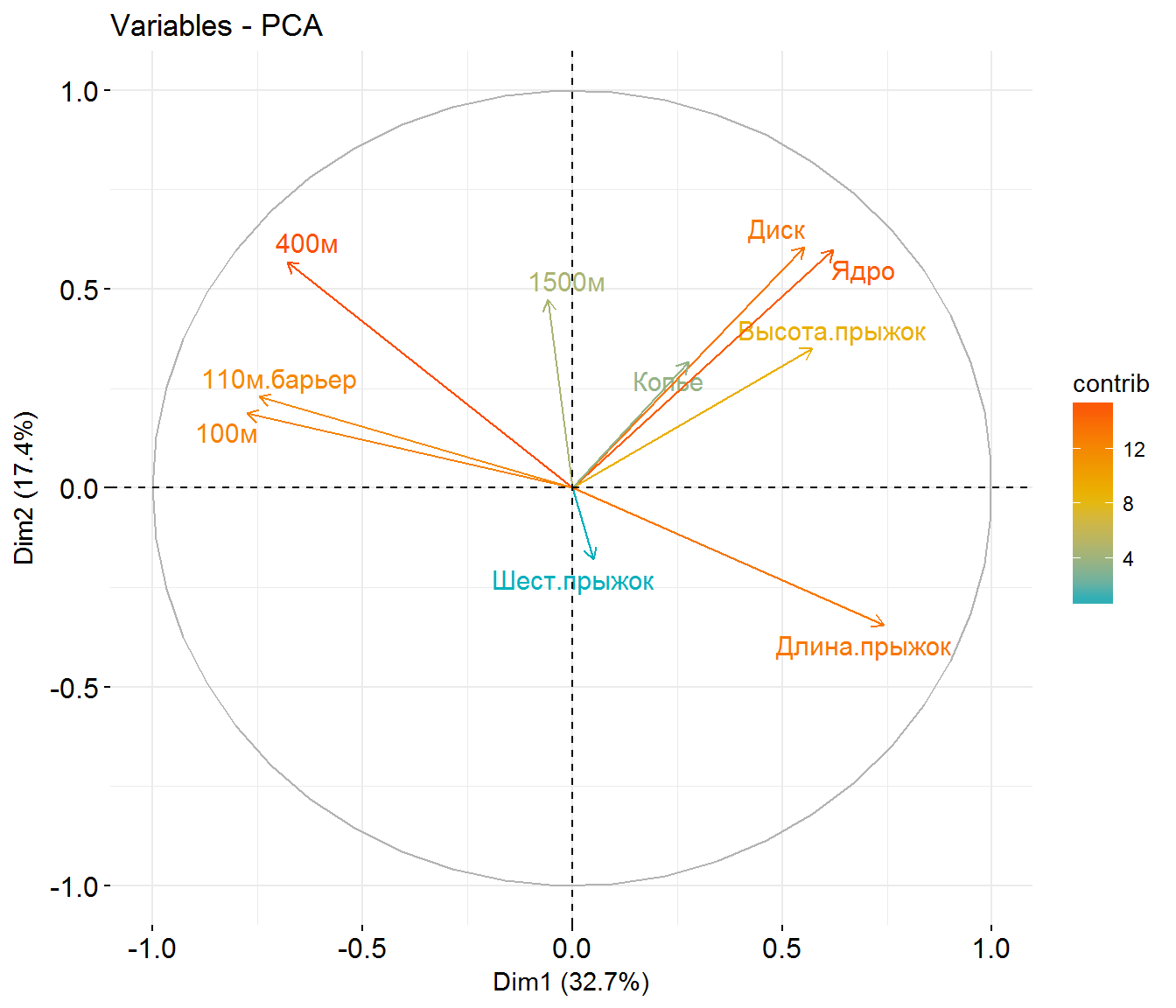
Рисунок 9.9: Ординационная диаграмма видов соревнований в десятиборье
По сути примера видно, что первая компонента связана с темповыми видами спорта (бег на короткие дистанции), а вторая - с силовыми (метание диска и ядра).
Оценим теперь, имеются ли различия между результатами, показанными на Олимпиаде и на турнире “ДекаСтар”. Для этого в структуру объекта PCA включим в качестве вспомогательных переменных признаки, не участвующие в построении ординации (рис. 9.10):
res.pca <- PCA(decathlon, quanti.sup = 11:12, quali.sup = 13, graph = FALSE)
fviz_pca_ind(res.pca, geom = "point", habillage = 13,
addEllipses = TRUE, ellipse.level = 0.68) +
scale_color_brewer(palette = "Dark2") + theme_minimal()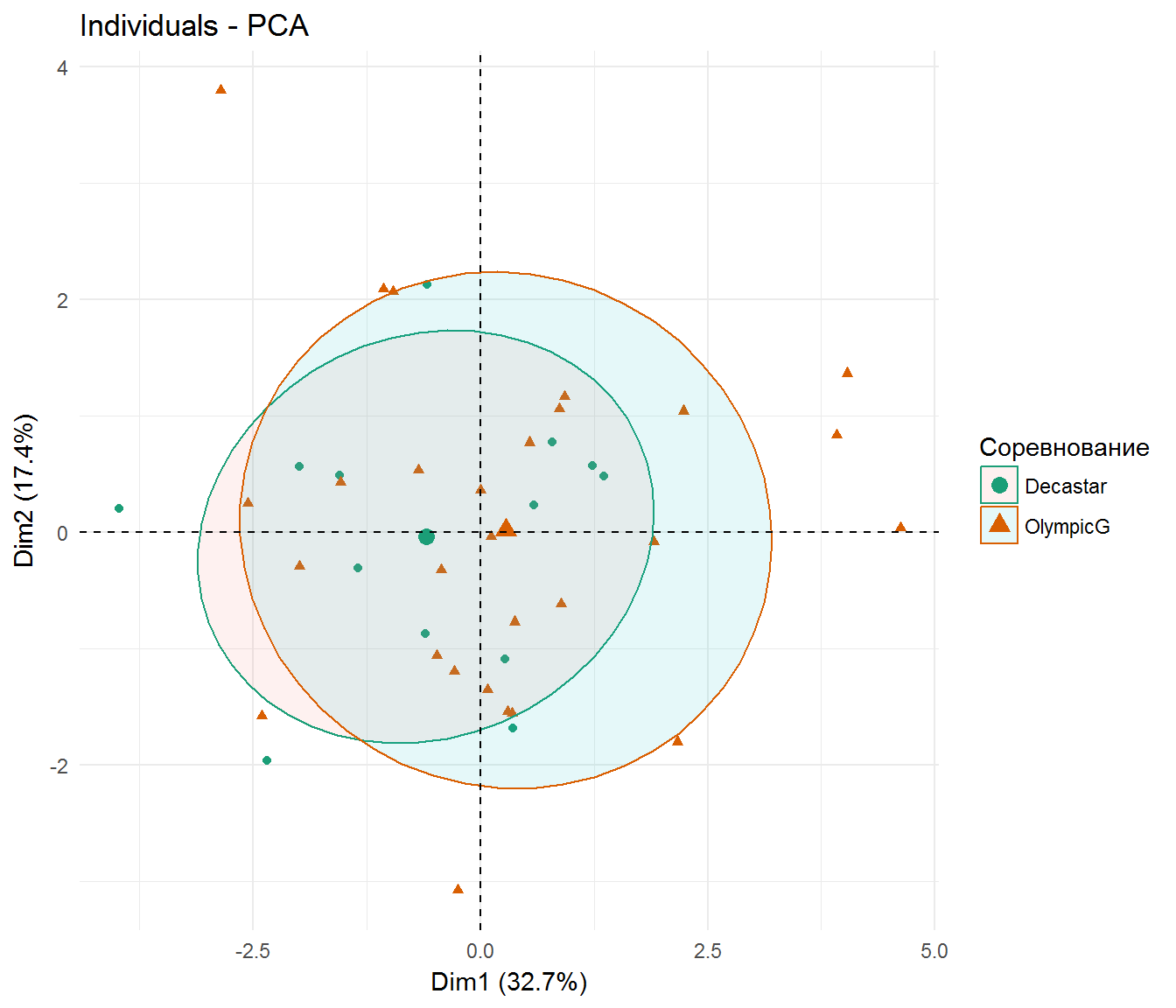
Рисунок 9.10: Ординационная диаграмма участников соревнований в десятиборье
Нетрудно убедиться в том, что по оси первой главной компоненты обозначился “зазор” между групповыми центроидами и результаты, показанные на Олимпиаде, можно считать существенно более высокими. В то же время, разброс показателей на турнире “ДекаСтар” оказался меньше, т.е. состав участников был более однородным.