7.3 Классификация в линейном дискриминантном пространстве
Исходные предпосылки линейного дискриминантного анализа, изложенные нами в разделе 6.1, естественным образом распространяются на случай произвольного числа классов \(k\). Если вновь обратиться к аналогам евклидовой геометрии, то центроиды двух классов определяют положение прямой линии, трех - плоскости, четырех - трехмерной поверхности и т.д. Принцип сводится к тому, что тем самым определяется “натянутое на центроиды” дискриминантное пространство, размерность которого на единицу меньше, чем число классов.
В полученном пространстве необходимо задать точку начала системы координат: наиболее удобен для этого “главный центроид”, занимающий положение, определяемое \(m\)-мерными средними значениями для всей совокупности объектов. Теперь если мы в рассматриваемом пространстве проведем дополнительную ось под некоторым углом, относительно которой средние значения классов разделяются в большей степени, чем для любого другого направления, то получим главную разделяющую ось. Предполагая, что есть более чем два класса, можно ориентировать вторую и последующие дискриминтные оси таким образом, чтобы также было обеспечено максимальное разделение классов, но при дополнительном ограничении - все построенные оси ортогональны между собой.
Такая процедура напоминает анализ главных компонент (см. раздел 2.5) за тем основным отличием, что дискриминантные оси проводятся в направлении максимумов не общей, а межгрупповой изменчивости данных. Ее основным результатом также является совокупность линейных комбинаций исходных переменных, которые называются линейными дискриминантами (linear discriminant, LD) или каноническими переменными (canonical variate), и вычисляются по формуле:
\[LD_k = \sum_{j=1}^m \beta_{kj} (x_j - \bar{x}_j),\]
где \(k\) - номер линейного дискриминанта, \(x_j\) - значение \(j\)-й переменной, \(\bar{x}_j\) - среднее значение \(j\)-й переменной (по всем группам), \(\beta_{kj}\) - весовой коэффициент \(j\)-й переменной в \(k\)-ом линейном дискриминанте; суммирование ведется по \(m\) переменным. Первый дискриминант подбирается таким образом, чтобы максимизировать основные различия между группами, второй и последующие также максимизируют оставшуюся межгрупповую изменчивость, но подбираются ортогонально первому и всем предыдущим. Отсюда следует, что любая каноническая дискриминантная функция \(LD_k\) имеет нулевую корреляцию с \(LD_1, \dots, LD_{g-1}\). Если число групп равно \(g\), то число канонических дискриминантных функций будет на единицу меньше числа групп.
Один из методов поиска оптимальных дискриминантных функций заключается в максимизации отношения межгрупповой вариации к внутригрупповой, т.е. \(\mathbf{B / W \Rightarrow max}\), где \(\mathbf{B}\) - межгрупповая, а \(\mathbf{W}\) - внутригрупповая матрица рассеяния наблюдаемых переменных относительно средних. Тогда нахождение канонических коэффициентов дискриминантных функций сводится к нахождению собственных значений \(\lambda_k\) и векторов \(\mathbf{u}_k\): если спроецировать \(g\) групп \(m\)-мерных выборок на \((g – 1)\)-мерное пространство, порожденное собственными векторами \(\mathbf{u}_k\), то отношение \(\lambda = \mathbf{B / W}\) будет максимальным, т.е. разброс между группами будет наиболее контрастным при заданной внутригрупповой вариации.
Обратимся вновь к распознаванию видов цветков ириса, выборка которых носит имя сэра Р. Фишера, поскольку именно на ней он и продемонстрировал возможности дискриминантного анализа:
require(MASS)
LDA.iris <- lda(formula = Species ~ ., data = iris)
LDA.iris$scaling # Коэффициенты линейных дискриминантов## LD1 LD2
## Sepal.Length 0.8293776 0.02410215
## Sepal.Width 1.5344731 2.16452123
## Petal.Length -2.2012117 -0.93192121
## Petal.Width -2.8104603 2.83918785LDA.iris$svd## [1] 48.642644 4.579983(prop = LDA.iris$svd^2/sum(LDA.iris$svd^2)) ## [1] 0.991212605 0.008787395Последними действиями мы вывели значения \(\lambda\), которые являются отношением межгрупповой дисперсии к внутригрупповой дисперсии, и вычислили долю межгрупповой дисперсии, объясненную каждым линейным дискриминантом. На рис. 7.7 представлена ординационная диаграмма наблюдений в осях LD1-LD2, подобная графику главных компонент на рис. 7.3. Можно обратить внимание на то, что трансгрессия точек между видами практически исчезла, а главная ось дискриминации объясняет 99% межгруппового разброса:
prop <- scales::percent(prop)
pred <- predict(LDA.iris, newdata = iris)
scores <- data.frame(Species = iris$Species, pred$x)
# Выводим ординационную диаграмму
require(ggplot2)
ggplot() + geom_point(data = scores,
aes(x = LD1, y = LD2, shape = Species,
colour = Species), size = 3) +
scale_colour_manual(values = c('purple', 'green', 'blue')) +
labs(x = paste("LD1 (", prop[1], ")", sep = ""),
y = paste("LD2 (", prop[2], ")", sep = "")) + theme_bw()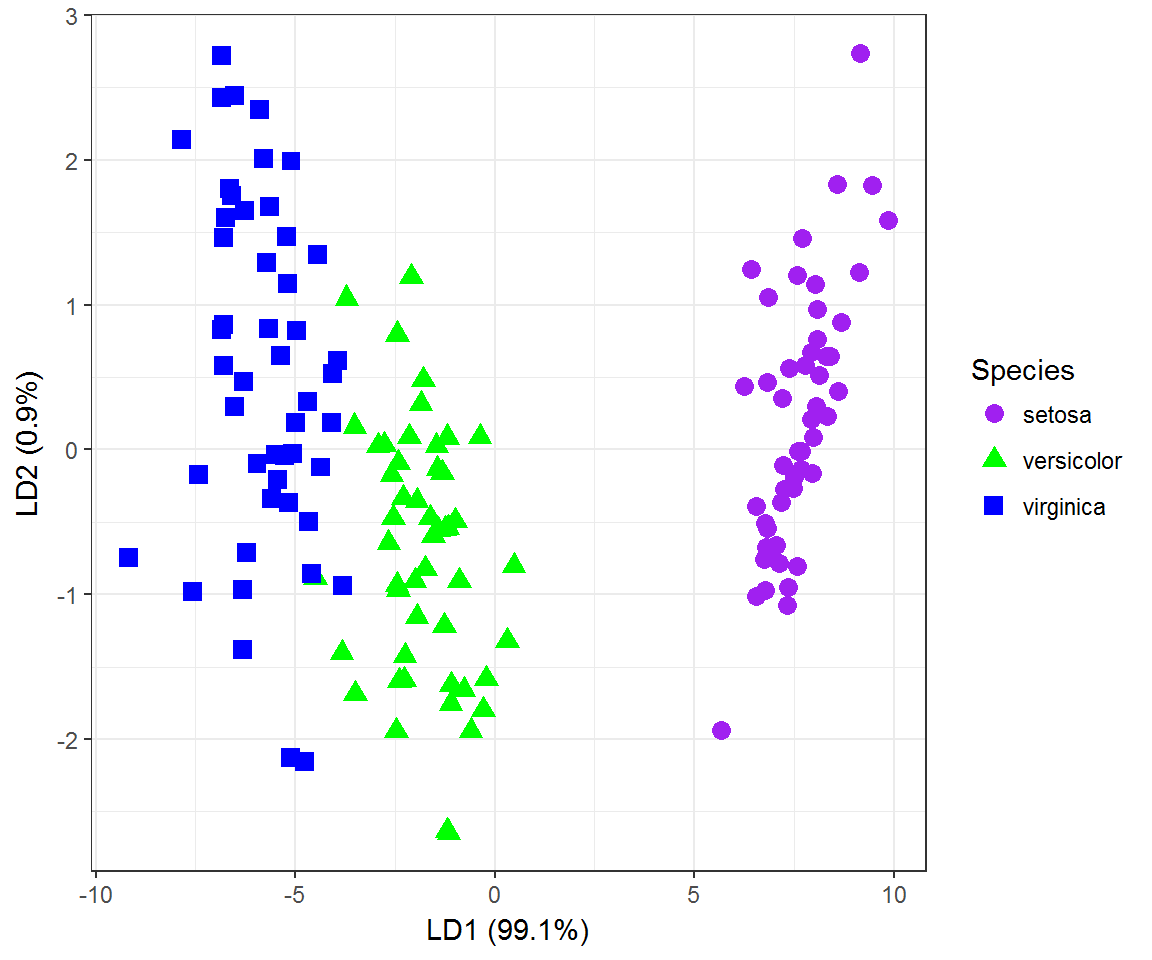
Рисунок 7.7: Ординационная диаграмма выборки ирисов в двух осях линейных дискриминантов
Чтобы оценить относительный вклад отдельных переменных в линейные дискриминанты анализ необходимо проводить с использованием стандартизованных данных. Тогда полученные результаты в плане апостериорной классификации и даже значений линейных дискриминантов для каждого наблюдения не изменятся. Однако, поскольку переменные масштабированы, весовые коэффициенты переменных теперь можно сравнивать между собой: очевидно, что межвидовые различия определяются в первую очередь размерами лепестка:
lda(scale(iris[, 1:4]), gr = iris$Species)$scaling## LD1 LD2
## Sepal.Length 0.6867795 0.01995817
## Sepal.Width 0.6688251 0.94344183
## Petal.Length -3.8857950 -1.64511887
## Petal.Width -2.1422387 2.16413593В результате применения линейного дискриминантного анализа к примерам из обучающей выборки можно сформировать решающее правило, позволяющее отнести новый объект к классу, имеющему наибольшую плотность вероятности (“уровень правдоподобия”) в точке \(\mathbf{x}\) \(m\)-мерного пространства признаков. Сама процедура классификации основана на вычислении апостериорных вероятностей \(P(G_k | x)\) принадлежности произвольного вектора наблюдений \(\mathbf{x}\) к группе \(G_k, k = 1, 2, \dots, g\), с учетом анализа функций плотности распределения \(f_k(х)\).
Величина \(P(G_k | x)\) связана с дистанцией между точкой \(\mathbf{x}\) и \(k\)-м центроидом, и в случае выполнения предпосылок дискриминантного анализа может быть оценена с использованием значений классифицирующих функций:
\[d_k(\mathbf{x}) = \boldsymbol{\mu}_k^T \mathbf{C}^{-1} \mathbf{x} - 0.5 \boldsymbol{\mu}_k^T \mathbf{C}^{-1} \boldsymbol{\mu}_k + \ln \pi_k\]
где \(\mathbf{C}^{-1}\) - матрица, обратная к ковариационной, \(\boldsymbol{\mu}_k\) и \(\ln \pi_k\) вектор средних и априорная вероятность наблюдения объектов \(k\)-го класса соответственно. Объект \(\mathbf{x}\) относится к тому классу \(k\) из \(g\), для которого значение \(d_k\), а следовательно и апостериорная вероятность, максимальны.
Если выделить из обучающей выборки 10 объектов для проверки качества предсказаний, то получим следующие (безошибочные) результаты:
train <- sample(1:150, 140)
LDA.iris3 <- lda(Species ~ ., iris, subset = train)
plda = predict(LDA.iris3, newdata = iris[-train, ])
data.frame(Species = iris[-train, 5], plda$class, plda$posterior)## Species plda.class setosa versicolor virginica
## 5 setosa setosa 1.000000e+00 5.713902e-22 7.458486e-42
## 10 setosa setosa 1.000000e+00 2.930997e-18 1.218099e-37
## 14 setosa setosa 1.000000e+00 4.092905e-19 9.794127e-39
## 18 setosa setosa 1.000000e+00 1.531930e-20 9.414919e-40
## 62 versicolor versicolor 2.002433e-19 9.991156e-01 8.843923e-04
## 76 versicolor versicolor 8.201120e-18 9.999177e-01 8.229471e-05
## 96 versicolor versicolor 6.286548e-17 9.999832e-01 1.677005e-05
## 128 virginica virginica 4.896487e-29 1.353869e-01 8.646131e-01
## 130 virginica virginica 3.544949e-31 1.710826e-01 8.289174e-01
## 137 virginica virginica 2.487518e-43 8.241362e-07 9.999992e-01При анализе всей обучающей выборки цветков ириса мы имеем три ошибочных результата классификации из 150.
Acc <- mean(pred$class == iris$Species)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=98%"Тот же итог мы получим и при проведении скользящего контроля:
LDA.irisCV <- lda(Species ~ ., data = iris, CV = TRUE)
(table(Факт = iris$Species, Прогноз = LDA.irisCV$class))## Прогноз
## Факт setosa versicolor virginica
## setosa 50 0 0
## versicolor 0 48 2
## virginica 0 1 49Acc <- mean(LDA.irisCV$class == iris$Species)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=98%"