9.2 Непараметрический дисперсионный анализ матриц дистанций
Результаты наблюдений, представленные в виде многомерной таблицы объемом \(m \times p\), обычно можно разделить по строкам на r групп, (например, в соответствии со списком регионов, где оценивается покупательский спрос, или шириной водотока, где выполняются гидробиологические пробы). Тогда, в соответствии с моделью дисперсионного анализа, общую изменчивость каждого \(k\)-го фиксированного показателя \(x_k, \, (k = 1, 2, \dots, p)\) можно разложить на компоненты
\[\text{Var}(x_k) = \text{Var}(\tau) + \text{Var}(\epsilon),\]
где \(\text{Var}(\tau)\) - вариация, обусловленная влиянием группирующего фактора, \(\text{Var}(\epsilon)\) - изменчивость, связанная с воздействием неконтролируемых (в том числе случайных) факторов.
Однако, если количество \(p\) одновременно варьируемых показателей велико (например, номенклатура из 300-400 продаваемых товаров), то дисперсионный анализ не дает возможности оценить совокупную изменчивость всего изучаемого многомерного комплекса объектов под воздействием группирующего фактора. Один из приемов избежать “проклятия размерности” - выполнить дисперсионный анализ симметричной матрицы \(\mathbf{D}\) размерностью \(m \times m\), элементами \(d_{ij}\) которой являются коэффициенты расстояния между каждой парой изучаемых объектов \(i\) и \(j\).
Метод, известный как непараметрический многофакторный дисперсионный анализ (npMANOVA), осуществляет разложение многомерной изменчивости, заключенной в матрице расстояний, в соответствии с уровнями влияния изучаемых факторов. В первом приближении, как это показано на рис. 9.1, можно рассчитать общую \(SS_T\) и внутригрупповую \(SS_W\) суммы квадратов \(d_{ij}\), после чего оценить их дисперсионное отношение:
\[SS_T = \frac{1}{m}\sum_{i=1}^{m-1} \sum_{j=i+1}^m d_{ij}; \, \, SS_W = \frac{1}{r}\sum_{i=1}^{m-1} \sum_{j=i+1}^m d_{ij} \omega_{ij}; \, \, F = \frac{SS_W(m-r)}{SS_T(r-1)}, \quad (9.2)\]
где \(\omega_{ij} = 1\), если объекты \(i\) и \(j\) принадлежат одной группе, и \(0\) в противном случае (Anderson, 2001).
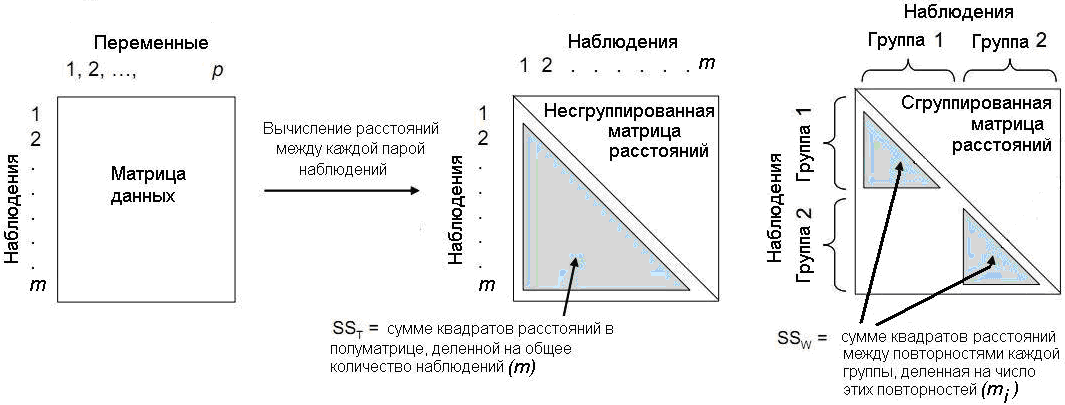
Рисунок 9.1: Схема группировки матрицы расстояний
Более корректный способ вычисления тестовой статистики \(F\) использует ряд конструкций линейной модели ANOVA (McArdle, Anderson, 2001). При применении этого подхода на основе исходной матрицы расстояний \(\mathbf{D}\) с использованием преобразований Гувера рассчитывается матрица \(\mathbf{G}\), описывающая “центроиды”, т. е. центры распределения значений \(d_{ij}\) в пределах каждой группы. Другая проекционная матрица \(\mathbf{H}\) (или “шляпа”, hat) вычисляется с использованием вектора ортогональных контрастов, связанных с уровнями группировочных факторов. Тогда тестовая статистика для проверки нулевой гипотезы об отсутствии различий между \(r\) группами, или псевдо-\(F\)-критерий, находят как
\[F = \frac{tr(\mathbf{HGH})(m-r)}{tr[(\mathbf{I - H})\mathbf{G}(\mathbf{I - H})](r-1)}, \quad (9.3)\]
где \(tr\) - сумма диагональных элементов матрицы, \(\mathbf{I}\) - единичная матрица. При выполнении требований к конфигурации данных и использовании евклидова расстояния обе формулы (9.2) и (9.3) становятся эквивалентными и воспроизводят традиционное дисперсионное отношение Фишера.
Распределение многомерной псевдо-\(F\)-статистики (9.2-9.3) при справедливости нулевой гипотезы теоретически неизвестно, и поэтому для его аппроксимации используется рандомизационная процедура. Ее практическая стратегия состоит в том, чтобы получить большое подмножество значений \(F^*\), извлеченных случайно, независимо и с равной вероятностью из нуль-распределения \(\boldsymbol{F^*}\), полученного в результате многократного хаотичного перемешивания наблюдений относительно выделенных групп. \(Р\)-значение, соответствующее верной нулевой гипотезе, вычисляется как доля значений \(F^*\), которые больше или равны значению \(F\), найденному на реальных данных.
Непараметрический дисперсионный анализ Андерсона реализован в пакетах TraMineR (см. раздел 5.5) или vegan функцией
adonis(formula, data, permutations = 999, method = "bray"),
где объект formula чаще всего имеет форму Y ~ A + B*C, в которой Y - таблица исходных данных, которая пересчитывается в матрицу дистанций по выражению method, а A, B и C - независимые (“объясняющие”) факторы или непрерывные переменные. Если факторные пространства являются непересекающимися по какому-то показателю, то, указав его в качестве параметра strata, можно выполнить гнездовой дисперсионный анализ (nested ANOVA).
Рассмотрим проведение анализа на примере таблицы dune, которая содержит данные по 20 пробным участкам, заложенным в дюнах одного датского острова, на которых было обнаружено 30 видов луговой травянистой растительности. Обилие каждого вида оценивалось в баллах проективного покрытия от 0 до 7. Параллельно для каждого участка измерялась толщина гумусового слоя почвы A1 и оценивалась одна из 4-х категорий Management агротехнических мероприятий по улучшению травостоя (таблица dune.env):
library(vegan)
data(dune)
data(dune.env)
(results <- adonis(dune ~ Management*A1, data = dune.env, permutations = 499))##
## Call:
## adonis(formula = dune ~ Management * A1, data = dune.env, permutations = 499)
##
## Permutation: free
## Number of permutations: 499
##
## Terms added sequentially (first to last)
##
## Df SumsOfSqs MeanSqs F.Model R2 Pr(>F)
## Management 3 1.4686 0.48953 3.2629 0.34161 0.002 **
## A1 1 0.4409 0.44089 2.9387 0.10256 0.034 *
## Management:A1 3 0.5892 0.19639 1.3090 0.13705 0.240
## Residuals 12 1.8004 0.15003 0.41878
## Total 19 4.2990 1.00000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Традиционная таблица дисперсионного анализа полученных результатов показывает статистическую значимость обоих основных факторов и незначимость эффекта их парного взаимодействия. Например, \(р\)-значение, равное 0.018, означает, что только в 9 случаях из 500 имитируемое значение \(F^*\), полученное при справедливости нулевой гипотезы, превысило значение \(F\), вычисленное по (9.3) для эмпирических данных.
Для однофакторного дисперсионного анализа и оценки однородности многомерной вариации в группах наблюдений удобно использовать также другую функцию vegan - betadisper(), на вход которой подается произвольная матрица дистанций d. Выполним расчеты с применением этой функции на основе группировочного фактора group = Management:
D <- vegdist(dune)
# Предварительно рассчитываем матрицу расстояний Брея-Кёртиса D <- vegdist(dune)
mod <- betadisper(D, dune.env$Management, type = "centroid")
plot(mod, hull = FALSE, main = "")
legend("topright", levels(dune.env$Management), pch = 1:4, col = 1:4)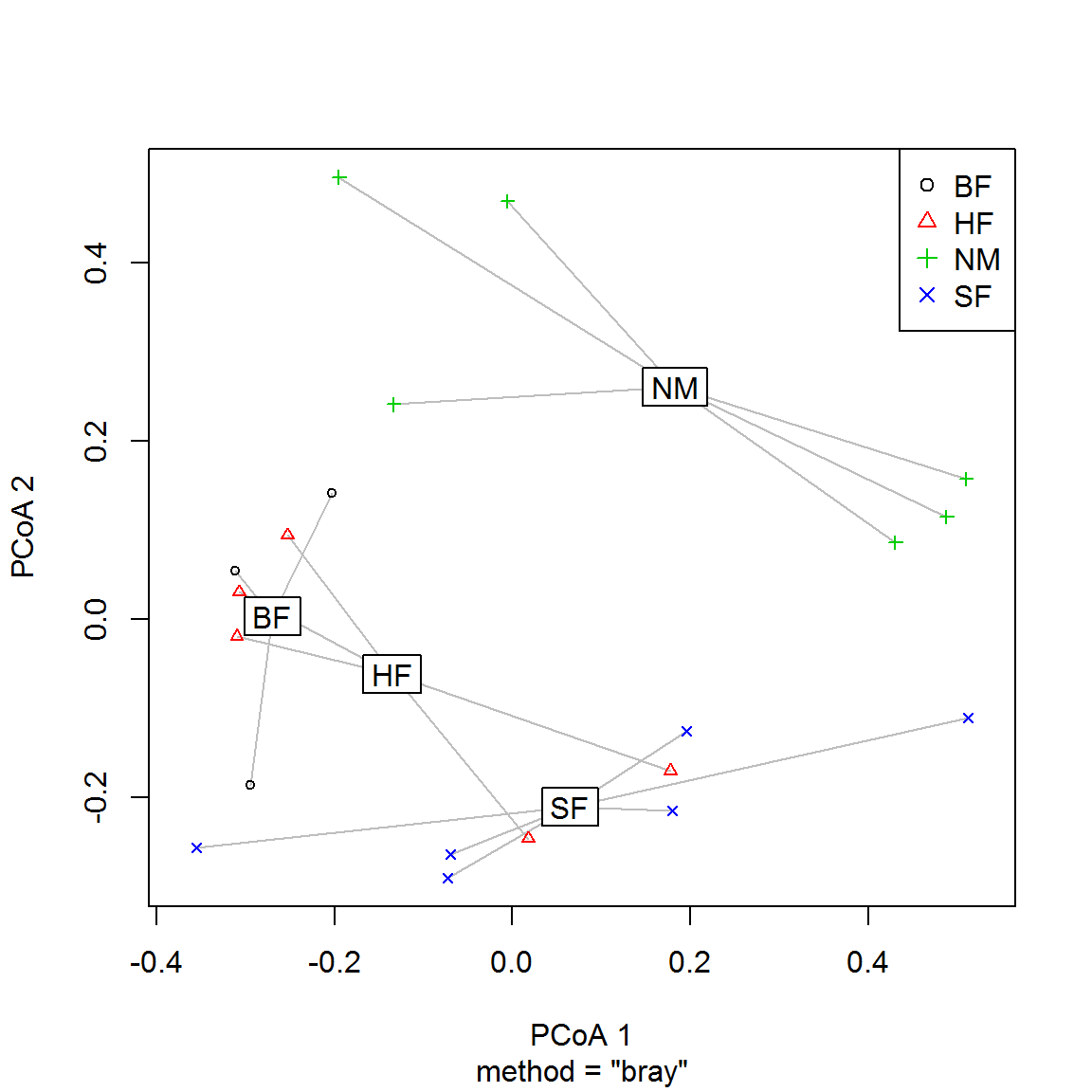
Рисунок 9.2: Центроиды групп в пространстве двух главных координат
set.seed(202)
# Выполнение рандомизационного теста и парных сравнений
permutest(mod, pairwise = TRUE)##
## Permutation test for homogeneity of multivariate dispersions
## Permutation: free
## Number of permutations: 999
##
## Response: Distances
## Df Sum Sq Mean Sq F N.Perm Pr(>F)
## Groups 3 0.12457 0.041525 3.8687 999 0.038 *
## Residuals 16 0.17174 0.010733
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Pairwise comparisons:
## (Observed p-value below diagonal, permuted p-value above diagonal)
## BF HF NM SF
## BF 0.3490000 0.0050000 0.220
## HF 0.3698273 0.0050000 0.276
## NM 0.0047822 0.0040127 0.219
## SF 0.2094850 0.2982378 0.2391828В целом перестановочный тест показал значимое (р = 0.038) влияние агротехнических мероприятий на вариацию видов растительности. Однако выполненные парные сравнения выявили значимые отличия только для метода NM (оставить луга в естественном состоянии) от биологического BF или рекреационного HF вмешательства. Относительные расстояния между центроидами групп можно приблизительно оценить по ординационной диаграмме (рис. 9.2).
Для выполнения множественных сравнений наиболее распространённым и рекомендуемым в литературе является тест Тьюки, использующий критерий “подлинной” значимости (Honestly Significant Difference, HSD). HSD оценивает наименьшую величину разности математических ожиданий в группах, которую можно считать значимой. Тест Тьюки-HSD реализуется в R для модели betadisper с использованием базовой функции TukeyHSD(). На рис. 9.3 представлены рассчитанные этой функцией одновременные 95%-ные доверительные интервалы разности между каждой парой групп. Поскольку этот интервал не включает 0 только для одной сравниваемой пары (NM–BF), то значимые различия в видовом составе растительности имеются лишь между этими группами.
# Тест Тьюки HSD и график доверительных интервалов
(mod.HSD <- TukeyHSD(mod))## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = distances ~ group, data = df)
##
## $group
## diff lwr upr p adj
## HF-BF 0.04968632 -0.166780227 0.26615286 0.9116492
## NM-BF 0.21678406 0.007191225 0.42637689 0.0413759
## SF-BF 0.13061809 -0.078974740 0.34021092 0.3167622
## NM-HF 0.16709774 -0.012386839 0.34658232 0.0726265
## SF-HF 0.08093177 -0.098552804 0.26041635 0.5819039
## SF-NM -0.08616596 -0.257297794 0.08496586 0.4938236plot(mod.HSD)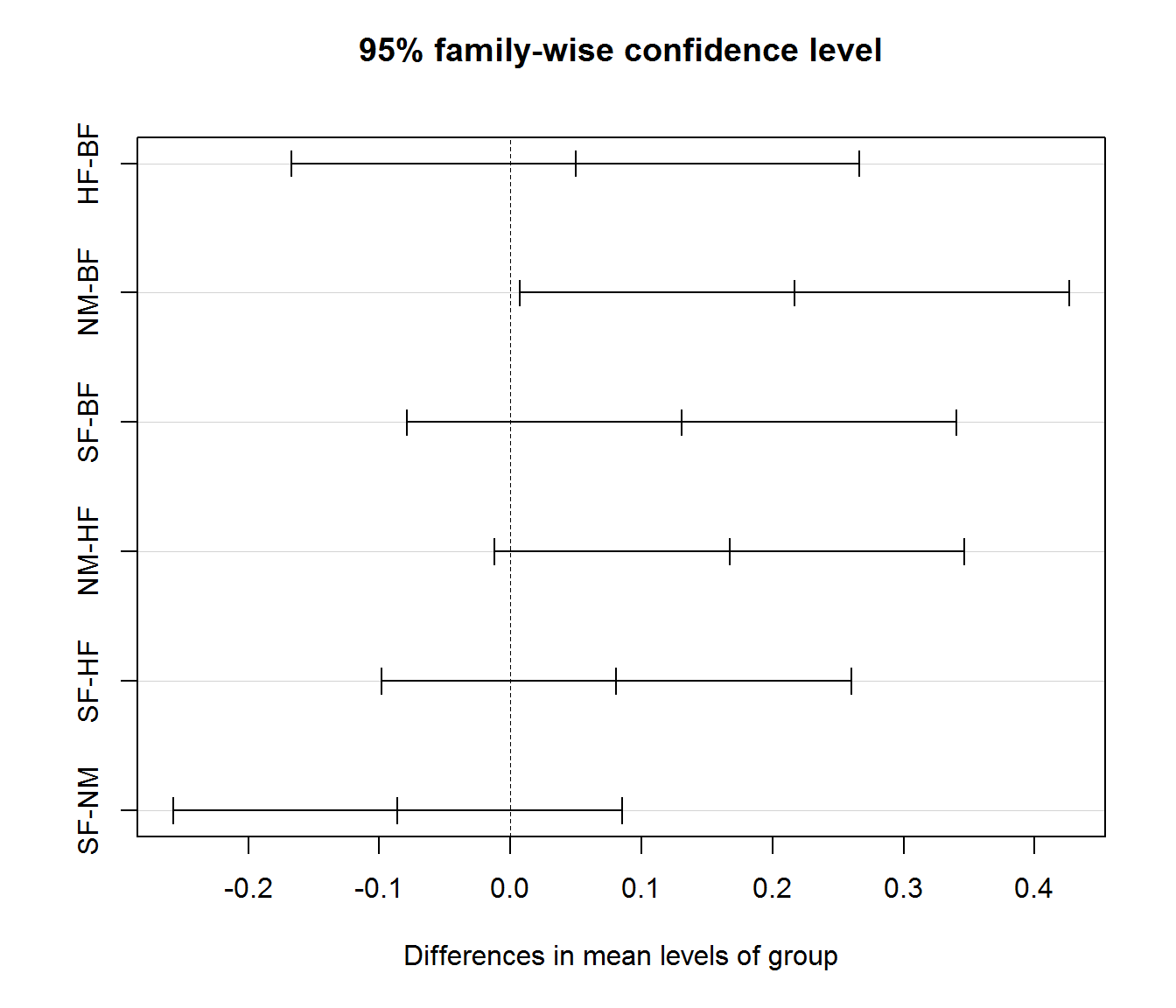
Рисунок 9.3: Множественные сравнения методов улучшения травостоя с использованием критерия HSD Тьюки