9.4 Оценка связи ординации с внешними факторами
Ранее мы рассматривали ординационный анализ только одной матрицы \(\mathbf{Y}\), чтобы получить отображение в ортогональной системе координат частных структурных особенностей изучаемой системы в форме графических проекций объектов и их признаков. Однако это - пассивный путь, поскольку он ограничивается фиксацией некоторого распределения точек на плоскости и не дает никаких объяснений этому феномену. Такую ординацию называют также непрямой, или неограниченной (unconstrained), в отличие от прямой, или ограниченной (constrained) ординации, которая ставит задачу связать внутреннюю изменчивость матрицы \(\mathbf{Y}\) с теми или иными внешними воздействиями \(\mathbf{X}\). Нам кажется, что непосредственный перевод приведенных терминов не вполне отражает суть дела и было бы точнее назвать эти методы ординации “необъясняющим” и “объясняющим” соответственно.
Концептуально канонический анализ позиционируется как расширение регрессионного анализа при моделировании многомерного отклика данных:
\[\mathbf{Y} = f(\mathbf{X}),\]
где матрица размером \(m \times n\) содержит значения отклика \(y_{ij}\), измеренные по \(m\) признакам (столбцы) для \(n\) объектов (строки); матрица размером \(n \times q\), в которой \(i\)-я строка содержит значения объясняющих переменных \(x_{ik}\).
Наиболее часто используются две математические процедуры канонической ординации, известные под аббревиатурами RDA и CCA. В обоих случаях формой канонизации является вычисление собственных чисел и собственных векторов.
Анализ избыточности (RDA, redundancy analysis; Rao, 1964; Legendre, Legendre, 2012), общий формализм и алгебра которого были описаны в разделе 2.5, является расширенной канонической формой, объединяющей линейную модель множественной регрессии и метод главных компонент РСА. Канонический анализ соответствий (CCA, canonical correspondence analysis; ter Braak, 1986) является модификацией RDA, выполняющей “взвешивание” ординационных компонент пропорционально их вкладу в статистику \(\chi^2\) , которая оценивает расстояния между объектами в многомерном пространстве. В связи с этим ССА в экологических приложениях придает существенно большее значение редко встречающимся видам, чем это делает RDA, основанный на евклидовых дистанциях.
В целом, оба метода - RDA и CCA - осуществляют аппроксимацию данных многомерной гауссовой регрессией и выполняют подгонку таких коэффициентов \(\mathbf{a} = (a_i)\) для переменных матрицы \(\mathbf{Y}\), \(i = 1, \dots, m\), и \(\mathbf{c} = (c_k)\) для факторов среды \(\mathbf{X}\), \(k = 1, \dots, q\), которые делают максимальной корреляцию между \(\mathbf{z^* = Y'a}\) и \(\mathbf{z = X'c}\). Расчеты в среде R обычно проводят с помощью функций rda() или cca() из пакета vegan. С этими функциями связано еще не менее двух десятков сервисных функций, выполняющих вычисление различных статистик, проверку гипотез о значимости как внутренних взаимодействий, так и о влиянии внешних факторов, и т.д.
Рассмотрим еще один геоботанический пример – набор ёvarespecё, описывающий относительное обилие 44 видов травянистых растений на 24 пробных площадках. Параллельный набор varechem содержит данные о 14 показателях химического состава почвы на тех же площадках.
Оценим предварительно характер распределения частот встречаемости объектов по рангам \(r\) списка видов \(S\). Осуществим аппроксимацию данных моделью Ципфа \(N_r = N p_1 r^{\gamma}\) с двумя оцениваемыми параметрами: \(p_1\) - долей самого многочисленного класса в общей численности \(N\) и \(\gamma\) - коэффициентом затухания гиперболической зависимости. Правда, мы имеем дело не с числом экземпляров растений, а с проективным покрытием в %, но не нет никакой сложности превратить формально непрерывные значения обилия в ряд положительных целочисленных величин:
library(vegan)
data(varechem)
data(varespec)
B <- rev(sort(colSums(varespec)))
BF <- as.matrix(t(round(B/min(B))))
rad <- rad.zipf(BF)
barplot(BF)
lines(1:ncol(BF), rad$fitted, col = "green", lwd = 2)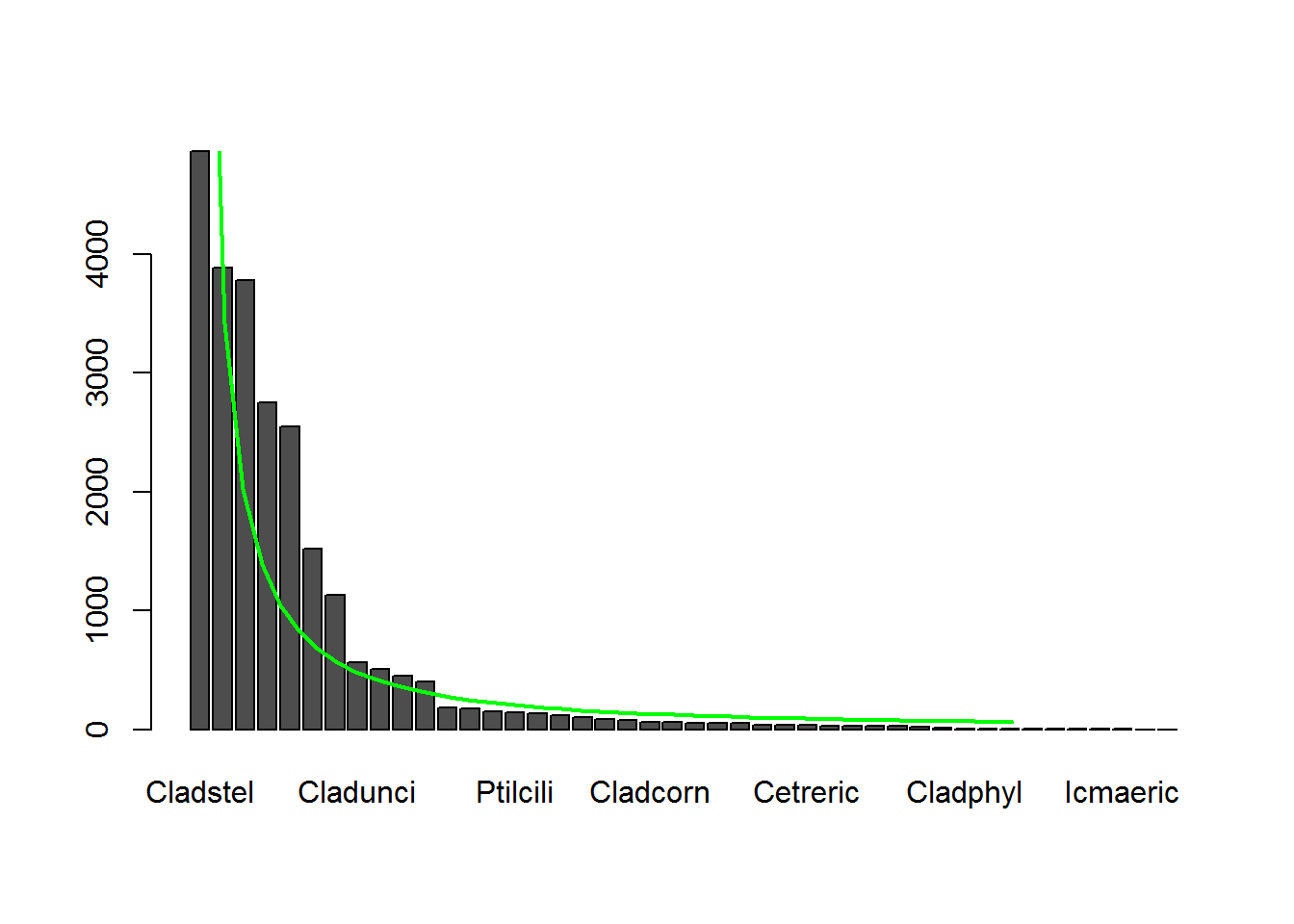
Рисунок 9.11: Аппроксимация рангового распределения видов моделью Ципфа
Поскольку полученное распределение имеет очевидную склонность к доминированию, подвергнем анализируемые данные \(\chi^2\)-преобразованию. Оценим влияние отдельных химических элементов в почве на встречаемость видов с использованием канонического анализа соответствий CCA (рис. 9.12):
varespec.chi <- decostand(varespec, method = "chi.square")
mod1.cca <- cca(varespec.chi ~ ., varechem)
spec <- as.data.frame(mod1.cca$CCA$v[, 1:2]) # Виды
sites <- as.data.frame(mod1.cca$CCA$u[, 1:2]) # Площадки
fact <- as.data.frame(mod1.cca$CCA$biplot[, 1:2]) # Факторы
library(ggplot2)
ggplot() +
geom_point(data = sites, aes(x = CCA1, y = CCA2), size = 3,
shape = 17, color = "red") + # добавляем точки площадок
geom_text(data = spec, aes(x = CCA1, y = CCA2,
label = abbreviate(rownames(spec), 4)),
colour = "darkgreen", fontface = 3) + # добавляем метки видов
geom_segment(data = fact, aes(x = 0, xend = CCA1, y = 0, yend = CCA2),
arrow = arrow(length = unit(0.3, "cm")),
colour = "darkblue") + # добавляем стрелки факторов
geom_text(data = fact, aes(x = CCA1, y = CCA2,
label = rownames(fact), size = 6),
hjust = 1.2, fontface = 2) + theme_bw() +
theme(legend.position = "NA")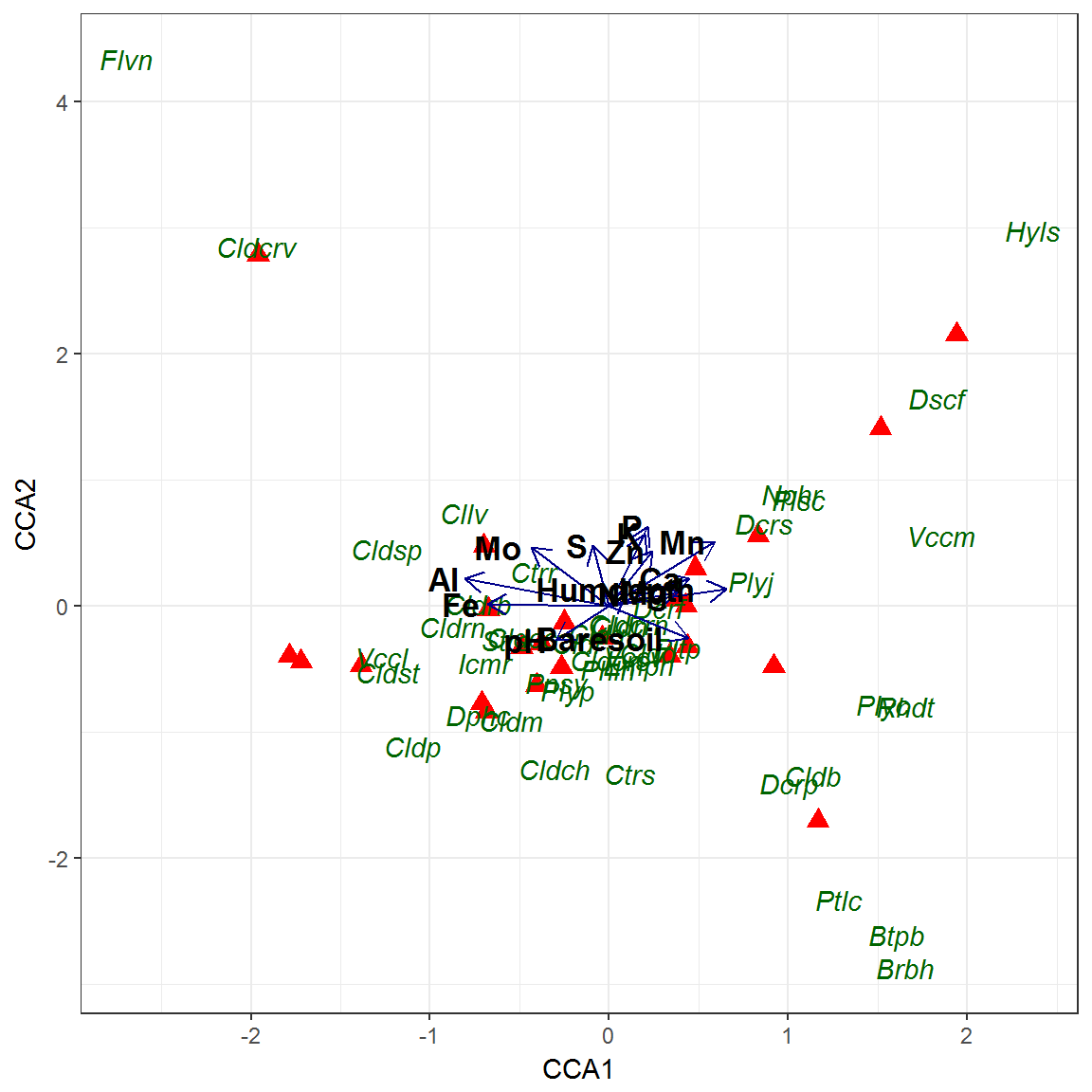
Рисунок 9.12: Ординационный триплот, полученный методом CCA
Из результатов следует, что всего было сформировано 23 (т.е. \(n-1\)) линейно независимых оси ординации, в том числе 14 осей объясняющих переменных (Constrained). 69% совокупной многомерной дисперсии (Inertia) матрицы связаны с химическим составом почвы, а 31% - со случайными или неучтенными факторами . Результирующая диаграмма (“триплот”, см. рис. 9.12) отражает не только изменчивость видового состава относительно двух осей проецирования CCA1-CCA2, но и статистические связи между видами и каждой независимой переменной \(x_{ji}\). Для этого из центра координат стрелками синего цвета проведены дополнительные оси (constrained axes), ориентация которых зависит от значений канонических собственных векторов. Относительная длина стрелки пропорциональна силе связи внешнего фактора с осями ординации CCA1-CCA2, а косинус угла между каждой парой стрелок приблизительно равен коэффициенту их корреляции (положительной или отрицательной).
Как и в случае биплота, координаты каждого вида находятся вблизи точек тех площадок, где его обилие наиболее высоко. Если виды представить стрелками, исходящими из начала координат, то косинус угла между стрелкой соответствующего вида и стрелкой фактора среды приблизительно равен коэффициенту корреляции между ними. Например, обилие вида Callvulg (Cllv) в значительной степени коррелирует с содержанием в почве молибдена, в отличие от Cladphyl (Cldp). Проекция точки вида на каждую стрелку показывает его экологический оптимум (точнее, центр тяжести распределения обилия) относительно этого химического компонента.
Нетрудно убедиться, что показатели состава почвы очень высоко коррелирут друг с другом, о чем свидетельствует фактор инфляции дисперсии VIF.
library(car)
sort(vif(mod1.cca))## N Baresoil Mn Humdepth Mo P pH
## 1.637648 1.966942 5.163652 5.258233 5.760964 6.398181 6.593768
## Zn Fe Ca Mg K S Al
## 8.446984 9.100191 9.295130 10.531890 11.705305 20.424393 21.546563paste("AIC=", extractAIC(mod1.cca)[2])## [1] "AIC= 65.5835241860133"Дисперсионный анализ anova() в отношении объектов ССА или RDA имеет важный параметр by: при by = "axis" оценивается значимость объясняющих осей, значение by = "term" дает возможность последовательно проверить по \(F\)- и \(\chi^2\)-критериям значимость отдельных коэффициентов регрессионной модели, а в случае by = "margin" проверяется наличие маргинального эффекта. Если параметр by не задан, то оценивается значимость ординационной модели в целом. Естественно, что все проверки осуществляются с использованием перестановочного теста, т.е. проводится многократное случайное перемешивание строк исходных таблиц и оценивается независимость результатов проверки нулевой гипотезы от процесса хаотического обмена (exchangeability) анализируемых единиц.
Высокая мультиколлинеарность таблицы \(\mathbf{X}\) обусловливает низкую статистическую значимость включения в линейную модель почти каждой из объясняющих переменных:
anova(mod1.cca)## Permutation test for cca under reduced model
## Permutation: free
## Number of permutations: 999
##
## Model: cca(formula = varespec.chi ~ N + P + K + Ca + Mg + S + Al + Fe + Mn + Zn + Mo + Baresoil + Humdepth + pH, data = varechem)
## Df ChiSquare F Pr(>F)
## Model 14 2.2603 1.4304 0.064 .
## Residual 9 1.0158
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(mod1.cca, by = "term", step = 200)## Permutation test for cca under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
##
## Model: cca(formula = varespec.chi ~ N + P + K + Ca + Mg + S + Al + Fe + Mn + Zn + Mo + Baresoil + Humdepth + pH, data = varechem)
## Df ChiSquare F Pr(>F)
## N 1 0.16487 1.4607 0.216
## P 1 0.23009 2.0385 0.023 *
## K 1 0.22026 1.9514 0.121
## Ca 1 0.17213 1.5250 0.216
## Mg 1 0.11727 1.0390 0.544
## S 1 0.23605 2.0913 0.017 *
## Al 1 0.17953 1.5906 0.126
## Fe 1 0.11987 1.0620 0.499
## Mn 1 0.13858 1.2278 0.355
## Zn 1 0.14076 1.2470 0.304
## Mo 1 0.13971 1.2377 0.318
## Baresoil 1 0.14812 1.3123 0.268
## Humdepth 1 0.12972 1.1493 0.380
## pH 1 0.12330 1.0924 0.423
## Residual 9 1.01585
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Для построения оптимальной модели выполним алгоритм пошагового включения переменных, стартуя от нуль-модели mod0.cca. На каждом шаге будем проводить перестановочный тест значимости включаемого члена:
mod0.cca <- cca(varespec.chi ~ 1, varechem)
set.seed(1)
mod.cca <- step(mod0.cca, scope = formula(mod1.cca),
test = "perm", trace = 0)
mod.cca$anova## Step Df Deviance Resid. Df Resid. Dev AIC
## 1 NA NA 23 340.9154 65.68593
## 2 + Al -1 37.46399 22 303.4514 64.89202
## 3 + P -1 25.64418 21 277.8072 64.77296
## 4 + K -1 24.38595 20 253.4212 64.56798anova(mod.cca)## Permutation test for cca under reduced model
## Permutation: free
## Number of permutations: 999
##
## Model: cca(formula = varespec.chi ~ Al + P + K, data = varechem)
## Df ChiSquare F Pr(>F)
## Model 3 0.8408 2.3017 0.001 ***
## Residual 20 2.4353
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(mod.cca, by = "axis")## Permutation test for cca under reduced model
## Marginal tests for axes
## Permutation: free
## Number of permutations: 999
##
## Model: cca(formula = varespec.chi ~ Al + P + K, data = varechem)
## Df ChiSquare F Pr(>F)
## CCA1 1 0.38691 3.1775 0.001 ***
## CCA2 1 0.24503 2.0123 0.014 *
## CCA3 1 0.20886 1.7153 0.093 .
## Residual 20 2.43532
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1При выполнении пошаговой процедуры уже после 4-го шага началось увеличение AIC-критерия при полном составе переменных. В итоге была получена модель с высокой степенью статистической значимости в целом, однако использование уже третьей факторной оси, возможно, оказалось излишним. Судя по всему, алгоритм не смог разумно распорядиться высокой корреляционной зависимостью между содержанием фосфора и калия (см. рис. 9.11).