6.5 Процедуры сравнения эффективности моделей классификации
Итак, мы использовали шесть методов для построения моделей бинарной классификации. Осуществим их сравнение для данного примера с полным сохранением всех канонов тестирования моделей прогнозирования (Kuhn, Johnson, 2013) и в соответствии с методикой, представленной в сообщении http://machinelearningmastery.com:
- Проводим разделение имеющейся выборки на обучающую и проверочную (использование фактора в качестве аргумента функции
createDataPartition()обеспечивает необходимый баланс его уровней при разделении). Для обучения выделим 70% (115 элементов) исходной выборки:
set.seed(7)
train <- unlist(createDataPartition(DGlass$FAC, p = 0.7))
# определение схемы тестирования
control <- trainControl(method = "repeatedcv",
number = 10, repeats = 3, classProbs = TRUE)- Выполняем обучение шести моделей:
# LDA - линейный дискриминантный анализ
set.seed(7)
fit.lda <- train(DGlass[train, 3:4], DGlass$FAC[train],
method = "lda", trControl = control)
# SVML - метод опорных векторов с линейным ядром
set.seed(7)
fit.svL <- train(DGlass[train, 1:9], DGlass$FAC[train],
method = "svmLinear", trControl = control)
# SVMR - метод опорных векторов с радиальным ядром
set.seed(7)
fit.svR <- train(DGlass[train, 1:9], DGlass$FAC[train],
method = "svmRadial", trControl = control,
tuneGrid = expand.grid(sigma = 0.4, C = 2))
# CART - дерево классификации
set.seed(7)
fit.cart <- train(DGlass[train, 1:9], DGlass$FAC[train],
method = "rpart", trControl = control)
# RF - случайный лес
set.seed(7)
fit.rf <- train(DGlass[train, 1:9], DGlass$FAC[train],
method = "rf", trControl = control)
# GLM - Логистическая регрессия
set.seed(7)
fit.glm <- train(DGlass[train, -c(1, 4, 10, 11)],DGlass$FAC[train],
method = "glm", family = binomial, trControl = control)- Осуществляем ресэмплинг полученных моделей, выполняем статистический анализ двух сформированных метрик качества моделей (
Accuracyи индексKappaДж. Коэна) на обучающей выборке, ранжируем модели и оцениваем доверительные интервалы использованных критериев:
caret.models <- list(LDA = fit.lda, SVML = fit.svL,
SVMR = fit.svR, CART = fit.cart,
RF = fit.rf, GLM = fit.glm)
# ресэмплинг коллекции моделей
results <- resamples(caret.models)
# обобщение различий между моделями
summary(results)##
## Call:
## summary.resamples(object = results)
##
## Models: LDA, SVML, SVMR, CART, RF, GLM
## Number of resamples: 30
##
## Accuracy
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## LDA 0.5455 0.6667 0.7937 0.7787 0.9091 1.0000 0
## SVML 0.5000 0.6364 0.7273 0.7135 0.8011 0.9167 0
## SVMR 0.6364 0.7273 0.8182 0.8081 0.8934 1.0000 0
## CART 0.5455 0.7330 0.8333 0.8195 0.9091 1.0000 0
## RF 0.6364 0.8182 0.8776 0.8728 1.0000 1.0000 0
## GLM 0.5000 0.6667 0.7273 0.7251 0.8182 0.9167 0
##
## Kappa
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## LDA 0.0678 0.3333 0.5754 0.5502 0.8181 1.0000 0
## SVML 0.0000 0.2477 0.4391 0.4181 0.5905 0.8333 0
## SVMR 0.2667 0.4590 0.6270 0.6141 0.7828 1.0000 0
## CART 0.0678 0.4821 0.6667 0.6366 0.8197 1.0000 0
## RF 0.2667 0.6239 0.7482 0.7443 1.0000 1.0000 0
## GLM 0.0000 0.3333 0.4590 0.4459 0.6333 0.8333 0# Оценка доверительных интервалов и построение графика
scales <- list(x = list(relation = "free"),
y = list(relation = "free"))
dotplot.resamples(results)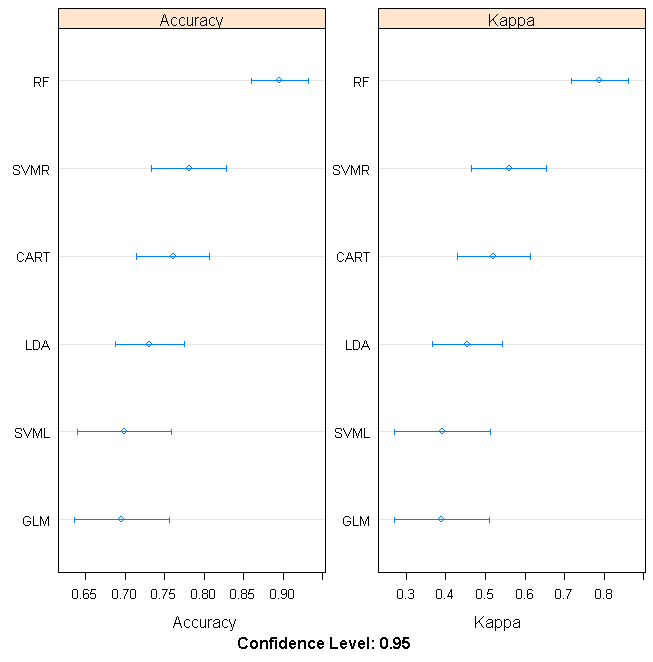
Рисунок 6.8: Сравнительный статистический анализ двух метрик эффективности шести моделей прогнозирования типа стекла
- Наконец, можно вычислить статистическую значимость различий между моделями на основе распределения оценок критериев качества. Для этого воспользуемся функцией
diff():
diffs <- diff(results)
# summarize p-values for pair-wise comparisons
summary(diffs)##
## Call:
## summary.diff.resamples(object = diffs)
##
## p-value adjustment: bonferroni
## Upper diagonal: estimates of the difference
## Lower diagonal: p-value for H0: difference = 0
##
## Accuracy
## LDA SVML SVMR CART RF GLM
## LDA 0.06519 -0.02937 -0.04073 -0.09406 0.05361
## SVML 0.0058827 -0.09456 -0.10592 -0.15925 -0.01158
## SVMR 1.0000000 0.0013835 -0.01136 -0.06469 0.08298
## CART 0.4810803 2.101e-05 1.0000000 -0.05332 0.09435
## RF 5.290e-05 1.169e-09 0.0708208 0.0891429 0.14767
## GLM 0.1042965 1.0000000 0.0032517 0.0007246 1.971e-09
##
## Kappa
## LDA SVML SVMR CART RF GLM
## LDA 0.13215 -0.06383 -0.08632 -0.19409 0.10437
## SVML 0.0070527 -0.19599 -0.21847 -0.32624 -0.02778
## SVMR 1.0000000 0.0007739 -0.02248 -0.13025 0.16821
## CART 0.3928054 1.583e-05 1.0000000 -0.10777 0.19069
## RF 4.549e-05 5.371e-10 0.0654607 0.0951760 0.29846
## GLM 0.1556033 1.0000000 0.0029324 0.0008886 1.784e-09Результаты выше главной диагонали таблицы статистической значимости содержат разности между центрами распределения. Эти значения показывают, как модели соотносятся друг с другом по абсолютному значению точности. Данные ниже диагонали таблицы представляют собой \(p\)-значения для нулевой гипотезы, которая утверждает, что параметры распределения одинаковы. Например, очевидно, что модель Random Forrest статистически значимо точнее всех остальных.
- Составим таблицу прогноза всеми шестью моделями для 48 проверочных наблюдений:
pred.fm <- data.frame(
LDA = predict(fit.lda, DGlass[-train, 3:4]),
SVML = predict(fit.svL, DGlass[-train, 1:9]),
SVMR = predict(fit.svR, DGlass[-train, 1:9]),
CART = predict(fit.cart, DGlass[-train, 1:9]),
RF = predict(fit.rf, DGlass[-train, 1:9]),
GLM = predict(fit.glm, DGlass[-train,-c(1, 4, 10, 11)])
)Резерв повышения надежности моделей прогнозирования многими исследователями видится в объединении отдельных моделей в “ансамбль” (ensemble) и построении системы коллективного распознавания. Простейшим способом комбинирования результатов бинарной классификации является выбор класса, за который “проголосовало” большинство предсказывающих моделей. Добавим в таблицу прогнозов столбец с результатами голосования (методу Random Forrest, как наиболее эффективному, отдано два голоса):
CombyPred <- apply(pred.fm, 1, function (voice) {
voice2 <- c(voice, voice[5]) # У RF двойной голос
ifelse(sum(voice2 == "Flash") > 3, "Flash", "No") }
)
pred.fm <- cbind(pred.fm, COMB = CombyPred)
head(pred.fm)## LDA SVML SVMR CART RF GLM COMB
## 1 Flash No No Flash No No No
## 2 No No No No No No No
## 3 Flash No Flash Flash Flash No Flash
## 4 Flash Flash Flash Flash Flash Flash Flash
## 5 Flash Flash Flash Flash Flash Flash Flash
## 6 Flash Flash Flash Flash Flash Flash Flash- Определимся со списком критериев, которые следует использовать для тестирования. Кроме традиционных оценок точности
AC, чувствительностиSEи специфичностиSP, воспользуемся дополнительными метриками, рекомендованными в обзоре http://datareview.info и позволяющими получить несмещенную оценку, особенно в случае несбалансированных классов:F-мера (\(F\)-score)= 2 * AC * SE / (AC + SE)и коэффициент корреляции Мэтьюса (Matthews сorrelation сoefficient, MCC):
\[MCC = \frac{(TP \times TN) - (FP \times FN)}{\sqrt{(TP+FP)\times(TP+FN)\times(TN+FP)\times(TN+FN)}}\]
(условные обозначения см. в разделе 2.3).
# Функция формирования строки критериев
ModCrit <- function(fact, pred) {
cM <- table(fact, pred)
c( Accur <- (cM[1, 1] + cM[2, 2])/sum(cM),
Sens <- cM[1, 1]/(cM[1, 1] + cM[2, 1]),
Spec <- cM[2, 2]/(cM[2, 2] + cM[1, 2]),
F.score <- 2 * Accur * Sens / (Accur + Sens),
MCC <- ((cM[1, 1]*cM[2, 2]) - (cM[1, 2]*cM[2, 1])) /
sqrt((cM[1, 1] + cM[1, 2])*(cM[1, 1] + cM[2, 1]) *
(cM[2, 2] + cM[1, 2])*(cM[2, 2] + cM[2, 1])) )
}
Result <- t(apply(pred.fm, 2, function(x) ModCrit(DGlass$FAC[-train], x)))
colnames(Result) <- c("Точность", "Чувствит.", "Специфичн.", "F-мера", "КК Мэтьюса")
round(Result, 3)## Точность Чувствит. Специфичн. F-мера КК Мэтьюса
## LDA 0.688 0.704 0.667 0.696 0.369
## SVML 0.562 0.600 0.522 0.581 0.122
## SVMR 0.792 0.786 0.800 0.789 0.580
## CART 0.708 0.714 0.700 0.711 0.410
## RF 0.750 0.769 0.727 0.759 0.497
## GLM 0.542 0.571 0.500 0.556 0.071
## COMB 0.688 0.690 0.684 0.689 0.367По существу проведенных расчетов можно сделать два вывода:
- при тестировании на “свежих” данных модель Random Forrest уступает по эффективности модели опорных векторов с радиальным ядром;
- прогноз “голосующего коллектива” COMB имеет умеренные показатели точности предсказания на фоне индивидуальных моделей.
В разделе 2.3 было показано, что универсальным способом сравнения точности классификаторов является ROC-анализ. Воспользовавшись тем, что при обучении мы сохранили вероятности принадлежности к классам (classProbs = TRUE), построим ROC-кривые для трех используемых методов распознавания (LDA, SVMR и RF) по полной таблице исходных данных, включая обучающую и тестовую последовательности. Будем анализировать вероятности отнесения к классу Flash, т.е. 1-й столбец таблицы вероятностей, возвращаемой функцией predict() при значении параметра type = "prob":
# Извлекаем вероятности классов по всей выборке
pred.lda.roc <- predict(fit.lda, DGlass[, 3:4], type = "prob")
pred.svmR.roc <- predict(fit.svR, DGlass[, 1:9], type = "prob")
pred.rf.roc <- predict(fit.rf, DGlass[, 1:9], type = "prob")
library(pROC) # Строим три ROC-кривые
m1.roc <- roc(DGlass$FAC, pred.lda.roc[, 1])
m2.roc <- roc(DGlass$FAC, pred.svmR.roc[, 1])
m3.roc <- roc(DGlass$FAC, pred.rf.roc[, 1])plot(m1.roc, grid.col = c("green", "red"), grid = c(0.1, 0.2),
print.auc = TRUE, print.thres = TRUE)
plot(m2.roc , add = TRUE, col = "green", print.auc = TRUE,
print.auc.y = 0.45, print.thres = TRUE)
plot(m3.roc , add = TRUE, col = "blue", print.auc = TRUE,
print.auc.y = 0.40,print.thres = TRUE)
legend("bottomright", c("LDA","SVM","RF","COMBY"), lwd = 2,
col = c("black", "green", "blue", "red"))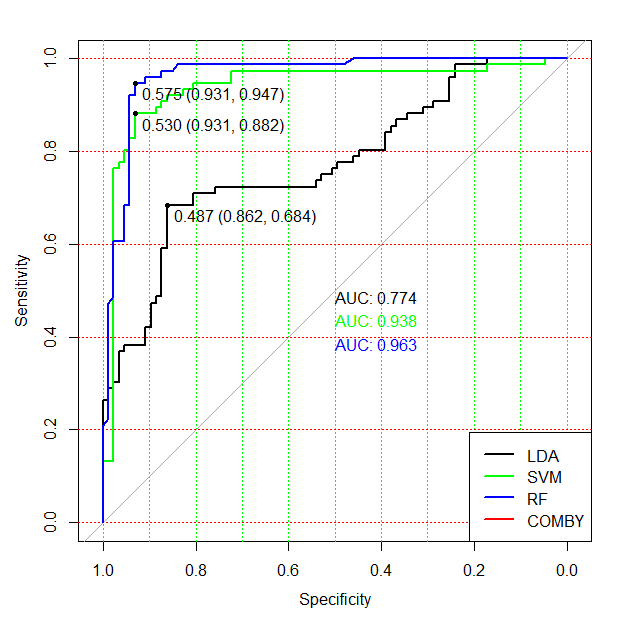
Рисунок 6.9: ROC-кривые для четырех моделей классификации
Нетрудно заметить, что каждая модель, в силу характерных для нее стратегий распознавания, имеет различную эффективность классификации на каждом из диапазонов значений апостериорных вероятностей \(p\) класса Flash. Например, классификатор SVM на опорных векторах имеет определенное преимущество при предсказании объектов в критической зоне разделения (между \(p = 0.4\) и \(p = 0.6\)) и при пороговом значении \(p = 0.53\) он достигает максимальной точности (чувствительность SE = 93.1% и специфичность SP = 88.2%). В других диапазонах \(p\) эффективность модели SVM несколько уступает остальным классификаторам, что имеет свои объяснения, если вспомнить механизм распознавания на основе опорных векторов.
Максимум значения AUC на рис. 6.9 принадлежит модели случайного леса, но использование функций ci.auc() и roc.test() даст нам доверительные интервалы для AUC и позволит сделать вывод о значимости различий между классификаторами по этому показателю.
# Доверительные интервалы для параметров ROC-анализа:
ci.auc(m2.roc)## 95% CI: 0.8949-0.9814 (DeLong)ci.auc(m3.roc)## 95% CI: 0.9344-0.9919 (DeLong)roc.test(m2.roc, m3.roc)##
## DeLong's test for two correlated ROC curves
##
## data: m2.roc and m3.roc
## Z = 1.5878, p-value = 0.1123
## alternative hypothesis: true difference in AUC is not equal to 0
## sample estimates:
## AUC of roc1 AUC of roc2
## 0.9381428 0.9631730Результаты свидетельствуют, что по величине AUC метод случайного леса (m3.roc) на полной выборке значимо превосходит метод опорных векторов (m2.roc). Аналогичные функции ci.se() и ci.sp() дадут возможность сделать такой же вывод относительно чувствительности и специфичности.
Вернемся к нашим попыткам осуществить коллективный прогноз. Кроме голосования моделей, вторым простым способом комбинирования результатов бинарной классификации является расчет взвешенной средней апостериорной вероятности отнесения объекта к тому или иному классу \(p_c = \sum_j w_j p_j\), где \(p_j\) - частные вероятности, полученные g различными классификаторами, \(w_j\) - веса, нормирующие “компетентность” отдельных моделей. В качестве весов могут использоваться оценки экспертов или любые другие статистики (например, AUC, предварительно возведенную в квадрат для увеличения “контраста” и нормированную на их сумму по трем выбранным методам):
weight <- c(as.numeric(m1.roc$auc)^2,
as.numeric(m2.roc$auc)^2,
as.numeric(m3.roc$auc)^2)
weight <- weight/sum(weight)
Pred = data.frame(lda = pred.lda.roc[, 1],
svm = pred.svmR.roc[, 1],
rf = pred.rf.roc[, 1])
CombyPred <- apply(Pred, 1, function(x) sum(x*weight))Построим ROC-кривую для комбинированного прогноза по этому методу и добавим ее на рис. 6.9 - COMBY. С помощью функции coord() можно вывести полную информацию об оптимальной пороговой точке (threshold) полученного классификатора.
m.Comby <- roc(DGlass$FAC, CombyPred)
plot(m.Comby, add = TRUE, col = "red",
print.auc = TRUE, print.auc.y = 0.35)
coords(m.Comby, "best", ret = c("threshold", "specificity",
"sensitivity", "accuracy"))