7.6 Классификаторы на основе искусственных нейронных сетей
Нейросетевые модели, родившиеся в процессе развития концепции искусственного интеллекта, имеют две вполне прозрачные аналогии - биологическая нейронная система мозга и компьютерная сеть. Их основная парадигма состоит в том, что решение в сети формируется множеством простых нейроноподобных элементов, образующих граф с взвешенными синаптическими (информационными) связями, которые совместно и целенаправленно работают на получение общего результата. Таким образом, искусственная нейронная сеть (ИНС) является (Дук, Самойленко, 2001):
- параллельной системой, поскольку в любой момент времени в активном состоянии могут находиться несколько процессов;
- распределенной системой, поскольку каждый из процессов может независимо обрабатывать локальные данные;
- адаптивной системой, наделенной свойствами самообучения и подстройки своих параметров при изменении профиля данных.
Главным строительным блоком ИНС является формальный нейрон, структура которого имеет вид, представленный на рис. 7.10:
Рисунок 7.10: Структура искусственного нейрона (слева) и вид некоторых функций активации (справа); обозначения по тексту
Основная функция искусственного нейрона - cформировать выходной сигнал \(y\) в зависимости от сигналов \(x_1, \dots, x_n\), поступающих на его входы. Эти значения могут усиливаться или “тормозиться” в зависимости от знака весов синапсов \(w_1, \dots, w_n\). Входные сигналы обрабатываются адаптивным сумматором \(\sum_{i=1}^n w_i x_i -T\), где \(T\) - порог нейрона, а затем выходной сигнал сумматора поступает в нелинейный преобразователь \(\mathbf{F}\) с некоторой функцией активации, после чего результат подается на выход (в точку ветвления).
Вид функции активации может иметь различное математическое выражение, выбор которого определяется характером решаемых задач. Например, преобразование может осуществляться функцией, определенной как единичный скачок (а на рис. 7.10, линейный порог (гистерезис, б), гиперболический тангенс (в) или сигмоид (г). Наиболее распространена нелинейная функция с насыщением - так называемая логистическая функция, или сигмоид - \(y = \frac{1}{1 + e^{-cS}}\), которая имеет много ценных свойств (монотонность и дифференцируемость, устойчивость к выбросам, простое выражение для ее производной и т.д.). Выходное значение сигмоидального нейрона лежит в диапазоне [0, 1]. При уменьшении коэффициента с сигмоид становится более пологим, вырождаясь в пределе при \(c = 0\) в горизонтальную линию на уровне 0.5. При увеличении с сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке \(x = 0\).
По способу соединения нейронов выделяют сети с разной архитектурой: персептроны, сети адаптивного резонанса, рециркуляционные, рекуррентные, встречного распространения, ИНС с обратными связями Хэмминга и Хопфилда, с двунаправленной ассоциативной памятью, с радиально-базисной функцией активации, самоорганизующиеся ИНС Кохонена и т.п. Мы будем рассматривать возможности обучения ИНС на примере многослойного персептрона с прямым распространением информации, структура которого представлена на рис. 7.11.
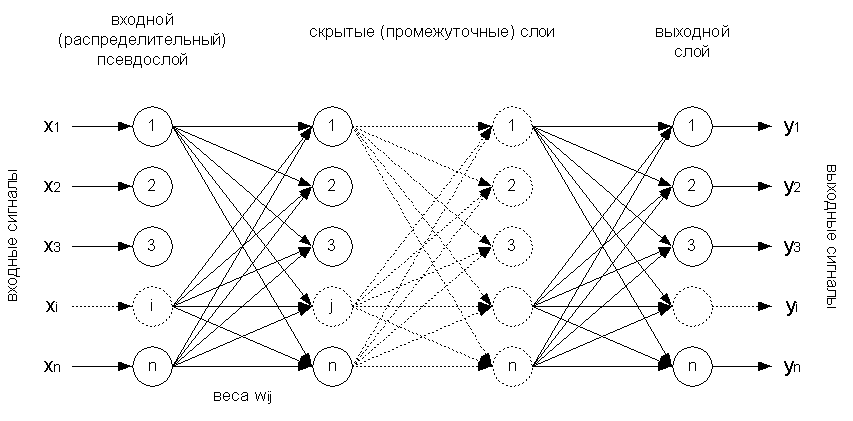
Рисунок 7.11: Структура многослойного персептрона
Нейроны персептрона регулярным образом организованы в слои, причем информация направленно распространяется от предыдущих слоев к последующим. Входной слой состоит из n нейронов, на которые подаются значения исходных переменных \(X_i\), никакой обработки информации не совершает и выполняет лишь распределительные функции. Если сеть настроена на классификацию, то взвешенные комбинации \(y\) выходного слоя представляют собой прогноз, указывающий на принадлежность распознаваемого объекта к определенной группе. Если распознаются только два класса, то в выходном слое персептрона находится только один элемент, который обладает двумя реакциями - положительной и отрицательной. Если классов больше двух, то для каждой группы устанавливается свой нейрон, и тогда выход \(y_k\) каждого такого элемента представляет нелинейную комбинацию его входов, аккумулировавших результаты работы всех предыдущих слоев.
Двухслойный персептрон Розенблата, в принципе, аналогичен логистической регрессии, но добавление произвольного числа промежуточных (скрытых) слоев позволяет существенно усложнить структуру модели и реализовать различные множественные связи нейронов друг с другом с помощью последовательного взятия их линейных комбинаций и применения нелинейных функций активации \(f\) (Ripley, 1995):
\[ y_k = f_0 \left( \sum_{i \rightarrow k} w_{ik} x_i + \sum_{j \rightarrow k} w_{jk} f_h \left( \sum_{i \rightarrow k} w_{ik} x_i \right) \right).\]
В многослойной сети такие функции отклика дают возможность практически точно аппроксимировать любые выпуклые многомерные функциональные зависимости. Настройка сети представляет достаточно сложную задачу: необходимо подобрать количество промежуточных слоев и число нейронов в каждом из них, установить типы активационной функции и оценить коэффициенты \(w_i\), \(c_i\) каждого нейрона, которые бы минимизировали ошибку прогноза, выдаваемого сетью. Нахождение глобального оптимума аналитическими методами тут невозможно, но разработаны вполне эффективные методы исследования поверхностей ошибок и движения по градиенту. Выбор нейросети “правильной” сложности, как и в рассмотренных ранее случаях, сводится к двум рецептам: использование контрольных выборок и экспериментирование.
Для обучения ИНС в среде R используются два пакета - neuralnet и nnet, - обеспечивающие гибкие функциональные возможности построения моделей классификации и регрессии на основе многослойного персептрона. Вернемся снова к данным по ирисам Фишера и разделим ее на обучающую и тестовую выборки в соотношении 7:3, а также добавим в исходную таблицу три столбца, содержащих значения TRUE/FALSE для каждого вида растений:
data(iris)
set.seed(101)
ind <- sample(2, nrow(iris), replace = TRUE, prob = c(0.7, 0.3))
trainset <- iris[ind == 1, ]
testset <- iris[ind == 2, ]
trainset$setosa <- trainset$Species == "setosa"
trainset$virginica <- trainset$Species == "virginica"
trainset$versicolor <- trainset$Species == "versicolor"Построим сеть с тремя слоями, содержащими три нейрона в скрытом слое:
library(neuralnet)
set.seed(1)
net.iris <- neuralnet(versicolor + virginica + setosa ~
Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
trainset, hidden = 3)
net.iris$result.matrix## 1
## error 0.474288699703
## reached.threshold 0.009999089349
## steps 41578.000000000000
## Intercept.to.1layhid1 3.341946189258
## Sepal.Length.to.1layhid1 4.152043324222
## Sepal.Width.to.1layhid1 3.132771387590
## Petal.Length.to.1layhid1 5.232080802138
## Petal.Width.to.1layhid1 3.966307771815
## Intercept.to.1layhid2 80.876034918730
## Sepal.Length.to.1layhid2 6.982633187582
## Sepal.Width.to.1layhid2 10.324852382161
## Petal.Length.to.1layhid2 -23.484913875392
## Petal.Width.to.1layhid2 -23.219033469824
## Intercept.to.1layhid3 -7.519141407549
## Sepal.Length.to.1layhid3 2.576521564536
## Sepal.Width.to.1layhid3 2.901439191047
## Petal.Length.to.1layhid3 -2.900196758676
## Petal.Width.to.1layhid3 -7.332671088032
## Intercept.to.versicolor -0.020880768370
## 1layhid.1.to.versicolor 0.007862577547
## 1layhid.2.to.versicolor 1.029881445988
## 1layhid.3.to.versicolor -1.017411740038
## Intercept.to.virginica 0.343895963982
## 1layhid.1.to.virginica 0.668972014373
## 1layhid.2.to.virginica -1.025238210107
## 1layhid.3.to.virginica 0.012422611868
## Intercept.to.setosa -1.304517670769
## 1layhid.1.to.setosa 1.304659772989
## 1layhid.2.to.setosa -0.004636444971
## 1layhid.3.to.setosa 1.004990455015Из сводки итоговых результатов видно, что процесс обучения нуждался в нескольких тысячах шагов (steps), пока максимумы всех частных производных функции ошибок reached.threshold по абсолютной величине не оказались ниже чем 0.01 (порог по умолчанию). Ошибка error оценивается как уровень правдоподобия по критерию AIC. Остальные величины, представленные в net.iris$result.matrix и net.iris$generalized.weights, содержат весовые коэффициенты \(w\) и значения сигмоид \(c\) для каждого нейрона, которые можно должным образом проанализировать и интерпретировать. Это легко сделать, получив изображение ИНС (рис. 7.12):
plot(net.iris)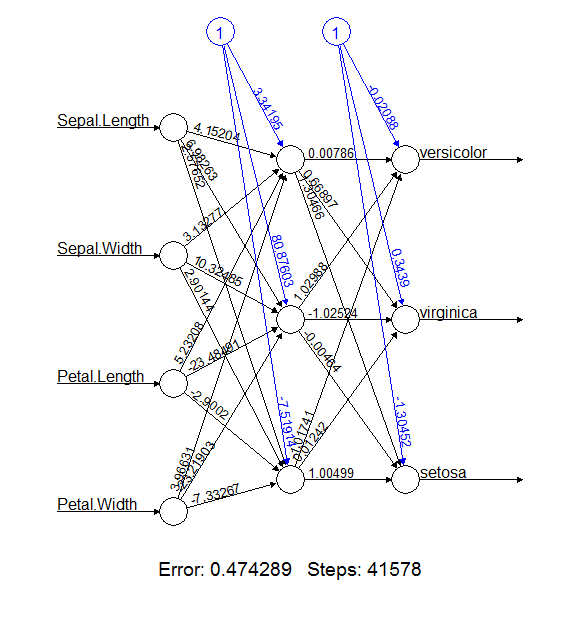
Рисунок 7.12: График обученной нейронной сети
На рис. 7.12 видно, что на выходной слой поступает 12 сигналов, которые представляют собой скомбинированные и трансформированные значения четырех исходных переменных. С их использованием и на основе обобщенных весов и функций активации последнего слоя оцениваются вероятности отнесения растения к каждому из трех видов. Для проверочной выборки процесс распознавания выглядит так:
net.prob <- compute(net.iris, testset[-5])$net.resultpred = c("versicolor", "virginica", "setosa")[apply(net.prob, 1, which.max)]
(table(Факт = testset$Species, Прогноз = pred))## Прогноз
## Факт setosa versicolor virginica
## setosa 16 0 0
## versicolor 0 19 1
## virginica 0 0 13Acc = mean(pred == testset$Species)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=97.96%"Дальнейшее рассмотрение особенностей нейросетевых моделей мы продолжим в следующей главе на более представительном примере.