4.5 Сравнение построенных моделей и оценка информативности предикторов

Разделы 4.1-4.4 содержат подробную информацию о результатах тестирования различных типов моделей регрессии в идентичных условиях и на одном и том же примере, обобщенную в файле Models.txt. Сравнительная точность прогноза, оцениваемая по квадрату коэффициента детерминации Rsquared при 10-кратной перекрестной проверке (ось Y) и на контрольной выборке из 140 наблюдений (ось X), представлена на рис. 4.18:

Models <- read.delim('Models.txt', header = TRUE)
plot(Models$Rsq,Models$Rsquared, pch = CIRCLE <- 16, 
     col = 8 - Models$col, cex = 2.5,
     xlab = "Rsquared на дополнительной выборке", 
     ylab = "Rsquared при кросс-проверке")
text(Models$Rsq, Models$Rsquared, rownames(Models), 
     pos = 4, font = 4, cex = 0.8)
legend('bottomright', c('Бэггинг/бустинг', 'Деревья',
                        'Регрессия kNN', 'PLS/PCR', 'Лассо', 'Линейные модели'),
       col = 2:7, pch = CIRCLE <- 16, cex = 1)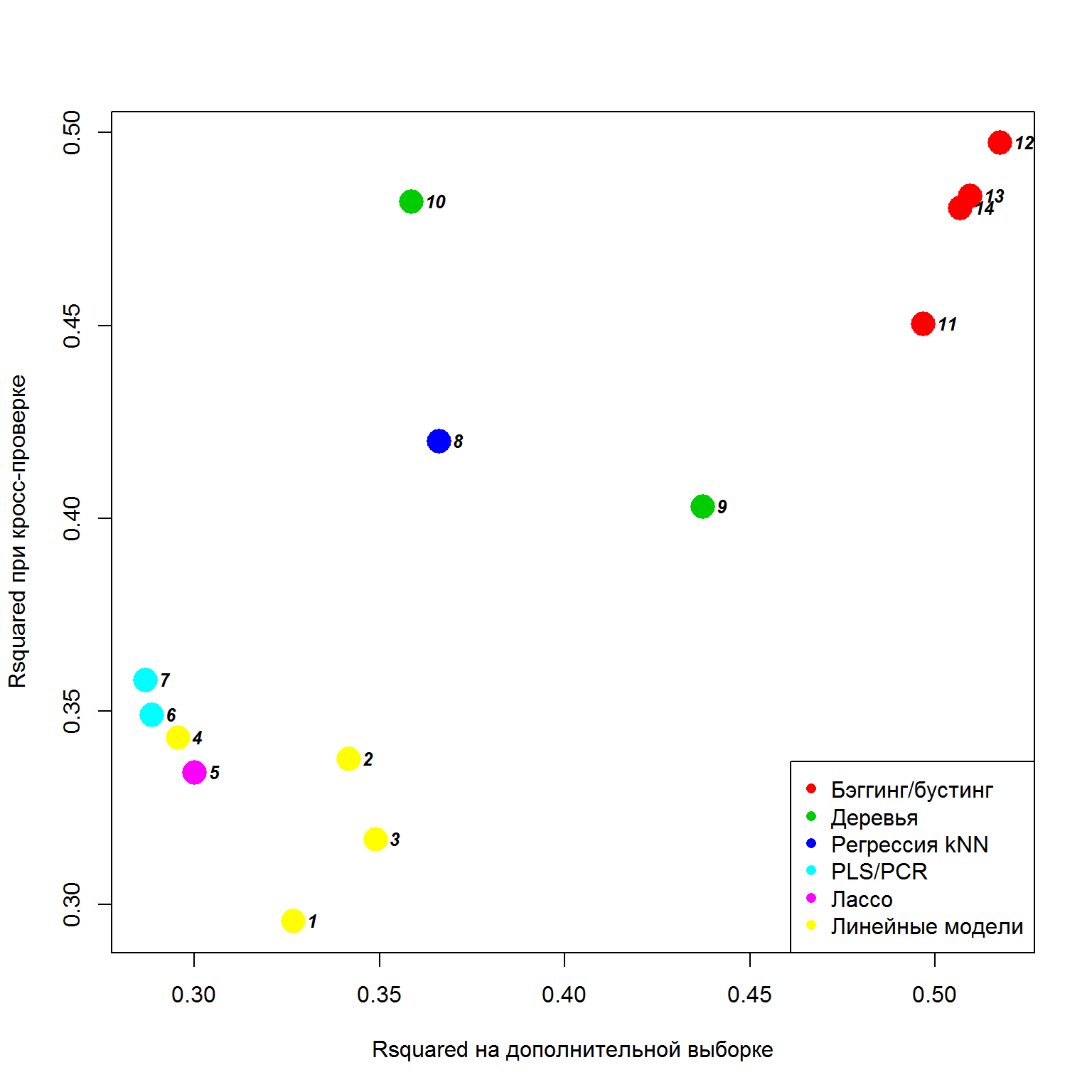
Результаты тестирования точности моделей регрессии различного класса при кросс-проверке и на внешнем дополнении

Рисунок 4.18: Результаты тестирования точности моделей регрессии различного класса при кросс-проверке и на внешнем дополнении

Хотя использованный тестовый пример представляется вполне типичным, отсутствие повторностей нашего вычислительного эксперимента не дает нам права делать далеко идущие выводы. Однако некоторые достоинства и недостатки отдельных типов прогнозирующих моделей проявились достаточно четко.

Бесспорными лидерами по точности прогноза явились модели случайного леса (12), бустинга (13-14) и бэггинга (11), основанные на ансамблях деревьев решений. Неплохо себя проявили также одиночные деревья и регрессия k ближайших соседей. Модели, основанные на обобщенных характеристиках обучающей выборки или ее преобразованиях, такие как регрессия на главные компоненты (7), PLS, лассо, дерево условного вывода (10), показали сравнительно неплохие результаты при перекрестной проверке, но оказались не столь хорошими “предсказателями” на “свежих” данных, возможно, не столь похожих на обучающие.

Метод случайного леса не только позволяет построить превосходные модели прогнозирования, но и выполнить такую работу, как селекция набора всех информативных признаков (finding all relevant variables). В общем случае эта проблема решается с использованием трех возможных подходов (https://habrahabr.ru/post/264915/):

  • методы фильтрации (filter methods), которые рассматривают каждую переменную независимо и, в некоторой степени, изолированно, оценивая ее по тому или иному показателю (информационные или статистические критерии, минимальная избыточность при максимальной релевантности mRmR и др.);
  • адаптационные методы (wrapper methods), осуществляющие направленный перебор разных подмножеств признаков и оценка их по заданному критерию (в разделе 4.1 рассматривались три таких алгоритма: пошаговый, генетический и RFE);
  • встроенные методы (embedded methods), когда отбор признаков производится неотделимо от процесса обучения модели (основным алгоритмом является регуляризация - см. метод лассо в разделе 4.2).

В адаптационных методах требуется регрессионная модель (или классификатор), которая используется как черный ящик, возвращая признаки, ранжированные по какому-нибудь удобному критерию - см. рис. 4.15. По практическим соображениям эта модель должна быть в вычислительном отношении быстрой, эффективной и простой, а также мало зависящей от параметров пользователя. Пакет Boruta (бог леса в славянской мифологии), включающий одноименную функцию, реализует адаптационный алгоритмдля модели случайного леса (Kursa, Rudnicki, 2010).

Как и функция varImp() из пакета caret, функция Boruta() оценивает меру информативности каждой переменной в виде дополнительной ошибки регрессии, вызванной исключением этой переменной из модели. Среднее \(\mu\) этой дополнительной ошибки и его стандартное отклонение \(\sigma\) рассчитываются по всем деревьям в лесу, которые используют оцениваемый признак для прогнозирования. Оценка \(Z = \mu / \sigma\) может непосредственно использоваться для ранжирования признаков, однако она не является мерой статистической значимости, поскольку не распределена нормально.

Для того, чтобы оценить, является ли ценность признака существенной, а не обусловленной случайными флуктуациями (т.е. проверить гипотезу \(H_0: Z = 0\)), алгоритм Boruta использует внешнее дополнение, полученное в ходе рандомизации. Исходная таблица переменных расширяется таким образом, что в пару каждому предиктору создается соответствующий “теневой” (shadow) признак, вектор которого получен случайным перемешиванием значений основного признака между строками. Для таких признаков корреляция с откликом отсутствует. Далее запускается алгоритм множественного построения моделей с использованием этой вдвое расширенной таблицы и вычисляется ценность всех признаков \(Z\).

Информативная ценность теневого признака может отличаться от нуля только из-за случайных флуктуаций, поэтому множество значений \(Z\) теневых признаков служит эталоном того, чтобы решить, какие признаки действительно информативны. Для этого вычисляется “теневой порог” \(MZSA\) (maximum Z score among shadow attributes) и признаки, для которых \(Z > MZSA\) объявляются значимо важными (important), в то время как остальные - незначимыми (unimportant). Поскольку Boruta - высокозатратный с вычислительной точки зрения алгоритм и не всегда удается за счет неполного числа итераций Random Forrest достичь полной ясности, некоторые признаки могут быть обозначены как неопределенные (tentative).

Используем метод Boruta для оценки важности предикторов, определяющих обилие водорослей в реках разного типа.

load(file = "algae.RData") # Загрузка таблицы algae - раздел 4.1
library(Boruta)
algae.mod <- as.data.frame(model.matrix(a1 ~ ., data = algae[, 1:12])[, -1])
algae.mod <- cbind(algae.mod, a1 = algae$a1)
set.seed(1)
algae.Boruta <- Boruta(a1 ~ ., data = algae.mod, 
                       doTrace = 2, ntree = 500)
getConfirmedFormula(algae.Boruta) 
## a1 ~ sizesmall + mxPH + Cl + NO3 + NH4 + oPO4 + PO4 + Chla
## <environment: 0x00000000072aea50>

Таким образом, в результате 99 итераций создания моделей Random Forrest по 500 деревьев в каждой статистически значимыми были признаны 7 переменных,7 которые были включены в объект formula. Статистические показатели важности признаков можно получить в виде таблицы:

attStats(algae.Boruta)
##                 meanImp  medianImp     minImp    maxImp   normHits
## seasonspring  0.5693189  0.4069052 -0.8649699  2.075703 0.01010101
## seasonsummer -0.1596926 -0.3499825 -1.5728241  1.725287 0.00000000
## seasonwinter -0.1775464 -0.4018779 -1.1984788  1.972420 0.00000000
## sizemedium    0.9838655  0.8715906 -0.2870415  2.419892 0.01010101
## sizesmall     3.5793482  3.5483906  1.5546458  5.816447 0.71717172
## speedlow      1.6607858  1.6797431 -0.5456829  3.255695 0.05050505
## speedmedium   2.1834842  2.2534784 -0.7136495  4.253952 0.43434343
## mxPH          4.6814562  4.7170495  1.9551148  6.671736 0.89898990
## mnO2          2.1644531  2.1459241 -1.8856452  4.411559 0.38383838
## Cl           12.2427594 12.2077849 10.0451025 14.133899 1.00000000
## NO3           4.6025536  4.6809829  2.1551312  6.578464 0.88888889
## NH4          11.5330358 11.5867263  9.6825814 13.451071 1.00000000
## oPO4         14.1610413 14.1254230 12.6569532 16.251786 1.00000000
## PO4          16.3344698 16.4004710 14.2130314 18.726623 1.00000000
## Chla          7.5156732  7.6125418  4.8295387  9.419857 1.00000000
##               decision
## seasonspring  Rejected
## seasonsummer  Rejected
## seasonwinter  Rejected
## sizemedium    Rejected
## sizesmall    Confirmed
## speedlow      Rejected
## speedmedium  Tentative
## mxPH         Confirmed
## mnO2         Tentative
## Cl           Confirmed
## NO3          Confirmed
## NH4          Confirmed
## oPO4         Confirmed
## PO4          Confirmed
## Chla         Confirmed

Разумеется, более наглядно результаты выглядят на диаграмме (рис. 4.19). К сожалению, разработчики пакета сделали трудночитаемым перечень предикторов по оси Х, и нам пришлось немного повозиться, чтобы исправить этот недостаток:

plot(algae.Boruta, xlab = "", xaxt = "n")
lz <- lapply(1:ncol(algae.Boruta$ImpHistory), function(i)
    algae.Boruta$ImpHistory[is.finite(algae.Boruta$ImpHistory[, i]) , i])
names(lz) <- colnames(algae.Boruta$ImpHistory)
Labels <- sort(sapply(lz,median))
axis(side = 1, las = 2, labels = names(Labels),
     at = 1:ncol(algae.Boruta$ImpHistory), cex.axis = 0.7)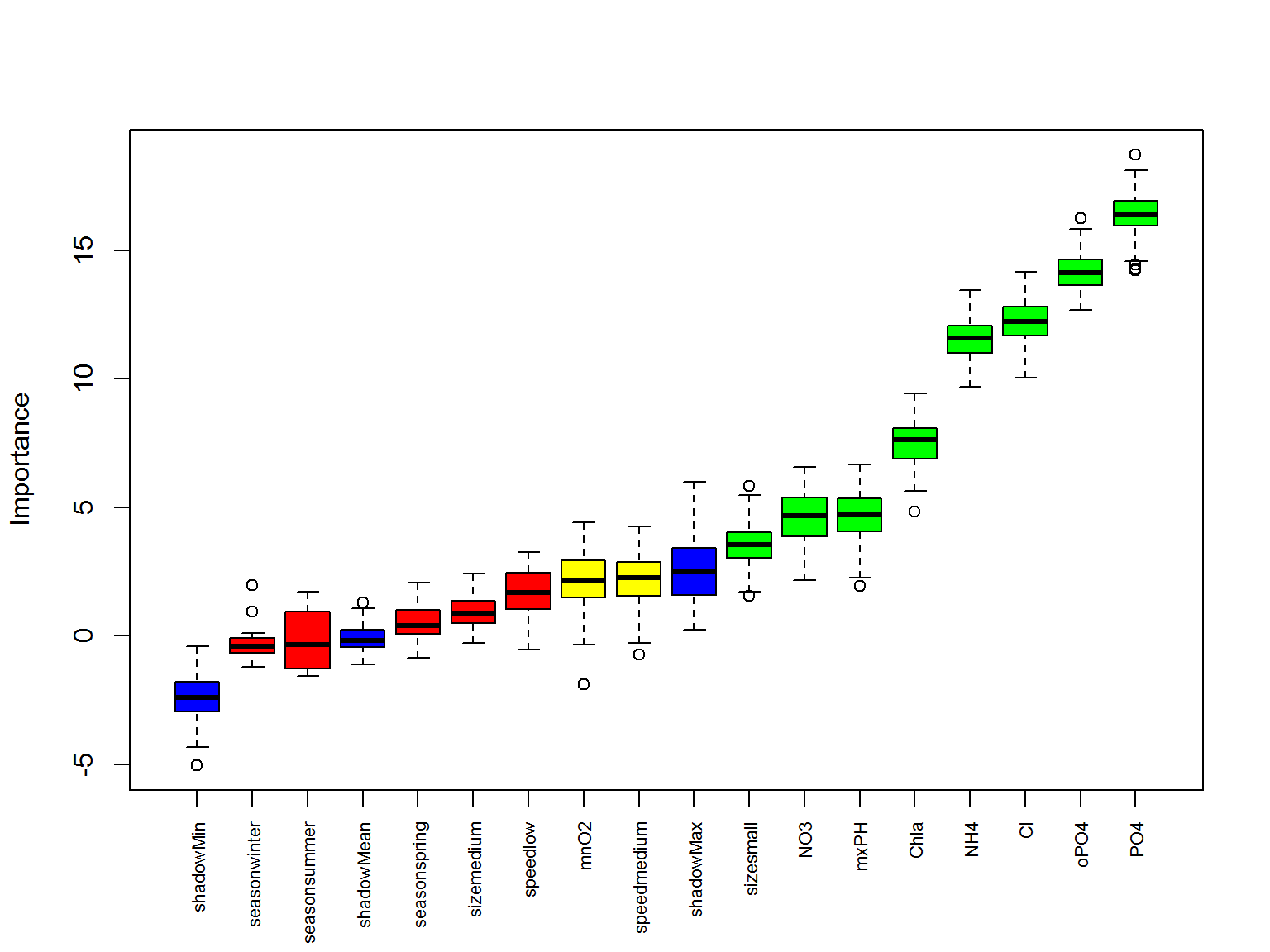
Ранжирование предикторов с использованием алгоритма Boruta; синим цветом показана важность для значений теневых признаков

Рисунок 4.19: Ранжирование предикторов с использованием алгоритма Boruta; синим цветом показана важность для значений теневых признаков

Представленный ранжированный перечень предикторов достаточно близок (хотя и в разной степени) наборам информативных переменных, сформированным другими методами селекции в разделах выше. Однако оценки значимости придают алгоритму Boruta несомненное преимущество.

  1. Полученный вами результата может отличаться от приведенного в силу случайного характера подвыборок, формируемых в ходе выполнения алгоритма↩