Классификация, регрессия и другие алгоритмы Data Mining с использованием R

9.5 Неметрическое многомерное шкалирование и построение распределения чувствительности видов

Перспективным методом ординации, находящим все большее применение в различных предметных областях, является алгоритм неметрического многомерного шкалирования (NMDS, nonmetric multidimensional scaling – Краскел, 1986; McCune, Grace, 2002). Его главным преимуществом является то, что он не требует от исходных данных никаких априорных предположений о характере статистического распределения. Считается, что этот метод дает наиболее адекватные результаты, особенно для больших матриц с сильными “шумами”.

Неметрическое шкалирование, как и метод главных координат, использует произвольную матрицу дистанций \(\mathbf{D}\) и ставит задачу создать такую двумерную проекцию изучаемых объектов, на которой взаимные расстояния между этими объектами оказались бы наименее искажены по сравнению с исходным состоянием \(\mathbf{D}\). Главные оси геометрической метафоры данных в пространстве меньшей размерности обычно находят путем выполнения последовательности итераций для минимизации критерия \(\Delta\), оценивающего меру расхождений между исходной и моделируемой матрицами расстояний. Для этого обычно используют величину “стресса”:

\[\Delta = \sum_{i,j=1}^n d_{ij}^{\alpha} |\hat{d}_{ij} - d_{ij}|^{\beta},\]

где \(d_{ij}\) и \(\hat{d}_{ij}\) - расстояния между объектами \(i\) и \(j\) в исходном и редуцированном пространствах, \(\alpha\) и \(\beta\) - задаваемые коэффициенты.

Пакет vegan содержит ряд функций для проведения расчетов методом NMDS и построения объясняющих ординаций. Рассмотрим пример, включающий наборы данных varespec и varechem, которые использовались нами в предыдущем разделе для ординации каноническим методом CCA, основанным на линейных преобразованиях. На первом этапе определим наилучшую метрику расстояния, рассчитав для каждого из ее вариантов коэффициент корреляции Спирмена между двумя матрицами дистанций (в пространствах видов растительности и химического состава почвы). Эту операцию выполняет функция rankindex():

library(vegan)
data(varechem)
data(varespec)
varespec.chi <- decostand(varespec, method = "chi.square")
# Коэффициенты корреляции Спирмена для различных метрик 
rankindex(varechem, varespec.chi, c("euc", "man", "bray", "jac", "kul"))

##       euc       man      bray       jac       kul 
## 0.2228233 0.1894385 0.3022988 0.3022988 0.3071600

Используем для расчета матрицы дистанций формулу Кульчицкого. Далее функция metaMDS() осуществляет неметрическое шкалирование и минимизацию стресса \(\Delta\), а функция envfit() - расчет коэффициентов корреляции каждого из показателей химического состава почвы с осями ординации NMDS1-NMDS2 и оценку статистической значимости \(p\) этих коэффициентов на основе перестановочного теста. Функция MDSrotate() вращает систему координат таким образом, чтобы совместить ось NMDS1, например, с осью концентрации алюминия:

vare.mds <- metaMDS(varespec,distance = "kul", trace = FALSE) 
ord.mds <- MDSrotate(vare.mds, varechem$Al)
set.seed(2)
ef <- envfit(vare.mds, varechem, permu = 999)

Построим ординационные диаграммы с использованием стандартных графических средств R (как это можно сделать на основе ggplot2 см. <github.com/gavinsimpson/ggvegan>, chrischizinski.github.io или stackoverflow.com). Первая диаграмма (рис. 9.13) включает ординацию площадок и оси девяти внешних факторов, для которых \(p < 0.1\).

plot(vare.mds, type = "t", disp = "sites", font = 2)  
points(vare.mds, disp = "sites", cex = 3, col = "red")
abline(h = 0, lty = 3)
abline(v = 0, lty = 3)
plot(ef, p.max = 0.1, col = "blue", font = 2, lwd = 2, cex = 1)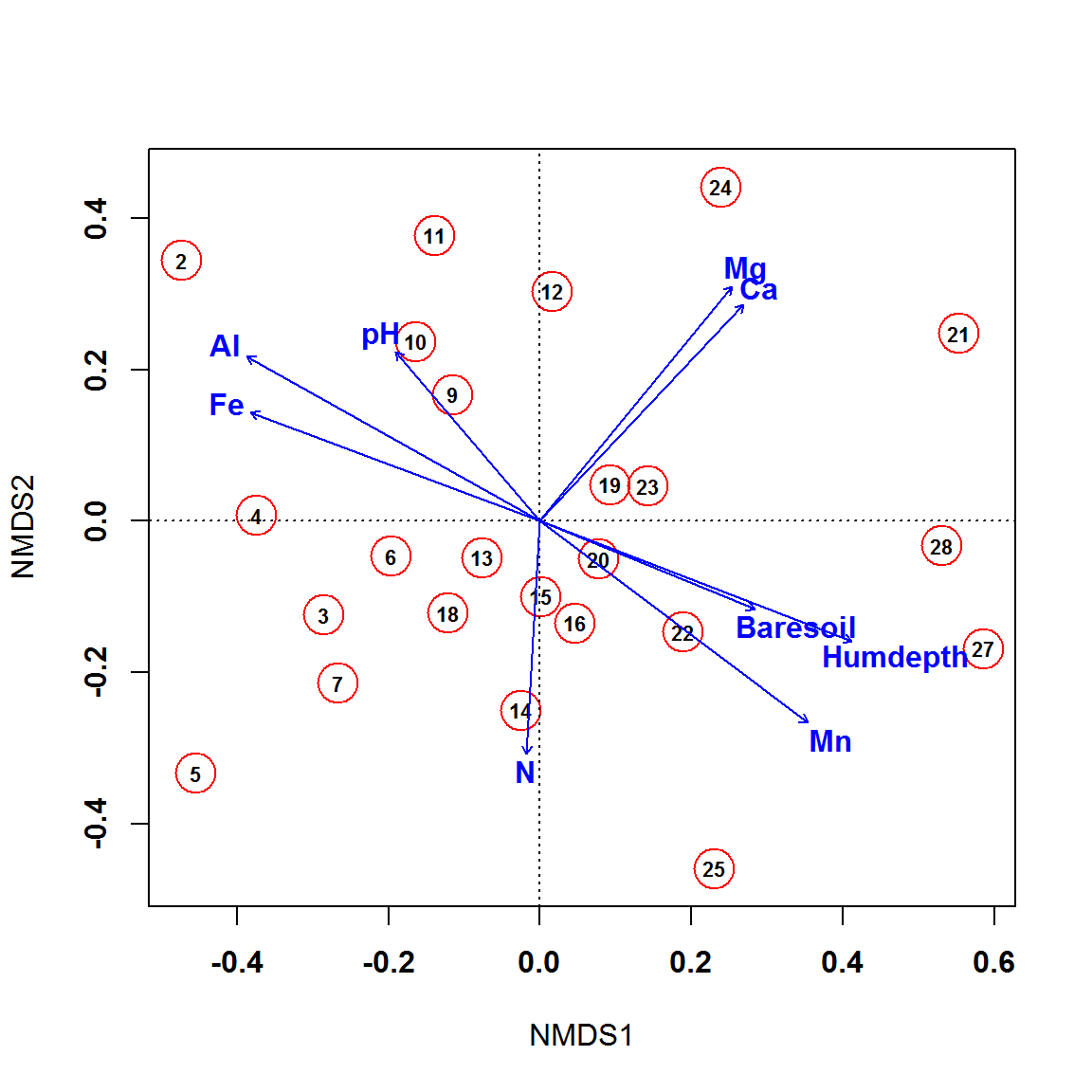

Рисунок 9.13: Ординация площадок, полученная методом NMDS

Прежде чем построить вторую диаграмму, для концентрации \(y_{хэ}\) в почве того или иного химического компонента по его эмпирическим значениям для каждой площадки подгонялись обобщенные аддитивные модели (Wood, 2006):

\[y_{хэ} = s(\nu_1, \nu_2) + \epsilon, \quad (9.4)\]

где \(s\) - функция двумерного сплайна с \(k\) степенями свободы от NMDS-координат \(\nu_1\) и \(\nu_2\). Построение этой модели осуществляется функцией ordisurf(), которая параллельно отрисовывает изолинии трехмерной сглаживающей поверхности на ординационной диаграмме.

Обратим особое внимание на отличие описываемого метода от обычных пространственных моделей кригинга в естественных географических координатах, которые сильно подвержены случайным флуктуациям свойств рельефа. Построение моделей сглаживания по проекциям матрицы отклика на плоскость с абстрактными осями, непосредственно связанными с изучаемой экологической структурой, обеспечивает получение более гладких и устойчивых поверхностей.

На рис. 9.14 показано, как на ординацию видов растительности могут быть наложены изолинии по моделям сглаживания содержания Al и Ca.

plot(vare.mds,  type = "n") 
ordipointlabel(vare.mds, display = "sp", font = 4, col = "darkgreen", add = TRUE)
abline(h = 0, lty = 3)
abline(v = 0, lty = 3)
with(varechem, ordisurf(vare.mds, Al, add = TRUE, col = 2))

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## y ~ s(x1, x2, k = 10, bs = "tp", fx = FALSE)
## 
## Estimated degrees of freedom:
## 4.77  total = 5.77 
## 
## REML score: 139.4294

with(varechem, ordisurf(vare.mds, Ca, add = TRUE, col = 4))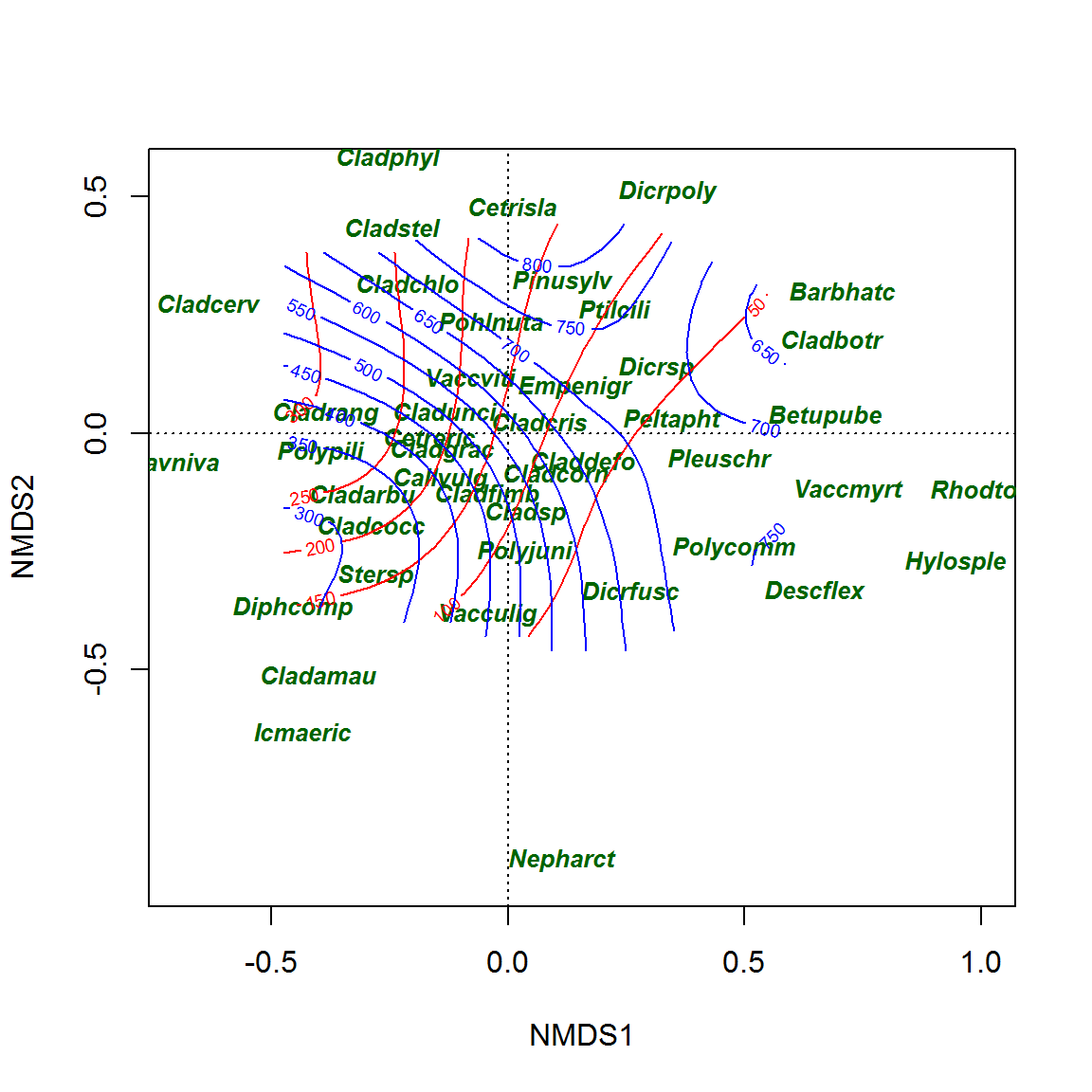

Рисунок 9.14: Ординация видов методом NMDS и изолинии сглаживающих поверхностей для Al и Ca

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## y ~ s(x1, x2, k = 10, bs = "tp", fx = FALSE)
## 
## Estimated degrees of freedom:
## 4.72  total = 5.72 
## 
## REML score: 156.6547

Вероятно, можно предположить (по крайней мере, в рамках имеющейся выборки), что каждая точка ординации, соответствующая тому или иному виду, определяет координаты наилучших природных условий существования этого вида, а прогнозное значение модели (9.4) оценивает его экологический оптимум по сглаживаемому фактору. Функция calibrate(mod, newdata), аналогичная функции predict(), осуществляет с использованием модели mod вычисление для произвольной таблицы newdata прогнозных значений и их стандартных ошибок se.fit.

Оценим экологические оптимумы val содержания алюминия Al в почве для каждого обнаруженного вида растительности. Вычислим также верхние 95%-ные доверительные границы предсказания valC по формуле valC = val + tc*se.fit, где tc - квантиль распределения Стьюдента при \(\alpha = 95\%\). Чтобы блокировать появление отрицательных значений, значение внешнего фактора предварительно прологарифмируем.

Al.log <- log(varechem$Al)
fit.Al <- ordisurf(vare.mds, Al.log, plot = FALSE)
a <- as.data.frame(vare.mds$species)
Sp.Al <- cbind(a, calibrate(fit.Al, newdata = a, se.fit = TRUE))
Sp.Al$val <- exp(Sp.Al$fit)
tc <- qt(0.975, nrow(Sp.Al) - 1)
Sp.Al$valC <- exp(Sp.Al$fit) + exp(Sp.Al$se.fit)*tc
head(Sp.Al)

##                 MDS1        MDS2      fit    se.fit        val      valC
## Callvulg -0.14394845 -0.05558775 4.994819 0.1895819 147.646179 150.08384
## Empenigr  0.01355070  0.06669567 4.667149 0.1949377 106.394015 108.84477
## Rhodtome  0.88525555 -0.08405623 2.137824 0.5238554   8.480966  11.88620
## Vaccmyrt  0.71804957 -0.08029688 2.509319 0.4298838  12.296553  15.39637
## Vaccviti  0.02603872  0.08769089 4.656761 0.2004028 105.294429 107.75861
## Pinusylv -0.01228925  0.31966150 5.090535 0.2580998 162.476707 165.08725

Одним из методов нормирования техногенных загрязнений на исследуемой территории является построение статистических моделей распределения чувствительности видов SSD (Species Sensitivity Distribution; Posthuma et al., 2001). Кривая SSD рассчитывается как интегральная функция некоторого теоретического распределения плотности вероятности встречаемости видов, параметры которого оцениваются по выборке того или иного показателя жизнедеятельности таксономических групп (чаще всего для этого используются показатели токсикометрии \(NOEC\), \(DС_{50}\), \(LС_{50}\) и т.д.).

Поскольку для травянистых растений параметры токсичности отсутствуют, то в качестве предположительно опасных значений содержания алюминия в почве для \(j\)-го вида примем настолько большие его величины, которые маловероятны в рамках сглаживающей модели GAM, т.е. столбец valC сформированной таблицы Sp.Al. Если отсортировать этот показатель по его величине, то функция ppoints() сгенерирует последовательность эмпирических вероятностей frac, т.е. долю значений valC, которые не превышают величину valC для каждого \(j\)-го вида.

# Сортировка по возрастанию val 
df <- Sp.Al[, 5:6]
df <- df[order(df$val), ]
df$frac <- ppoints(df$val, 0.5)
head(df)

##                val      valC       frac
## Hylosple  5.384064  8.998957 0.01136364
## Nepharct  6.286644 10.508728 0.03409091
## Descflex  6.968646 10.326709 0.05681818
## Rhodtome  8.480966 11.886201 0.07954545
## Polycomm 10.540915 13.629360 0.10227273
## Vaccmyrt 12.296553 15.396368 0.12500000

Для аппроксимации данных теоретическим распределением воспользуемся функцией fitdist() из пакета fitdistplus. Наилучшая аппроксимация, процедуру подбора которой мы опускаем, соответствует логнормальному распределению. Найдем параметры этого распределения, т.е. оценки среднего meanlog и дисперсии sdlog, а также некоторые квантильные значения Al.

library(fitdistrplus)
(fit <- fitdistr(df$valC, "lognormal"))

##     meanlog      sdlog  
##   4.2881216   1.0052990 
##  (0.1515545) (0.1071652)

ep1s <- fit$estimate[1]
ep2s <- fit$estimate[2]
(hcs <- qlnorm(c(0.05, 0.1, 0.2), meanlog = ep1s, sdlog = ep2s))

## [1] 13.93707 20.08110 31.25066

Для построения кривой распределения чувствительности видов (SSD) будем использовать скрипт, представленный в блоге “Data in Environmental Science and Ecotoxicology” (http://edild.github.io/ssd/, автор E. Szöcs). Оценка доверительных интервалов теоретической кривой может быть осуществлена с использованием параметрического бутстрепа, который использует предположение о том, что исходные выборочные данные представляют собой случайные реализации вероятностного процесса, определяемого параметрами заданного распределения (Davison, Hinkley, 2006). Подробные комментарии к тексту скрипта см. в нашей книге (Шитиков, 2016).

Определим предварительно две функции, необходимые нам в основных расчетах и выполняющие генерацию псевдо-выборок:

# 1. Функция для нахождения p-квантили случайной выборки из 
#  логнормального распределения с параметрами  fit
myboot <- function(fit, p){
    xr <- rlnorm(fit$n, meanlog = fit$estimate[1], sdlog = fit$estimate[2])
    fitr <- fitdist(xr, 'lnorm')
    hc5r <- qlnorm(p, meanlog = fitr$estimate[1], sdlog = fitr$estimate[2])
    return(hc5r)
}

# 2. Функция, возвращающая значения вероятностей для случайной
#  выборки из логнормального распределения с параметрами  fit
myboot2 <- function(fit, newxs){
    xr <- rlnorm(fit$n, meanlog = fit$estimate[1], sdlog = fit$estimate[2])
    fitr <- fitdist(xr, 'lnorm')
    pyr <- plnorm(newxs, meanlog = fitr$estimate[1], sdlog = fitr$estimate[2])
    return(pyr)
}

Выполним построение 1000 бутстреп-кривых из заданного распределения и определим координаты графиков основной функции распределения и ее 95%-ных доверительных огибающих:

require(reshape2)
set.seed(1234) # Установка генератора случайных чисел

# новые данные для построения плавной кривой
newxs <- 10^(seq(log10(0.01), log10(max(df$valC)), length.out = 100))

# получение матрицы для построения 1000 кривых
boots <- replicate(1000, myboot2(fit, newxs))
bootdat <- data.frame(boots)
bootdat$newxs <- newxs
bootdat <- melt(bootdat, id = 'newxs')

# извлечение доверительных интервалов
cis <- apply(boots, 1, quantile, c(0.025, 0.975))
rownames(cis) <- c('lwr', 'upr')

# Формирование итоговой таблицы подогнанных значений и  cis
pdat <- data.frame(newxs, 
                   py = plnorm(newxs, meanlog = fit$estimate[1],
                               sdlog = fit$estimate[2]))
pdat <- cbind(pdat, t(cis))

# координаты x для названия видов
df$fit <- 10^(log10(qlnorm(df$frac, 
                           meanlog = fit$estimate[1], 
                           sdlog = fit$estimate[2])) - 0.4)

Осуществим вывод полноценного графика SSD с использованием пакета ggplot2 (рис. 9.15):

library(ggplot2)
ggplot() +
    geom_line(data = bootdat, aes(x = newxs, y = value, group = variable), 
              col = 'steelblue', alpha = 0.05) +
    geom_point(data = df, aes(x = valC, y = frac)) +
    geom_line(data = pdat, aes(x = newxs, y = py), col = 'red') +
    geom_line(data = pdat, aes(x = newxs, y = lwr), linetype = 'dashed') +
    geom_line(data = pdat, aes(x = newxs, y = upr), linetype = 'dashed') +
    geom_text(data = df, aes(x = fit, y = frac, label = rownames(df)), 
              hjust = 1, size = 4) +
    scale_x_log10(breaks = c(5,  10, 50, 100, 300), limits = c(1, max(df$valC))) +
    labs(x = 'Содержание алюминия в почве',
         y = 'Доля видов с неблагоприятными условиями') + theme_bw()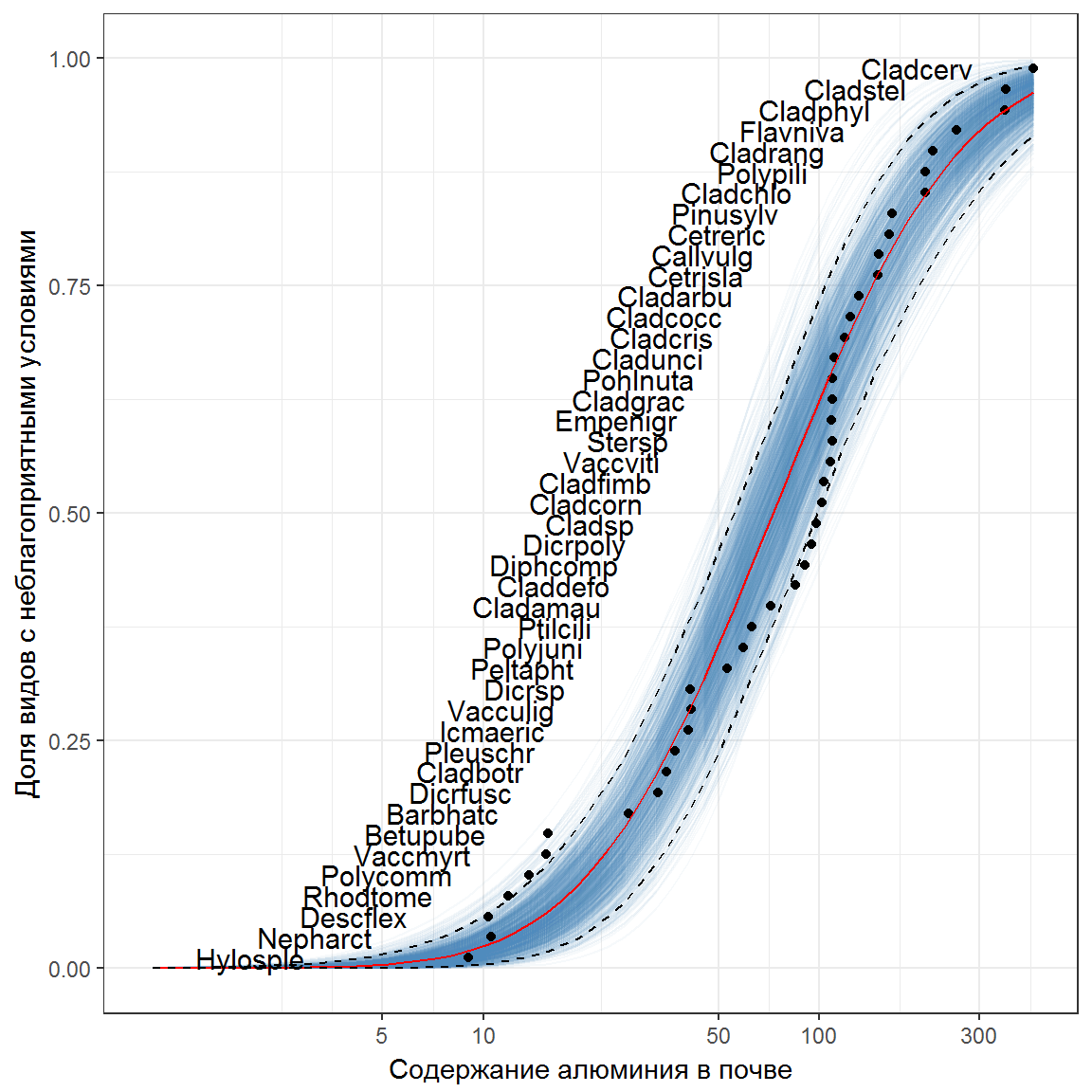

Рисунок 9.15: Распределение чувствительности видов в зависимости от содержания алюминия в почве

Если задаться произвольной критической вероятностью на оси ординат SSD (см. рис. 9.15), то с использованием кумулятивной кривой распределения можно оценить величину потенциально опасного уровня воздействия внешнего фактора (Шитиков, 2016). Из представленных результатов следует, что уже при содержании алюминия в почве Al = {13.9, 20.1 и 31.3} из травянистого сообщества могут исчезнуть соответственно доли р = {5, 10, и 20%} видов от их общего числа.

Конечно, мы здесь не собирались делать каких-либо конкретных выводов в отношении вредности для растений тех или иных ингредиентов в почве, и даже не исключаем, что алюминий полезен для травостоя. Мы только использовали этот пример, чтобы описать реализацию в R алгоритмов ординации многомерных данных, подбора параметров статистических распределений и оценки степени критичности воздействия внешнего фактора.

Поскольку современные тенденции исследований связаны с интенсивным заимствованием методов и приемов из разнородных отраслей, описанные алгоритмы ординации, вероятно, пригодны для использования не только в экологических приложениях. Например, в социологических исследованиях виды растений можно вполне заменить наблюдаемыми предпочтениями избирателей в отношении потенциальных кандидатур на ту или иную должность. А интенсивность ремонта дорог может служить важным внешним фактором, обусловливающим вероятность победы на выборах желаемого кандидата.