10.2 Иерархическая кластеризация

Методы иерархической кластеризации основываются на двух идеях: агломерации (AGNES, Agglomerative Nesting), т.е. последовательного объединения индивидуальных объектов или их групп во все более крупные подмножества, или обратном по смыслу процессе разбиения (DIANA, Divise Analysis), который начинается с корня и на каждом шаге делит образующие группы по степени их гетерогенности (Ким и др., 1989; Kassambara, 2017). В обоих случаях результат работы алгоритма представляет собой древовидную структуру, или дендрограмму.

Отдельные версии агломеративной иерархической процедуры отличаются правилами вычисления расстояния между кластерами. Например, алгоритм средней связи (average linkage clustering) на каждом следующем шаге объединяет два ближайших кластера, рассчитывая среднюю арифметическую дистанцию между всеми парами объектов. К алгоритму средней связи естественно сразу добавить еще два со взаимно противоположными тенденциями:

• алгоритм одиночной связи, или “ближайшего соседа” (single linkage clustering), когда расстояние между кластерами оценивается как минимальное из дистанций между парами объектов, один из которых входит в первый кластер, а другой - во второй;
• и алгоритм полной связи или “дальнего соседа” (complete linkage clustering), когда вычисляется расстояние между наиболее удаленными объектами.

Более глубокий статистический смысл в понятие расстояния между кластерами вкладывается при использовании центроидного метода (centroid linkage clustering) и метода минимума дисперсии Уорда (Ward).

Утверждать, какой из методов предпочтительней, довольно просто - это тот, который чаще всего приводит к естественной кластеризации. Однако имеющиеся огромные расхождения в понимании столь тонкого предмета, как “естественность”, вынуждают признать этот термин нечетким. Поэтому мы ограничимся в этом разделе лишь анализом сходства результатов кластеризации, полученных различными алгоритмами.

Предварительно рассмотрим функции, которые используют в R для проведения иерархической кластеризации:

hclust(d, method = "complete")
agnes(x, metric = "euclidean", stand = FALSE, method = "average")
diana(x, metric = "euclidean", stand = FALSE)

где

• d: матрица дистанций, полученная функцией dist() или как-то иначе;
• method: метод агломерации, определяемый одним из значений "ward.D", "ward.D2", "single", "complete", "average", "mcquitty", "median" или "centroid";
• x: таблица данных для вычисления расстояний (наблюдения - по строкам, признаки - по столбцам);
• metric: метрика расстояний между наблюдениями, т.е. "euclidean" или "manhattan";
• stand = TRUE: осуществляется стандартизация каждой переменной таблицы (по столбцам).

Очевидно, что агломерационные процедуры hclust() и agnes() приведут к одному и тому же результату, а diana() выполнит алгоритм последовательного разбиения.

Приведем различные варианты формирования дендрограмм и способы их визуализации на примере кластеризации штатов США по криминогенной обстановке. Первые три диаграммы на рис. 10.7 построены с использованием базовой функции plot.hclust(), имеющей ограниченный набор настраиваемых параметров. Для варианта "complete" показан пример разрезания дерева на 4 группы, которые на дендрограмме можно показать в виде прямоугольников.

Четвертый рисунок получен с помощью функции plot.dendrogram(), которая имеет такие дополнительные параметры как nodePar - спецификацию графического изображения узлов дерева, и edgePar - список графических параметров для представления ветвей разными цветами.

library(cluster)
data("USArrests")
d <- dist(scale(USArrests), method = "euclidean")

par(mfrow = c(4, 1))
# Параметр hang=-1  выравнивает метки
plot(hclust(d, method = "average" ), cex = 0.7, hang = -1)
plot(hclust(d, method = "single" ), cex = 0.7)

res.hc <- hclust(d, method = "complete" )
grp <- cutree(res.hc, k = 4)  # Разрезание дерева на 4 группы
plot(res.hc, cex = 0.7)
rect.hclust(res.hc, k = 4, border = 2:5)

hcd <- as.dendrogram(hclust(d, method = "ward.D2" ))
nodePar <- list(lab.cex = 0.7, pch = c(NA, 19), cex = 0.7, col = "blue")
plot(hcd,  xlab = "Height", nodePar = nodePar, horiz = TRUE,
     edgePar = list(col = 2:3, lwd = 2:1))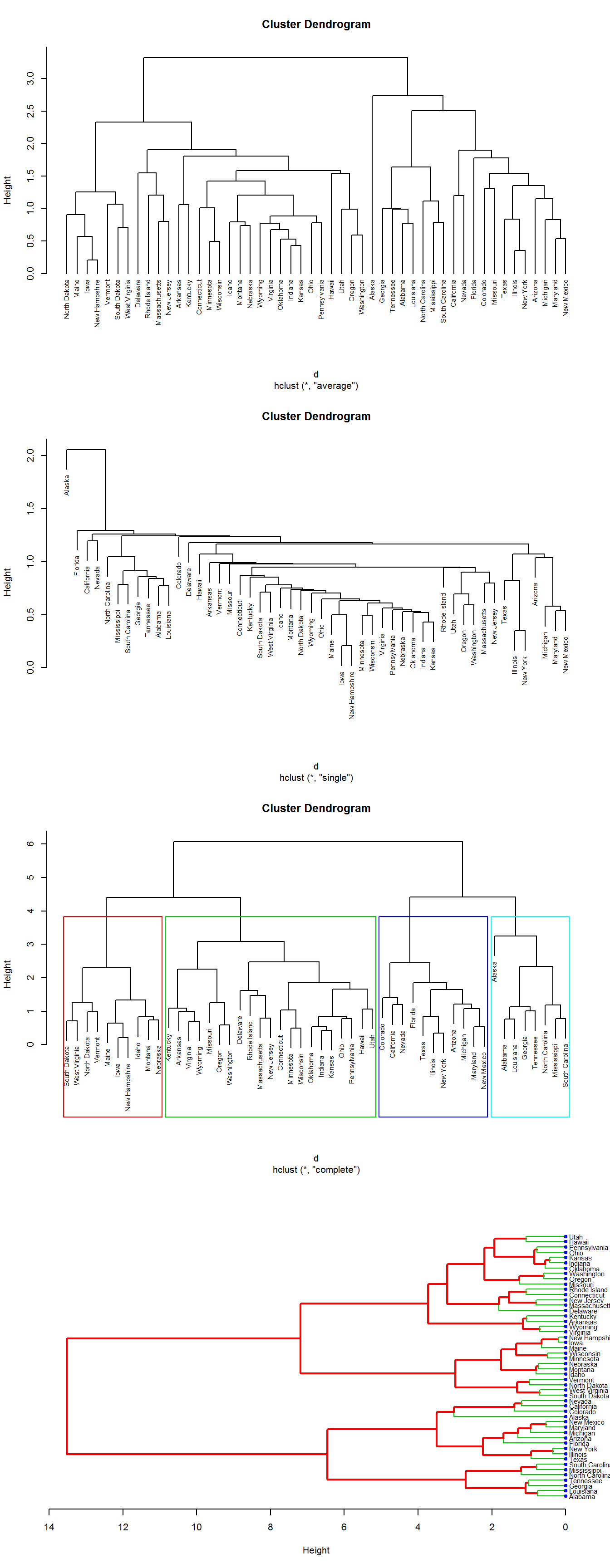

Рисунок 10.7: Дендрограмма распределения штатов США по кластерам. По порядку сверху вниз: "average" - метод средней связи, "single" - метод одиночной связи, "complete" - метод полной связи, "ward.D2" - метод Уорда

Дополнительные возможности для графического представления дендрограмм можно найти в функциях пакетов ape (анализ филогенетики и эволюции) и ggdendro, использующего графическую систему ggplot2.

Визуальные впечатления от сравнения различных дендрограмм на рис. 10.7 и опыт специалистов свидетельствует о том, что метод Уорда и полной связи дают весьма сходные результаты (к ним приближается также метод средней связи). Метод одиночной связи и центроидный метод могут дать иногда весьма специфические дендрограммы. Однако для анализа сходства дендрограмм предпочтительнее использовать пакет dendextend, который содержит несколько функций для сравнения результатов кластеризации, включая: dend_diff(), tanglegram(), entanglement(), all.equal.dendrogram(), cor.dendlist(). Выполним построение диаграммы типа “клубок”, показывающей различия двух дендрограмм:

library(dendextend)
# Вычисляем 2 иерархические кластеризации
hc1 <- hclust(d, method = "average")
hc2 <- hclust(d, method = "ward.D2")
# Создаем две дендрограммы
dend1 <- as.dendrogram(hc1)
dend2 <- as.dendrogram(hc2)
# На диаграмме типа "клубок" показываем цветом общие ветви
tanglegram(dend1, dend2, common_subtrees_color_branches = TRUE)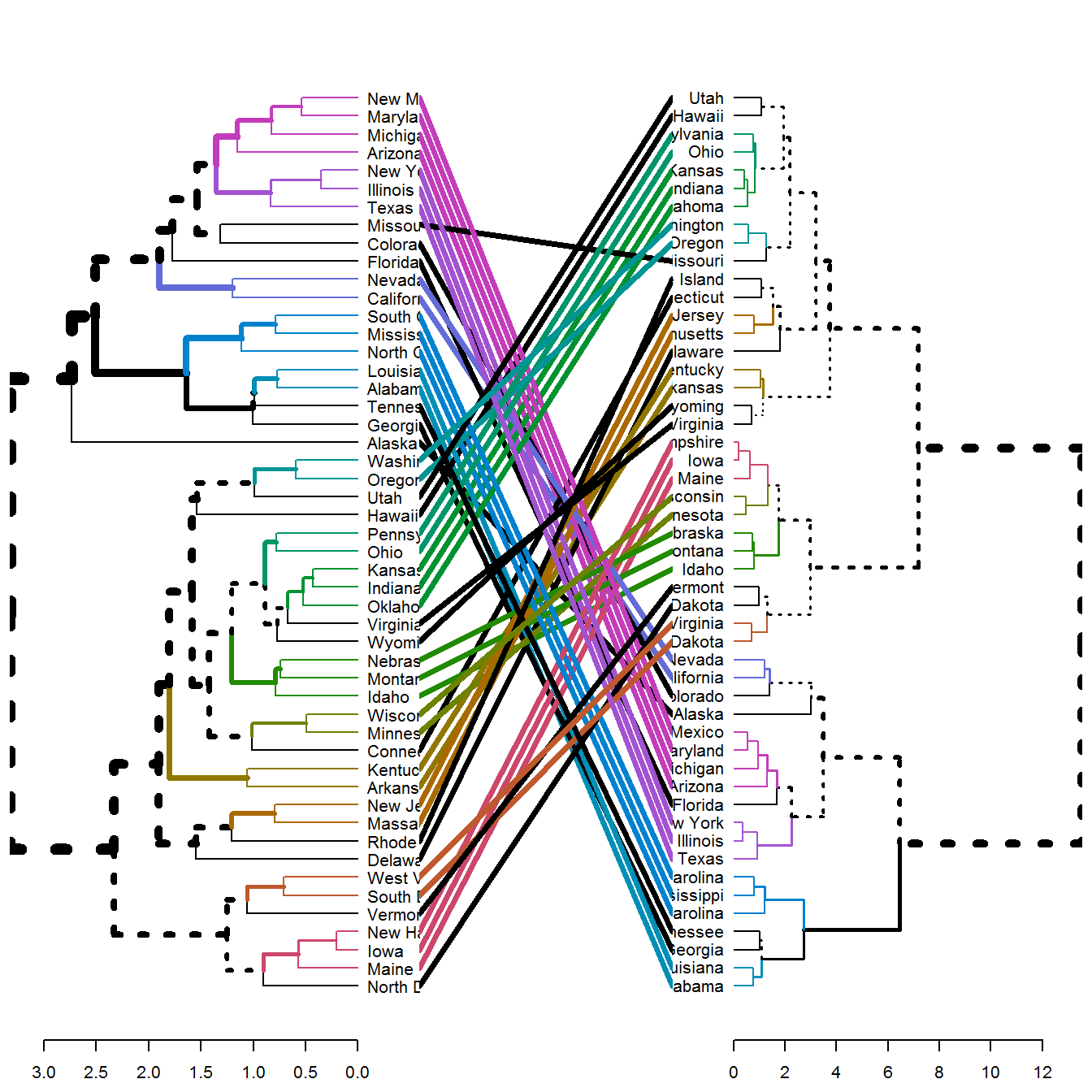

Рисунок 10.8: Диаграмма сравнения деревьев кластеризации "average"-"ward"

Для количественной оценки различий между вариантами кластеризации могут быть использованы кофенетическая корреляция (cophenetic correlation) или различные ранговые индексы. Кофенетическая дистанция определяет расстояние между двумя объектами на дендрограмме и отражает уровень внутригрупповых различий, при котором эти объекты были впервые объединены в один кластер (Ким и др., 1989). Все возможные пары таких дистанций образуют апостериорную матрицу расстояний между объектами по результатам кластеризации. Кофенетическая корреляция вычисляется как линейный коэффициент корреляции Пирсона (или ранговый коэффициент Спирмена) между всеми элементами двух таких матриц:

c(cor_cophenetic(dend1, dend2), # кофенетическая корреляция
cor_bakers_gamma(dend1, dend2))  # корреляция Бейкера

## [1] 0.8431430 0.8400675

Аналогично можно получить матрицу коэффициентов кофенетической корреляции для всех обсуждаемых методов иерархической кластеризации (рис. 10.9):

# Создаем множество дендрограмм для сравнения
dend1 <- d %>% hclust("com") %>% as.dendrogram
dend2 <- d %>% hclust("single") %>% as.dendrogram
dend3 <- d %>% hclust("ave") %>% as.dendrogram
dend4 <- d %>% hclust("centroid") %>% as.dendrogram
dend5 <- d %>% hclust("ward.D2") %>% as.dendrogram

# Создаем список дендрограмм и корреляционную матрицу
dend_list <- dendlist("Complete" = dend1, "Single" = dend2,
     "Average" = dend3, "Centroid" = dend4, "Ward.D2" = dend5)
cors <- cor.dendlist(dend_list)
round(cors, 2)

##          Complete Single Average Centroid Ward.D2
## Complete     1.00   0.50    0.86     0.49    0.94
## Single       0.50   1.00    0.58     0.71    0.49
## Average      0.86   0.58    1.00     0.61    0.84
## Centroid     0.49   0.71    0.61     1.00    0.49
## Ward.D2      0.94   0.49    0.84     0.49    1.00

library(corrplot) # изображение корреляционной матрицы
corrplot(cors, "pie", "lower")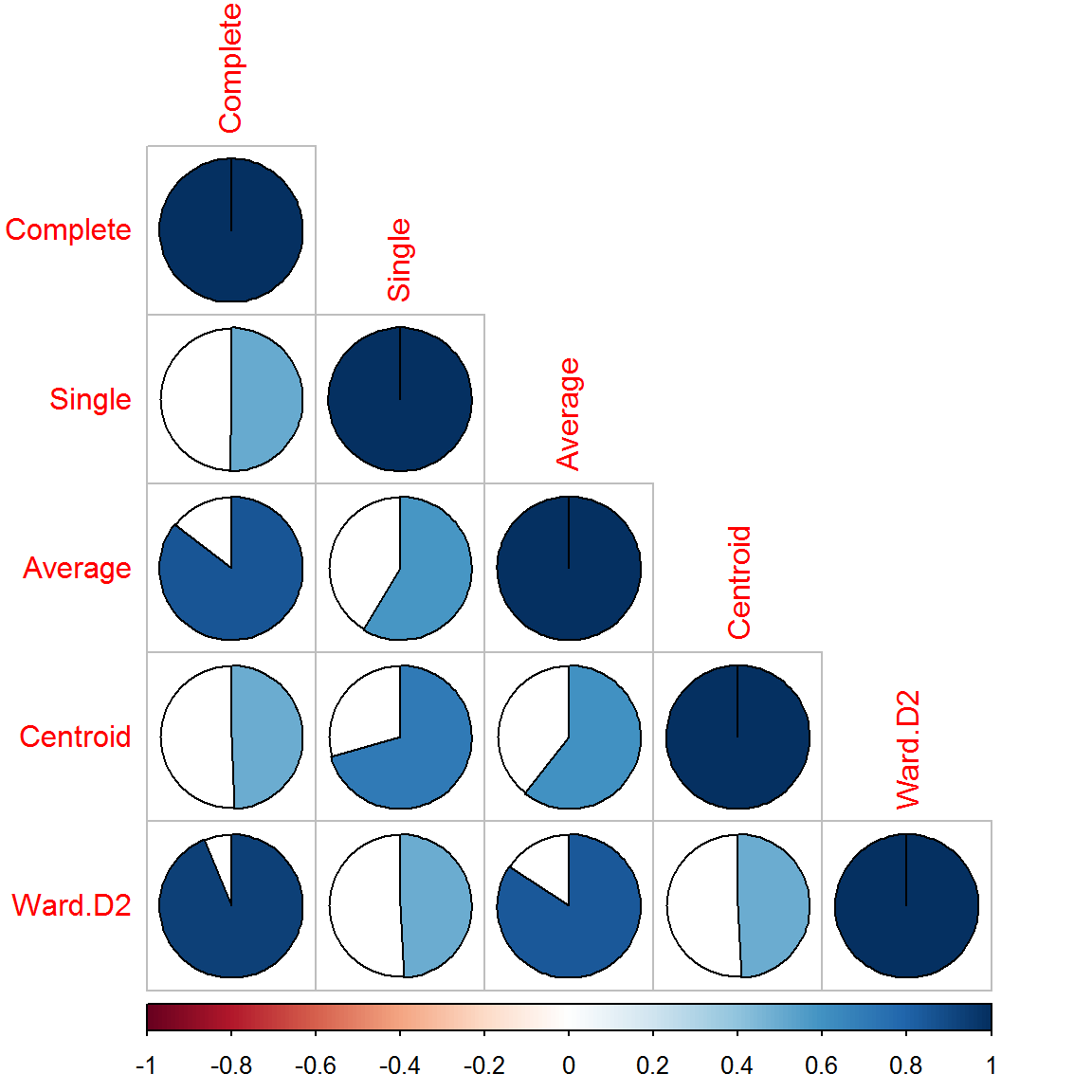

Рисунок 10.9: Корреляция между кластеризациями на основе разных методов