Классификация, регрессия и другие алгоритмы Data Mining с использованием R

8.4 Обобщенные линейные модели для счетных данных

В предыдущих главах нами рассматривались примеры использования методов построения моделей для различных типов распределения отклика. При этом значительная часть реальных наблюдений сводится к подсчету числа экземпляров: это могут быть обследуемые респонденты, проданные гаджеты, тыс. клеток водорослей, нажатия кнопок мыши или птицы, пролетающие мимо наблюдателя. Эти данные по своей природе дискретны и может возникнуть вопрос, а какое распределение выбрать для их описания?

Этот выбор, в первом приближении, делается априори на основании имеющихся знаний относительно отклика. Например, если моделируется присутствие (1) и отсутствие (0) животных на некоторой изучаемой площади как функция нескольких факторов, то выбор прост: необходимо использовать биномиальное распределение. Однако это, вероятно, единственный сценарий, где ситуация столь очевидна.

Обычно, если это позволяет характер вариации переменной \(Y\), прибегают к аппроксимации счетных данных тем или иным непрерывным распределением - нормальным, гамма или Вейбулла, - что мы в конце концов и сделали с числом колец в раковинах морских ушек (рис. 8.4). Хорошему результату подгонки параметров модели и гарантированной неотрицательности модельных значений может способствовать преобразование исходных данных с помощью различных функций, таких как, логарифмирование или трансформация Бокса-Кокса (см. раздел 3.3).

Однако зачастую дискретность отклика оказывается столь очевидной (\(y_i = 0, 1, 2, \dots\)), что аппроксимация непрерывным распределением оказывается неудовлетворительной и это сильно влияет на адекватность регрессии с использованием МНК. Если счетные данные имеют тенденцию к гетерогенности (т.е. в большинстве случаев можно не встретить ни одного экземпляра, реже попадутся единичные особи, и лишь иногда их большие скопления) и фиксированный верхний предел у них отсутствует, то хорошим вариантом является аппроксимация наблюдений распределением Пуассона (Zuur et al., 2009).

Распределение Пуассона \(P(\lambda)\) имеет случайная величина \(Y\), отражающая количество событий, произошедших за некоторый промежуток времени, когда эти события независимы и происходят с постоянной интенсивностью \(\lambda\), \(\lambda \in (0, \infty)\). Предполагается, что среднее \(\mu = E(Y) = \lambda\) и дисперсия \(\text{Var}(Y) = \lambda\), а функция плотности вероятности \(p(k) = e^{-\lambda} \lambda^k/k!, \, \, k = 1, 2, \dots, \infty\), где \(k!\) - факториал от числа событий.

Пуассоновскую регрессию применяют, когда отклик является \(Y\) счетной переменной, имеющей такое распределение. Соответствующая модель имеет вид

\[\ln(\lambda) = \beta_0 + \sum_p \beta_j x_j,\]

где \(x_1, \dots, x_p\) - набор из \(p\) независимых переменных, \(\beta_0\) - математическое ожидание \(Y\) при равенстве нулю всех предикторов \(x_j\), \(\beta_j\) - коэффициенты независимых переменных.

Нередкими проблемами подгонки распределением Пуассона являются:

значительное по сравнению с теорией количество нулевых значений в выборке, сопровождающееся сильно разреженными таблицами данных;
эксцесс - избыток некоторых наблюдаемых значений по сравнению с ожидаемыми частотами;
наличие большой гетерогенности данных, вследствие чего оценка дисперсии начинает значимо превышать среднее, \(Var(Y) \gg \mu\) (overdispersion).

Если наблюдается отчетливая избыточная дисперсия (“перерассеяние”), то альтернативой распределению Пуассона для счетных данных является отрицательное биномиальное распределение.

*Отрицательное биномиальное распределение NB(r, p), также называемое распределением Паскаля, - это распределение дискретной случайной величины, которая отражает количество произошедших неудач в последовательности испытаний Бернулли с вероятностью успеха \(p\), проводимой до \(r\)-го успеха. Его обычно интерпретируют как смесь распределений гамма \(\Gamma(.)\) и Пуассона, т.е. функция плотности вероятности имеет вид:

\[f(y; \mu, \theta) = \frac{\Gamma(y + \theta)}{\Gamma(y)\theta !} \frac{\mu^y\theta^y}{\mu+\theta^{(y+\theta)}},\]

где \(\mu = E(Y)\) - среднее, а \(\theta\) - параметр формы распределения.

Включение в функцию распределения дополнительного параметра позволяет учесть превышение дисперсии над средним:

\[\text{Var}(Y) = \mu + \mu^2 / \theta.\]

При \(\theta \rightarrow \infty\) отрицательное биномиальное распределение сводится к распределению Пуассона (Agresti, 2007; Zeileis et al., 2008).

Обобщенная линейная модель для отрицательного биномиального распределения оценивает зависимость μ от совокупности объясняющих переменных с использованием функции связи (link function), как и в случае с лог-линейной моделью Пуассона. Принято считать, что параметр формы постоянен на всей области определения модели, что аналогично предположению о гомоскедастичности для моделей с нормальным распределением остатков.

Если аналитик колеблется в выборе между двумя конкурирующими статистическими моделями, то основанием для выбора может служить оценка согласия между наблюдаемыми данными и GLM с соответствующим теоретическим распределением. Рассмотрим эту задачу на примере двухлетнего подсчета числа амфибий, раздавленных автомобилями на 52 участках дорожной сети в южной части Португалии. Файл с данными RoadKills.txt можно скачать с полным комплектом данных к книге Zuur et al. (2009) на сайте http://www.highstat.com/book2.htm.

Само по себе распределение отклика TOT.N (числа погибших животных на каждом обследованном участке, экз.) трудно принять как пуассоновское (рис. 8.7):

RK <- read.table(file = "data/RoadKills.txt", header = TRUE, dec = ".")
y <- RK$TOT.N
library(vcd)
gf <- goodfit(table(y), type = "poisson", method = "ML") 
#  Визуализация подогнанных данных гистограммой 
plot(gf, ylab = "Частоты", xlab = "Число классов")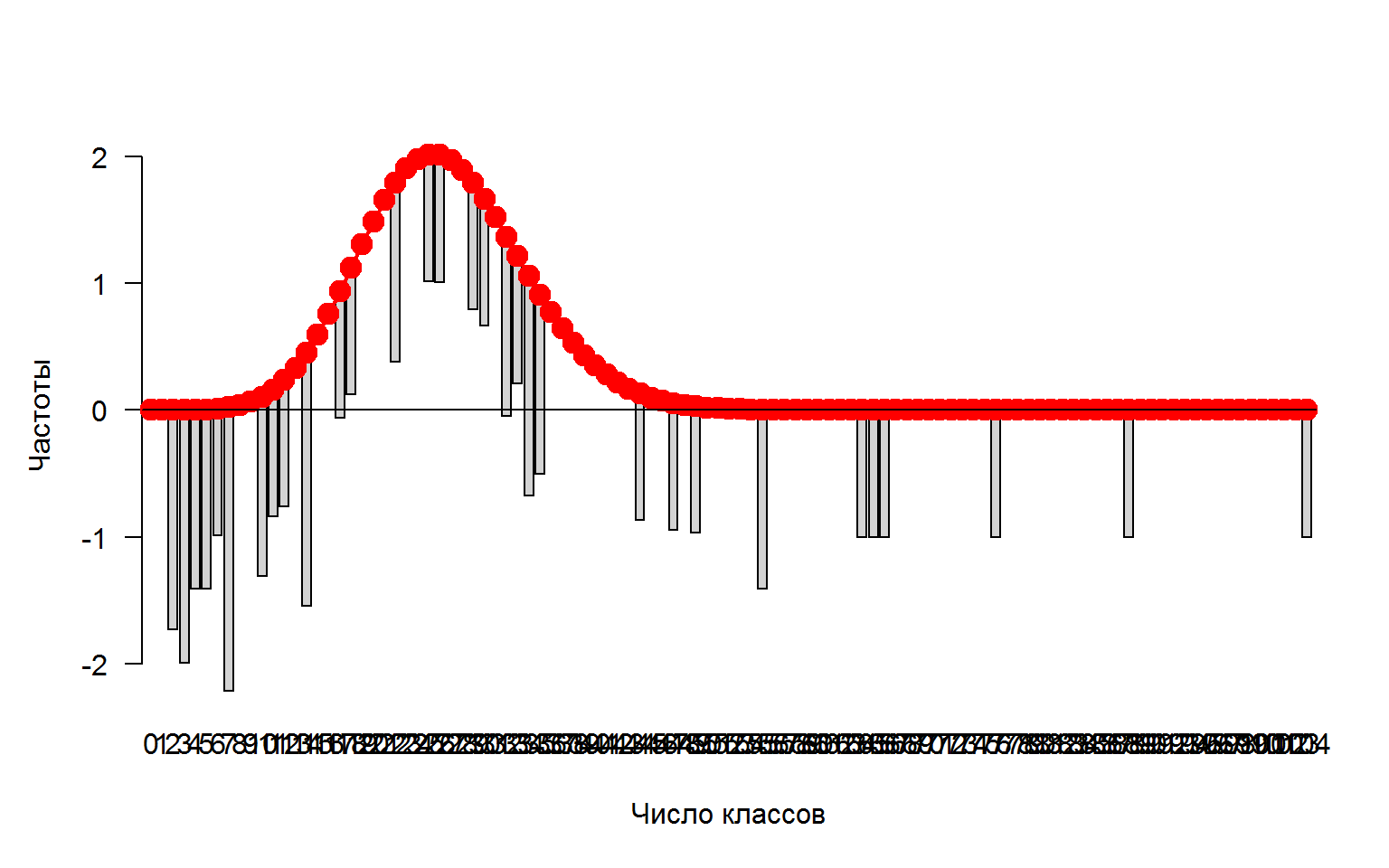

Рисунок 8.7: Гистограмма отклонений эмпирических частот от теоретических частот распределения Пуассона (красные кружки)

Модель регрессии Пуассона дает нам возможность объяснить эти отклонения за счет влияния внешних факторов. На первом этапе оценим общий вид моделируемых зависимостей, для чего применим одну независимую переменную - D.PARK (расстояние до заповедника), которая нам представляется наиболее экологически значимой:

M1 <-  glm(TOT.N ~ D.PARK, family =  poisson, data =  RK)
summary(M1)

## 
## Call:
## glm(formula = TOT.N ~ D.PARK, family = poisson, data = RK)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -8.1100  -1.6950  -0.4708   1.4206   7.3337  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  4.316e+00  4.322e-02   99.87   <2e-16 ***
## D.PARK      -1.059e-04  4.387e-06  -24.13   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 1071.4  on 51  degrees of freedom
## Residual deviance:  390.9  on 50  degrees of freedom
## AIC: 634.29
## 
## Number of Fisher Scoring iterations: 4

Была построена модель \(\log(\mu_i) = 4.13 - 0.0000106 \times \text{D.PARK}_i\), или в другой форме, \(\mu_i = \exp(4.13 - 0.0000106 \times \text{D.PARK}_i)\), где \(\mu_i\) - прогнозируемая величина пуассоновской частоты с учетом значения расстояния \(\text{D.PARK}_i\). Построим график полученной зависимости (рис. 8.8):

require(ggplot2)
MyData <- data.frame(D.PARK = seq(from = 0, to = 25000, by = 1000))
G <- predict(M1, newdata = MyData, type = "link", se = TRUE)
MyData$FIT <- exp(G$fit)
MyData$FSEUP <- exp(G$fit + 1.96*G$se.fit)
MyData$FSELOW <- exp(G$fit - 1.96*G$se.fit)
ggplot(MyData, aes(D.PARK, FIT)) +
    geom_ribbon(aes(ymin = FSEUP, ymax = FSELOW), 
                fill = 3, alpha = .25) + geom_line(colour = 3) +
    labs(x = "Расстояние до парка", y = "Убийства на дорогах") +
    geom_point(data = RK, aes(D.PARK, TOT.N) )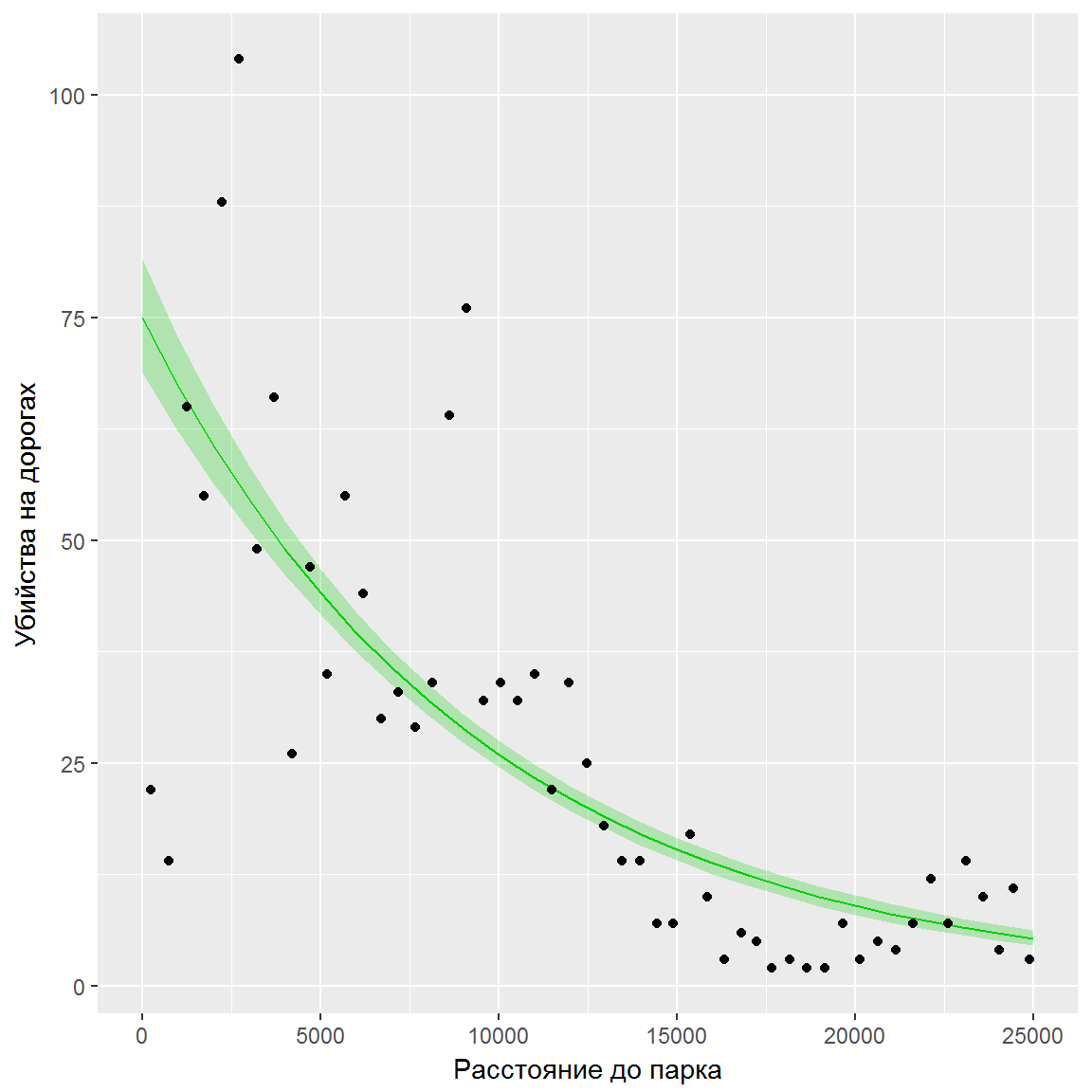

Рисунок 8.8: Зависимость числа раздавленных лягушек от расстояния до натурального лесного массива

Обращает на себя внимание очень узкая полоса 95%-го доверительного интервала относительно линии регрессии. Это обусловлено, возможно, как неверной спецификацией построенной модели, так и заниженной оценкой остаточной дисперсии.

Включим в модель дополнительные предикторы с целью повышения ее адекватности. В исходной таблице данных для этого имеется 18 полезных переменных-кандидатов. Выполним, однако, предварительно две операции - преобразование данных и удаление высоко коррелированных признаков.

Поскольку 8 переменных имеют размерность площади (га), а другие заданы длиной (расстоянием в м), то разумно привести их к единой функциональной форме и извлечь квадратный корень из значений первой группы признаков. Далее оценим степень мультиколлинеарности 18-мерного комплекса переменных и вычислим для каждого предиктора фактор инфляции дисперсии (Variance Inflation Factor, VIF).

library(car)
library(dplyr)
RK[, 7:14] <- sqrt(RK[, 7:14])
res <- sort(vif(glm(TOT.N ~ ., data = RK[, c(5, 7:23)], 
                    family =  poisson)))
print(res, 4)

##  D.WAT.RES D.WAT.COUR     D.PARK    WAT.RES   L.P.ROAD   L.D.ROAD 
##      1.876      2.315      2.630      2.667      4.323      4.538 
##     MONT.S    L.WAT.C      SHRUB      POLIC      URBAN     OPEN.L 
##      4.801      5.196      5.469      5.786      6.822     18.955 
##      OLIVE      L.SDI    N.PATCH     P.EDGE       MONT 
##     20.382     24.535     25.856     26.869     36.951

RK.11 <- select(RK, D.WAT.RES, D.WAT.COUR, WAT.RES,
                D.PARK, L.D.ROAD, L.P.ROAD, MONT.S, SHRUB,
                L.WAT.C, POLIC, URBAN)

Превышение VIF некоторого порогового значения (обычно это критическое значение принимается равным 5) свидетельствует о наличии проблемы мультиколлинеарности для \(X_j\). Удалим из таблицы данных 7 переменных с максимальными VIF.

Построим модель регрессии Пуассона с использованием предикторов, отобранных выше, и выполним процедуру пошаговой селекции исключений с включениями, пока не минимизируем значение AIC-критерия:

Y <- RK$TOT.N

M2 <-  glm(Y ~ ., family =  poisson, data =  RK.11)
summary(M2)

## 
## Call:
## glm(formula = Y ~ ., family = poisson, data = RK.11)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -5.1654  -1.4541   0.0377   1.6005   3.9850  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  3.765e+00  1.720e-01  21.890  < 2e-16 ***
## D.WAT.RES    4.006e-04  1.030e-04   3.891 9.97e-05 ***
## D.WAT.COUR   2.164e-04  1.607e-04   1.346 0.178218    
## WAT.RES      3.328e-01  7.078e-02   4.701 2.59e-06 ***
## D.PARK      -1.515e-04  6.550e-06 -23.131  < 2e-16 ***
## L.D.ROAD     1.484e-05  3.380e-05   0.439 0.660663    
## L.P.ROAD     4.450e-01  7.375e-02   6.034 1.60e-09 ***
## MONT.S       1.950e-01  3.661e-02   5.327 9.97e-08 ***
## SHRUB       -8.358e-01  1.284e-01  -6.509 7.54e-11 ***
## L.WAT.C      3.261e-01  4.554e-02   7.160 8.07e-13 ***
## POLIC       -1.533e-01  5.688e-02  -2.694 0.007054 ** 
## URBAN       -1.016e-01  2.636e-02  -3.855 0.000116 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 1071.44  on 51  degrees of freedom
## Residual deviance:  237.16  on 40  degrees of freedom
## AIC: 500.55
## 
## Number of Fisher Scoring iterations: 5

M3 <- step(M2, trace = 0)
summary(M3)

## 
## Call:
## glm(formula = Y ~ D.WAT.RES + WAT.RES + D.PARK + L.P.ROAD + MONT.S + 
##     SHRUB + L.WAT.C + POLIC + URBAN, family = poisson, data = RK.11)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -4.9834  -1.4447  -0.0584   1.4051   3.8822  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  3.904e+00  1.055e-01  37.015  < 2e-16 ***
## D.WAT.RES    3.516e-04  9.607e-05   3.660 0.000253 ***
## WAT.RES      3.120e-01  6.821e-02   4.574 4.79e-06 ***
## D.PARK      -1.491e-04  6.275e-06 -23.768  < 2e-16 ***
## L.P.ROAD     4.462e-01  6.468e-02   6.898 5.26e-12 ***
## MONT.S       2.005e-01  3.607e-02   5.558 2.73e-08 ***
## SHRUB       -8.151e-01  1.230e-01  -6.628 3.40e-11 ***
## L.WAT.C      2.917e-01  3.702e-02   7.879 3.31e-15 ***
## POLIC       -1.262e-01  4.325e-02  -2.918 0.003521 ** 
## URBAN       -1.070e-01  2.587e-02  -4.137 3.52e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 1071.44  on 51  degrees of freedom
## Residual deviance:  238.98  on 42  degrees of freedom
## AIC: 498.37
## 
## Number of Fisher Scoring iterations: 5

После исключения двух переменных в ходе пошаговой процедуры значение AIC-критерия несколько снизилось при статистически незначимом увеличении (c 237.2 до 239) остаточного девианса

\[D = 2 \sum_i \left( y_i \log \frac{y_i}{\mu_i} - (y_i - \mu_i)\right).\]

Напомним, что распределение разности девиансов асимптотически приближается к \(\chi^2\)-распределению с \(p1-p2\) степенями свободы

\[D_1 - D_2 \sim \chi^2_{p1-p2},\]

чем мы воспользовались, чтобы оценить статистическую значимость однородности ошибок двух регрессионных моделей с помощью команды anova(M2, M3, test = "Chi"). Та же функция для одной модели показывает, как уменьшается нуль-девианс при включении в модель последовательно каждого очередного предиктора:

anova(M3, test = "Chi")

## Analysis of Deviance Table
## 
## Model: poisson, link: log
## 
## Response: Y
## 
## Terms added sequentially (first to last)
## 
## 
##           Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
## NULL                         51    1071.44              
## D.WAT.RES  1   109.55        50     961.89 < 2.2e-16 ***
## WAT.RES    1     0.28        49     961.61 0.5947268    
## D.PARK     1   595.60        48     366.01 < 2.2e-16 ***
## L.P.ROAD   1     7.17        47     358.84 0.0074114 ** 
## MONT.S     1    16.35        46     342.49 5.272e-05 ***
## SHRUB      1    20.79        45     321.71 5.138e-06 ***
## L.WAT.C    1    51.96        44     269.75 5.666e-13 ***
## POLIC      1    12.80        43     256.95 0.0003475 ***
## URBAN      1    17.97        42     238.98 2.240e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Очевидно, что наибольший вклад в снижение ошибки модели вносят расстояния до лесного массива, реки или другого водного резервуара (D.PARK, D.WAT.RES, L.WAT.C), в меньшей мере это относится к наличию кустарников (SHRUB), поликультурных насаждений (POLIC) или урбанизированных территорий (URBAN), а доля девианса, связанного с площадью водного резервуара (WAT.RES), не отличается от нуля.

Однако следует задаться вопросом, насколько точно была оценена нами дисперсия аппроксимирующего распределения. Поскольку остаточный девианс имеет \(\chi^2\)-распределение с \((n - p)\) степенями свободы, то одним из признаков избыточной дисперсии является значение \(\phi = D/(n-p)\). Если это отношение приблизительно равно 1, то можно благополучно предположить, что избыточно дисперсии нет. В рассматриваемом примере \(\phi = 239/42 = 5.69\) и опасность недооценки дисперсии существует.

Мы можем компенсировать возможную избыточную дисперсию, приняв квази-распределение Пуассона и задав в функции glm() параметр family = quasipoisson. Для этого типа распределения среднее и дисперсия для \(Y\) будет равно \(E(Y) = \mu\) и \(\text{Var} = \phi \times \mu\):

M4 <- glm(Y ~ D.WAT.RES + WAT.RES + D.PARK + L.P.ROAD +
              MONT.S + SHRUB + L.WAT.C + POLIC + URBAN, 
          family = quasipoisson, data =  RK.11)
summary(M4)

## 
## Call:
## glm(formula = Y ~ D.WAT.RES + WAT.RES + D.PARK + L.P.ROAD + MONT.S + 
##     SHRUB + L.WAT.C + POLIC + URBAN, family = quasipoisson, data = RK.11)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -4.9834  -1.4447  -0.0584   1.4051   3.8822  
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.904e+00  2.401e-01  16.261  < 2e-16 ***
## D.WAT.RES    3.516e-04  2.187e-04   1.608  0.11539    
## WAT.RES      3.120e-01  1.553e-01   2.009  0.05095 .  
## D.PARK      -1.491e-04  1.428e-05 -10.442 3.04e-13 ***
## L.P.ROAD     4.462e-01  1.472e-01   3.031  0.00417 ** 
## MONT.S       2.005e-01  8.210e-02   2.442  0.01891 *  
## SHRUB       -8.151e-01  2.799e-01  -2.912  0.00573 ** 
## L.WAT.C      2.917e-01  8.426e-02   3.461  0.00125 ** 
## POLIC       -1.262e-01  9.845e-02  -1.282  0.20688    
## URBAN       -1.070e-01  5.890e-02  -1.818  0.07627 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for quasipoisson family taken to be 5.181428)
## 
##     Null deviance: 1071.44  on 51  degrees of freedom
## Residual deviance:  238.98  on 42  degrees of freedom
## AIC: NA
## 
## Number of Fisher Scoring iterations: 5

Другой формой команды anova() является функция drop1(), которая поочередно удаляет из модели по одной объясняющей переменной и каждый раз пересчитывает значение остаточного девианса. Значимость различий отдельных моделей оценивается по \(\chi^2\)-критерию.

drop1(M4, test = "Chi")

## Single term deletions
## 
## Model:
## Y ~ D.WAT.RES + WAT.RES + D.PARK + L.P.ROAD + MONT.S + SHRUB + 
##     L.WAT.C + POLIC + URBAN
##           Df Deviance scaled dev.  Pr(>Chi)    
## <none>         238.98                          
## D.WAT.RES  1   252.26       2.564 0.1092996    
## WAT.RES    1   258.82       3.829 0.0503756 .  
## D.PARK     1   888.32     125.321 < 2.2e-16 ***
## L.P.ROAD   1   284.12       8.712 0.0031606 ** 
## MONT.S     1   268.17       5.633 0.0176229 *  
## SHRUB      1   285.09       8.899 0.0028526 ** 
## L.WAT.C    1   301.24      12.017 0.0005271 ***
## POLIC      1   247.95       1.731 0.1882444    
## URBAN      1   256.95       3.469 0.0625355 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Отметим, что в результате применения квази-пуассоновского распределения при наличии избыточной дисперсии мы получаем следующую коррекцию модели Пуассона:

значения коэффициентов модели и оценки ее девианса не меняются;
\(р\)-величины коэффициентов увеличиваются и некоторые параметры модели оцениваются уже как статистически незначимые;
величина AIC-критерия рассчитана быть не может.

Заметим также, что ширина доверительного интервала модели на рис. 8.8 должна быть увеличена в \(\phi = 7.63\) раза.

Мы получили регрессионную модель, достаточно убедительную с экологической точки зрения и позволяющую ранжировать и интерпретировать степень влияния отдельных предикторов. Однако насколько она хороша для прогнозирования на новых данных? Загрузим пакет caret и проведем отбор информативного комплекса переменных методом RFE (Recursive feature selection - см. раздел 4.1):

library(caret)
glmFuncs <- lmFuncs
glmFuncs$fit <- function(x, y, first, last, ...) { 
    tmp <- as.data.frame(x)
    tmp$y <- y 
    glm(y ~ ., data = tmp, family = quasipoisson(link = 'log'))
}
set.seed(13)
ctrl <- rfeControl(functions = glmFuncs, method = "cv", 
                   verbose = FALSE, returnResamp = "final")
lmProfileF <- rfe(x = RK.11, y = RK$TOT.N, sizes = 1:10,
                  rfeControl = ctrl)

Проверим справедливость сделанного выбора с помощью функции train():

train(TOT.N ~ D.PARK, data = RK, method = 'glm', 
      family = quasipoisson, trControl = 
          trainControl(method = "cv", verboseIter = FALSE))

## Generalized Linear Model 
## 
## 52 samples
##  1 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 47, 47, 48, 47, 46, 46, ... 
## Resampling results:
## 
##   RMSE      Rsquared 
##   15.95588  0.7753695
## 
##

train(TOT.N ~ D.WAT.RES + WAT.RES + D.PARK + L.P.ROAD +
          MONT.S + SHRUB + L.WAT.C + POLIC + URBAN, data = RK,
      method='glm', family = quasipoisson,
      trControl = trainControl(method = "cv", verboseIter = FALSE))

## Generalized Linear Model 
## 
## 52 samples
##  9 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 47, 46, 45, 45, 49, 48, ... 
## Resampling results:
## 
##   RMSE      Rsquared 
##   18.99993  0.5742747
## 
##

Тестирование показало, что модель с 1 предиктором при перекрестной проверке дает меньшую ошибку, чем множественная регрессия на основе 9 параметров.

Выполним теперь построение модели на основе отрицательного биномиального распределения (NB), для чего воспользуемся функцией glm.nb() из пакета MASS:

library(MASS)
M5 <-  glm.nb(Y ~ .,  data = RK.11)
summary(M5)

## 
## Call:
## glm.nb(formula = Y ~ ., data = RK.11, init.theta = 5.539729346, 
##     link = log)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -2.49027  -0.78494  -0.05133   0.68202   1.44678  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  3.821e+00  3.528e-01  10.830   <2e-16 ***
## D.WAT.RES    4.469e-04  2.411e-04   1.854   0.0638 .  
## D.WAT.COUR   2.761e-04  3.537e-04   0.781   0.4350    
## WAT.RES      2.778e-01  1.736e-01   1.600   0.1096    
## D.PARK      -1.502e-04  1.472e-05 -10.203   <2e-16 ***
## L.D.ROAD     1.434e-05  7.091e-05   0.202   0.8397    
## L.P.ROAD     3.528e-01  1.708e-01   2.066   0.0389 *  
## MONT.S       1.831e-01  8.950e-02   2.045   0.0408 *  
## SHRUB       -6.939e-01  3.046e-01  -2.278   0.0227 *  
## L.WAT.C      2.349e-01  1.029e-01   2.284   0.0224 *  
## POLIC       -1.297e-01  1.499e-01  -0.866   0.3866    
## URBAN       -2.917e-02  6.651e-02  -0.439   0.6610    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(5.5397) family taken to be 1)
## 
##     Null deviance: 214.316  on 51  degrees of freedom
## Residual deviance:  54.764  on 40  degrees of freedom
## AIC: 396.92
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  5.54 
##           Std. Err.:  1.50 
## 
##  2 x log-likelihood:  -370.919

M6 <- step(M5, trace = 0)
summary(M6)

## 
## Call:
## glm.nb(formula = Y ~ D.WAT.RES + WAT.RES + D.PARK + L.P.ROAD + 
##     MONT.S + SHRUB + L.WAT.C, data = RK.11, init.theta = 5.204690159, 
##     link = log)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -2.59068  -0.82198  -0.02681   0.67624   1.29964  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  3.943e+00  2.435e-01  16.194   <2e-16 ***
## D.WAT.RES    4.478e-04  2.217e-04   2.020   0.0434 *  
## WAT.RES      2.546e-01  1.719e-01   1.482   0.1385    
## D.PARK      -1.447e-04  1.385e-05 -10.449   <2e-16 ***
## L.P.ROAD     2.820e-01  1.419e-01   1.987   0.0469 *  
## MONT.S       2.024e-01  8.882e-02   2.279   0.0227 *  
## SHRUB       -6.690e-01  3.074e-01  -2.176   0.0296 *  
## L.WAT.C      1.644e-01  8.351e-02   1.968   0.0491 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(5.2047) family taken to be 1)
## 
##     Null deviance: 204.391  on 51  degrees of freedom
## Residual deviance:  54.054  on 44  degrees of freedom
## AIC: 390.57
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  5.20 
##           Std. Err.:  1.37 
## 
##  2 x log-likelihood:  -372.571

В дополнение к обычному набору показателей в протокол включены оценка дисперсии и параметр распределения Theta, обозначенный выше как \(\theta\). В отношении построенных моделей NB можно также выполнить анализ девиансов, как это мы делали выше на примере пуассоновской регрессии. При сравнении моделей, построенных для разных распределений, необходимо использовать величины логарифмов функции правдоподобия или значения AIC-критерия: значение последнего для NB-модели AIC = 390.57 существенно меньше, чем для оптимальной модели регрессии Пуассона AIC = 498.37.

Выполним в заключение тестирование в режиме перекрестной проверки моделей отрицательного биномиального распределения с одним и семью предикторами соответственно:

train(TOT.N ~ D.PARK, data = RK, method = 'glm.nb', 
      trControl = trainControl(method = "cv", verboseIter = FALSE))

## Negative Binomial Generalized Linear Model 
## 
## 52 samples
##  1 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 47, 48, 46, 47, 46, 46, ... 
## Resampling results across tuning parameters:
## 
##   link      RMSE      Rsquared 
##   identity       NaN        NaN
##   log       31.55278  0.6871591
##   sqrt      29.85382  0.6871591
## 
## RMSE was used to select the optimal model using  the smallest value.
## The final value used for the model was link = sqrt.

train(TOT.N ~ D.WAT.RES + WAT.RES + D.PARK + L.P.ROAD + 
          MONT.S + SHRUB + L.WAT.C, data = RK, method = 'glm.nb', 
      trControl = trainControl(method = "cv", verboseIter = FALSE))

## Negative Binomial Generalized Linear Model 
## 
## 52 samples
##  7 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 47, 48, 48, 46, 46, 47, ... 
## Resampling results across tuning parameters:
## 
##   link      RMSE      Rsquared 
##   identity       NaN        NaN
##   log       31.69848  0.7108295
##   sqrt      29.83198  0.7294065
## 
## RMSE was used to select the optimal model using  the smallest value.
## The final value used for the model was link = sqrt.

В этом случае обе модели показали весьма близкие результаты и окончательный вывод зависит от решения аналитика. Заметим, что функция train() попутно сравнила два вида функции связи (link) и более точным оказалось использование квадратного корня.