Классификация, регрессия и другие алгоритмы Data Mining с использованием R

3.5 Функция `train()` из пакета `caret`

Как подчеркивалось ранее в разделе 3.1, пакет caret был разработан как эффективная надстройка, позволяющая унифицировать и интегрировать использование множества различных функций и методов построения моделей классификации и регрессии, представленных в других пакетах R. При этом происходит всестороннее тестирование и оптимизация настраиваемых коэффициентов и гиперпараметров моделей. Эта разработанная единая технология реализована в функции train(), использующей полуавтоматические интеллектуальные подходы и универсальные критерии качества с применением алгоритмов ресэмплинга.

Перед выполнением подгонки модели с помощью функции train() необходимо задать соответствующий алгоритм и всю совокупность условий процесса оптимизации параметров модели, для чего при помощи функции trainControl() создается специальный объект. Вызов этой функции со значениями, принимаемыми по умолчанию, имеет следующий вид:

trainControl(method = "boot", 
             number = ifelse(grepl("cv", method), 10, 25), p = 0.75,
             repeats = ifelse(grepl("cv", method), 1, number),
             search = "grid", initialWindow = NULL, horizon = 1,
             fixedWindow = TRUE, verboseIter = FALSE, returnData = TRUE,
             returnResamp = "final", savePredictions = FALSE, 
             classProbs = FALSE, summaryFunction = defaultSummary,
             selectionFunction = "best", seeds = NA,
             preProcOptions = list(thresh = 0.95, ICAcomp = 3, k = 5),
             sampling = NULL, index = NULL, indexOut = NULL,
             timingSamps = 0, predictionBounds = rep(FALSE, 2), 
             adaptive = list(min = 5, alpha = 0.05, method = "gls", complete = TRUE),
             trim = FALSE, allowParallel = TRUE)

Остановимся на описании наиболее важных аргументов этой функции:

method - метод ресэмплинга: "boot", "boot632", "cv", "repeatedcv", "LOOCV", "LGOCV" (для повторяющихся разбиений на обучающую и проверочную выборки), "none" (исследуется только модель на обучающей выборке), "oob" (для таких алгоритмов, как случайный лес, бэггинг деревьев и др.), "adaptive_cv", "adaptive_boot" или "adaptive_LGOCV";
number - задает число итераций ресэмплинга, в частности, число блоков (folds) при перекрестной проверке;
repeats - число повторностей (только для k-кратной перекрестной проверки);
p - доля обучающей выборки от общего объема при выполнении перекрестной проверки;
verboseIter - TRUE означает, что в ходе вычислений caret будет показывать, на каком этапе они находятся (это удобно для оценки оставшегося времени вычислений, которое часто бывает очень большим);
search - способ перебора параметров модели (по сетке - "grid", или случайным назначением - "random");
returnResamp и savePredictions - определяют условия сохранения результатов выполнения ресэмплинга и прогнозируемых значений, т.е. "none", только для итоговой модели "final" или все "all";
classProbs - TRUE означает, что в процессе вычислений алгоритм будет сохранять данные о вероятностях попадания объекта в каждый класс, а не только конечные метки класса;
summaryFunction - определяет функцию, которая вычисляет метрику качества модели при ресэмплинге;
selectionFunction - определяет функцию выбора оптимального значения настраиваемого параметра;
preProcOptions - список опций, который передается функции предобработки данных preProcess().

Например, при создании объекта ctrl <- trainControl(method = "repeatedcv", number = 10, repeats = 10) параметры перекрестной проверки будут иметь следующий смысл:

method = "repeatedcv" означает, что будет использоваться повторная перекрестная проверка (также возможна перекрестная проверка, leave-one-out проверка, и т.д.);
number = 10 означает, что в процессе перекрестной проверки выборку надо разбивать на 10 равных частей;
repeats = 10 означает, что повторная перекрестная проверка должна быть запущена 10 раз.

Теперь перейдем непосредственно к описанию функции train(), которая имеет следующий формат вызова:

train(x, y, 
      method = "rf", 
      preProcess = NULL, 
      weights = NULL,
      metric = ifelse(is.factor(y), "Accuracy", "RMSE"), 
      maximize = ifelse(metric %in% c("RMSE", "logLoss"), FALSE, TRUE), 
      trControl = trainControl(),
      tuneGrid = NULL,
      tuneLength = 3)

Исходные данные задаются, как всегда, либо матрицей предикторов x и вектором отклика y, либо объектом formula с указанием таблицы данных data. Следующий аргумент - method - это, в сущности, название модели классификации или регрессии, которую необходимо построить и протестировать. Если выполнить команду names(getModelInfo()), то можно увидеть список из 233 доступных методов (это количество постоянно расширяется). Тот же список, но с различными возможностями поиска и сортировки можно посмотреть по следующим адресам в Интернете:

http://topepo.github.io/caret/modelList.html или
http://topepo.github.io/caret/bytag.html

Можно просмотреть названия всех моделей, которые имеют, например, отношение к линейной регрессии:

library(caret)
ls(getModelInfo(model = "lm"))

##  [1] "bayesglm"       "elm"            "glm"            "glm.nb"        
##  [5] "glmboost"       "glmnet"         "glmnet_h2o"     "glmStepAIC"    
##  [9] "lm"             "lmStepAIC"      "plsRglm"        "rlm"           
## [13] "vglmAdjCat"     "vglmContRatio"  "vglmCumulative"

С каждым методом связан набор гиперпараметров, подлежащих оптимизации. Можно убедиться в том, что простая линейная регрессия (method = "lm") не имеет параметров для настройки:

modelLookup("lm")

##   model parameter     label forReg forClass probModel
## 1    lm intercept intercept   TRUE    FALSE     FALSE

В свою очередь, деревья решений rpart, которые мы рассмотрим позднее, имеют один параметр для настройки - Complexity Parameter (аббревиатура - cp):

modelLookup("rpart")

##   model parameter                label forReg forClass probModel
## 1 rpart        cp Complexity Parameter   TRUE     TRUE      TRUE

Из сообщений функции modelLookup() можно также увидеть, что линейная регрессия не используется для классификации (forClass= FALSE), тогда как rpart (от “Recursive Partitioning and Regression Trees”) можно применять как для построения деревьев регрессии, так и классификации. В последнем случае модель осуществляет не только предсказание класса, но и оценивает апостериорные вероятности (probModel = TRUE).

Метод перекрестной проверки, заданный объектом trControl = trainControl(), обеспечивает сканирование настраиваемых параметров и оценку эффективности модели на каждой итерации по определенным критериям качества. При построении каждой частной модели предварительно осуществляется предобработка данных с использованием методов, перечисленных в preProcess (и с учетом опций preProcOptions объекта trControl).

По умолчанию аргумент metric использует в качестве критерия качества точность предсказания ("Accuracy") в случае классификации (см. пример, рассмотренный в разделе 3.3) и корень из среднеквадратичного отклонения прогнозируемых значений от наблюдаемых ("RMSE") для регрессии. Логический аргумент maximize уточняет, должен ли этот критерий быть максимизирован или минимизирован. Другие значения metric вместе с различными значениями аргументов summaryFunction и selectionFunction объекта trControl обеспечивают широкие возможности пользовательского назначения метрик для оценки эффективности моделей.

Количество перебираемых значений настраиваемого параметра задается аргументом tuneLength. Например, чтобы задать 30 повторов оценки параметра cр модели rpart вместо исходных трех, необходимо указать tuneLength = 30. Другой вариант - определить последовательность этих значений в списке, задающем сетку: например, tuneGrid = expand.grid(.cp = 0.5^(1:10)), если заранее известен диапазон, к которому принадлежит оптимизируемое значение.

После завершения перебора всех положенных комбинаций параметров модели создается объект класса train, соответствующие элементы которого можно извлечь с помощью суффикса $:

ls(mytrain)

Приведем краткий пример на тему подбора полиномиальной регрессии для описания зависимости электрического сопротивления (Ом) мякоти фруктов киви от процентного содержания в ней сока, который подробно разбирался нами в разделе 2.1. Позже (раздел 2.2) мы показали, как найти оптимальную степень полинома $d = 4$ с использованием написанной нами функции скользящего контроля.

К сожалению, функция train() селекцию предикторов для метода "lm" не выполняет и оптимальную степень полинома не настраивает. Но мы можем выполнить любую перекрестную проверку для оценки динамики изменения критериев качества модели - среднеквадратичной ошибки RMSE и среднего коэффициента детерминации RSquared (рис. 3.8):

library(DAAG)
data("fruitohms")
set.seed(123) 
max.poly <- 7
degree <- 1:max.poly
RSquared <- rep(0, max.poly)
RMSE <- rep(0, max.poly)

# Выполним 10-кратную кросс-проверку с 10 повторностями
fitControl <- trainControl(method = "repeatedcv",
                           number = 10, repeats = 10)

# Тестируем модель для различных степеней:
for (d in degree)  {
    f <- bquote(juice ~ poly(ohms, .(d)))
    LinearRegressor <- train(as.formula(f),
                             data = fruitohms,
                             method = "lm", trControl = fitControl)
    RSquared[d] <- LinearRegressor$results$Rsquared
    RMSE[d] <- LinearRegressor$results$RMSE
}

library(ggplot2)
library(gridExtra)
Degree.RegParams <- data.frame(degree, RSquared, RMSE)
a <- ggplot(aes(x = degree, y = RSquared),
       data = Degree.RegParams) + geom_line()
b <- ggplot(aes(x = degree, y = RMSE),
       data = Degree.RegParams) + geom_line()
grid.arrange(a, b, ncol = 2)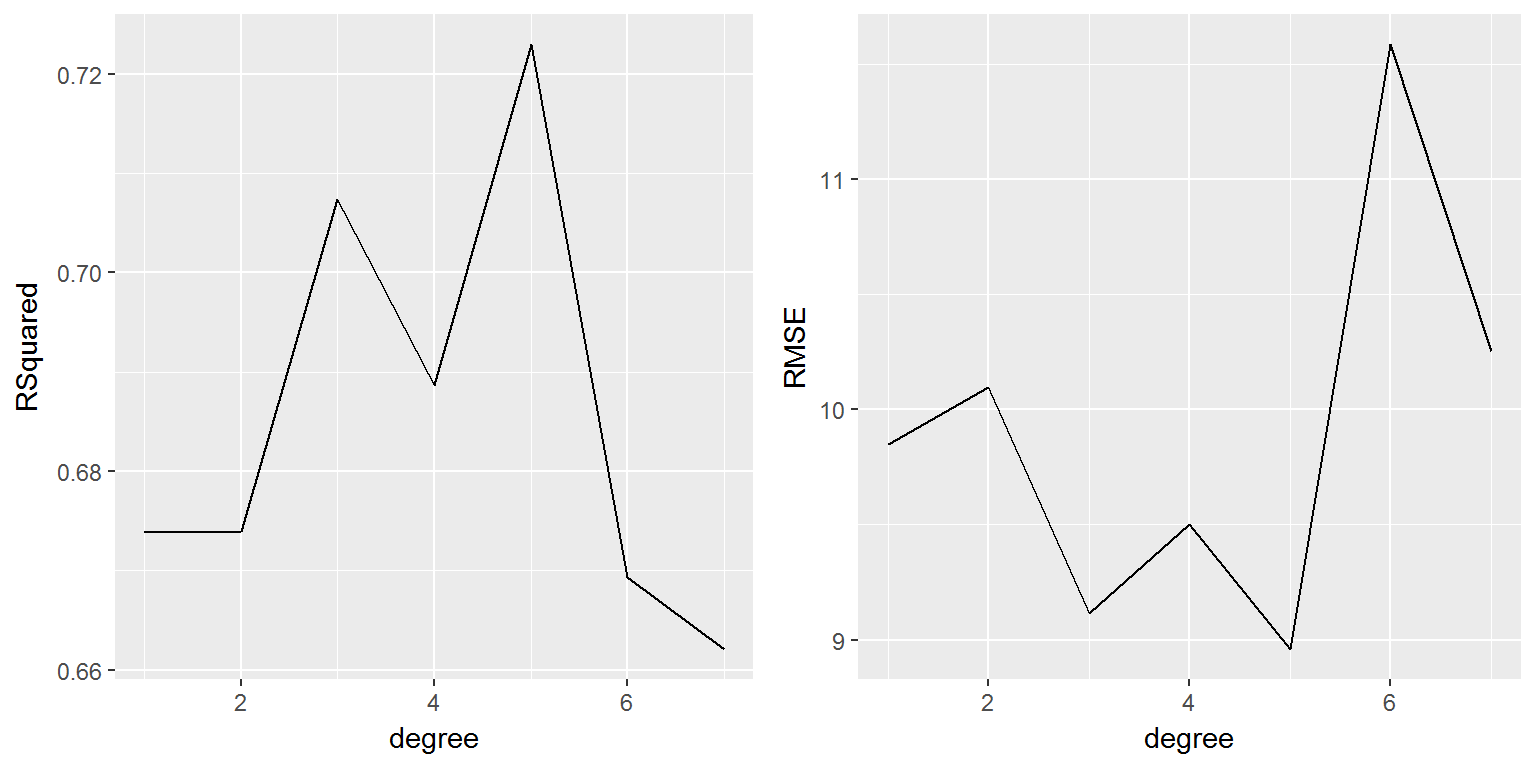

Рисунок 3.8: Поиск степени функции полиномиальной регрессии с использованием функции train()

В отличие от ранее проведенных расчетов, минимум ошибки и максимум коэффициента детерминации имеют место при $d = 5$.

Если не задавать непосредственно объект trControl, то по умолчанию вместо кросс-проверки функция train() осуществляет бутстреп критериев качества подгонки RMSE и RSquared:

Poly5 <- train(ohms ~ poly(juice,5), data = fruitohms, method = "lm")
summary(Poly5$finalModel)

## 
## Call:
## lm(formula = .outcome ~ ., data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3363.7  -508.9   -35.8   459.7  2797.7 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         4360.0       83.2  52.406  < 2e-16 ***
## `poly(juice, 5)1` -16750.2      941.3 -17.796  < 2e-16 ***
## `poly(juice, 5)2`   4750.6      941.3   5.047 1.59e-06 ***
## `poly(juice, 5)3`   3945.6      941.3   4.192 5.27e-05 ***
## `poly(juice, 5)4`  -3371.2      941.3  -3.582 0.000492 ***
## `poly(juice, 5)5`   1057.3      941.3   1.123 0.263509    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 941.3 on 122 degrees of freedom
## Multiple R-squared:  0.7539, Adjusted R-squared:  0.7439 
## F-statistic: 74.76 on 5 and 122 DF,  p-value: < 2.2e-16

summary(lm(ohms ~ poly(juice, 5), data = fruitohms))

## 
## Call:
## lm(formula = ohms ~ poly(juice, 5), data = fruitohms)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3363.7  -508.9   -35.8   459.7  2797.7 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)       4360.0       83.2  52.406  < 2e-16 ***
## poly(juice, 5)1 -16750.2      941.3 -17.796  < 2e-16 ***
## poly(juice, 5)2   4750.6      941.3   5.047 1.59e-06 ***
## poly(juice, 5)3   3945.6      941.3   4.192 5.27e-05 ***
## poly(juice, 5)4  -3371.2      941.3  -3.582 0.000492 ***
## poly(juice, 5)5   1057.3      941.3   1.123 0.263509    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 941.3 on 122 degrees of freedom
## Multiple R-squared:  0.7539, Adjusted R-squared:  0.7439 
## F-statistic: 74.76 on 5 and 122 DF,  p-value: < 2.2e-16

Poly5

## Linear Regression 
## 
## 128 samples
##   1 predictor
## 
## No pre-processing
## Resampling: Bootstrapped (25 reps) 
## Summary of sample sizes: 128, 128, 128, 128, 128, 128, ... 
## Resampling results:
## 
##   RMSE      Rsquared 
##   981.9573  0.7238476
## 
## Tuning parameter 'intercept' was held constant at a value of TRUE
##

Мы получили в точности те же коэффициенты модели, что и при использовании базовой функции lm(), но для критериев RMSE и RSquared были найдены стандартные ошибки, позволяющие рассчитать доверительные интервалы этих статистик. Оценка проводилась по результатам 25 бутстреп-итераций, выполняемых функцией train() по умолчанию. Обратите внимание, что несмещенное бутстреп-значение коэффициента детерминации (0.734) несколько меньше, чем рассчитанное функцией summary() для финальной модели (0.754). В заключении приведем сокращенную таблицу доступных в train() моделей с указанием наименований их параметров. С нашей точки зрения, таблица полезна также тем, что является своеобразным путеводителем по пакетам R и реализованным в них статистическим методам. В последующих разделах мы приведем описание большинства перечисленных методов и продемонстрируем процесс оптимизации их параметров с помощью функции train().

Список методов, моделей и их параметров, оптимизируемых с использованием функции train()

Модели	Значение method	Пакет	Оптимизируемые параметры
Деревья на основе рекурсивного деления (recursive partitioning)	rpart	rpart	maxdepth
	ctree	party	mincriterion
Бустинг деревьев (boosted trees)	gbm	gbm	interaction.depth, n.trees, shrinkage
	blackboost	mboost	maxdepth, mstop
	ada	ada	maxdepth, iter, nu
Другие модели бустинга (other boosted models)	glmboost	mboost	mstop
	gamboost	mboost	mstop
	logitboost	caTools	nIter
Случайный лес (random forest)	rf	randomForest	mtry
	cforest	party	mtry
Бэггинг-деревья (bagged trees)	treebag	ipred
Нейронные сети (neural networks)	nnet	nnet	decay, size
Частные наименьшие квадраты (partial least squares)	pls	pls, caret	ncomp
Машина опорных векторов с RBF ядром (support vector machines RBF kernel)	svmRadial	kernlab	sigma, C
Машина опорных векторов с полиномиальным ядром (support vector machines polynomial kernel)	svmPoly	kernlab	scale, degree, C
Гауссовы процессы с RBF ядром (Gaussian processes with RBF kernel)	gaussprRadial	kernlab	sigma
Гауссовы процессы с полиномиальным ядром (Gaussian processes with polynomial kernel)	gaussprPoly	kernlab	scale, degree
Линейные модели наименьших квадратов (linear least squares)	lm	stats
Многомерные адаптивные регрессионные сплайны (multivariate adaptive regression splines MARS)	earth, mars	earth	degree, nprune
Бэггинг-сплайны MARS (bagged MARS)	bagEarth	caret, earth	degree, nprune
Эластичные сети (elastic net)	enet	elasticnet	lambda, fraction
Лассо (the lasso)	lasso	elasticnet	fraction
Машины релевантных векторов с RBF ядром (relevance vector machines RBF kernel)	rvmRadial	kernlab	sigma
Машины релевантных векторов с полиномиальным ядром (relevance vector machines polynomial kernel	rvmPoly	kernlab	scale, degree
Линейный дискриминантный анализ (linear discriminant analysis)	lda	MASS
Пошаговый диагональный дискриминантный анализ (stepwise diagonal discriminant analysis)	sddaLDA, sddaQDA	SDDA
Логистическая регрессия для двух или более классов (logistic/multinomial regression)	multinom	nnet	decay
Регуляризованный дискриминантный анализ (Regularized discriminant analysis)	rda	klaR	lambda, gamma
Гибкий дискриминантный анализ (Flexible discriminant analysis FDA)	fda	mda, earth	degree, nprune
FDA на основе бэггинга (bagged FDA)	bagFDA	caret, earth	degree, nprune
Машины опорных векторов на основе метода наименьших квадратов c RBF ядром (least squares support vector machines RBF kernel)	lssvmRadial	kernlab	sigma
Метод k-ближайших соседей (k nearest neighbors)	knnЗ	caret	k
Разделение по центроидам (nearest shrunken centroids)	pam	pamr	threshold
Наивный байесовский классификатор (naive Bayes)	nb	klaR	usekernel
Обобщенный метод частных наименьших квадратов (Generalized partial least squares)	gpls	gpls	K.prov
Сети с квантованием обучающего вектора (learned vector quantization)	lvq	class	k

3.5 Функция train() из пакета caret

3.5 Функция `train()` из пакета `caret`