2.5 Многомерный статистический анализ данных
Взаимосвязь между двумя комплексами переменных может быть установлена в ходе канонического анализа (от греческого \(\kappa \alpha \nu \omega \nu\)). В математике, канонической формой называется самая простая и универсальная форма, к который определенные функции, отношения, или выражения могут быть приведены без потери общности. Наиболее распространенными формами канонической ординации, основанной на приведении к собственным значениям и собственным векторам, являются анализ избыточности RDA (redundancy analysis) и линейный дискриминантный анализ LDA (linear discriminant analysis).
Анализ избыточности (Джонгман и др., 1999; Legendre, Legendre, 2012) является непосредственным расширением идей множественной регрессии на моделирование данных с многомерным откликом. Анализ асимметричен, т.е., если \(\mathbf{Y} (n \times m)\) - таблица зависимых и \(X(n \times q)\) - таблица объясняющих переменных, то есть \(m \neq q\). RDA выполняется в три этапа:
- Оцениваются коэффициенты \(\mathbf В\) модели множественной линейной регрессии \(\mathbf Y\) на \(\mathbf X\) и формируется матрица прогнозируемых значений: \(\mathbf{\hat{Y}} = \mathbf{XB} = \mathbf{fX[X'X]^{-1}X'Y}\);
- Вычисляется матрица канонических коэффициентов \(\mathbf{S = BU_с}\) размерностью \(m \times q\), которая рассчитывается на основе собственных векторов \(\mathbf{U_с}\), взвешивающих влияние объясняющих переменных (constrained eigenvalues).
- Рассчитывается ковариационная матрица \(\mathbf{C_{y|x}}\) на основе значений \(\mathbf{\hat{Y}}\), выполняется анализ главных компонент: \(\mathbf{ (C_{y|x} - \lambda_k I)u_k = 0}\), где \(\mathbf{C_{y|x} = C_{YX}C_{XX}^{-1}C^T_{YX}}\) и обычным путем вычисляется матрица нагрузок на основе \(k\) собственных векторов, не связанных с объясняющими переменными Х (unconstrained eigenvalues).
Для примера, описанного в разделе 2.4, матрица \(\mathbf Х\) сводится к вектору типа стекла FAC, и анализ избыточности приводит к следующим результатам:
FAC <- as.factor(ifelse(DGlass$Class == 2, 2, 1))
Y <- as.data.frame(DGlass[, 1:9])
mod.rda <- vegan::rda(Y ~ FAC)
head(summary(mod.rda))##
## Call:
## rda(formula = Y ~ FAC)
##
## Partitioning of variance:
## Inertia Proportion
## Total 3.6563 1.00000
## Constrained 0.1183 0.03236
## Unconstrained 3.5380 0.96764
##
## Eigenvalues, and their contribution to the variance
##
## Importance of components:
## RDA1 PC1 PC2 PC3 PC4 PC5
## Eigenvalue 0.11833 2.5441 0.5584 0.21014 0.15944 0.04155
## Proportion Explained 0.03236 0.6958 0.1527 0.05747 0.04361 0.01136
## Cumulative Proportion 0.03236 0.7282 0.8809 0.93837 0.98197 0.99334
## PC6 PC7 PC8 PC9
## Eigenvalue 0.01401 0.008824 0.001533 6.816e-07
## Proportion Explained 0.00383 0.002410 0.000420 0.000e+00
## Cumulative Proportion 0.99717 0.999580 1.000000 1.000e+00
##
## Accumulated constrained eigenvalues
## Importance of components:
## RDA1
## Eigenvalue 0.1183
## Proportion Explained 1.0000
## Cumulative Proportion 1.0000
##
## Scaling 2 for species and site scores
## * Species are scaled proportional to eigenvalues
## * Sites are unscaled: weighted dispersion equal on all dimensions
## * General scaling constant of scores: 4.93332
##
##
## Species scores
##
## RDA1 PC1 PC2 PC3 PC4 PC5
## RI 6.164e-05 0.006766 -0.0027906 0.001443 0.001003 -0.0006039
## Na -2.177e-01 -0.423708 -1.1896878 -0.802298 -0.127952 -0.0081867
## Mg -7.082e-01 -1.943017 -0.5819804 0.515740 0.600069 0.0399950
## Al 3.060e-01 -0.296512 0.2471444 0.226655 -0.564066 0.2380706
## Si 2.683e-02 -0.715098 1.3444594 -0.549095 0.330432 -0.0552179
## K 1.054e-01 -0.289194 0.2676415 0.153595 -0.215380 0.1439493
## Ca 3.605e-01 3.501644 -0.1493831 0.091594 0.335991 0.0649667
## Ba 4.946e-02 0.183784 -0.0005734 0.318738 -0.313081 -0.4360001
## Fe 2.934e-02 0.034801 0.0124987 0.051718 -0.014555 -0.0109148
##
##
## Site scores (weighted sums of species scores)
##
## RDA1 PC1 PC2 PC3 PC4 PC5
## 1 -1.4339 -0.08483 -0.58103 0.3921 0.34455 0.03627
## 2 -0.9342 -0.23104 -0.09355 -0.4244 -0.40769 -0.06320
## 3 -0.7459 -0.23923 0.13105 -0.3224 -0.40484 -0.01532
## 4 -0.6680 -0.13896 0.05276 0.0700 -0.16978 0.07211
## 5 -0.6964 -0.18207 0.21579 -0.1948 -0.08712 -0.12232
## 6 -0.3891 -0.17193 0.36383 0.2010 -0.29294 0.27612
## ....
##
##
## Site constraints (linear combinations of constraining variables)
##
## RDA1 PC1 PC2 PC3 PC4 PC5
## 1 -0.3612 -0.08483 -0.58103 0.3921 0.34455 0.03627
## 2 -0.3612 -0.23104 -0.09355 -0.4244 -0.40769 -0.06320
## 3 -0.3612 -0.23923 0.13105 -0.3224 -0.40484 -0.01532
## 4 -0.3612 -0.13896 0.05276 0.0700 -0.16978 0.07211
## 5 -0.3612 -0.18207 0.21579 -0.1948 -0.08712 -0.12232
## 6 -0.3612 -0.17193 0.36383 0.2010 -0.29294 0.27612
## ....
##
##
## Biplot scores for constraining variables
##
## RDA1 PC1 PC2 PC3 PC4 PC5
## FAC2 1 0 0 0 0 0
##
##
## Centroids for factor constraints
##
## RDA1 PC1 PC2 PC3 PC4 PC5
## FAC1 -0.3612 0 0 0 0 0
## FAC2 0.4134 0 0 0 0 0После включения в анализ объясняющего фактора “Тип производства стекла” появляется связанная с ним ось новой переменной RDA1, а к матрице нагрузок на главные компоненты добавляется столбец соответствующих канонических коэффициентов. Собственное значение, определяющее RDA1, невелико и составляет только 3.2% от общей вариации данных.
Сформируем ординационную диаграмму в координатах {RDA1, PC1}, на которой обозначим координаты центроидов и выделим 95% доверительные области в виде эллисов (рис. 2.11):
library(ggplot2)
rda.scores <- as.data.frame(vegan::scores(mod.rda,
display = "sites", scales = 3))
rda.scores <- cbind(FAC, rda.scores)
centroids <- aggregate(cbind(RDA1, PC1) ~ FAC, rda.scores, mean)
# функция для std.err
f <- function(z)sd(z)/sqrt(length(z))
se <- aggregate(cbind(RDA1, PC1) ~ FAC, rda.scores, f)
names(se) <- c("FAC", "RDA1.se", "PC1.se")
# объединяем координаты центроидов и стандартные ошибки
centroids <- merge(centroids, se, by = "FAC")
# формируем диаграмму
ggplot() + geom_point(data = rda.scores,
aes(x = RDA1, y = PC1, shape = FAC, colour = FAC), size = 2) +
xlim(c(-2, 5)) + ylim(c(-0.75, 1)) +
scale_colour_manual(values = c('purple', 'blue')) +
stat_ellipse(data = rda.scores, aes(x = RDA1, y = PC1, fill = FAC),
geom = "polygon", level = 0.8, alpha = 0.2) +
geom_point(data = centroids, aes(x = RDA1, y = PC1, colour = FAC),
shape = 1, size = 4) + theme_bw()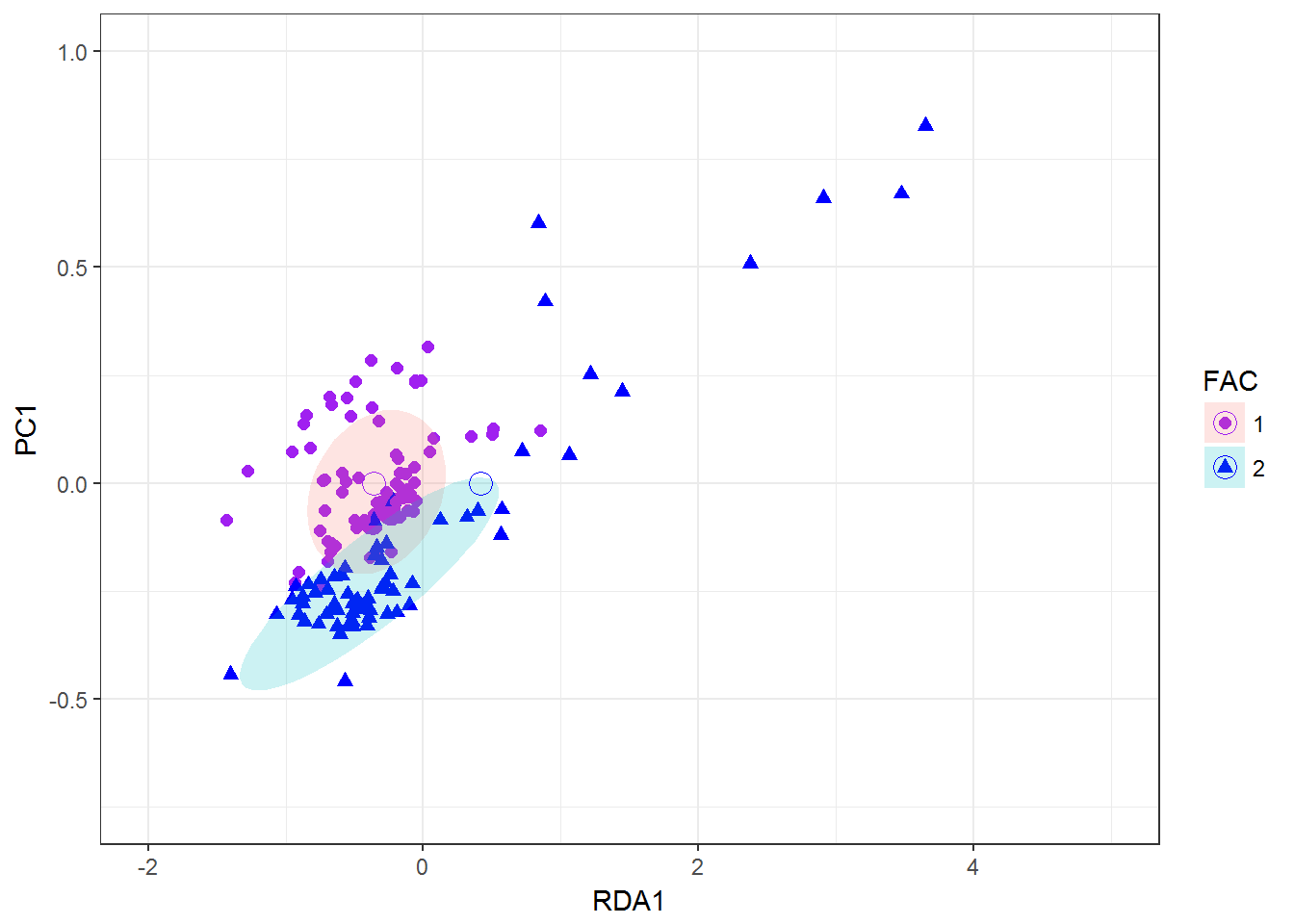
Рисунок 2.11: Ординационная диаграмма, построенная методом RDA (не показаны 7 точек за пределами верхнего правого угла графика)
Несмотря на небольшую долю дисперсии, объясняемой фактором способа производства стекла F, координаты центроидов, определяющих центры тяжести сравниваемых групп, стали располагаться на некотором расстоянии друг от друга на рис. 2.11, что позволяет мысленно провести разделяющую линию между ними.
В арсенал многомерных процедур входят не только задачи снижения размерности или распознавания групп, но и методы, предназначенные для традиционной проверки статистических гипотез. Многомерный дисперсионный анализ является обобщением обычного одномерного дисперсионного анализа и предназначен для выявления различий между группами по совокупности средних значений комплекса признаков. Нулевая гипотеза заключается в предположении о равенстве векторов средних значений для сравниваемых групп наблюдений.
Для формирования модели многомерного дисперсионного анализа можно воспользоваться функциями aov(), lm() либо manova(), которые приводят к идентичным результатам. Получить традиционную дисперсионную таблицу можно с использованием функции anova():
mod.an <- manova(as.matrix(Y) ~ FAC)
anova(mod.an)## Analysis of Variance Table
##
## Df Pillai approx F num Df den Df Pr(>F)
## (Intercept) 1 1.00000 65548701 9 153 < 2.2e-16 ***
## FAC 1 0.27971 7 9 153 6.106e-08 ***
## Residuals 161
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Теснота связи между химическим составом стекла Y и способом его изготовления FAC была оценена с использованием статистики Пиллая (Pillai’s trace).
Поскольку мы имеем лишь две группы наблюдений, то статистическая проверка гипотезы о равенстве средних двух векторов \(H_0: \bar{X}_1 = \bar{X}_2\) может быть осуществлена также с использованием статистики Хотеллинга, которая является многомерным аналогом t-критерия Стьюдента:
library(Hotelling)
split.data <- split(Y, FAC)
(summ.hot <- hotelling.test(split.data[[1]], split.data[[2]],
perm = TRUE, B = 1000, progBar = FALSE))## Test stat: 6.6015
## Numerator df: 9
## Denominator df: 153
## Permutation P-value: 0
## Number of permutations : 1000В выполненном перестановочном тесте ни одна из 1000 статистик Хотеллинга, полученных при случайном перемешивании данных, не превысила тестируемое значение, что свидетельствует о высокой статистической значимости разделяющего фактора.