7.4 Нелинейные классификаторы в R
Квадратичный дискриминантный анализ (QDA) является нелинейным обобщением метода LDA, который не использует предположения об однородности ковариационной матрицы. В качестве решающего правила применяется квадратичная функция
\[d_k = -0.5(\mathbf{x} - \boldsymbol{\mu}_k)^T \mathbf{C}_k^{-1} (\mathbf{x} - \boldsymbol{\mu}_k) - 0.5 \ln |\mathbf{C}_k| + \ln \pi_k,\]
где \(|\mathbf{C}_k|\) - детерминант ковариационной матрицы \(k\)-го класса, \(\mathbf{C}_k^{-1}\) - ее обратная матрица; \(\pi_k\) априорная вероятность наблюдения объектов \(k\)-го класса. Экзаменуемый объект так же относится к классу с максимальным значением \(d_k\).
Квадратичный дискриминантный анализ весьма эффективен, когда разделяющая поверхность между классами имеет ярко выраженный нелинейный характер (например, параболоид или эллипсоид в 3D-случае). Однако он сохраняет большинство недостатков LDA: использует предположение о нормальности распределения и не работает, когда матрицы ковариаций вырождены (например, при большом числе переменных). Другим недостатком QDA является то, что уравнение разделяющей гиперповерхности выражено в неявном виде и не может быть использовано для “объяснения” результатов.
Для проведения квадратичного дискриминантного анализа можно воспользоваться функцией qda() из пакета MASS:
require(MASS)
QDA.iris <- qda(Species ~ Petal.Length + Petal.Width, data = iris)
pred <- predict(QDA.iris)$class
(table(Факт = iris$Species, Прогноз = pred))## Прогноз
## Факт setosa versicolor virginica
## setosa 50 0 0
## versicolor 0 49 1
## virginica 0 2 48Acc <- mean(pred == iris$Species)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=98%"Чтобы показать на рис. 7.8 форму разделяющих поверхностей для классов цветков ириса используем только две наиболее значимые переменные, определяющие размеры лепестка:
library(klaR)
partimat(Species ~ Petal.Length + Petal.Width, data = iris, method = "qda")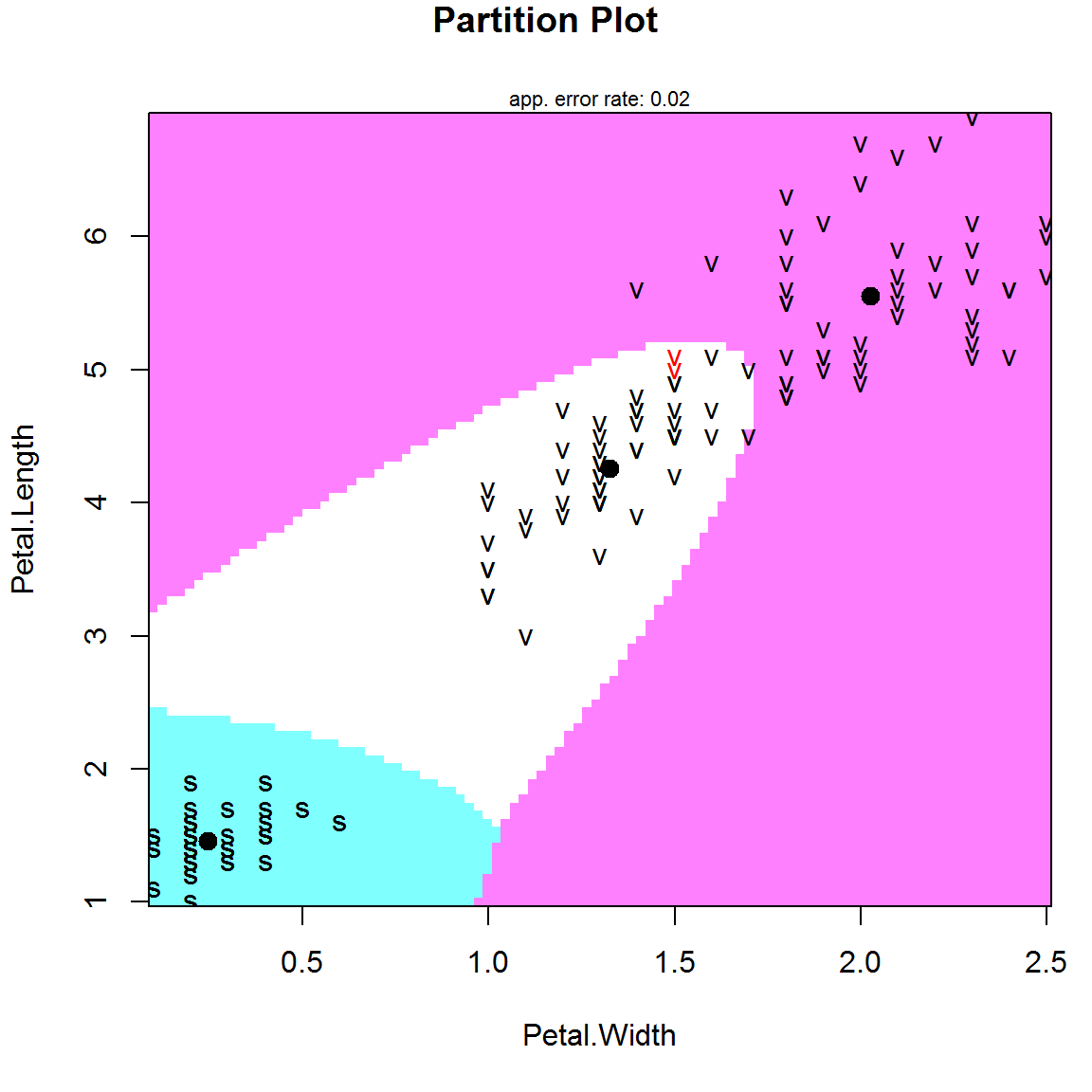
Рисунок 7.8: Разделяющие границы, полученные в результате применения квадратичного дискриминантого анализа для классификации цветков ириса (ошибочное распознавание выделено шрифтом красного цвета); жирными точками показаны центроиды классов
C использованием функции train() из пакета caret сравним точность классификации по полной модели и модели с двумя предикторами на основании 10-кратной перекрестной проверки:
library(caret)
set.seed(123)
# Используем только размеры лепестка
train(Species ~ Petal.Length + Petal.Width,
data = iris, method = "qda",
trControl = trainControl(method = "cv"))## Quadratic Discriminant Analysis
##
## 150 samples
## 2 predictor
## 3 classes: 'setosa', 'versicolor', 'virginica'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 135, 135, 135, 135, 135, 135, ...
## Resampling results:
##
## Accuracy Kappa
## 0.9733333 0.96
##
## # Используем весь набор признаков
train(Species ~ ., data = iris, method = "qda",
trControl = trainControl(method = "cv"))## Quadratic Discriminant Analysis
##
## 150 samples
## 4 predictor
## 3 classes: 'setosa', 'versicolor', 'virginica'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 135, 135, 135, 135, 135, 135, ...
## Resampling results:
##
## Accuracy Kappa
## 0.9733333 0.96
##
## Очевидно, что ботаникам вполне можно было обойтись без утомительной работы по фиксации размеров чашелистника.
Регуляризованный дискриминантный анализ (Regularized Discriminant Analysis, RDA), предложенный Дж. Фридманом, является своеобразным промежуточным звеном между LDA и QDA. Пусть \(\lambda\) - положительный параметр, подобранный таким образом, чтобы управлять степенью кривизны разделяющей поверхности. При его использовании регуляризованная ковариационная матрица \(\mathbf{C}_k (\lambda)\) оказывается как бы более “притянутой” к общей ковариационной матрице \(\mathbf{C}_0\), чем индивидуальная \(\mathbf{C}_k\) для \(k\)-го класса:
\[\mathbf{C}_k(\lambda) = (1-\lambda) \mathbf{C}_k + \lambda \mathbf{C}_0.\]
Новая ковариационная матрица всегда обратима и может быть использована в вычислениях. При этом гарантируется, что полученная разделяющая поверхность имеет большую выпуклость, чем при LDA, но меньшую, чем при QDA, к которой она сходится при \(\lambda = 0\).
Более точная регуляризация получается при искусственном увеличении числа доступных объектов обучения за счет добавления к данным шума, интенсивность которого связана со вторым параметром - \(\gamma\):
\[ \mathbf{C}_k(\lambda, \gamma) = (1-\gamma) \mathbf{C}_k(\lambda) + \gamma \text{ trace}[\mathbf{C}_k(\lambda)] \mathbf{I} / m,\]
где \(\text{ trace}[\mathbf{C}_k(\lambda)]\) - диагональные элементы матрицы \(\mathbf{C}_k(\lambda)\), или вектор дисперсий исходных m переменных, описывающих объекты \(k\)-го класса; \(\mathbf{I}\) - единичная матрица.
При экстремальных значениях \(\lambda\) и \(\gamma\) ковариационная структура сводится к четырем особым случаям:
- \((\gamma = 0, \lambda = 0)\): QDA - индивидуальная ковариация в каждой группе;
- \((\gamma = 0, \lambda = 1)\): LDA - общая матрица ковариации;
- \((\gamma = 1, \lambda = 0)\): исходные переменные условно независимы (подобно тому, что предполагает наивный байесовский классификатор), но их внутригрупповые дисперсии однородны;
- \((\gamma = 1, \lambda = 1)\): дисперсии равны для всех групп и классификация объектов осуществляется по евклидовым расстояниям до центроидов.
Подбор оптимальных значений \((\lambda, \gamma)\) можно осуществить с помощью функции train() из пакета caret, задав, например, 10-кратную перекрестную проверку:
library(klaR)
set.seed(123)
# 1 - этап грубой оптимизации
train(Species ~ ., data = iris, method = "rda",
trControl = trainControl(method = "cv"))## Regularized Discriminant Analysis
##
## 150 samples
## 4 predictor
## 3 classes: 'setosa', 'versicolor', 'virginica'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 135, 135, 135, 135, 135, 135, ...
## Resampling results across tuning parameters:
##
## gamma lambda Accuracy Kappa
## 0.0 0.0 0.9733333 0.96
## 0.0 0.5 0.9800000 0.97
## 0.0 1.0 0.9800000 0.97
## 0.5 0.0 0.9666667 0.95
## 0.5 0.5 0.9666667 0.95
## 0.5 1.0 0.9600000 0.94
## 1.0 0.0 0.9133333 0.87
## 1.0 0.5 0.9200000 0.88
## 1.0 1.0 0.9200000 0.88
##
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were gamma = 0 and lambda = 1.# 2 - этап с диапазоном lambda = 0.1:0.5 и gamma = 0.02:0.1
RDAGrid <- expand.grid(.lambda = (1:5)/10, .gamma = (1:5)/50)
set.seed(123)
RDA.iris <- train(Species ~ ., data = iris, method = "rda",
tuneGrid = RDAGrid, trControl = trainControl(method = "cv"))# Оценка точности итоговой модели:
pred <- predict(RDA.iris)
Acc <- mean(pred == iris$Species)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=98%"Обратим внимание, что при выполнении скрипта нужно отключить загруженный пакет vegan, где также есть функция rda().
Машина опорных векторов SVM, описанная в разделах 6.2-6.3, является бинарным классификатором и естественным образом на случай с несколькими классами не переносится. Однако имеется возможность использовать этот метод, применяя стратегии “каждый против каждого” (one against one) или “один против всех” (one against all). Применим метод опорных векторов к данным по ирисам для нахождения разделяющих поверхностей, которые по умолчанию в функции svm() формируются с использованием радиального ядра RBF:
library(e1071)
SVM.iris <- svm(Species ~ ., data = iris)
pred.DV <- predict(SVM.iris, iris[, 1:4], decision.values = TRUE)
ind <- sort(sample(150, 9))
data.frame(attr(pred.DV, "decision.values")[ind, ], iris$Species[ind])## setosa.versicolor setosa.virginica versicolor.virginica
## 8 1.1937271 1.0845292 0.7297775
## 36 1.1850954 1.0742373 0.7599030
## 47 1.1307464 1.0913100 0.4741185
## 50 1.1921235 1.0803233 0.7669207
## 68 -1.1578968 -0.5659738 1.9180355
## 69 -0.9996815 -0.9207963 0.5281939
## 94 -1.0699699 -0.2130134 1.2447205
## 126 -0.7653335 -1.1259098 -0.9860806
## 150 -1.1809167 -1.0602949 -0.4349388
## iris.Species.ind.
## 8 setosa
## 36 setosa
## 47 setosa
## 50 setosa
## 68 versicolor
## 69 versicolor
## 94 versicolor
## 126 virginica
## 150 virginicaБыли получены пороговые значения (decision values) при распознавании “класс1”/“класс2”: если пороговое значение положительно, то побеждает “класс 1”, иначе - “класс 2”. Окончательный результат определяется голосованием, т.е. в данном случае достаточно победить обоих оппонентов.
pred <- predict(SVM.iris, iris[, 1:4], type = "response")
(table(Факт = iris$Species, Прогноз = pred))## Прогноз
## Факт setosa versicolor virginica
## setosa 50 0 0
## versicolor 0 48 2
## virginica 0 2 48Acc = mean(pred == iris$Species)
paste("Точность=", round(100*Acc, 2), "%", sep = "")## [1] "Точность=97.33%"Вид ядерных функций многоклассовой SVM не может быть непосредственно визуализирован, поэтому для обозначения решающих границ применим косвенный метод метрического многомерного шкалирования MDS (multidimensional scaling; рис. 7.9).
plot(cmdscale(dist(iris[,-5])), col = as.integer(iris[, 5]) + 1,
pch = c("o","+")[1:150 %in% SVM.iris$index + 1], font = 2,
xlab = "Шкала 1", ylab = "Шкала 2" )
legend(0,1.2, c("setosa", "versicolor", "virginica"),
pch = "o", col = 2:4)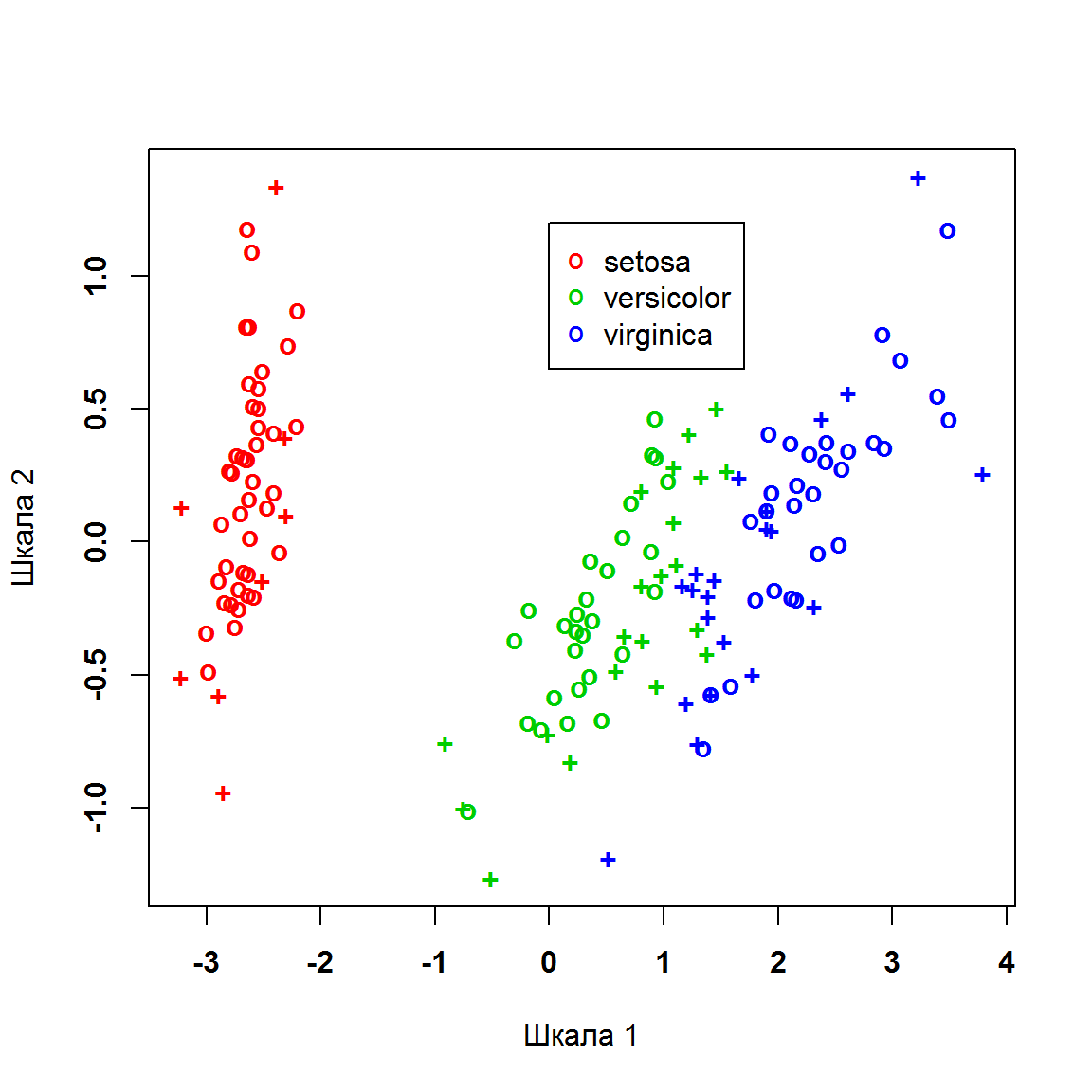
Рисунок 7.9: Ординационная диаграмма наблюдений из набора данных по ирисам, построенная методом многомерного шкалирования (крестиками соответствующего цвета показаны опорные векторы)
Здесь функция dist() строит матрицу евклидовых расстояний размерностью \(150 \times 150\) для всех пар наблюдений по всей совокупности измеренных показателей. Функция cmdscale() проецирует эту матрицу на плоскость таким образом, чтобы минимизировать искажения взаимных дистанций между объектами при сокращении исходного многомерного пространства до двумерной ординации (рис. 7.9). Опорные векторы, представленные на диаграмме крестиками, задают границы разделяющих RBF-поверхностей, аккуратно окаймляющих области каждого класса.