ГЛАВА 4 Построение регрессионных моделей различного типа

4.1 Селекция оптимального набора предикторов линейной модели

Модель множественной линейной регрессии является, безусловно, весьма полезной и широко применяемой для прогнозирования количественного отклика. Считается, что наиболее эффективный путь улучшения качества регрессии - исключение незначимых коэффициентов, или, выражаясь точнее, отбор информативного комплекса \(S_q\) из \(q\) переменных \((q < m)\). Причины, по которым стоит проводить селекцию “оптимального подмножества” предикторов, Дж. Фаравэй (Faraway, 2006) видит в следующем:

  1. Принцип бритвы Оккама утверждает, что из нескольких вероятных объяснений явления лучшим является самое простое. Компактная модель, из которой удалены избыточные предикторы, лучше объясняет имеющиеся данные.
  2. Ненужные предикторы добавляют шум к оценке влияния других интересующих нас факторов. Иначе степени свободы (часто ограниченные) будут тратиться впустую.
  3. При наличии коллинеарности некоторые переменные будут “пытаться сделать одну и ту же работу” (т.е., повторно объяснять вариацию значений зависимой переменной).
  4. Если модель используется для прогнозирования, то можно сэкономить время и/или деньги, не измеряя избыточные переменные.

Алгоритмы выбора оптимального подмножества \(S_q\) обычно основаны на последовательном “переборном” процессе, при котором многократно создаются модели с различными наборами предикторов, лучшая из которых определяется по некоторому критерию эффективности (ошибка или точность модели, \(R^2\), АIC и проч.). Рассмотрим технику применения и оценим полученные результаты с использованием трех таких методов: пошаговый (forward/backward) метод селекции, рекурсивное исключение и генетический алгоритм, представленные в пакете caret.

В качестве примера рассмотрим построение регрессионных моделей, прогнозирующих обилие водорослей группы a1 в зависимости от гидрохимических показателей воды и условий отбора проб в различных водотоках (см. подробное описание таблицы переменных в разделе 3.4):

library(DMwR)
data(algae)
library(caret)

# Заполним пропуски в данных на основе алгоритма бэггинга
pPbI <- preProcess(algae[, 4:11], method = 'bagImpute')
algae[, 4:11] <- predict(pPbI, algae[, 4:11])

# Сохраним таблицу для использования в дальнейшем
# save(algae, file="algae.RData")

Важные предварительные выводы можно сделать, сформировав корреляционную матрицу предикторов (рис. 4.1):

Mcor <- cor(algae[, 4:11])
library(corrplot)
corrplot(Mcor, method = "color", addCoef.col = " darkgreen", 
         addgrid.col = "gray33", tl.col = "black")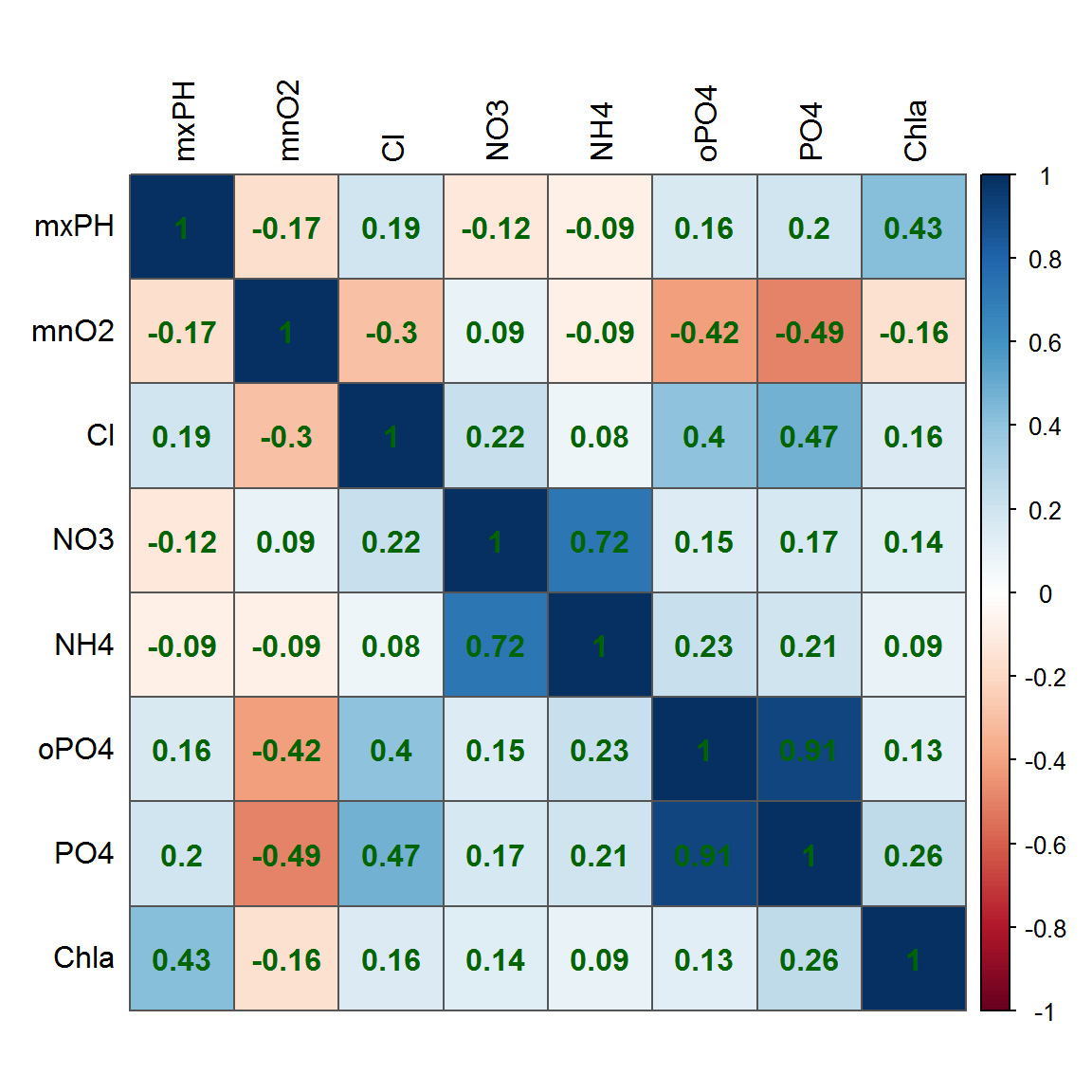
Корреляционная матрица показателей качества воды в реках

Рисунок 4.1: Корреляционная матрица показателей качества воды в реках

Очевидно, что между предикторами существуют корреляционные связи умеренной силы, а коллинеарность, в целом, выражена слабо.

4.1.1 Полная регрессионная модель и пошаговая процедура

Построим сначала линейную модель на основе полного набора переменных:

lm.a1 <- lm(a1 ~ ., data = algae[, 1:12])
summary(lm.a1)
## 
## Call:
## lm(formula = a1 ~ ., data = algae[, 1:12])
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.286 -11.941  -2.666   7.199  62.938 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)   
## (Intercept)  40.660398  23.935937   1.699  0.09106 . 
## seasonspring  3.595224   4.137801   0.869  0.38605   
## seasonsummer  0.302678   3.994759   0.076  0.93969   
## seasonwinter  3.472394   3.849457   0.902  0.36821   
## sizemedium    3.609751   3.741636   0.965  0.33594   
## sizesmall     9.910150   4.128996   2.400  0.01739 * 
## speedlow      3.342744   4.685579   0.713  0.47650   
## speedmedium  -0.253552   3.213791  -0.079  0.93720   
## mxPH         -3.305772   2.690630  -1.229  0.22078   
## mnO2          1.047343   0.703971   1.488  0.13852   
## Cl           -0.037342   0.033711  -1.108  0.26944   
## NO3          -1.524650   0.549128  -2.776  0.00606 **
## NH4           0.001636   0.001002   1.633  0.10416   
## oPO4         -0.001989   0.039522  -0.050  0.95993   
## PO4          -0.054853   0.030371  -1.806  0.07253 . 
## Chla         -0.068090   0.078898  -0.863  0.38926   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 17.64 on 184 degrees of freedom
## Multiple R-squared:  0.3686, Adjusted R-squared:  0.3171 
## F-statistic:  7.16 on 15 and 184 DF,  p-value: 2.965e-12

Отметим, что при всей внушительной адекватности модели в целом (по \(F\)-критерию), почти все коэффициенты оцениваются как статистически незначимые. Выполним стандартную пошаговую процедуру включений с исключениями “слабых” предикторов, используя функцию step():

lm_step.a1 <- step(lm.a1, trace = 0)
summary(lm_step.a1)
## 
## Call:
## lm(formula = a1 ~ size + mxPH + mnO2 + NO3 + NH4 + PO4, data = algae[, 
##     1:12])
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.892 -11.716  -3.773   7.617  64.945 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 47.4021122 21.3532410   2.220 0.027596 *  
## sizemedium   3.3970379  3.3654060   1.009 0.314054    
## sizesmall   10.4380289  3.7845961   2.758 0.006377 ** 
## mxPH        -3.7892907  2.4251489  -1.562 0.119817    
## mnO2         0.8785464  0.6289587   1.397 0.164078    
## NO3         -1.7435933  0.5143279  -3.390 0.000848 ***
## NH4          0.0017711  0.0009525   1.859 0.064493 .  
## PO4         -0.0613682  0.0116599  -5.263 3.77e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 17.45 on 192 degrees of freedom
## Multiple R-squared:  0.3557, Adjusted R-squared:  0.3322 
## F-statistic: 15.14 on 7 and 192 DF,  p-value: 1.064e-15

Доля значимых предикторов стала существенно выше. Проверим также, можно ли считать статистически значимой некоторое увеличение ошибки модели:

anova(lm.a1, lm_step.a1)
## Analysis of Variance Table
## 
## Model 1: a1 ~ season + size + speed + mxPH + mnO2 + Cl + NO3 + NH4 + oPO4 + 
##     PO4 + Chla
## Model 2: a1 ~ size + mxPH + mnO2 + NO3 + NH4 + PO4
##   Res.Df   RSS Df Sum of Sq      F Pr(>F)
## 1    184 57269                           
## 2    192 58438 -8   -1169.7 0.4698 0.8764

Выполним тестирование обоих моделей функцией train() из пакета caret (см. раздел 3.5) с использованием 10-кратной перекрестной проверки:

lm.a1.cv <- train(a1 ~ ., data = algae[, 1:12], method = 'lm',
                  trControl = trainControl(method = "cv"))

lm_step.a1.cv <- train(a1 ~ size + mxPH + mnO2 + NO3 + NH4 + PO4, 
                       data = algae[, 1:12], method = 'lm',
                       trControl = trainControl(method = "cv"))

Преимущества модели, полученной с использованием пошаговой процедуры отбора предикторов, вполне очевидны.

4.1.2 Рекурсивное исключение переменных

Алгоритм рекурсивного исключения (RFE - Recursive Feature Elimination) выполняется следующим образом. Вначале строится модель по всем предикторам, которые ранжируются по их важности. Далее рассматривается последовательность подмножеств \(\mathbf{S}\) (\(\mathbf{S_1} > \mathbf{S_2}\), и т.д.) из переменных наивысшего ранга. На каждой итерации подмножества Si ранги предикторов пересматриваются, а модели пересчитываются. Итоговая модель основывается на подмножестве \(\mathbf{S_i}\), обеспечивающем оптимум заданному критерию качества.

Функция rfe() из пакета caret включает алгоритм RFE в процедуру ресэмплинга, и тогда цикл рекурсивного исключения приобретает следующий вид:

Синтаксис параметров функций rfe() и rfeControl() в целом похож на таковой у функций train() и trainControl() (см. раздел 3.5). Отметим, что функция rfe() не осуществляет оптимизацию модели, включающей номинальные предикторы, поэтому их необходимо преобразовать в индикаторные переменные с использованием функции model.matrix(). После этого в новой таблице х вместо каждого из факторов образуется несколько бинарных (0/1) столбцов с наименованиями, соответствующими уровням этого фактора (рис. 4.2):4

x <- model.matrix(a1 ~ ., data = algae[, 1:12])[, -1]
set.seed(10)
ctrl <- rfeControl(functions = lmFuncs, method = "cv",
                   verbose = FALSE, returnResamp = "final")
lmProfileF <- rfe(as.data.frame(x), algae$a1, 
                  sizes = 1:10, rfeControl = ctrl)

predictors(lmProfileF)
## [1] "NO3"          "sizesmall"    "PO4"          "NH4"         
## [5] "mnO2"         "mxPH"         "Cl"           "seasonwinter"
summary(lmProfileF$fit)
## 
## Call:
## lm(formula = y ~ ., data = tmp)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -36.254 -12.037  -3.009   7.770  64.905 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  54.544067  20.665487   2.639  0.00899 ** 
## NO3          -1.530537   0.531707  -2.879  0.00445 ** 
## sizesmall     7.455181   3.024325   2.465  0.01458 *  
## PO4          -0.055530   0.012328  -4.504 1.16e-05 ***
## NH4           0.001498   0.000974   1.538  0.12565    
## mnO2          0.803687   0.637043   1.262  0.20864    
## mxPH         -4.341665   2.411078  -1.801  0.07333 .  
## Cl           -0.036081   0.032476  -1.111  0.26796    
## seasonwinter  2.009832   2.714520   0.740  0.45997    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 17.45 on 191 degrees of freedom
## Multiple R-squared:  0.3584, Adjusted R-squared:  0.3315 
## F-statistic: 13.34 on 8 and 191 DF,  p-value: 2.944e-15
require(gridExtra)
grid.arrange(ggplot(lmProfileF, metric = "RMSE"),
             ggplot(lmProfileF, metric = "Rsquared"), ncol = 2)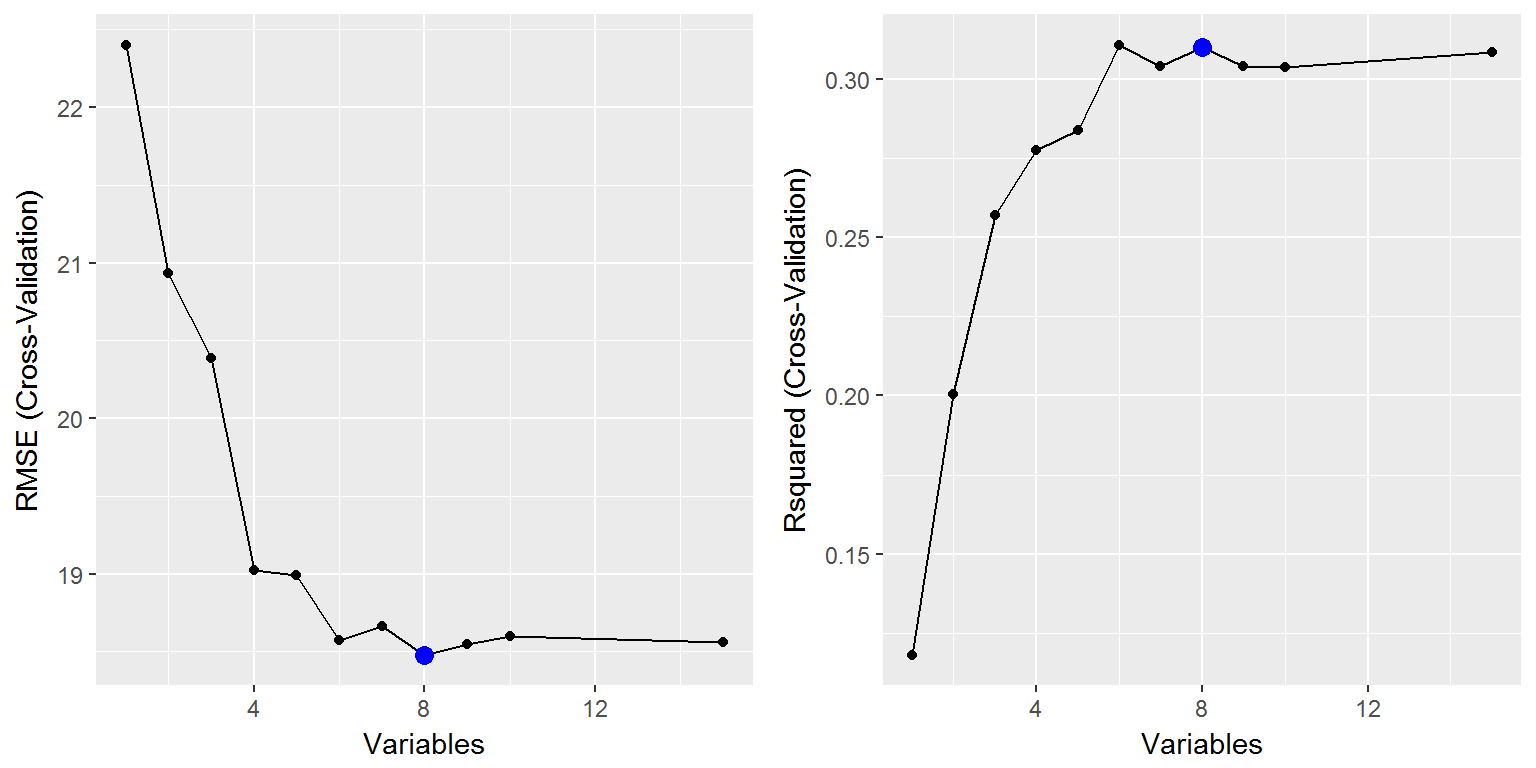
Изменение корня из среднеквадратичной ошибки и коэффициента детерминации в зависимости от числа предикторов (по результатам перекрестной проверки)

Рисунок 4.2: Изменение корня из среднеквадратичной ошибки и коэффициента детерминации в зависимости от числа предикторов (по результатам перекрестной проверки)

Нельзя утверждать, что нам удалось достигнуть серьезных успехов, применив метод RFE: пошаговая модель lm_step.a1 была компактнее и чуть лучше (по результатам перекрестной проверки), хотя и уступала модели RFE по величине ошибки на обучающей выборке.

4.1.3 Генетический алгоритм

Генетический алгоритм, позаимствованный у природных аналогов и разработанный Дж. Холландом (Holland, 1975), отличается от большинства иных процедур селекции тем, что поиск оптимального решения развивается не сам по себе, а с учетом предыдущего опыта. Смысл его заключается в следующем:

  • формируемое решение кодируется как вектор \(x^0\), который называется хромосомой и соответствует битовой маске, т.е. двоичному представлению набора исходных переменных;
  • инициализируется исходная “популяция” \(\Pi^0 (x_1^0, \dots, x_{\lambda})\) потенциальных решений, состоящая из некоторого количества хромосом \(\lambda\);
  • каждой хромосоме в популяции присваиваются две оценки: значение эффективности \(\mu(x_i^0)\) в соответствии с заданной функцией оптимальности и вероятность воспроизведения \(P(x_i^0)\), которая зависит от “перспективности” этой хромосомы;
  • в соответствии с вероятностями воспроизведения хромосомы производят потомков, используя операции кроссинговера (обмена фрагментами между хромосомами) и мутации (замена значения бита 0/1 на противоположный) - см. рис. 4.3;
  • в ходе репродуцирования создается новая популяция хромосом, причем с большей вероятностью воспроизводятся наиболее перспективные фрагменты “генетического кода”;
  • формирование новой популяции многократно повторяется и осуществляется поиск субоптимальных моделей;
  • процесс останавливается, если получено удовлетворительное решение, либо исчерпано все отведенное на эволюцию время.
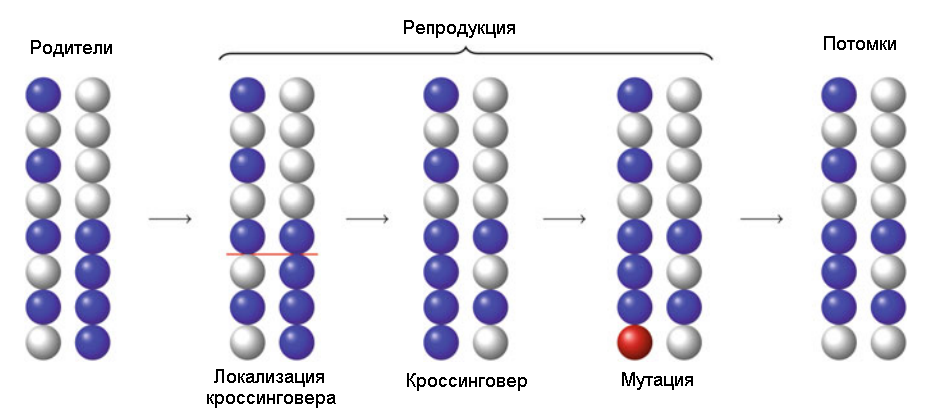
Схема кроссинговера и мутации во время применения генетического алгоритма

Рисунок 4.3: Схема кроссинговера и мутации во время применения генетического алгоритма

Синтаксис пары функций gafs() и gafsControl(), реализующих генетический алгоритм в пакете caret, в целом аналогичен таковому у функций rfe() и rfeControl(), но требует задания дополнительных аргументов, регулирующих скорость эволюции. Похоже, что здесь преобразовывать факторы в индикаторные переменные не требуется (эта проблема нами не исследовалась):

# Выполнение этого кода потребует более 30 мин.
# Результаты вычислений здесь не приводятся
set.seed(10)
ctrl <- gafsControl(functions = rfGA, method = "cv", 
                    verbose = FALSE, returnResamp = "final")
lmProfGafs <- gafs(algae[, 1:11], algae$a1, 
                   iters = 10, # 10 генераций
                   gafsControl = ctrl)
lmProfGafs
lm_gafs.a1 <- lm(a1 ~ size + mxPH + Cl + NO3 + PO4,
                 data = algae[, 1:12])
train(a1 ~ size + mxPH + Cl + NO3 + PO4,
      data = algae[, 1:12], method = 'lm',
      trControl = trainControl(method = "cv"))
## Linear Regression 
## 
## 200 samples
##   5 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 180, 179, 180, 180, 180, 180, ... 
## Resampling results:
## 
##   RMSE      Rsquared 
##   17.71498  0.3419793
## 
## Tuning parameter 'intercept' was held constant at a value of TRUE
##

Несмотря на большие затраты вычислительных ресурсов (поиск решения продолжался более 30 мин.), была получена комбинация предикторов, превосходящая по критериям RMSE и Rsquared все три предыдущие модели.

4.1.4 Тестирование моделей с использованием дополнительного набора данных

Возникает естественный вопрос: а какой из четырех полученных моделей следует все же отдать предпочтение при прогнозировании? Хорошую возможность ответить на него предоставляет нам Л. Торго (Torgo, 2011), подготовивший на сайте своей книги (http://www.dcc.fc.up.pt) специально предназначенный для этого набор данных из 140 наблюдений (см. файл Eval.txt с предикторами и Sols.txt со значениями отклика). Пропущенные значения заполним с использованием алгоритма бэггинга:

Eval <- read.table('Eval.txt', header = FALSE, dec = '.',
                   col.names = c('season', 'size', 'speed', 'mxPH', 'mnO2', 'Cl',
                                 'NO3','NH4','oPO4','PO4','Chla'),
                   na.strings = c('XXXXXXX'))
Sols <- read.table('Sols.txt', header = FALSE, dec = '.',          
                   col.names = c('a1', 'a2', 'a3', 'a4', 'a5', 'a6', 'a7'),
                   na.strings = c('XXXXXXX'))
ImpEval <- preProcess(Eval[, 4:11], method = 'bagImpute')
Eval[, 4:11] <- predict(ImpEval, Eval[, 4:11])
# Cохраним данные для дальнейшего использования
save(Eval, Sols, file = "algae_test.RData")
y <- Sols$a1
EvalF <- as.data.frame(model.matrix(y ~ ., Eval)[, -1])

Выполним прогноз для набора предикторов тестовой выборки и оценим точность каждой модели по трем показателям: среднему абсолютному отклонению (MAE), корню из среднеквадратичного отклонения (RSME) и квадрату коэффициента детерминации Rsq = 1 - NSME, где NSME - относительная ошибка, равная отношению средних квадратов отклонений от регрессии и от общего среднего:

# Функция, выводящая вектор критериев
ModCrit <- function(pred, fact) {
    mae <- mean(abs(pred - fact))
    rmse <- sqrt(mean((pred - fact)^2))
    Rsq <- 1 - sum((fact - pred)^2)/sum((mean(fact) - fact)^2)
    c(MAE = mae, RSME = rmse,  Rsq = Rsq )
}
y <- Sols$a1
EvalF <- as.data.frame(model.matrix(y ~ ., Eval)[, -1])
Result <- rbind(
    lm_full = ModCrit(predict(lm.a1,Eval), Sols[, 1]),
    lm_step = ModCrit(predict(lm_step.a1, Eval), Sols[, 1]),
    lm_rfe = ModCrit(predict(lmProfileF$fit, EvalF), Sols[, 1]),
    lm_gafs = ModCrit(predict(lm_gafs.a1, Eval), Sols[, 1]))
Result
##              MAE     RSME       Rsq
## lm_full 12.65429 16.82707 0.3253951
## lm_step 12.47924 16.63718 0.3405343
## lm_rfe  12.33770 16.51345 0.3503067
## lm_gafs 12.72925 17.19677 0.2954261

Вероятно, нет смысла делать серьезные выводы из того, что рейтинг лучших моделей при перекрестной проверке и при независимом тестировании на объектах, не участвовавших в построении моделей, оказался столь несовпадающим. Во-первых, разброс критериев точности моделей находится в пределах доверительных интервалов, поэтому их ранжирование, строго говоря, можно трактовать как обусловленное случайными причинами. Во-вторых, многое зависит от того, например, насколько неоднородны были между собой обе выборки. И, наконец, напомним, что одним из основных принципов моделирования сложных систем является принцип множественности моделей, сформулированный В. В. Налимовым и заключающийся в возможности представления одной и той же системы множеством различных моделей в зависимости от целей исследования.

  1. Полученные вами результаты могут отличаться от приведенных в силу случайного характера подвыборок, формируемых в ходе перекрестной проверки.↩