11.4 Дескриптивные модели (обучение без учителя)
11.4.1 Кластерный анализ
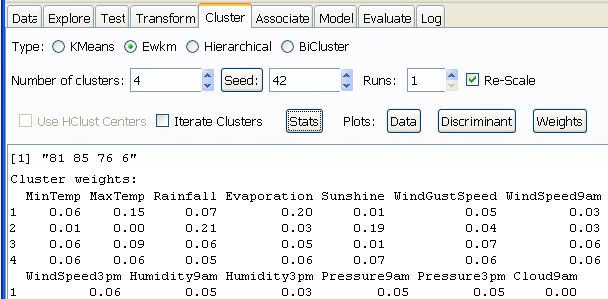
Методы кластерного анализа подробно рассматривались в главе 10, и мы уже не рассчитывали обнаружить в среде rattle какие-то новые сюжеты. Однако, приступив к кластеризации признаков привычного набора наблюдений за погодой в г. Канберра, мы увидели еще не представленный читателям алгоритм EWKM (Entropy Weighted K-Means), который является усовершенствованной версией метода \(k\) средних для обработки больших массивов данных.
Отличие алгоритма, реализованного функцией ewkm() из одноименного пакета, заключается в вычислении весов, оценивающих меру относительной важности участия каждой переменной в формировании каждого кластера. Эти веса включаются в функцию расстояния, тем самым уменьшая его для более значимых переменных, и пересчитываются на каждой итерации объединения в кластеры.
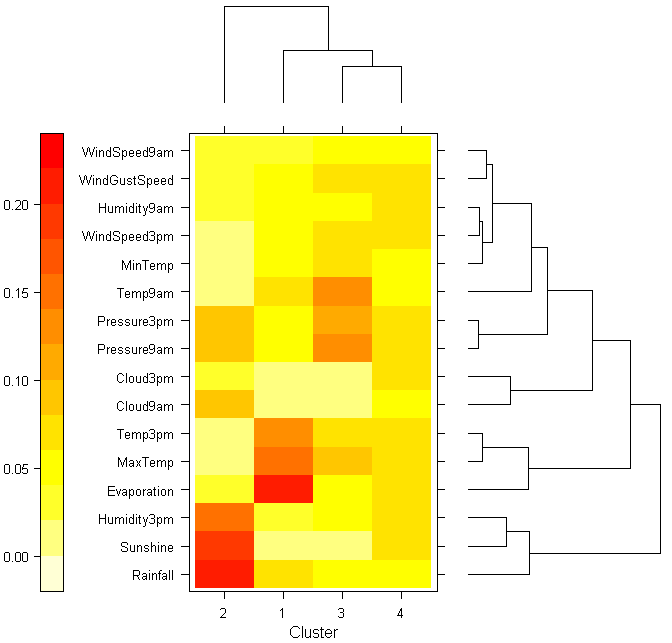
Нажатие кнопки Weights приводит к выводу весьма полезной диаграммы, которая для каждой переменной и каждого кластера показывает итоговые относительные веса в стиле “тепловой карты” (реализовано функцией levelplot() из пакета ewkm). Одновременно приведены дендрограммы иерархического объединения в группы как использованных переменных, так и исходных наблюдений, что облегчает проблему выбора числа кластеров.
Нажатие кнопки Discriminant выводит ординационную диаграмму с нанесенной структурой кластеров - продукт использования функции clusplot():
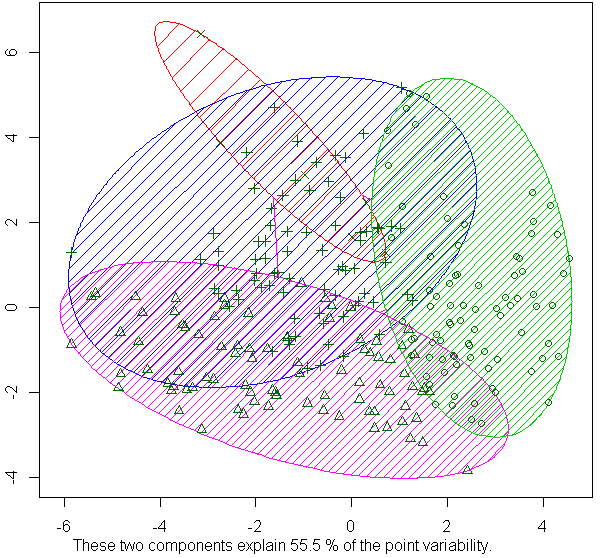
11.4.2 Ассоциативные правила
Подробно механизм формирования ассоциативных правил был рассмотрен нами в разделе 5.4. Здесь мы остановимся на небольшом примере распределения корзины товаров из 10 фильмов на DVD по заявкам 10 покупателей. Цель анализа - обнаружить закономерности формирования заявок.
Исходные данные загрузим из файла dvdtrans.csv, представленном на сайте разработчиков пакета rattle. Этот файл имеет следующую структуру:
ID,Item
1,Sixth Sense
1,LOTR1
1,Harry Potter1
1,Green Mile
1,LOTR2
2,Gladiator
2,Patriot
2,BraveheartК великому сожалению, русификация названий фильмов приводит к ошибке при выводе ассоциативных правил, поэтому нам придется знакомый всем “Властелин колец” скрывать под непонятной меткой "LOTR". После загрузки файла и нажатия кнопки Выполнить получаем итоги выполнения алгоритма "Apriory":
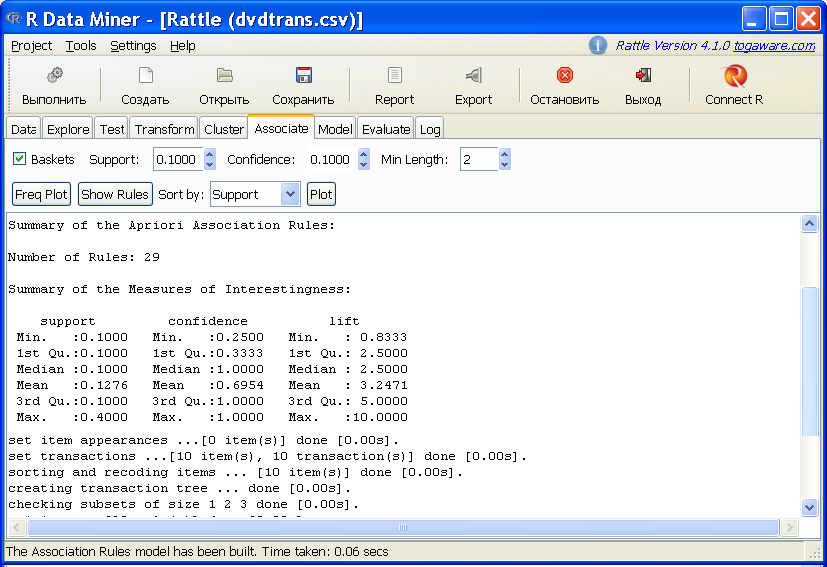
Опция Freq Plot выполняет визуализацию графика частотного распределения встречаемости комбинаций (см. рис. 5.4б). Опция Show Rules приводит к формированию списка найденных ассоциативных правил, отсортированных по уровню поддержки (Support):
All Rules
lhs rhs support confidence lift
[1] {Gladiator} => {Patriot} 0.4 1.0000000 2.5000000
[2] {Patriot} => {Gladiator} 0.4 1.0000000 2.5000000
[3] {LOTR1} => {LOTR2} 0.2 1.0000000 5.0000000
[4] {LOTR2} => {LOTR1} 0.2 1.0000000 5.0000000
[5] {Harry Potter1} => {Harry Potter2} 0.1 1.0000000 10.0000000
[6] {Harry Potter2} => {Harry Potter1} 0.1 1.0000000 10.0000000
... ... ...
[22] {Braveheart,Patriot} => {Gladiator} 0.1 1.0000000 2.5000000
[23] {Gladiator,Patriot} => {Braveheart} 0.1 0.2500000 2.5000000
[24] {LOTR1,LOTR2} => {Green Mile} 0.1 0.5000000 2.5000000
[25] {Green Mile,LOTR1} => {LOTR2} 0.1 1.0000000 5.0000000
[26] {Green Mile,LOTR2} => {LOTR1} 0.1 1.0000000 5.0000000
[27] {Gladiator,Sixth Sense} => {Patriot} 0.1 1.0000000 2.5000000
[28] {Patriot,Sixth Sense} => {Gladiator} 0.1 1.0000000 2.5000000
[29] {Gladiator,Patriot} => {Sixth Sense} 0.1 0.2500000 0.8333333Вполне понятно, что посмотревшие первую серию “Властелина колец” или “Гарри Поттера” будут, вероятно, смотреть и вторую, а любители “Гладиатора” и “Патриота” захотят ознакомиться и с “Храбрым сердцем”. Для аналитиков, склонных изучать большое количество разных индексов, пакет позволяет вывести дополнительную таблицу мер “интересности” правил:
Interesting Measures
chiSquared hyperLift hyperConfidence leverage oddsRatio phi
1 10.00000000 1.3333333 0.9952381 0.24 NA 1.00000000
2 10.00000000 1.3333333 0.9952381 0.24 NA 1.00000000
3 10.00000000 1.0000000 0.9777778 0.16 NA 1.00000000
4 10.00000000 1.0000000 0.9777778 0.16 NA 1.00000000
5 10.00000000 1.0000000 0.9000000 0.09 NA 1.00000000
6 10.00000000 1.0000000 0.9000000 0.09 NA 1.00000000
... ... ...
22 1.66666667 1.0000000 0.6000000 0.06 NA 0.40824829
23 1.66666667 1.0000000 0.6000000 0.06 NA 0.40824829
24 1.40625000 0.5000000 0.6222222 0.06 7.0000000 0.37500000
25 4.44444444 1.0000000 0.8000000 0.08 NA 0.66666667
26 4.44444444 1.0000000 0.8000000 0.08 NA 0.66666667
27 1.66666667 1.0000000 0.6000000 0.06 NA 0.40824829
28 1.66666667 1.0000000 0.6000000 0.06 NA 0.40824829
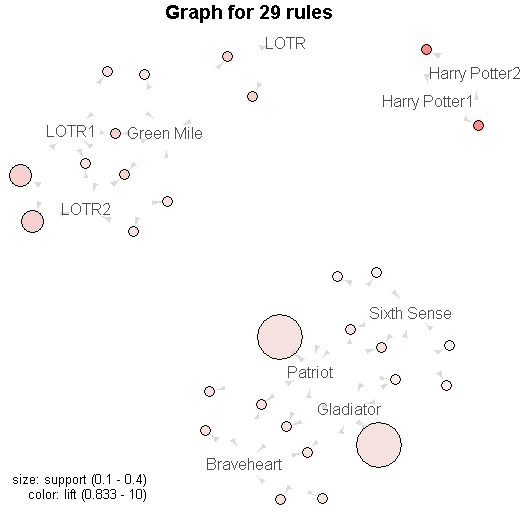
29 0.07936508 0.3333333 0.1666667 -0.02 0.6666667 -0.08908708Опция `` выводит знакомый нам по рис. 5.7 граф сформированных правил, где достаточно четко прослеживаются покупательские предпочтения: