ГЛАВА 2 Статистические модели: критерии и методы оценивания их качества
2.1 Основные шаги построения и верификации моделей
Построение и последующая проверка работоспособности полученных моделей представляет собой сложный и итеративный процесс, по итогам которого достигается приемлемый уровень уверенности исследователя в том, что результаты, получаемые с помощью итоговой модели, окажутся практически полезными. При этом выделяются следующие стандартные шаги (Kuhn, Johnson, 2013), которые мы будем подробно обсуждать далее:
- Разведочный анализ данных (exploratory data analysis), главная цель которого – изучение статистических свойств имеющихся в наличии выборок (распределение переменных, наличие выбросов, необходимость трансформации и др.) и выявление характера взаимосвязей между откликом и предикторами (Mount, Zumel, 2014).
Выбор методов построения моделей и спецификация систематической части последних. Например, модели типа “доза-эффект” в биологии на одном и том же исходном материале могут быть построены с использованием самых различных функций: логистической, экспоненциальной, Вейбулла, Гомперца, Михаелиса-Ментен, Брейна-Кузенса и т.д. (Шитиков, 2016).
Оценка параметров моделей и их диагностика (Мастицкий, Шитиков, 2014). Диагностика и оценка валидности (model validation) включает в себя ряд стандартных процедур. Так, в случае с классическими регрессионными моделями, подгоняемыми по методу наименьших квадратов, выполняются: а) проверка статистической значимости модели в целом и анализ неопределенности оцененных коэффициентов; б) проверка допущений в отношении остатков модели; в) обнаружение необычных наблюдений и выбросов; г) построение графиков, позволяющих оценить соответствие модели структуре анализируемых данных.
Анализ вклада отдельных предикторов и селекция оптимальной комбинации из них (model selection). Оценка качества каждой модели-претендента (model evaluation) по совокупности объективных критериев эффективности, включая тестирование на порции “свежих” данных, не участвовавших в процессе оценивания коэффициентов.
Ранжирование нескольких альтернативных моделей и, при необходимости, подстройка их важнейших параметров (model tuning). Рассматриваемые в этом разделе параметрические регрессионные модели в классическом представлении являются аппроксимацией математического ожидания отклика Y по обучающей выборке с помощью неизвестной функции регрессии \(f(\dots)\): \[E(Y | x_1, x_2, \dots, x_m) = f(\boldsymbol{\beta}, x_1, x_2, \dots, x_m) + \boldsymbol{\epsilon}, \]
где остатки \(\boldsymbol{\epsilon}\) отражают ошибку модели, т.е. необъяснимую случайную вариацию наблюдаемых значений зависимой переменной относительно ожидаемого среднего значения.
С практической точки зрения, тестирование таких моделей ставит своей задачей выявление следующих основных проблем их возможного использования:
- Смещение (bias), или систематическая ошибка модели (сдвиг предсказываемых значений на некоторую трудно объяснимую величину);
- Высокая случайная дисперсия прогноза, определяемая чаще всего излишней чувствительностью модели к небольшим изменениям в распределении обучающих данных;
- Неадекватность - тенденция модели не отражать основных закономерностей генеральной совокупности данных и основываться на случайных флуктуациях обучающей выборки;;
- Переусложнение модели (overfitting), которое “так же вредно, как и ее недоусложнение” (Ивахненко, 1982).
Действительно, для любого проверочного наблюдения \(x_0\) математическое ожидание среднеквадратичной ошибки его прогноза можно разложить на сумму трех величин: дисперсии \(f(x_0)\), квадрата смещения \(f(x_0)\) и дисперсии остатков \(\epsilon\) (подробнее см. James et al., 2013): \[ E[y_0 - f(x_0)]^2 = \text{Var}[f(x_0)] + [\text{Bias}(f(x_0))]^2 + \text{Var}(\epsilon), \]
где \(\text{Bias}\) означает смещение, а \(\text{Var}\) - дисперсию. Здесь мы предположили, что неизвестная истинная функция \(f(\dots)\) была оцененая на большом числе обучающих выборок, а отклонения \(y_0\) вычислялись по каждой из множества моделей с последующим усреднением результатов.
Из приведенного уравнения следует, что для минимизации ожидаемой ошибки прогноза мы должны подобрать такую модель, для которой одновременно достигаются низкое смещение и низкая дисперсия. Обратите внимание, что дисперсия никогда не может быть ниже некоторого уровня неустранимой ошибки \(\text{Var}(\epsilon)\).
Выше мы упомянули также феномен переусложнения модели, при котором наблюдается низкая дисперсия прогноза на обучающей совокупности, но часто получаются непредсказуемые результаты при тестировании блоков “свежих” данных, не участвоваших в построении модели.
В качестве простого примера используем данные по электрическому сопротивлению (Ом) мякоти фруктов киви в зависимости от процентного содержания в ней сока. Таблица с этими данными (fruitohms) входит в состав пакета DAAG, который является приложением к книге Maindonald (2010). В рассматриваемом примере у нас есть лишь один предиктор - содержание сока в мякоти фруктов juice, и было бы вполне логичным на первоначальном этапе рассмотреть простую линейную регрессию.
Для визуализации данных воспользуемся одним из лучших графических пакетов для R - ggplot2, который позволяет строить как всевозможные простые диаграммы рассеяния, так и гораздо более сложные графики, включающие, например, двумерные диаграммы распределения плотности (Мастицкий, 2016). Легко показать линию регрессии с ее доверительными интервалами, которые накрывают менее половины наблюдений (рис. 2.1):
library(DAAG)
data("fruitohms")
library(ggplot2)
ggplot(fruitohms, aes(x = juice, y = ohms)) +
geom_point() +
stat_smooth(method = "lm") +
xlab("Содержание сока, %") +
ylab("Сопротивление, Ом")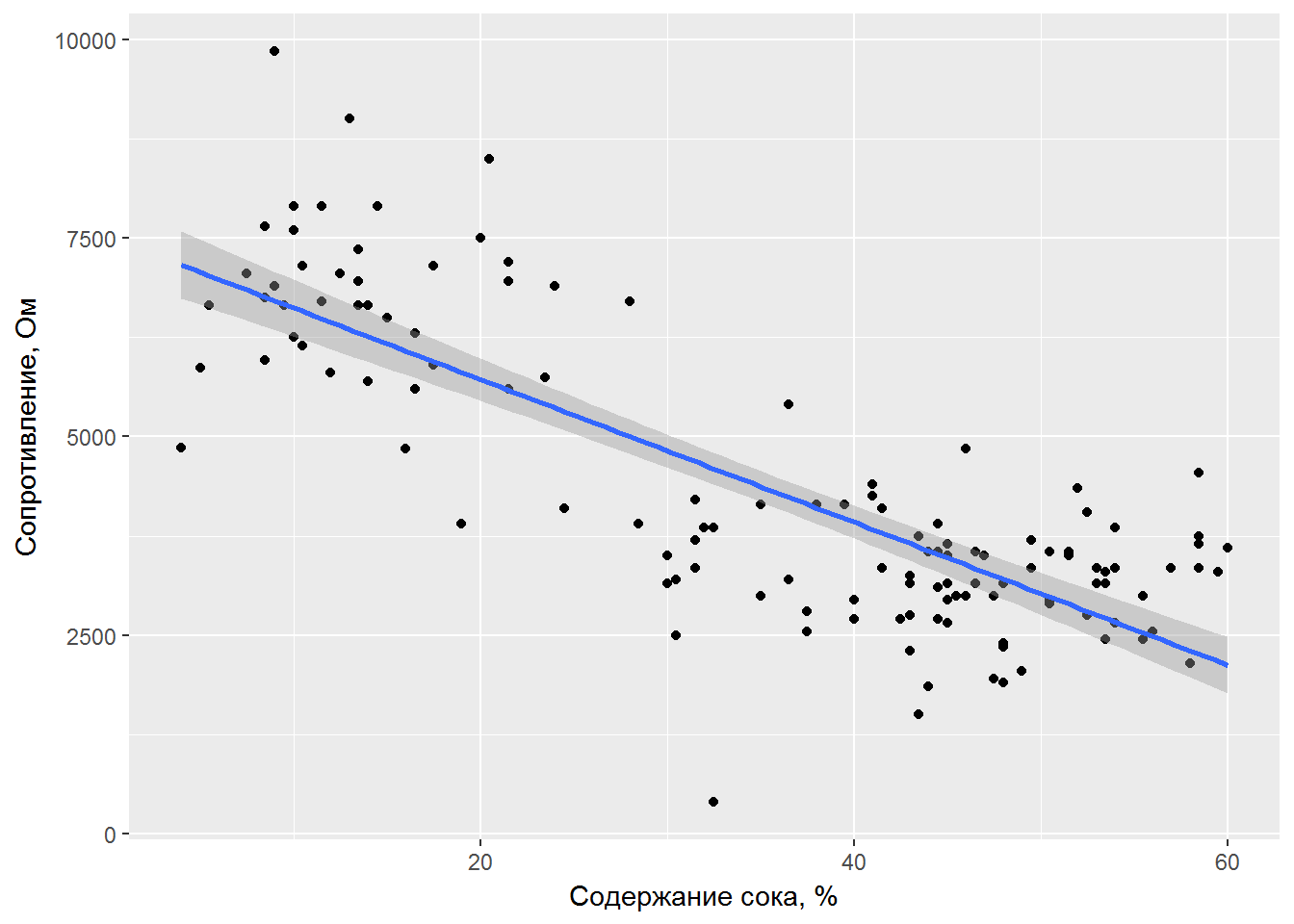
Рисунок 2.1: График линейной зависимости электрического сопротивления мякоти плодов киви от содержания сока
Все критерии оценки качества классических моделей регрессии f так или иначе основаны на анализе остатков (residuals), т.е. разностей между прогнозируемыми f(x[i,]) и наблюдаемыми y[i] значениями, где x - матрица независимых переменных. Базовыми критериями являются сумма квадратов остатков RSS (residual sum of squares), корень из среднеквадратичной ошибки RMSE (root mean square error) и стандартное отклонение остатков RSE (residual standard error). Для унификации в листингах кода перейдем от математических обозначений переменных к их формальным эквивалентам (y и x соответственно). Преобразуем заодно омы в килоомы, чтобы избежать слишком больших значений:
x <- fruitohms$juice
y <- fruitohms$ohms/1000
# Строим модель с одним предиктором:
n <- dim(as.matrix(x))[1]; m <- dim(as.matrix(x))[2]
M_reg <- lm(y ~ x); pred <- predict(M_reg)
# Рассчитываем критерии качества:
RSS <- sum((y - pred) * (y - pred))
RMSE <- sqrt(RSS/n)
RSE <- sqrt(RSS/(n - m - 1))
c(RSS, RMSE, RSE)## [1] 158.706891 1.113507 1.122309Мы не можем сказать с определенностью, малы или велики эти ошибки, поскольку все зависит от шкалы измерения y, и поэтому необходимо определиться с набором “эталонов” для сравнения. Тогда, выбрав некоторый подходящий критерий качества, мы сможем оценить, насколько эффективность тестируемой модели по этому критерию отличается от эталона. Такими эталонными моделями являются (Mount, Zumel, 2014):
- Нулевая модель, определяющая нижнюю границу качества. Если тестируемая модель значимо не превосходит по своей эффективности нулевую, то результат моделирования можно трактовать как неудачу. Обычно нуль-модель строится в соответствии с двумя принципами: а) она является независимой и не усматривает какой-либо связи между переменными и откликом, б) эквивалентна константе и дает на выходе один и тот же результат для всех возможных входов. Как правило, это среднее значение отклика для располагаемой выборки, либо наиболее популярная категория при классификации.
- Модель с минимальным уровнем байесовской ошибки (Bayes rate model) - самая лучшая модель для данных, имеющихся под рукой. Она, как правило, основывается на всех имеющихся переменных (т.е. является максимально “насыщенной” - saturated model) и ее ошибка определяется только набором наблюдений с разными значениями отклика y при одних и тех же \(x_1, x_2, \dots, x_n\). Если тестируемая модель по критерию эффективности значимо лучше нуль-модели и приближается к максимально насыщенной, то процесс селекции моделей можно считать завершенным.
- Модель с одной наиболее информативной переменной. Если в процессе селекции более сложные модели по своей эффективности не превосходят модель с одной переменной, то включение дополнительных переменных вряд ли имеет смысл.
Традиционными оценками качества аппроксимации данных является коэффициент детерминации Rsquared, дисперсионное отношение Фишера \(F\) и соответствующее ему \(p\)-значение. Отметим, что \(F\)-критерий интерпретируется как мера превышения точности предсказания отклика у построенной модели над нуль-моделью:
Rsquared <- 1 - RSS/sum((mean(y) - y)^2)
Fcr <- (sum((mean(y) - pred)^2)/m)/(RSS/(n - m - 1))
p <- pf(q = Fcr, df1 = m, df2 = (n - m - 1), lower.tail = FALSE)
c(Rsquared, Fcr, p)## [1] 6.387089e-01 2.227492e+02 1.234110e-29Разумеется, все эти величины можно получить и с помощью стандартной функции summary(), но нам показалось интересным показать всю “кухню” их расчетов.
summary(M_reg)##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.1984 -0.7939 0.0038 0.6143 3.1395
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.519404 0.233779 32.16 <2e-16 ***
## x -0.089877 0.006022 -14.93 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.122 on 126 degrees of freedom
## Multiple R-squared: 0.6387, Adjusted R-squared: 0.6358
## F-statistic: 222.7 on 1 and 126 DF, p-value: < 2.2e-16anova(M_reg)## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## x 1 280.57 280.57 222.75 < 2.2e-16 ***
## Residuals 126 158.71 1.26
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Мы убедились в том, что линейная модель со статистически значимыми коэффициентами по всем формальным критериям вполне адекватна полученным данным. Для проверки условия однородности дисперсии остатков в пакете car имеется функция ncvTest() (от “non-constant variance test” - “тест на непостоянную дисперсию”), которая позволяет проверить нулевую гипотезу о том, что дисперсия остатков никак не связана с предсказанными моделью значениями.
car::ncvTest(M_reg)## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 4.647123 Df = 1 p = 0.03110564Те же данные мы можем использовать для построения обобщенной линейной модели (general linear model, GLM), задав в качестве аргумента family функции glm() гауссовый характер распределения данных "gaussian". Вместо минимизации суммы квадратов отклонений эта модель ищет экстремум логарифма функции наибольшего правдоподобия (log maximum likelihood), вид которой зависит от заданного распределения.
В общем случае, значение функции правдоподобия численно равно вероятности того, что модель правильно предсказывает любое предъявленное ей наблюдение из заданной выборки. Логарифм функции правдоподобия LL будет всегда отрицательным, и, поскольку \(\log 1 = 0\), то для оптимальной модели, прогнозирующей наименее ошибочное значение отклика, значение LL будет стремиться к 0. Часто для оценки расхождений между наблюдаемыми и прогнозируемыми данными вместо LL используют остаточный девианс2 (deviance), который определен как D = -2(LL - S), где S – правдоподобие “насыщенной модели” с минимально возможным уровнем неустранимой ошибки. Обычно принимают S = 0, поскольку наилучшая модель выполняет, как правило, верное предсказание.
Чем меньше выборочный остаточный девианс D, тем лучше построенная модель. Аналогично можно рассчитать логарифм правдоподобия и девианс для нулевой модели D.null. Тогда адекватность модели определяется соотношением девианса остатков D и нуль-девианса D.null путем вычисления псевдо-коэффициента детерминации PRsquare. Девианс-анализ является обобщением техники дисперсионного анализа и статистическую значимость разности двух значений девианса (D.null – D) можно оценить по критерию \(\chi^2\):
M_glm <- glm(y ~ x)
lgLik <- logLik(M_glm)
D.null <- M_glm$null.deviance
D <- M_glm$deviance
df <- with(M_glm, df.null - df.residual)
p <- pchisq(D.null - D, df, lower.tail = FALSE)
PRsquare = 1 - D/D.null
c(lgLik, D, D.null, p, PRsquare)## [1] -1.953860e+02 1.587069e+02 4.392770e+02 5.641050e-63 6.387089e-01Те же величины можно получить с использованием функции summary():
summary(M_glm)##
## Call:
## glm(formula = y ~ x)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -4.1984 -0.7939 0.0038 0.6143 3.1395
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.519404 0.233779 32.16 <2e-16 ***
## x -0.089877 0.006022 -14.93 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 1.259579)
##
## Null deviance: 439.28 on 127 degrees of freedom
## Residual deviance: 158.71 on 126 degrees of freedom
## AIC: 396.77
##
## Number of Fisher Scoring iterations: 2with(M_glm, null.deviance - deviance)## [1] 280.5701anova(M_glm, glm(x ~ 1), test = "Chisq")## Analysis of Deviance Table
##
## Model: gaussian, link: identity
##
## Response: y
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 127 439.28
## x 1 280.57 126 158.71 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Нетрудно заметить, что классическая и обобщенная линейные модели в случае нормального распределения дают идентичные результаты и отличаются лишь по характеру используемой терминологии.
Рассмотрим теперь обоснованность выбора систематической части модели. Поверим утверждениям, что наиболее совершенным инструментом экспертизы нелинейности пока остается глаз человека, и отметим на рис. 2.1 некоторую асимметрию распределения точек относительно линии регрессии: в середине шкалы \(x\) модель имеет тенденцию к завышению значений \(y\), тогда как в области низких и высоких значений \(x\) наблюдается обратная тенденция.
Прекрасным способом оценить возможную нелинейность зависимости является использование кривых сглаживания, рассчитанных при помощи моделей локальной регрессии с использованием функции loess(), или сплайнов. Вместо обычного облака рассеяния точек покажем двумерную гистограмму hexbin (или “сотовую карту”), в которой данные распределены по ячейкам и число наблюдений в каждой ячейке представлено соответствующим оттенком цвета (рис. 2.2):
library(hexbin)
ggplot(fruitohms, aes(x = juice, y = ohms)) +
geom_hex(binwidth = c(3, 500)) +
geom_smooth(color = "red", se = FALSE) +
xlab("Содержание сока, %") +
ylab("Сопротивление, Ом")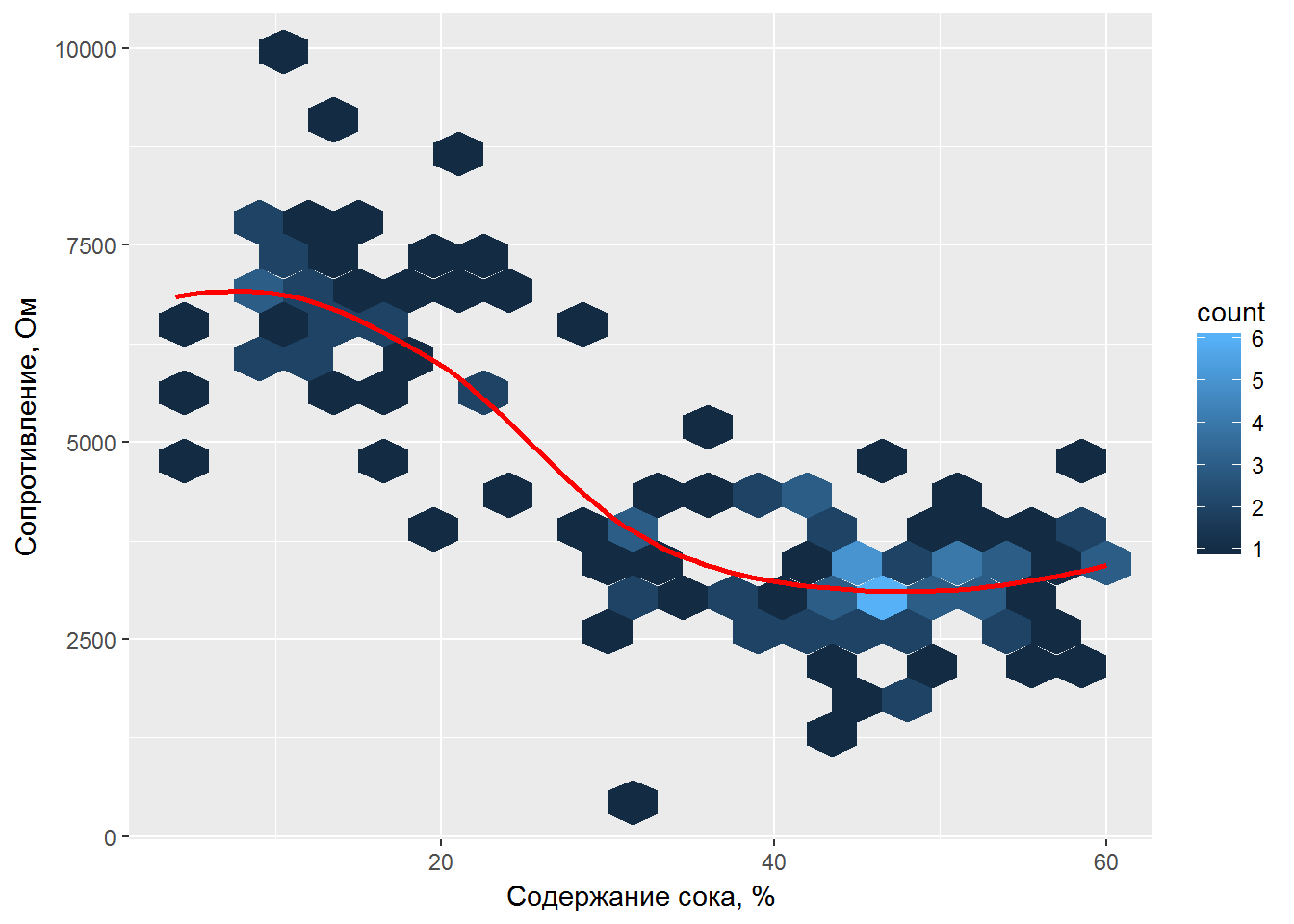
Рисунок 2.2: Кривая сглаживания зависимости электрического сопротивления мякоти плодов киви от содержания сока
Поскольку функциональная форма истинной модели нам неизвестна, сделаем предположение, что удовлетворительная аппроксимация данных может быть выполнена полиномиальной зависимостью. Отметим, что при увеличении степени m полинома любые критерии эффективности, основанные на остатках (RSE, Rsquared, F) будут монотонно улучшаться, поскольку каждая новая модель будет полнее отражать характер зависимости, имеющий место в обучающей выборке (рис. 2.3).
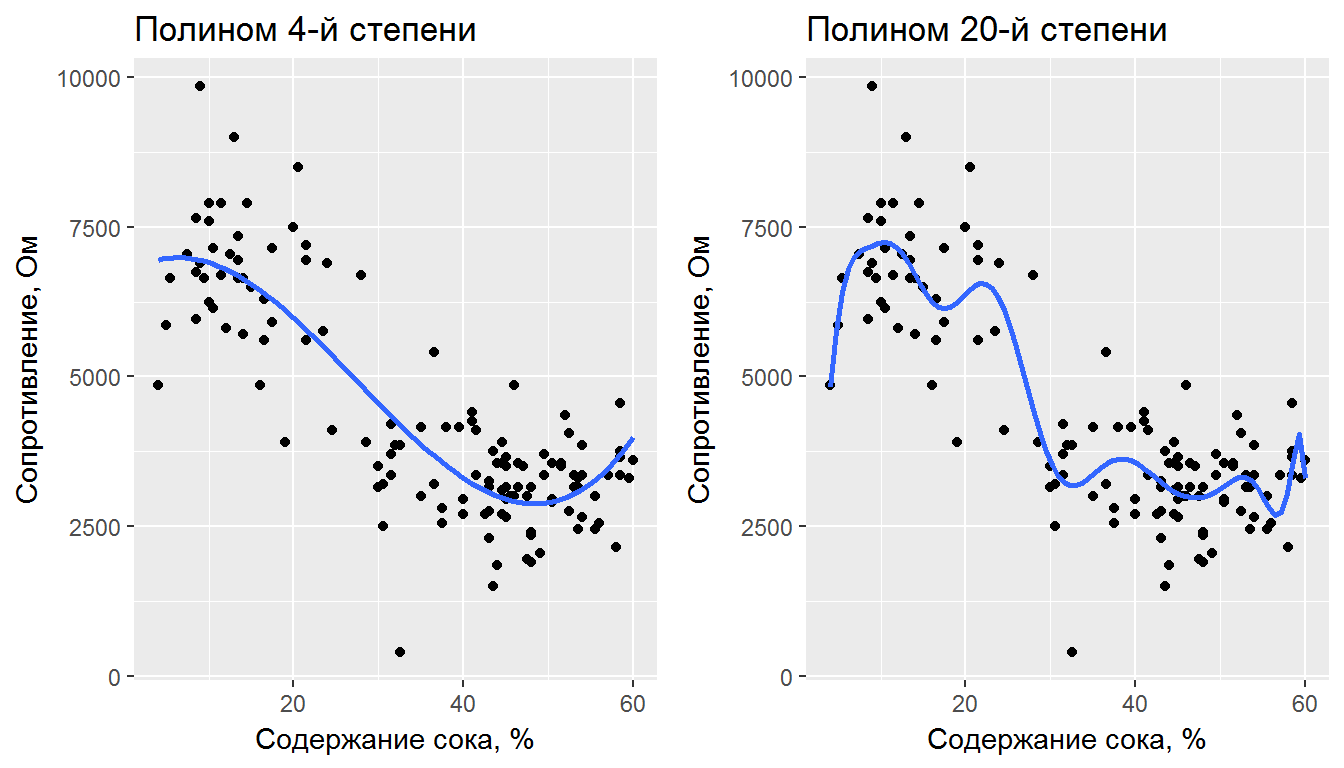
Рисунок 2.3: Аппроксимация данных полиномами разных степеней
Однако решение с минимально возможной ошибкой на обучающей выборке оказывается неоправданно сложным - аппроксимирующая функция старательно учитывает все случайные флуктуации измерений и не в состоянии отследить основную форму тренда. Такая ситуация называется переобучением модели и выражается она в том, что на новых независимых данных такие модели могут вести себя довольно непредсказуемым образом. Теряется обобщающая способность решения (model generalization), связанная как со способностью модели описать наиболее характерные закономерности изучаемого явления, так и с универсальной применимостью прогнозов к широкому множеству новых примеров. Поэтому построение модели оптимальной сложности, в которой сбалансированы точность и устойчивость прогноза, является фундаментальной задачей совершенствования методов моделирования.
Одним из путей поиска наилучшей аппроксимирующей функции является использование метода регуляризации, когда задача минимизации ошибки решается на основе критериев, налагающих “штраф” за увеличение сложности модели. Если D - выборочный остаточный девианс, k - число свободных параметров модели, а n - объем обучающей выборки, то можно определить семейство следующих весьма популярных критериев, которые обобщены под названием информационных (Burnham, Anderson, 2002):
- классический критерий Акаике:
AIC = D + 2*k; - байеслвский критерий Шварца:
BIC = D + k*ln(n); - скорректированный критерий Акаике:
AICс= AIC+2k(k+1)/(n-k-1).
При построении параметрических моделей с использованием функций R рассчитать эти критерии можно различными способами:
k <- extractAIC(M_glm)[1]
AIC <- extractAIC(M_glm)[2]
AIC <- AIC(M_glm)
AICc <- AIC(M_glm) + 2*k*(k + 1)/(n - k - 1)
BIC <- BIC(M_glm)
BIC <- AIC(M_glm, k = log(n))
c(AIC, AICc, BIC)## [1] 396.7719 396.8679 405.3280Оптимальной считается такая модель, которой соответствуют субэкстремальные значения критериев качества (например, минимум AIC). Рассмотрим пример использования информационных критериев для выбора оптимального числа параметров полиномиальной регрессии (рис. 2.4):
# Построение моделей со степенью полинома от 1 до 7
max.poly <- 7
# Создание пустой таблицы для хранения значений AIC и BIC,
# рассчитанных для всех моделей, и ее заполнение
AIC.BIC <- data.frame(criterion = c(rep("AIC", max.poly),
rep("BIC", max.poly)), value = numeric(max.poly*2),
degree = rep(1:max.poly, times = 2))
for (i in 1:max.poly) {
AIC.BIC[i, 2] <- AIC(lm(y ~ poly(x, i)))
AIC.BIC[i + max.poly, 2] <- BIC(lm(y ~ poly(x, i)))
}
# График AIC и BIC для разных степеней полинома
qplot(degree, value, data = AIC.BIC,
geom = "line", linetype = criterion) +
xlab("Степень полинома") + ylab("Значение критерия")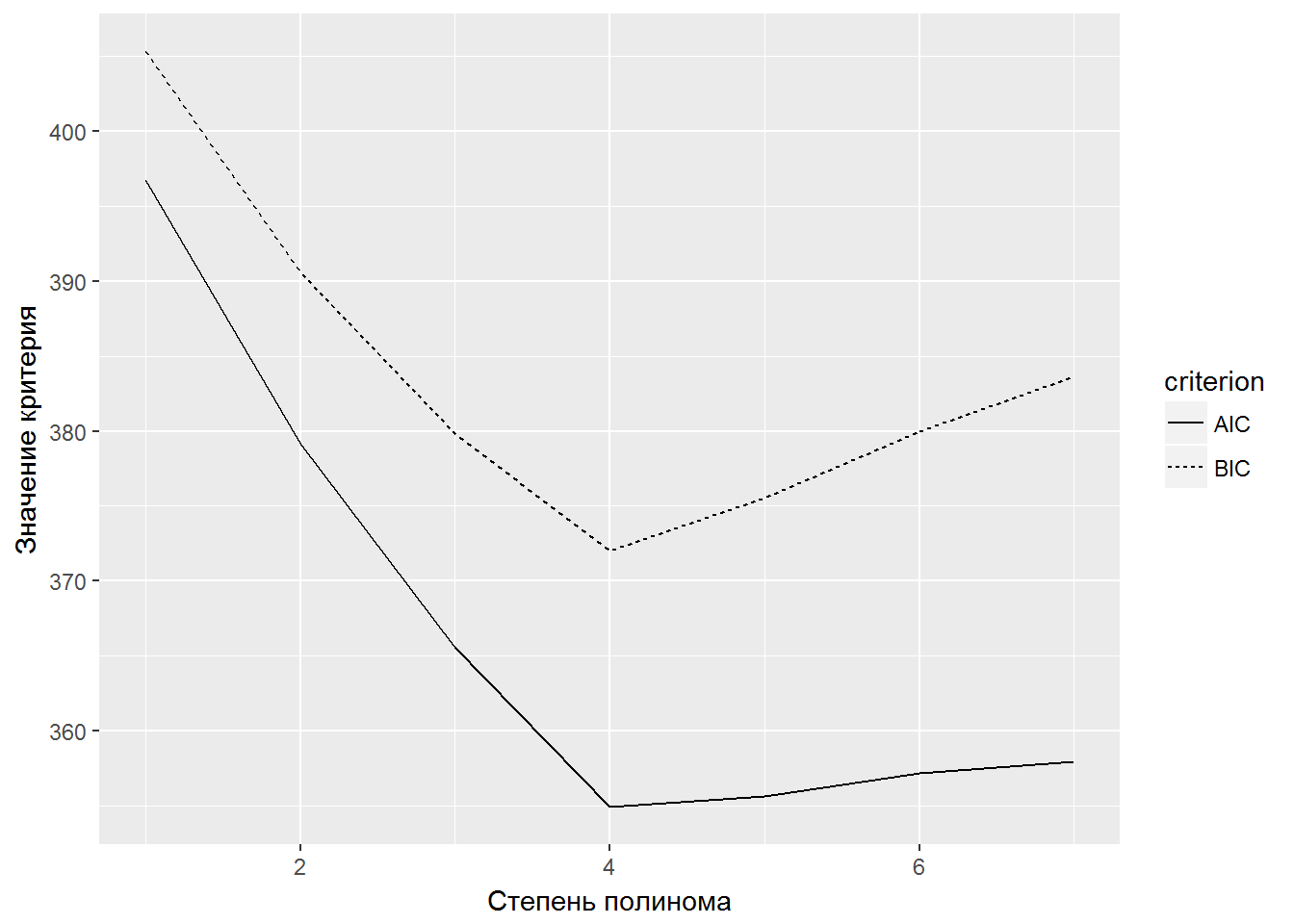
Рисунок 2.4: Поиск оптимальной степени полинома с использованием информационных критериев
Минимальные значения информационных критериев соответствуют выводу, что наилучшая модель - полином 4-й степени.
Этот термин в русскоязычной литературе пока не устоялся: используются также девиация (Ллойд, Ледерман, 1990) и аномалия (International Statistical Institute)↩