ГЛАВА 10 Кластерный анализ

10.1 Алгоритмы кластеризации, основанные на разделении

Алгоритмы неиерахического разделения (Partitioning algorithms) осуществляют декомпозицию набора данных, состоящего из \(n\) наблюдений, на \(k\) групп (кластеров) с заранее неизвестными параметрами. При этом выполняется поиск центроидов - максимально удаленных друг от друга центров сгущений точек \(C_k\) с минимальным разбросом внутри каждого кластера. К разделяющим алгоритмам относятся:

  • метод \(k\) средних Мак-Кина (\(k\)-means clustering; MacQueen, 1967), в котором каждый из \(k\) кластеров представлен центроидом;
  • разделение вокруг \(k\) медоидов или PAM (Partitioning Around Medoids; Kaufman, Rousseeuw, 1990), где медоид - это центроид, координаты которого смещены к ближайшему из исходных объектов данных;
  • алгоритм CLARA (Clustering Large Applications) - метод, весьма похожий на PAM и используемый для анализа больших наборов данных.

Метод \(k\) средних выполняет кластеризацию следующим образом:

  1. Назначается число групп (\(k\)), на которые должны быть разбиты данные. Случайно выбирается \(k\) объектов исходного набора как первоначальные центры кластеров.
  2. Каждому наблюдению присваивается номер группы по самому близкому центроиду, т.е. на основании наименьшего евклидова расстояния между объектом и точкой \(C_k\).
  3. Пересчитываются координаты центроидов \(\mu_k\) всех \(k\) кластеров и вычисляются внутригрупповые разбросы (within-cluster variation) \(W(C_k) = \sum_{x_i \in C_k} (x_i - \mu_k)^2\). Если набор данных включает \(р\) переменных, то \(\mu_k\) представляет собой вектор средних с \(p\) элементами.
  4. Минимизируется общий внутригрупповой разброс \(W_{total} = \sum_k W(C_k) \rightarrow \min\), для чего шаги 2 и 3 повторяются многократно, пока назначения групп не прекращают изменяться или не достигнуто заданное число итераций iter.max. Предельное число итераций для минимизации \(W_{total}\), установленное функцией kmeans() по умолчанию, составляет iter.max = 10.

В разделе 2.6 мы уже подробно разбирали пример кластеризации 50 штатов США по криминогенной обстановке на 5 групп с использованием функции kmeans() из пакета cluster. Пример сопровождается скриптами, графической интерпретацией разбиения и приводятся конкретные вычисленные значения вышеприведенных статистик. В связи с этим в дальнейшем мы будем обсуждать только нюансы практического использования метода.

Объединение в кластеры методом \(k\) средних - очень простой и эффективный алгоритм, имеющий, однако, две существенные проблемы. Во-первых, итоговые результаты чувствительны к начальному случайному выбору центров групп. Возможное решение этой проблемы состоит в многократном выполнении алгоритма с различным случайным назначением начальных центроидов. Итерация с минимальным значением \(W_{total}\) отбирается как конечный вариант кластеризации. Число таких итераций можно задать параметром nstart функции kmeans():

library(cluster)
data("USArrests")
df.stand <- as.data.frame(scale(USArrests))
set.seed(5)
c(kmeans(df.stand, centers = 5, nstart = 1)$tot.withinss,
  kmeans(df.stand, centers = 5, nstart = 25)$tot.withinss) 
## [1] 51.63029 48.94420

Нам удалось за 25 повторов алгоритма несколько уменьшить значение критерия оптимальности. Вторая проблема - необходимость априори задавать фиксированное число кластеров для разбиения, которое, безусловно, далеко не всегда выбирается оптимальным. Поэтому одной из задач кластерного анализа является подбор оптимального значения \(k\), для которой существует несколько версий решения. Метод “локтя” (elbow method) рассматривает характер изменения разброса \(W_{total}\) с увеличением числа групп \(k\). Объединив все \(n\) наблюдений в одну группу, мы имеем наибольшую внутрикластерную дисперсию, которая будет снижаться до 0 при \(k \rightarrow n\). На каком-то этапе можно усмотреть, что снижение этой дисперсии замедляется - на графике это происходит в точке, называемой “локтем” (родственник “каменистой осыпи” для анализа главных компонент). Построить такой график можно в результате прямого перебора, либо с использованием функции fviz_nbclust() из прекрасного пакета factoextra, предназначенного для визуализации результатов кластерного анализа на основе графической системы ggplot2:

k.max <- 15 # максимальное число кластеров
wss <- sapply(1:k.max, function(k){
    kmeans(df.stand, k, nstart = 10)$tot.withinss
})
# Вывод не приводится:
# plot(1:k.max, wss, type = "b", pch = 19, frame = FALSE, 
#      xlab = "Число кластеров K", 
#      ylab = "Общая внутригрупповая сумма квадратов")

# Формируем график с помощью fviz_nbclust():
library(factoextra)
fviz_nbclust(df.stand, kmeans, method = "wss") +
    geom_vline(xintercept = 4, linetype = 2)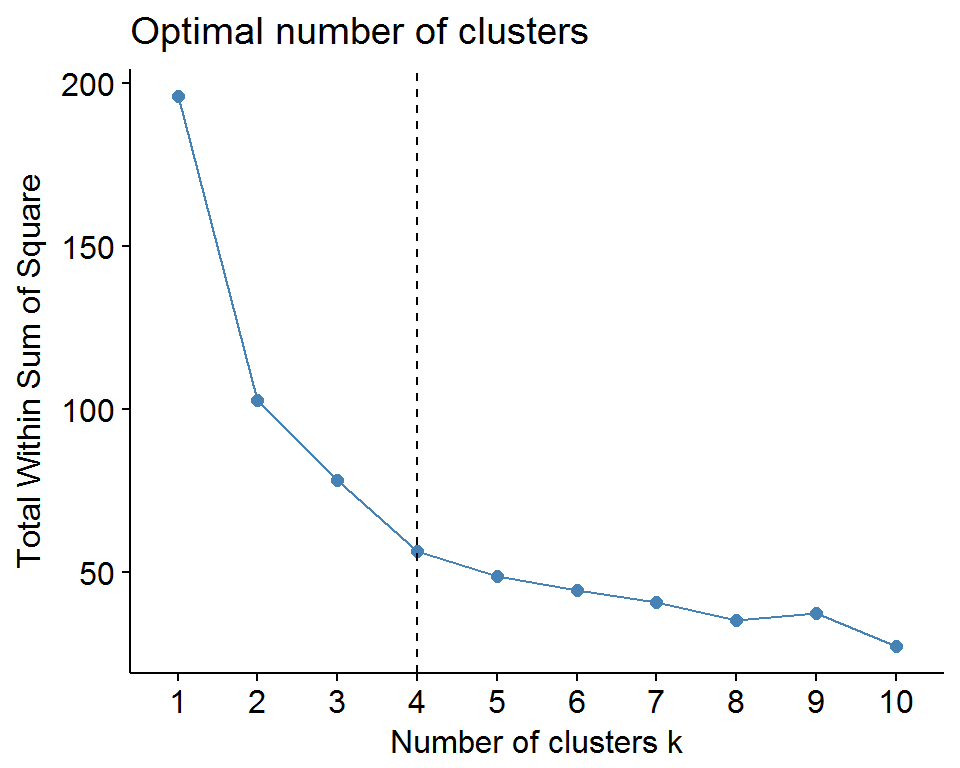
Выбор оптимального числа кластеров по методу "локтя"

Рисунок 10.1: Выбор оптимального числа кластеров по методу “локтя”

Альтернативой субъективно понимаемым графикам “локтя” является использование статистики разрыва (gap statistic; Tibshirani et al., 2001), которые генерируются на основе ресэмплинга и имитационных процедур Монте-Карло. Пусть \(E_{n}^*\{\log(W_k^*)\}\) обозначает оценку средней дисперсии \(W_k^*\), полученной бутстреп-методом, когда \(k\) кластеров образованы случайными наборами объектов из исходной выборки размером \(n\). Тогда статистика

\[Gap_{n}(k) = E_n^*\{\log(W_k^*)\} - \log(W_k)\]

определяет отклонение наблюдаемой дисперсии \(W_k\) от ее ожидаемой величины при справедливости нулевой гипотезы о том, что исходные данные образуют только один кластер.

При сравнительном анализе последовательности значений \(Gap_n(k), \, k = 2, \dots, K_{max}\) наибольшее значение статистики соответствует наиболее полезной группировке, дисперсия которой максимально меньше внутригрупповой дисперсии кластеров, собранных из случайных объектов исходной выборки:

set.seed(123)
gap_stat <- clusGap(df.stand, FUN = kmeans, nstart = 10, K.max = 10, B = 50)
# Печать и визуализация результатов
print(gap_stat, method = "firstmax")
## Clustering Gap statistic ["clusGap"] from call:
## clusGap(x = df.stand, FUNcluster = kmeans, K.max = 10, B = 50,     nstart = 10)
## B=50 simulated reference sets, k = 1..10; spaceH0="scaledPCA"
##  --> Number of clusters (method 'firstmax'): 4
##           logW   E.logW       gap     SE.sim
##  [1,] 3.458369 3.633279 0.1749100 0.04956376
##  [2,] 3.135112 3.370352 0.2352405 0.04192860
##  [3,] 2.977727 3.234819 0.2570927 0.04085179
##  [4,] 2.826221 3.120886 0.2946656 0.04153549
##  [5,] 2.738868 3.022296 0.2834282 0.04377128
##  [6,] 2.669860 2.935234 0.2653739 0.04201917
##  [7,] 2.612957 2.855663 0.2427060 0.04029606
##  [8,] 2.545027 2.782767 0.2377398 0.04031744
##  [9,] 2.471474 2.715964 0.2444898 0.03998257
## [10,] 2.397200 2.654907 0.2577068 0.04074831
fviz_gap_stat(gap_stat)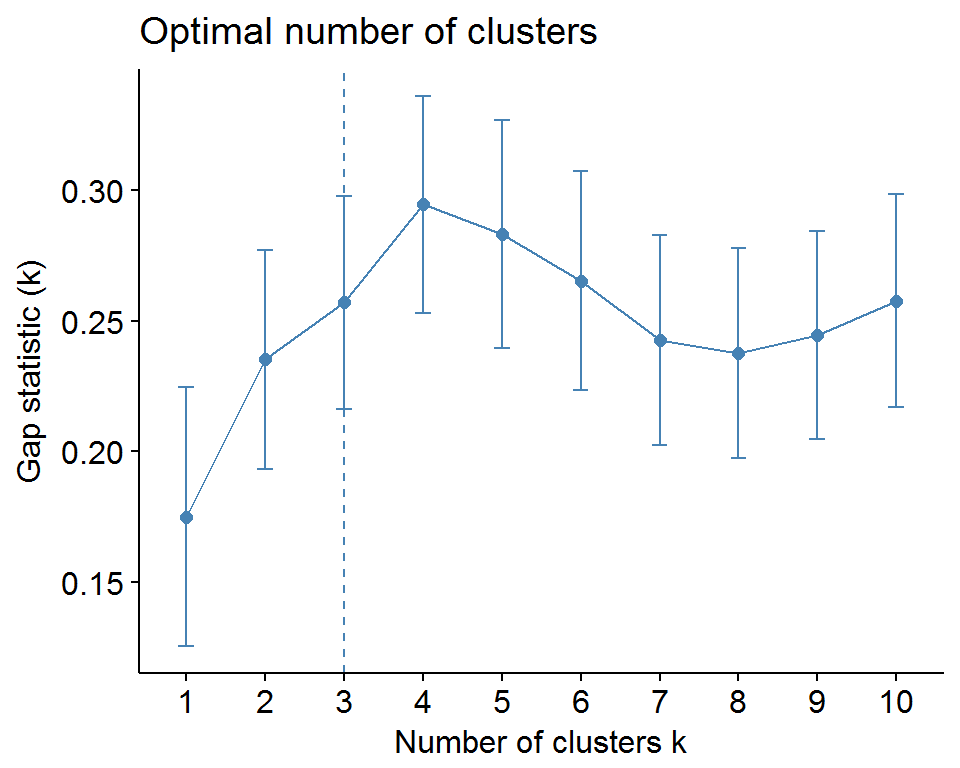
График GAP-статистики для выбора оптимального числа кластеров

Рисунок 10.2: График GAP-статистики для выбора оптимального числа кластеров

Параметр FUNcluster использованной выше функции clusGap() указывает на необходимый метод кластеризации и при FUN = pam осуществляется разделение вокруг \(k\) медоидов:

set.seed(123)
gap_stat <- clusGap(df.stand, FUN =  pam, K.max = 7, B = 100)
print(gap_stat, method = "firstmax")
## Clustering Gap statistic ["clusGap"] from call:
## clusGap(x = df.stand, FUNcluster = pam, K.max = 7, B = 100)
## B=100 simulated reference sets, k = 1..7; spaceH0="scaledPCA"
##  --> Number of clusters (method 'firstmax'): 4
##          logW   E.logW       gap     SE.sim
## [1,] 3.458369 3.632850 0.1744804 0.03737864
## [2,] 3.135112 3.380017 0.2449056 0.04476136
## [3,] 2.981802 3.250681 0.2688793 0.04601583
## [4,] 2.834744 3.141994 0.3072506 0.04709690
## [5,] 2.745099 3.049445 0.3043454 0.04729300
## [6,] 2.685908 2.962081 0.2761727 0.04687566
## [7,] 2.634287 2.886058 0.2517713 0.04560393
(k.pam <- pam(df.stand, k = 4))
## Medoids:
##               ID     Murder    Assault   UrbanPop         Rape
## Alabama        1  1.2425641  0.7828393 -0.5209066 -0.003416473
## Michigan      22  0.9900104  1.0108275  0.5844655  1.480613993
## Oklahoma      36 -0.2727580 -0.2371077  0.1699510 -0.131534211
## New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419
## Clustering vector:
##        Alabama         Alaska        Arizona       Arkansas     California 
##              1              2              2              1              2 
##       Colorado    Connecticut       Delaware        Florida        Georgia 
##              2              3              3              2              1 
##         Hawaii          Idaho       Illinois        Indiana           Iowa 
##              3              4              2              3              4 
##         Kansas       Kentucky      Louisiana          Maine       Maryland 
##              3              3              1              4              2 
##  Massachusetts       Michigan      Minnesota    Mississippi       Missouri 
##              3              2              4              1              3 
##        Montana       Nebraska         Nevada  New Hampshire     New Jersey 
##              3              3              2              4              3 
##     New Mexico       New York North Carolina   North Dakota           Ohio 
##              2              2              1              4              3 
##       Oklahoma         Oregon   Pennsylvania   Rhode Island South Carolina 
##              3              3              3              3              1 
##   South Dakota      Tennessee          Texas           Utah        Vermont 
##              4              1              2              3              4 
##       Virginia     Washington  West Virginia      Wisconsin        Wyoming 
##              3              3              4              4              3 
## Objective function:
##    build     swap 
## 1.035116 1.027102 
## 
## Available components:
##  [1] "medoids"    "id.med"     "clustering" "objective"  "isolation" 
##  [6] "clusinfo"   "silinfo"    "diss"       "call"       "data"

Метод PAM во многом идентичен алгоритму \(k\) средних за исключением того, что вместо вычисления центроидов осуществляется поиск \(k\) наиболее представительных объектов (или медоидов) среди анализируемых наблюдений. Внутрикластерный разброс оценивается при этом по манхэттенскому, а не евклидовому расстоянию, как в kmeans(). Мы прибегли к простейшему варианту вычислений - использованию функции pam() из пакета cluster, которая выделила в качестве центральных представителей классов Алабаму, Мичиган, Оклахому и Нью-Гэмпшир.

Поскольку параметром функции pam() также является число кластеров \(k\), проверим оптимальность его значения третьим из наиболее популярных методов - по средней ширине силуэта (average silhouette width). Для каждого найденного кластера может быть вычислена “ширина силуэта”:

\[s_i = \frac{b(i) - a(i)}{\max[b(i), a(i)]},\]

где \(a(i)\) - среднее расстояние между объектами \(i\)-го кластера, \(b(i)\) - среднее расстояние от объектов \(i\)-го кластера до другого кластера, самого близкого к \(i\)-му. Диаграмму силуэтов можно построить с использованием функции fviz_silhouette() из пакета factoextra:

fviz_silhouette(silhouette(k.pam))
##   cluster size ave.sil.width
## 1       1    8          0.39
## 2       2   12          0.31
## 3       3   20          0.28
## 4       4   10          0.46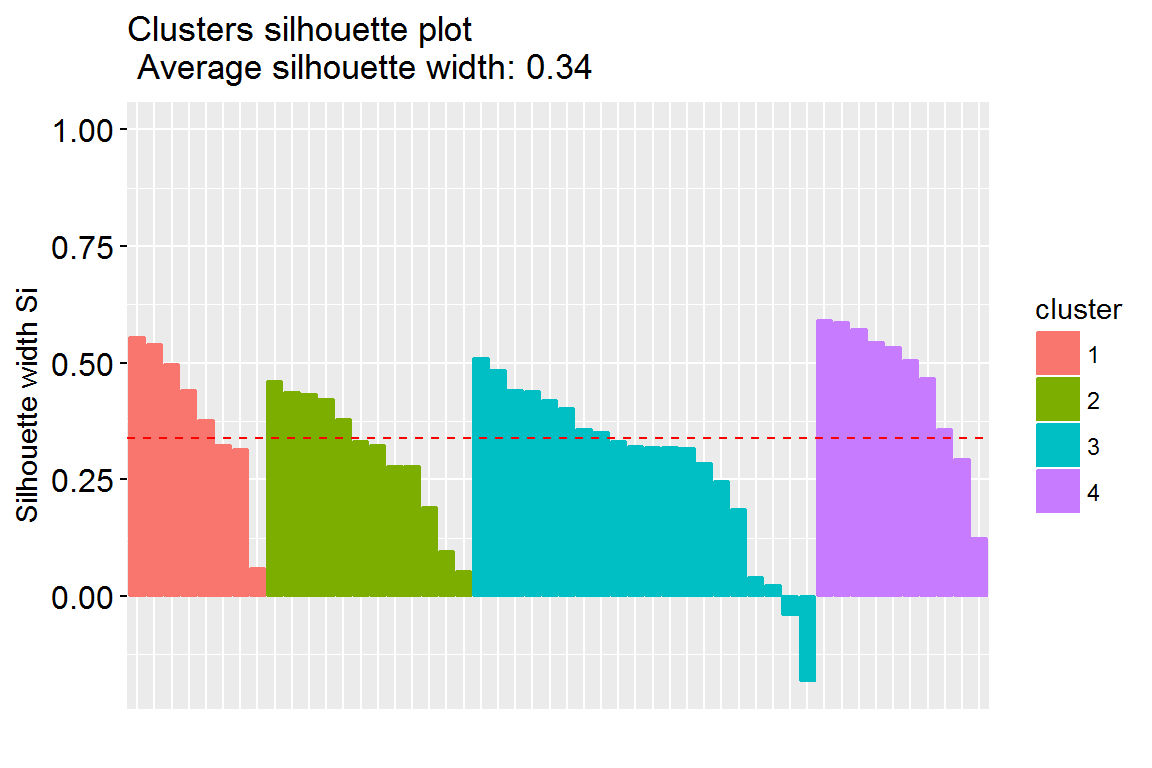
Диаграмма силуэтов при разбиении на 4 кластера

Рисунок 10.3: Диаграмма силуэтов при разбиении на 4 кластера

На рис. 10.3 для каждого из 50 штатов показана разность \(s\) средних расстояний до объектов своего кластера и чужого кластера, ближайшего к анализируемому объекту. Общее среднее из этих значений Smean определяет качество выполненной кластеризации. Функция fviz_nbclust() выполняет сканирование разбиений с различными значениями \(k\), и строит график зависимости \(S_{mean}\) от \(k\), подобный представленным на рис. 10.1-10.2.

fviz_nbclust(df.stand, pam, method = "silhouette")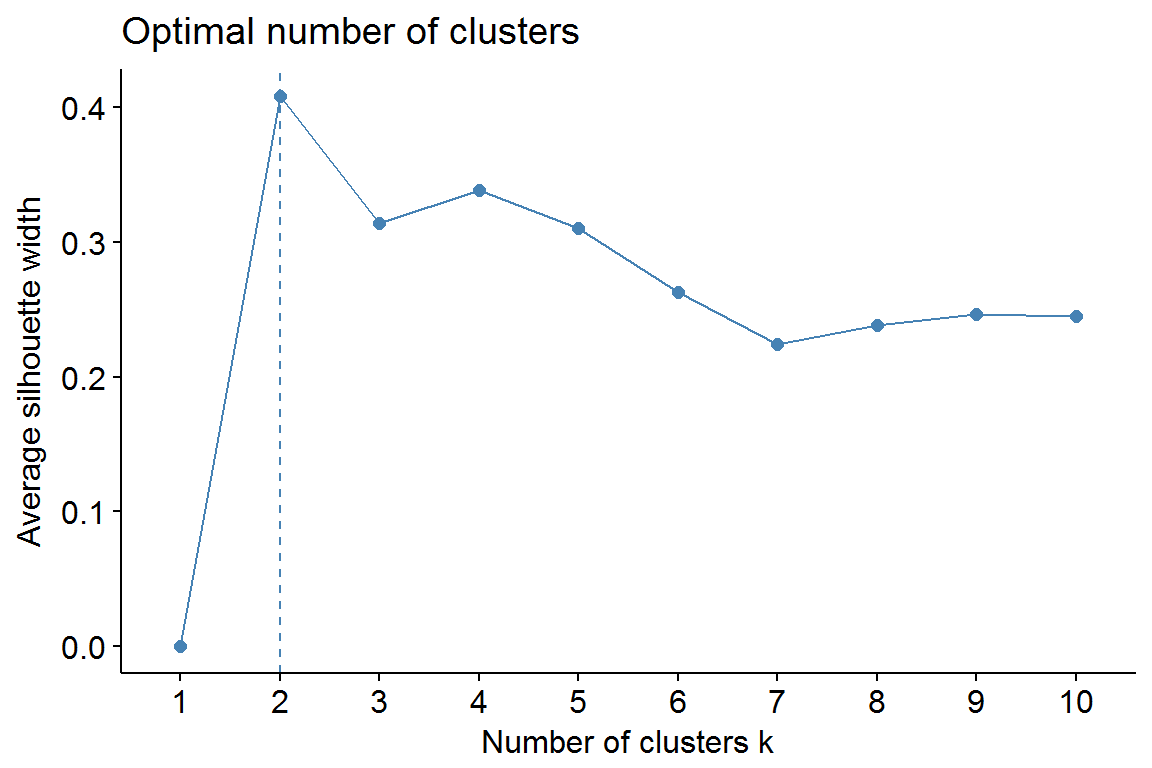
График ширины силуэтов для выбора оптимального числа кластеров

Рисунок 10.4: График ширины силуэтов для выбора оптимального числа кластеров

Метод силуэтов оценил как наилучшее разбиение на два кластера \(k = 2\). Отметим, что в условиях неопределенности различные алгоритмы могут порождать конкурирующие решения. Колеблющийся читатель может в таких случаях пользоваться функцией pamk() из пакета fpc, которая не требует задавать число классов, а оценивает его самостоятельно.

Алгоритм CLARA мало чем отличается от метода PAM, но приспособлен для обработки больших массивов данных (миллионы наблюдений и более). Соответствующая функция clara() из пакета cluster специально оптимизирована для сокращения времени расчетов и рационального использования оперативной памяти.

Значительный интерес представляет построение двумерных диаграмм (ординационных “биплотов”) распределения наблюдений по кластерам, которые формируются с предварительным приведением исходного пространства признаков к двум главным компонентам (см. рис. 2.13 из раздела 2.6). Обычно для этого используется функция clustplot(), но мы предлагаем вниманию читателей функцию fviz_cluster() из пакета factoextra, которая использует для создания диаграмм графическую систему ggplot2.

Эта функция может быть использована для визуализации результатов по методам \(k\) средних, PAM, CLARA и Fanny. Ее простейший формат имеет вид:

fviz_cluster(object, data = NULL, stand = TRUE, 
             geom = c("point", "text"), 
             frame = TRUE, frame.type = "convex")

где:

  • object: объект класса "partition", созданный функциями pam(), clara() или fanny() из пакета cluster, или объект, возвращаемый функцией kmeans();
  • data: таблица с исходными данными для кластеризации (этот аргумент необходим только, если используется объект kmeans);
  • stand = TRUE: данные стандартизуются перед выполнением анализа главных компонент;
  • geom: три возможных комбинации стиля отображения наблюдений на графике - текстовые метки "text", точки "point" или оба типа одновременно c("point", "text");
  • frame = TRUE: проводится контур вокруг точек для каждого кластера;
  • frame.type: возможные значения - "convex" или типы эллипсов ggplot2::stat_ellipse, включая один из трех c("t", "norm", "euclid").

Построим ординационные диаграммы для результатов кластеризации методами PAM и CLARA. Чтобы получить аккуратные графики, заменим длинные названия штатов США на их сокращенную аббревиатуру из файла St_USA.txt. Во втором случае будем использовать для построения эллипсов многомерное \(t\)-распределение с доверительным интервалом \(\eta = 0.7\):

ShState <- read.delim("data/St_USA.txt")
rownames(df.stand) <- ShState$Short
fviz_cluster(pam(df.stand, 4), stand = FALSE)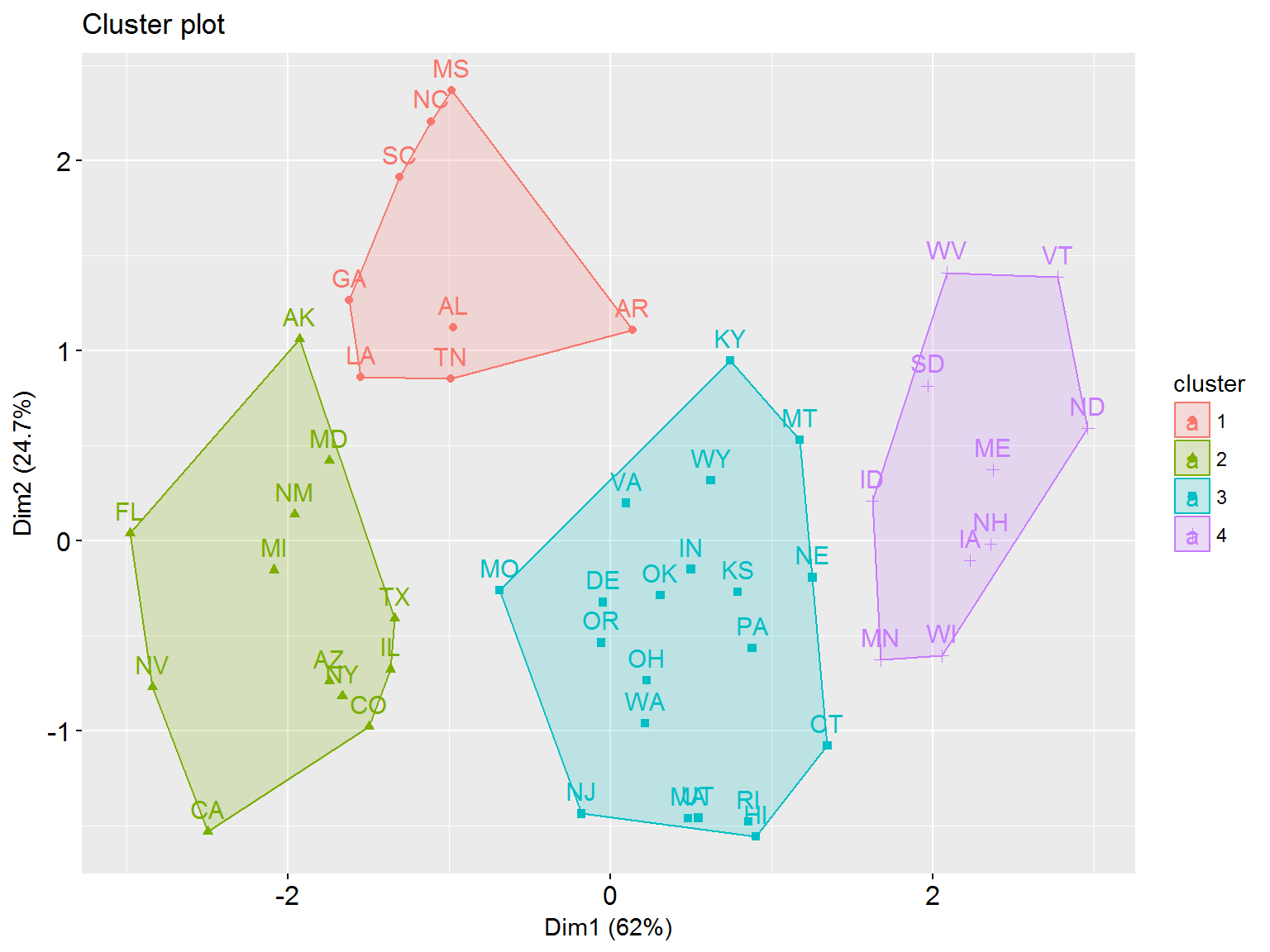
Диаграмма распределения штатов США по кластерам, полученным методом PAM

Рисунок 10.5: Диаграмма распределения штатов США по кластерам, полученным методом PAM 

fviz_cluster(clara(df.stand, 4), stand = FALSE, 
             ellipse.type = "t", ellipse.level = 0.7)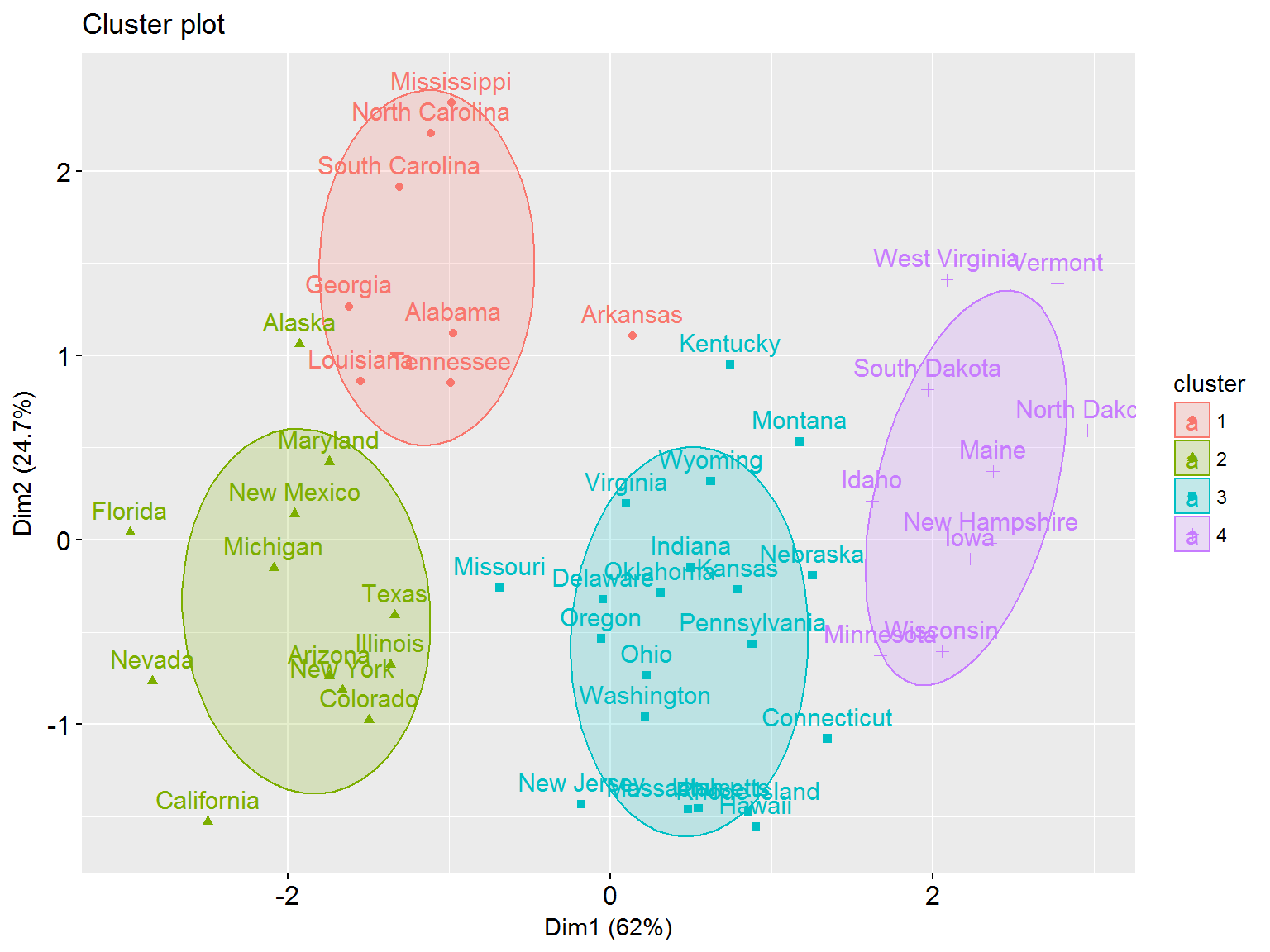
Диаграмма распределения штатов США по кластерам, полученным методом CLARA; эллипсы построены на основе $t$-распределения

Рисунок 10.6: Диаграмма распределения штатов США по кластерам, полученным методом CLARA; эллипсы построены на основе \(t\)-распределения