4.4 Ансамбли моделей: бэггинг, случайные леса, бустинг

В статистике хорошо известно интуитивное соображение, согласно которому усреднение результатов наблюдений может дать более устойчивую и надежную оценку, поскольку ослабляется влияние случайных флуктуаций в отдельном измерении. На аналогичной идее было основано развитие алгоритмов комбинирования моделей, в результате чего построение их ансамблей оказалось одним из самых мощных методов машинного обучения, нередко превосходящим по качеству предсказаний другие методы.

Одним из решений, обеспечивающих необходимое разнообразие моделей, является их повторное обучение на выборках, случайно выбранных из генеральной совокупности, либо иных подмножествах данных, сконструированных из имеющихся (рис. 4.14). Для получения устойчивого прогноза частные предсказания этих моделей тем или иным образом комбинируют, например, с помощью простого усреднения или голосования (возможно, взвешенного).

Ансамбль из пяти линейных классификаторов: каждый сегмент пространства объектов отличается средними вероятностями предсказания классов (подробности см. Флах, 2015, с. 344)

Рисунок 4.14: Ансамбль из пяти линейных классификаторов: каждый сегмент пространства объектов отличается средними вероятностями предсказания классов (подробности см. Флах, 2015, с. 344)

В разделе 2.2 был описан бутстреп - процедура генерации повторных случайных выборок из исходного набора данных. Бутстреп-выборки производятся равномерно и с возвращением, поэтому некоторые исходные примеры будут отсутствовать, а другие - дублироваться: в среднем одна такая выборка содержит около 2/3 уникальных исходных наблюдений.

4.4.1 Бэггинг и случайные леса

Бутстреп при формировании ансамбля моделей оказался особенно полезен в сочетании с древовидными структурами, которые очень чувствительны к небольшому изменению обучающих данных. Описанные в предыдущем разделе деревья решений обычно имеют низкое смещение, но страдают от высокой дисперсии. Это означает, что если мы случайным образом разобьем обучающие данные на две части и построим дерево решений на основе каждой из них, то полученные результаты могут оказаться довольно разными.

Подобно тому, как усреднение нескольких наблюдений снижает оценку дисперсии данных, так и разумным способом снижения дисперсии прогноза является извлечение большого количества порций данных из генеральной совокупности, построение предсказательной модели по каждой обучающей выборке и усреднение полученных предсказаний. Если вместо отдельных обучающих выборок (которых нам, как правило, всегда не хватает) выполнить бутстреп и на основе сгенерированных псевдо-выборок построить В деревьев регрессии, то средний коллективный прогноз

\[\hat{f}_{bag} = \left( f^1(x) + f^2(x) + \dots + f^B(x)\right) / B\]

будет обладать более низкой дисперсией. Эта процедура и называется бэггингом (сокр. от bootstrap aggregating). Как нами будет показано в последующих главах, бэггинг можно проводить не только в отношении деревьев регрессии, но и иных моделей: опорных векторов, линейных дискриминантов, байесовских вероятностей и др.

Метод случайного леса (Random Forest) представляет собой дальнейшее улучшение бэггинга деревьев решений, которое заключается в устранении корреляции между деревьями. Как и в случае с бэггингом, мы строим несколько сотен деревьев решений по обучающим бутстреп-выборкам. Однако на каждой итерации построения дерева случайным образом выбирается \(m\) из \(p\) подлежащих рассмотрению предикторов и разбиение разрешается выполнять только по одной из \(m\) этих переменных.

Смысл этой процедуры, оказавшейся весьма эффективной для повышения качества получаемых решений, заключается в том, что с вероятностью \((p - m)/p\) блокируется какой-нибудь потенциально доминирующий предиктор, стремящийся войти в каждое дерево. Если доминирование таких предикторов разрешить, то все деревья в итоге будут очень похожи друг на друга, а получаемые на их основе предсказания будут сильно коррелировать и снижение дисперсии будет не столь очевидным. Благодаря блокированию доминантов, другие предикторы получат свой шанс, и вариация деревьев возрастает.

Выбор малого значения m при построении случайного леса обычно будет полезным при наличии большого числа коррелирующих предикторов. Естественно, если случайный лес строится с использованием \(m = p\), то вся процедура сводится к простому бэггингу.

Применим методы бэггинга и случайного леса к прогнозированию данных по обилию водорослей в реках разного типа (см. три предыдущих раздела). Поскольку бэггинг - это просто частный случай метода случайного леса, то мы можем использовать одну и ту же функцию randomForest() пакета randomForest для R. Бэггинг выполняется, если задать параметр mtry = ncol(x):

load(file="algae.RData") # Загрузка таблицы algae - раздел 4.1
x <- as.data.frame(model.matrix(a1~ ., data = algae[, 1:12])[, -1])
library(randomForest)
set.seed(101)
randomForest(x, algae$a1, mtry = ncol(x))
## 
## Call:
##  randomForest(x = x, y = algae$a1, mtry = ncol(x)) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 15
## 
##           Mean of squared residuals: 275.4992
##                     % Var explained: 39.25

Как видно из полученных результатов, прогнозирование выполнялось по 500 деревьям, в которых было использовано только 40% исходных переменных. Оценить эффективность этой модели при перекрестной проверке можно с использованием функции train() из пакета caret:

set.seed(101)
(bag.a1 <- train(x, algae$a1,
                preProc = c('center', 'scale'),
                method = 'rf', trControl = trainControl(method = "cv"), 
                tuneGrid = expand.grid(.mtry = ncol(x))))
## Random Forest 
## 
## 200 samples
##  15 predictor
## 
## Pre-processing: centered (15), scaled (15) 
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 179, 181, 180, 180, 180, 180, ... 
## Resampling results:
## 
##   RMSE      Rsquared 
##   16.52067  0.4332375
## 
## Tuning parameter 'mtry' was held constant at a value of 15
##

Модель случайного леса можно построить этой же процедурой, задав последовательность значений mtry для оптимизации:

set.seed(101)
(ranfor.a1 <- train(x, algae$a1,
                   preProc = c('center', 'scale'),
                   method = 'rf', trControl = trainControl(method = "cv"), 
                   tuneGrid = expand.grid(.mtry = 2:10),
                   importance = TRUE))
## Random Forest 
## 
## 200 samples
##  15 predictor
## 
## Pre-processing: centered (15), scaled (15) 
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 179, 181, 180, 180, 180, 180, ... 
## Resampling results across tuning parameters:
## 
##   mtry  RMSE      Rsquared 
##    2    15.40795  0.4986732
##    3    15.53822  0.4907074
##    4    15.75865  0.4768690
##    5    15.85763  0.4706729
##    6    15.85864  0.4702870
##    7    16.08860  0.4572620
##    8    16.12184  0.4561278
##    9    16.30819  0.4454158
##   10    16.32886  0.4438528
## 
## RMSE was used to select the optimal model using  the smallest value.
## The final value used for the model was mtry = 2.

Заметим, что бутстреп дает хорошую возможность провести специальную процедуру перекрестной проверки, называемую тестом по “наблюдениям, не попавшим в сумку” (out-of-bag observations). Поскольку ключевая идея бэггинга состоит в многократном построении моделей по наблюдениям из бутстреп-выборок, то каждое конкретное дерево строится на основе примерно двух третей всех наблюдений. Остальная треть наблюдений не используется в обучении, но вполне может быть использована для независимого тестирования: ошибка на таких оставшихся данных (out–of–bag error) является состоятельной оценкой ошибки на контрольной выборке (Джеймс и др., 2016).

Основным преимуществом деревьев решений является привлекательная и легко интерпретируемая итоговая диаграмма вроде вроде тех, которые показаны в разделе 4.3. Хотя набор полученных в результате бэггинга деревьев гораздо сложнее интерпретировать, чем отдельно стоящее дерево, можно получить целых два обобщенных показателя важности каждого предиктора. Их графики легко построить при помощи функции varImpPlot()

varImpPlot(ranfor.a1$finalModel)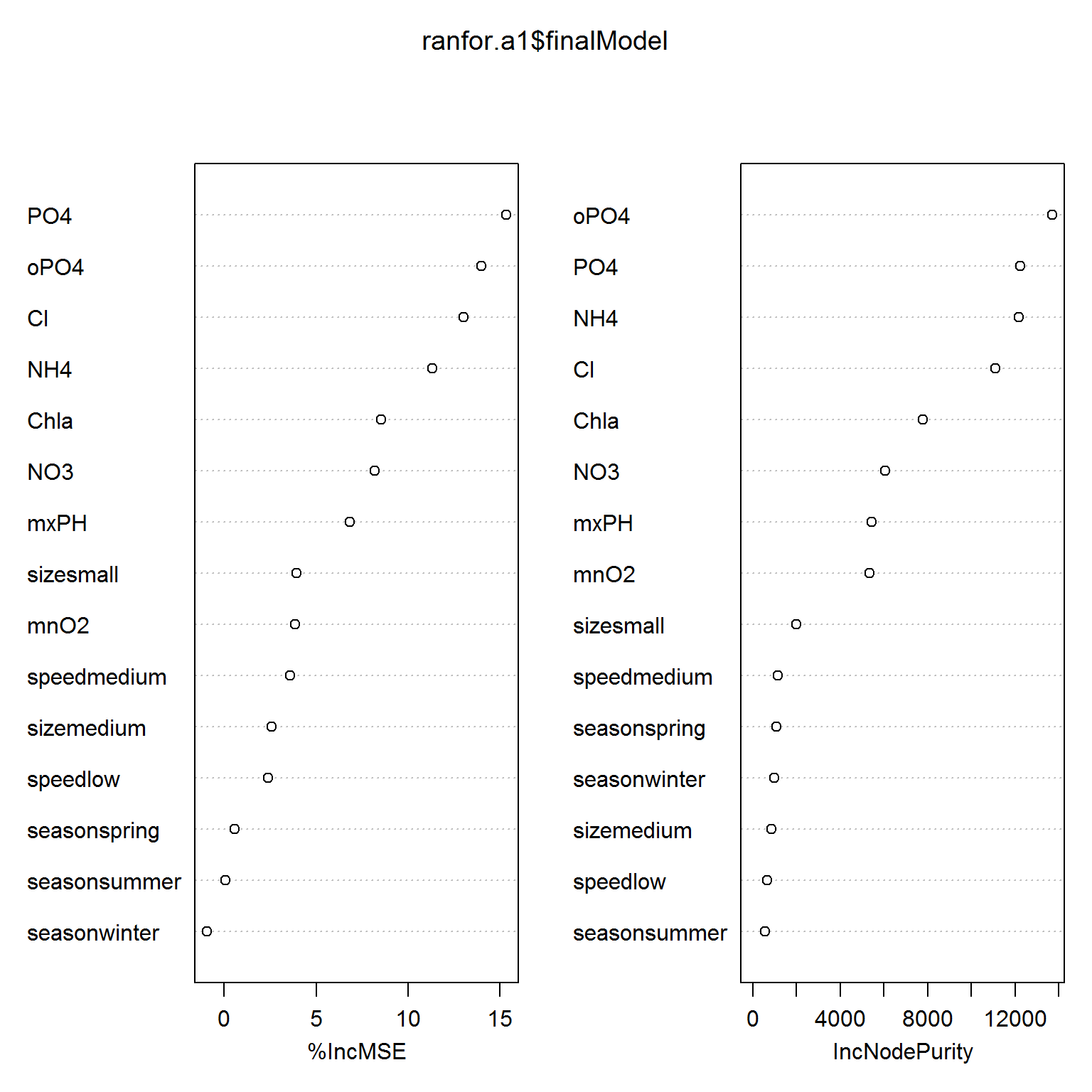
Показатели важности отдельных переменных для модели случайного леса

Рисунок 4.15: Показатели важности отдельных переменных для модели случайного леса

На рис. 4.15 приведены два показателя важности: %IncMSE основан на среднем снижении точности предсказания на оставшихся данных, а IncNodePurity - мера среднего увеличения “чистоты узла” дерева (node purity) в результате разбиения данных по соответствующей переменной. В случае деревьев регрессии чистота узла выражается через ошибку RSS.

Количество деревьев \(B\) не является критическим параметром при использовании бэггинга: очень большое значение \(B\) не приведет к переобучению. На практике обычно используется значение \(B\), достаточно большое для стабилизации ошибки: в частности, как следует из графика на рис. 4.16, величина \(B = 100\) уже обеспечивает хорошее качество предсказаний в нашем примере (по умолчанию, \(B = 500\)).

plot(ranfor.a1$finalModel, col = "blue", lwd = 2)
plot(bag.a1$finalModel, col = "green", lwd = 2, add = TRUE)
legend("topright", c("Bagging", "RandomForrest"),
       col = c("green","blue"), lwd = 2)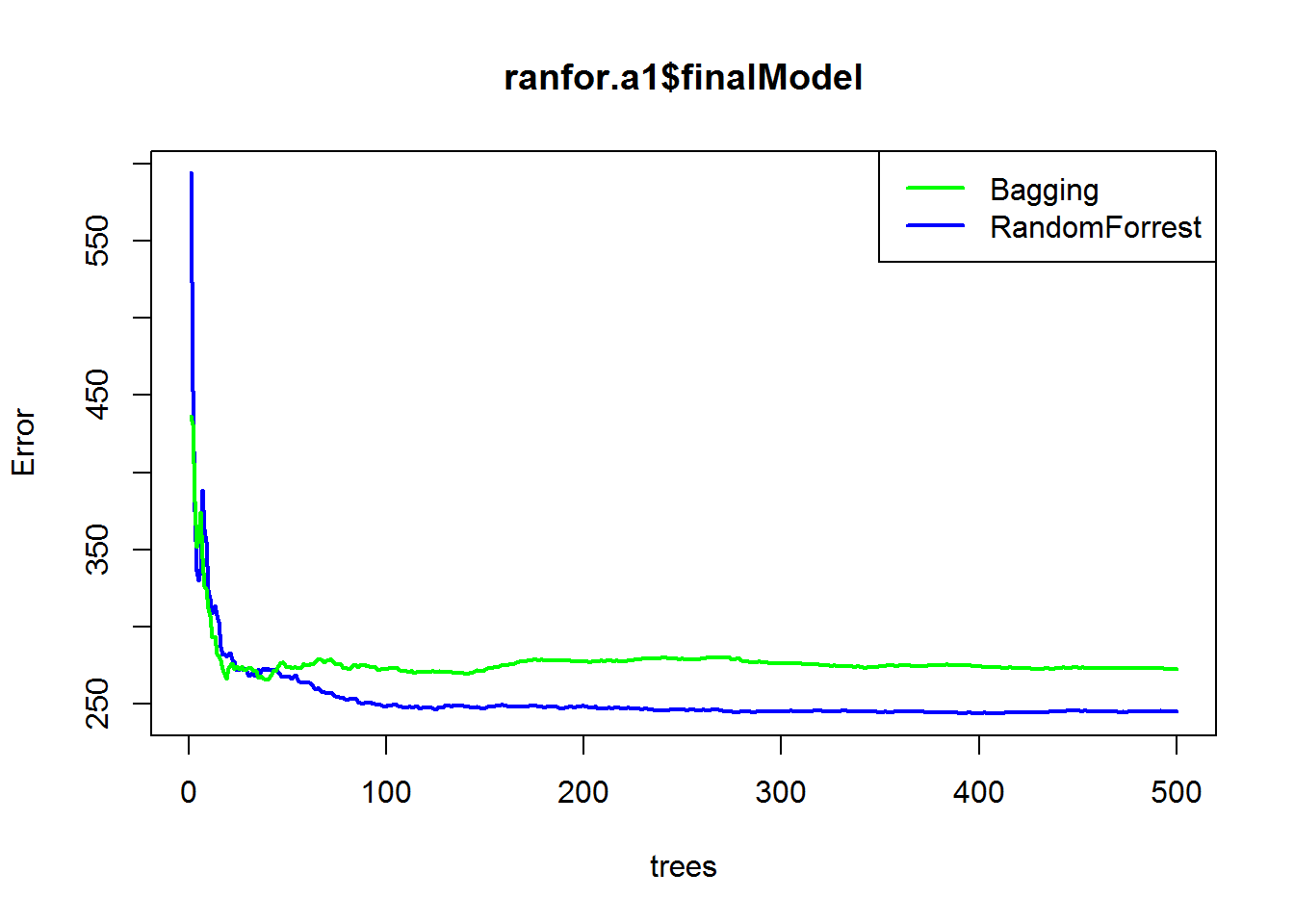
Зависимость ошибки на обучающей выборке от числа агрегируемых деревьев при бэггинге и использовании алгоритма "случайный лес"

Рисунок 4.16: Зависимость ошибки на обучающей выборке от числа агрегируемых деревьев при бэггинге и использовании алгоритма “случайный лес”

4.4.2 Бустинг

Другим методом улучшения предсказаний является бустинг (boosting), идея которого заключается в итеративном процессе последовательного построения частных моделей. Каждая новая модель обучается с использованием информации об ошибках, сделанных на предыдущем этапе, а результирующая функция представляет собой линейную комбинацию всего ансамбля моделей с учетом минимизации любой штрафной функции. Подобно бэггингу, бустинг является общим подходом, который можно применять ко многим статистическим методам регрессии и классификации. Здесь мы ограничимся обсуждением градиентного бустинга в контексте деревьев регрессии.

Бутстреп-выборки в ходе реализации бустинга не создаются, но вместо этого каждое дерево строится по набору данных \({X, r}\), который на каждом шаге модифицируется определенным образом. На первой итерации по значениям исходных предикторов строится дерево \(f^1(x)\) и находится вектор остатков \(r_1\). На последующем этапе новое регрессионное дерево \(f^2(x)\) строится уже не по обучающим данным \(X\), а по остаткам \(r_1\) предыдущей модели. Линейная комбинация прогноза по построенным деревьям дает нам новые остатки \(r_2 \leftarrow r_1 + \lambda f^2(x)\), и этот итерационный процесс повторяется \(B\) раз. Благодаря построению неглубоких деревьев по остаткам, прогноз отклика медленно улучшается в областях, где одиночное дерево работает не очень хорошо. Такие деревья могут быть довольно небольшими, лишь с несколькими конечными узлами. Параметр сжатия \(\lambda\) регулирует скорость этого процесса, позволяя создавать комбинации деревьев более сложной формы для “атаки” остатков. Итоговая модель бустинга представляет собой ансамбль \(\hat{f}(x) = \sum_{b_1}^B \lambda f^b(x)\).

В среде R для построения бустинг-моделей на основе деревьев решений можно использовать функцию gbm() из пакета gbm (Generalized Boosted Models). Процесс моделирования проходит под управлением трех гиперпараметров:

  1. Число деревьев \(В\) (формальный параметр n.tree). В отличие от бэггинга, бустинг может, хотя и медленно, приводить к переобучению при чрезмерно большом В.
  2. Параметр сжатия \(\lambda\) (shrinkage), который корректирует величину вклада каждого дополнительного дерева и контролирует скорость, с которой происходит обучение модели при реализации бустинга. Типичные значения \(\lambda\) варьируют от 0.01 до 0.001, и их оптимальный выбор зависит от решаемой проблемы. Для достижения хорошего качества предсказаний очень низкие значения \(\lambda\) требуют очень большого значения \(B\).
  3. Число внутренних узлов \(d\) (interaction.depth) в каждом дереве, которое контролирует сложность получаемого в результате бустинга ансамбля моделей. По своей сути, параметр \(d\) отражает глубину взаимодействий между предикторами в итоговой модели. Если эти взаимодействия не слишком выражены, то хорошо работает \(d = 1\), и тогда дополнительные деревья представляют собой просто “пни” (stump), т.е. содержат только один внутренний узел. В таком случае получаемый в результате бустинга ансамбль становится аддитивной моделью, поскольку каждый ее член представлен только одной переменной.

Тип решаемой задачи регулируется параметром distribution, который определяет оптимизируемую функцию:

  • для решения задач регрессии задается значение "gaussian" - квадратичный штраф, или "laplace" - штраф по абсолютной величине отклонения;
  • для задач бинарной классификации используют значение "bernoulli" - функция кросс-энтропии, или "adaboost" - экспоненциальный штраф.

Используем значение shrinkage = 0.001, установленное функцией gbm() по умолчанию. Функция summary() в отношение этого метода выводит список предикторов и соответствующие им значения показателя важности:

library(gbm)
set.seed(1)
xd <- cbind(a1 = algae$a1, x)
boost.a1 = gbm(a1 ~ ., data = xd, distribution = "gaussian",
n.trees = 1000, interaction.depth = 3)
summary(boost.a1, plotit = FALSE)
##                       var     rel.inf
## oPO4                 oPO4 28.46291329
## NH4                   NH4 24.40284599
## PO4                   PO4 20.25519899
## Cl                     Cl 14.62528341
## Chla                 Chla  4.78710908
## mxPH                 mxPH  2.55817883
## NO3                   NO3  2.06210934
## mnO2                 mnO2  1.63005364
## sizesmall       sizesmall  0.70955559
## speedmedium   speedmedium  0.20058490
## seasonwinter seasonwinter  0.13929129
## speedlow         speedlow  0.05886592
## seasonsummer seasonsummer  0.04095099
## sizemedium     sizemedium  0.03617319
## seasonspring seasonspring  0.03088555

Можно рассчитать среднюю ошибку модели на обучающей выборке, которая существенно меньше, чем при бэггинге:

pred = predict(boost.a1, x, n.trees = 1000)
mean((pred - algae$a1)^2)
## [1] 232.8693

Выполним оптимизацию параметров построения градиентного бустинга с использованием функции train(). Как скаано выше, таких параметров три:

Принимая во внимание, что параметры shrinkag и n.trees связаны обратно пропорциональной зависимостью, уменьшим число деревьев до 50, одновременно увеличив значение shrinkage по сравнению с применяемыми выше:

(gbmFit.a1 <- train(a1 ~ ., data = xd, 
                   method = "gbm", trControl = trainControl(method = "cv"), 
                   tuneGrid = expand.grid(shrinkage = c(0.1,0.05,0.02),
                                          interaction.depth = 2:5, n.trees = 50,
                                          n.minobsinnode = 10),
                   verbose = FALSE))
## Stochastic Gradient Boosting 
## 
## 200 samples
##  15 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 179, 180, 180, 179, 180, 180, ... 
## Resampling results across tuning parameters:
## 
##   shrinkage  interaction.depth  RMSE      Rsquared 
##   0.02       2                  16.19348  0.5037032
##   0.02       3                  16.14000  0.5060133
##   0.02       4                  16.13229  0.5094717
##   0.02       5                  16.03985  0.5161377
##   0.05       2                  15.54586  0.4918096
##   0.05       3                  15.42194  0.4969380
##   0.05       4                  15.23162  0.5082960
##   0.05       5                  15.23295  0.5092289
##   0.10       2                  15.40549  0.4984676
##   0.10       3                  15.43270  0.5014440
##   0.10       4                  15.62864  0.4921172
##   0.10       5                  15.45538  0.4997536
## 
## Tuning parameter 'n.trees' was held constant at a value of 50
## 
## Tuning parameter 'n.minobsinnode' was held constant at a value of 10
## RMSE was used to select the optimal model using  the smallest value.
## The final values used for the model were n.trees = 50, interaction.depth
##  = 4, shrinkage = 0.05 and n.minobsinnode = 10.

Бустинг деревьев регрессии может быть реализован также с использованием другого метода: с помощью функции bstTree() из пакета bst:

modelLookup("bstTree")
##     model parameter                 label forReg forClass probModel
## 1 bstTree     mstop # Boosting Iterations   TRUE     TRUE     FALSE
## 2 bstTree  maxdepth        Max Tree Depth   TRUE     TRUE     FALSE
## 3 bstTree        nu             Shrinkage   TRUE     TRUE     FALSE

Параметры, оптимизируемые методом bstTree, имеют несколько отличающиеся названия, но фактически эквивалентный содержательный смысл. Выполним их настройку с использованием параметров, заданных по умолчанию (рис. 4.17):

library(bst)                           
(boostFit.a1 <- train(a1 ~ ., data = xd, 
                     method = 'bstTree', trControl = trainControl(method = "cv"), 
                     preProc = c('center', 'scale')))
## Boosted Tree 
## 
## 200 samples
##  15 predictor
## 
## Pre-processing: centered (15), scaled (15) 
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 180, 179, 180, 181, 180, 180, ... 
## Resampling results across tuning parameters:
## 
##   maxdepth  mstop  RMSE      Rsquared 
##   1          50    15.66507  0.4838143
##   1         100    15.65839  0.4847449
##   1         150    15.62656  0.4844995
##   2          50    15.72647  0.4836585
##   2         100    16.23836  0.4576188
##   2         150    16.84847  0.4299882
##   3          50    16.20853  0.4625459
##   3         100    17.07712  0.4228308
##   3         150    17.51597  0.4033881
## 
## Tuning parameter 'nu' was held constant at a value of 0.1
## RMSE was used to select the optimal model using  the smallest value.
## The final values used for the model were mstop = 150, maxdepth = 1 and
##  nu = 0.1.
plot(boostFit.a1)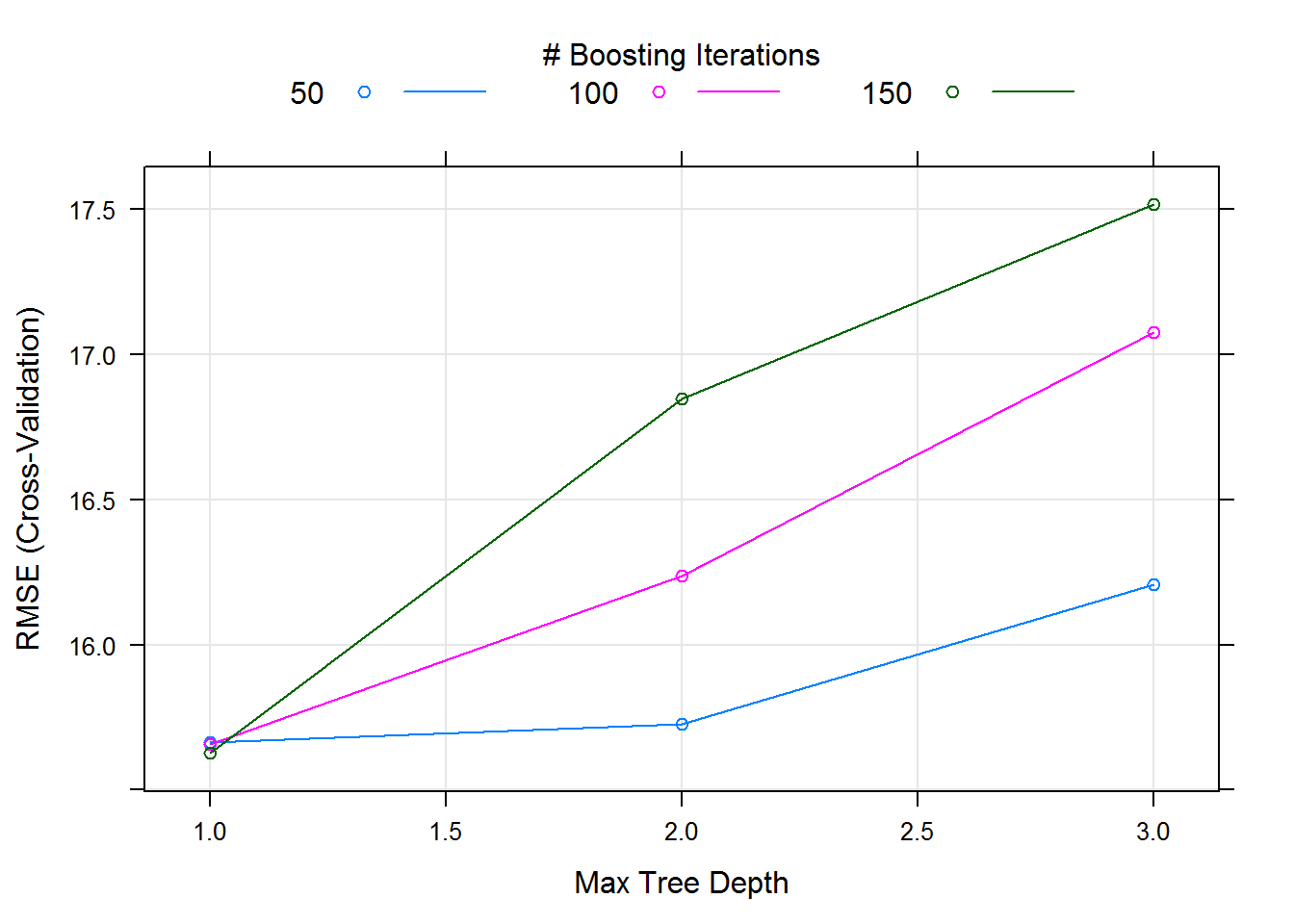
Зависимость ошибки от числа агрегируемых деревьев при бустинге (по результатам перекрестной проверки)

Рисунок 4.17: Зависимость ошибки от числа агрегируемых деревьев при бустинге (по результатам перекрестной проверки)

4.4.3 Тестирование моделей с использованием дополнительного набора данных

Используем для прогноза набор данных (Torgo, 2011) из 140 наблюдений, который мы уже применяли в предыдущем разделе. Данные, с восстановленными пропущенными значениями мы сохранили ранее в файле algae_test.RData (см раздел 4.1).

Выполним прогноз для набора предикторов тестовой выборки и оценим точность каждой модели по трем показателям: среднему абсолютному отклонению (MAE), корню из среднеквадратичного отклонения (RSME) и квадрату коэффициента детерминации Rsq = 1 - NSME, где NSME - относительная ошибка, равная отношению среднему квадрату отклонений от модельных значений и от общего среднего:

load(file = "algae_test.RData") # Загрузка таблиц Eval, Sols
y <- Sols$a1
EvalF <- as.data.frame(model.matrix(y ~ ., Eval)[, -1])
# Функция, выводящая вектор критериев
ModCrit <- function(pred, fact) {
    mae <- mean(abs(pred - fact))
    rmse <- sqrt(mean((pred - fact)^2))
    Rsq <- 1 - sum((fact - pred)^2)/sum((mean(fact) - fact)^2)
    c(MAE = mae, RSME = rmse, Rsq = Rsq) 
} 
Result <- rbind(
    bagging = ModCrit(predict(bag.a1, EvalF), Sols[, 1]),
    ranfor = ModCrit(predict(ranfor.a1, EvalF), Sols[, 1]),
    bst.gbm = ModCrit(predict(gbmFit.a1, EvalF), Sols[, 1]),
    bst.bst = ModCrit(predict(boostFit.a1, EvalF), Sols[, 1]))
Result
##               MAE     RSME       Rsq
## bagging  9.927347 14.44141 0.5031193
## ranfor   9.962148 14.10063 0.5262930
## bst.gbm 10.351657 14.79918 0.4781952
## bst.bst 10.108705 14.67850 0.4866704