7.2 Наивный байесовский классификатор

В основе байесовской классификации лежит гипотеза максимальной вероятности, т.е. объект \(d\) считается принадлежащим классу \(c_j\) (\(c_j \in C\)), если при достигается наибольшая апостериорная вероятность: \(\underset{c}{\max} P(c_j | d)\). По формуле Байеса, \[ P(c_j | d) = \frac{P(c_j) P(d | C_j)}{P(d)} \approx P(c_j) P(d | c_j), \]

где \(P(d|c_j)\) - вероятность встретить объект \(d\) среди объектов класса \(c_j\); \(P(c_j)\) и \(P(d)\) - априорные вероятности класса \(c_j\) и объекта \(d\) (последняя, не влияет на выбор класса и может быть опущена).

Если сделать “наивное” предположение, что все признаки, описывающие классифицируемые объекты, совершенно равноправны между собой и не связаны друг c другом, то \(P(d|c_j)\) можно вычислить как произведение вероятностей встретить признак \(x_i\) (\(x_i \in \mathbf{X}\)) среди объектов класса \(c_j:\)

\[ P(d | c_j) = \prod_{i=1}^{|\mathbf{X}|} P(x_i | c_j),\]

где \(P(x_i|c_j)\) - вероятностная оценка вклада признака \(x_i\) в то, что \(d \in c_j\).

На практике при умножении очень малых условных вероятностей может наблюдаться потеря значащих разрядов, в связи с чем вместо самих оценок вероятностей \(P(x_i|c_j)\) применяют логарифмы этих вероятностей. Поскольку логарифм - монотонно возрастающая функция, то класс \(c_j\) с наибольшим значением логарифма вероятности останется наиболее вероятным. Тогда решающее правило наивного байесовского классификатора (Naive Bayes Classifier) принимает следующий окончательный вид:

\[c^* = \arg_{c_j \in \mathbf{C}} \max[\log P(c_j) + \sum_{i=1}^\mathbf{X} P(x_i | c_j)].\]

Остается только позаботиться, чтобы значения логарифмируемых вероятностей были не слишком близки к 0 (чтобы этого не случилось, можно применить лапласовское сглаживание).

В среде R расчеты выполняются обычно с использованием функций NaiveBayes() из пакета klaR или naiveBayes() из пакета e1071. Рассмотрим их использование на примере классификации цветков ириса:

library(klaR)
naive_iris <- NaiveBayes(iris$Species ~ ., data = iris)
naive_iris$tables$Petal.Width

##             [,1]      [,2]
## setosa     0.246 0.1053856
## versicolor 1.326 0.1977527
## virginica  2.026 0.2746501

Для каждой метрической независимой переменной были выведены средние значения Petal.Width (первый столбец) и их стандартные отклонения (второй столбец) для каждого выделенного класса. Можно установить, что ширина лепестка у виргинского ириса существенно выше, чем у остальных двух видов:

Для визуальной сравнительной оценки связи измеренных переменных с метками классов удобно рассмотреть ядерные функции плотности условной вероятности (рис. 7.6):

plot(naive_iris, lwd = 2)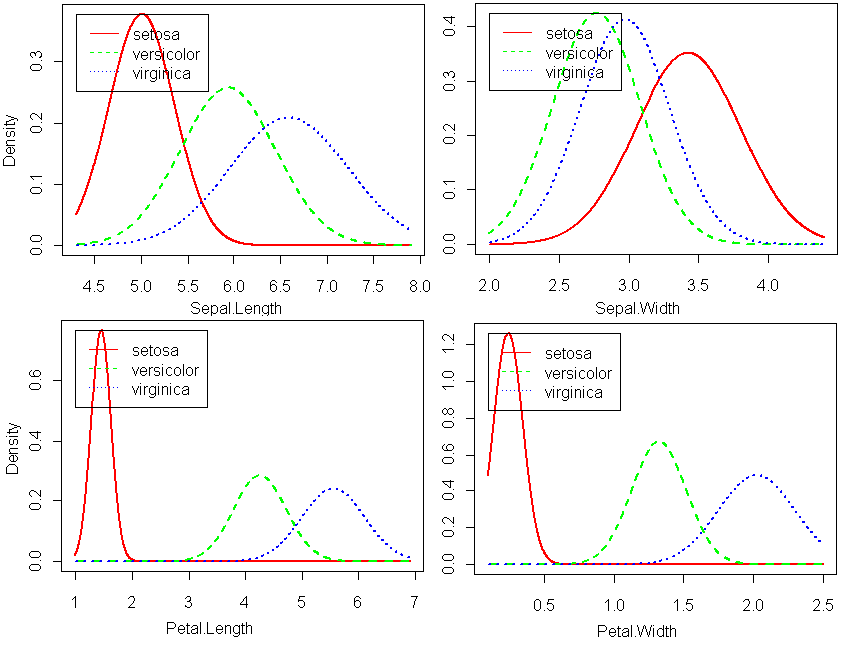

Рисунок 7.6: Кривые ядерной плотности условной вероятности для предикторов из набора данных по ирисам

Выполним прогноз вида ирисов для объектов из обучающей выборки:

pred <- predict(naive_iris, iris[, -5])$class
(table(Факт = iris$Species, Прогноз = pred))

##             Прогноз
## Факт         setosa versicolor virginica
##   setosa         50          0         0
##   versicolor      0         47         3
##   virginica       0          3        47

Acc <- mean(pred == iris$Species)
paste("Точность=", round(100*Acc, 2), "%", sep = "")

## [1] "Точность=96%"

Осуществим 10-кратную перекрестную проверку построенной модели, чтобы установить качество ее предсказаний на контрольных примерах. Одновременно уточним значения некоторых гиперпараметров процедуры вычисления вероятностей по частотам: надо ли использовать ядерное сглаживание (usekernel = TRUE) или можно предположить нормальное распределение, а также следует ли проводить коррекцию вероятностей по Лапласу fL. Для этого снова воспользуемся функцией train() из пакета caret:

library(caret)
#  Определим условия перекрестной проверки: 
train_control <- trainControl(method = 'cv', number = 10)
Test <- train(Species ~ ., data = iris, trControl = train_control, method = "nb")
print(Test)

## Naive Bayes 
## 
## 150 samples
##   4 predictor
##   3 classes: 'setosa', 'versicolor', 'virginica' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 135, 135, 135, 135, 135, 135, ... 
## Resampling results across tuning parameters:
## 
##   usekernel  Accuracy   Kappa
##   FALSE      0.9533333  0.93 
##    TRUE      0.9600000  0.94 
## 
## Tuning parameter 'fL' was held constant at a value of 0
## Tuning
##  parameter 'adjust' was held constant at a value of 1
## Accuracy was used to select the optimal model using  the largest value.
## The final values used for the model were fL = 0, usekernel = TRUE
##  and adjust = 1.

Acc <- mean(predict(Test$finalModel, iris[, -5])$class == iris$Species)
paste("Точность=", round(100*Acc, 2), "%", sep="")

## [1] "Точность=96%"

Более качественной модели в результате перекрестной проверки построить не удалось, но точность классификатора на обучающей и контрольной выборках осталась стабильно высокой.