2.2 Использование алгоритмов ресэмплинга для тестирования моделей и оптимизации их параметров
Фундаментальным для статистики является рассуждение о соотношении свойств случайных выборок и генеральной совокупности, из которых они были извлечены. Любой эксперимент в принципе ограничен некоторым (чаще всего, небольшим) множеством наблюдений, причем никакие сверхинтеллектуальные методы обработки не являются панацеей от влияния неучтенных факторов или систематических погрешностей. Один из возможных путей надежного оценивания свойств данных заключается в использовании компьютерно-интенсивных (computer-intensive) технологий, объединенных общим термином “численный ресэмплинг” (англ. resampling) или, как их иногда называют в русскоязычной литературе, “методов генерации повторных выборок” (Эфрон, 1988; Edgington, 1995; Davison, Hinkley, 2006). Ключевая особенность этой технологии заключается в том, что повторные выборки при классическом сценарии извлекаются из генеральной совокупности, а псевдоповторные выборки при выполнении ресэмплинга - из самой эмпирической выборки (хорошо известна фраза “The population is to the sample as the sample is to the bootstrap samples” из работы Fox, 2002).
Ресэмплинг объединяет четыре разных подхода к обработке данных, отличающихся по алгоритму, но близких по сути: перекрестная проверка (cross-validation, CV), бутстреп (bootstrap), рандомизация, или перестановочный тест (permutation), и метод “складного ножа” (jackknife). Ниже рассматриваются два из них: перекрестная проверка для оптимизации параметров модели и бутстреп для оценивания доверительных интервалов критериев эффективности моделей.
Минимизация ошибок на обучающем множестве, которое не бывает ни идеальным, ни бесконечно большим, неизбежно приводит к моделям, смещенным относительно истинной функции процесса, порождающего наблюдаемые данные. Преодолеть это смещение можно только с использованием “принципа внешнего дополнения”, т.е. блоков “свежих” данных, не участвовавших в построении модели.
При отсутствии дополнительных блоков данных, специально предназначенных для тестирования, вполне естественно выглядит идея провести случайное разбиение исходной выборки на обучающее (train sample) и проверочное (test sample) подмножества, после чего оценить параметры модели только на обучающей выборке, тогда как оценку погрешности прогноза отклика \(\hat{y}_i\) осуществить для значений из проверочной совокупности. Если подобные шаги выполняются многократно и каждое из наблюдений используется поочередно то для обучения, то для контроля, то такая процедура эмпирического оценивания моделей, построенных по прецедентам, называется перекрестной проверкой, или “кросс-проверкой”.
Стандартной считается методика \(r \times k\)-кратной кросс-проверки (\(r \times k\)-fold cross-validation), когда исходная выборка случайным образом \(r\) раз разбивается на \(k\) блоков (folds) равной (или почти равной) длины. При реализации каждой повторности \(r\) (replication) один из блоков по очереди становится проверочной совокупностью, а все остальные блоки - одной большой обучающей выборкой (рис. 2.5):
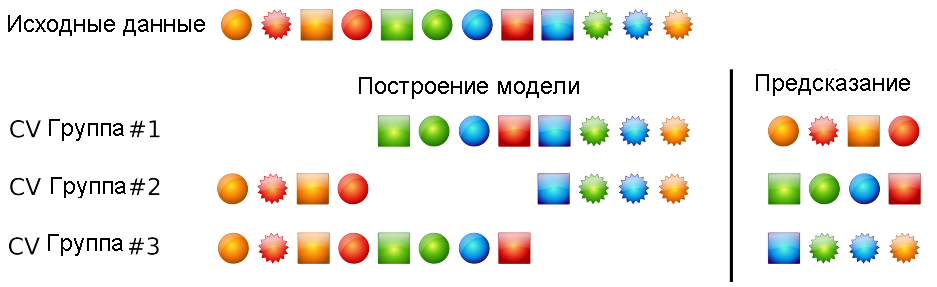
Рисунок 2.5: Пример 1x3-кратной кросс-проверки
При этом генерируется \(r \times k\) значений отклика \(\hat{y}\), и ошибкой перекрестной проверки при использовании модели \(М\) на исходной выборке \(X^n\) называется средняя по всем \(k\) разбиениям величина ошибки на контрольных подмножествах: \[S_{CV} = \sqrt{\frac{1}{r \times n} \sum_{i=1}^{r \times n} (y_i - \hat{y}_i)^2}.\]
Выполнить разбиение исходной выборки y на k блоков можно с использованием различных функций R, например, из пакета caret:
createDataPartition(y, p = 0.5)
createFolds(y, k = 10)
createMultiFolds(y, k = 10, times = r)Частным случаем является “скользящий контроль”, или перекрестная проверка с последовательным исключением одного наблюдения (leave-one-out CV, LOOCV), т.е. \(k = n\). При этом строится \(n\) моделей по \((n – 1)\) выборочным значениям, а исключенное наблюдение каждый раз используется для расчета ошибки прогноза. В. Н. Вапник (1984) теоретически обосновал применение скользящего контроля и показал, что если исходные выборки независимы, то средняя ошибка перекрестной проверки даёт несмещённую оценку ошибки модели. Это выгодно отличает её от средней ошибки на обучающей выборке, которая при переусложнении модели может оказаться оптимистично заниженной.
В разделе 2.1 мы рассматривали пример выбора оптимального числа параметров полиномиальной регрессии с использованием информационных критериев. Попробуем достичь той же цели, выполнив перекрестную проверку моделей в режиме “leave-one-out” с использованием самостоятельно оформленной функции:
# Функция скользящего контроля для модели y~poly(x, degree):
crossvalidate <- function(x, y, degree) {
preds <- numeric(length(x))
for (i in 1:length(x)) {
x.in <- x[-i]; x.out <- x[i]
y.in <- y[-i]; y.out <- x[i]
m <- lm(y.in ~ poly(x.in, degree = degree) )
new <- data.frame(x.in = seq(-3, 3, by = 0.1))
preds[i] <- predict(m, newdata = data.frame(x.in = x.out))
}
# Тестовая статистика - сумма квадратов отклонений:
return(sum((y - preds)^2))
}
# Заполнение таблицы результатами кросс-проверки
# и сохранение квадрата ошибки в таблице "a"
a <- data.frame(cross = numeric(max.poly))
for (i in 1:max.poly) {
a[i, 1] <- crossvalidate(x, y, degree = i)
}
# График суммы квадратов ошибки при кросс-проверке:
qplot(1:max.poly, cross, data = a, geom = c("line")) +
xlab("Степень полинома ") + ylab("Квадратичная ошибка")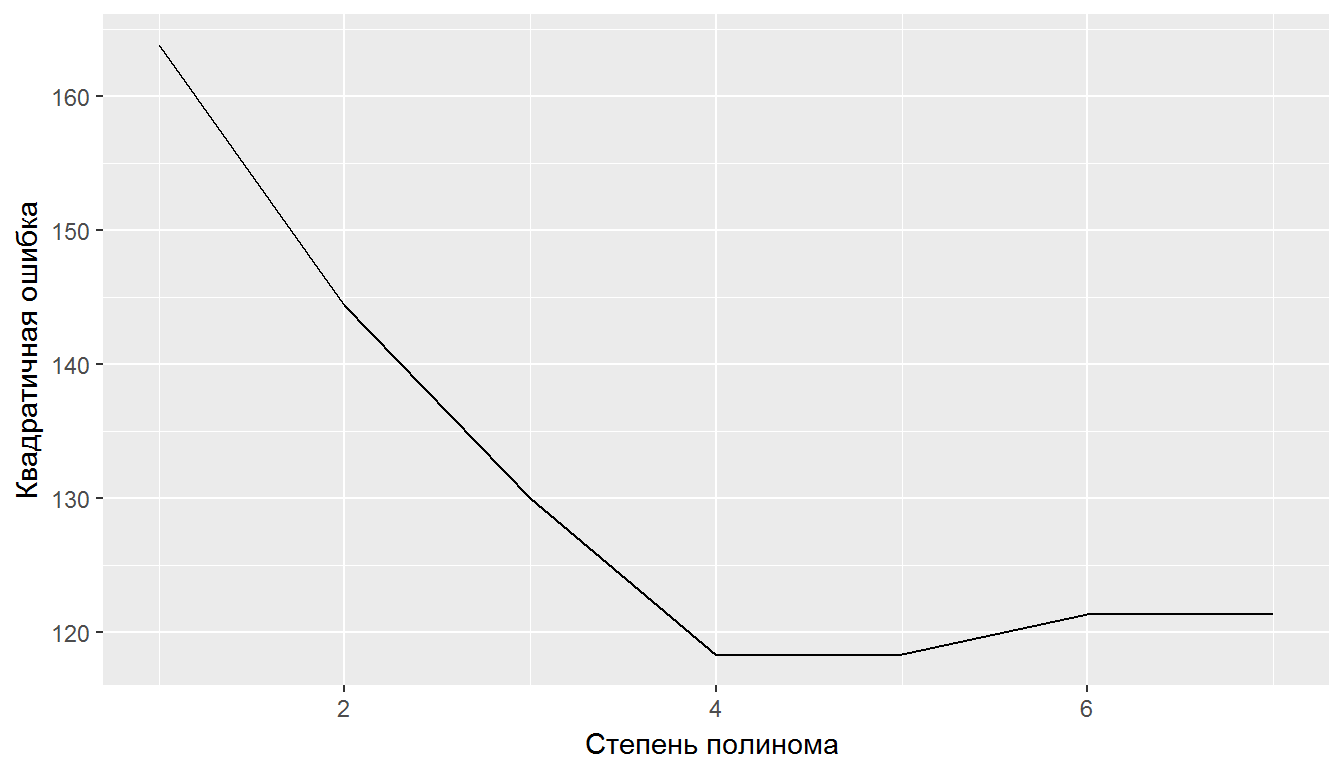
Рисунок 2.6: Поиск степени функции полиномиальной регрессии с использованием перекрестной проверки
Как видно из графика на рис. 2.6, по мере усложнения модели от линейной регрессии с одним предиктором до полинома 7-й степени ошибка предсказаний на проверочном множестве (test error) сначала снижается, а затем после достижения некоторого минимума начинает возрастать. Такая \(U\)-образная форма поведения ошибки является универсальной и справедлива практически для любых алгоритмов и методов создания предсказательных моделей. Повторный рост ошибки на проверочных данных является сигналом о том, что модель стала переобученной. Результаты, представленные на рис. 2.4 и 2.6, говорят о том, что в нашем конкретном случае оба метода одинаково выбирают в качестве наилучшей модели полином 4-й степени.
Проверим, является ли статистически значимым превышение качества полиномиальной модели над моделью с одним предиктором:
(M_poly <- glm(y ~ poly(x, 4)))##
## Call: glm(formula = y ~ poly(x, 4))
##
## Coefficients:
## (Intercept) poly(x, 4)1 poly(x, 4)2 poly(x, 4)3 poly(x, 4)4
## 4.360 -16.750 4.751 3.946 -3.371
##
## Degrees of Freedom: 127 Total (i.e. Null); 123 Residual
## Null Deviance: 439.3
## Residual Deviance: 109.2 AIC: 354.9anova(M_glm, M_poly, test = "Chisq")## Analysis of Deviance Table
##
## Model 1: y ~ x
## Model 2: y ~ poly(x, 4)
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 126 158.71
## 2 123 109.21 3 49.501 4.743e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Имеет место статистически значимое снижение ошибки модели.
В среде R перекрестную проверку модели можно выполнить не только на основе самостоятельно оформленных процедур, но и с использованием нескольких общедоступных функций из известных пакетов:
CVlm(df, form.lm, m = 3)из пакетаDAAG, гдеdf- исходная таблица с данными,form.lm- формула линейной модели,m- число блоков (сюда подставляется значение \(k\));cv.glm(df, glmfit, K = n)из пакетаboot, гдеdf- исходная таблица с данными,glmfit- объект обобщенной линейной модели типаglm,K- число блоков (т.е. по умолчанию выполняется скользящий контроль);cvLm(lmfit, folds = cvFolds(n, K, R), cost)из пакетаcvTools, гдеlmfit- объект обобщенной линейной моделиlm,K- число блоков,R- число повторностей,cost- наименование одного из пяти разновидностей используемых критериев качества;train(form, df, method, trainControl, ...)из пакета caret, гдеdf- исходная таблица с данными,form,method- формула и метод построения модели,trainControl- объект, в котором прописываются все необходимые параметры перекрестной проверки.
Бутстреп-процедура состоит в том, чтобы случайным образом многократно извлекать повторные выборки из эмпирического распределения. Конкретно, если мы имеем исходную выборку из \(n\) членов \(x_1, x_2, \dots, x_{n - 1}, x_n\), то с помощью датчика случайных чисел, равномерно распределенных на интервале \([1, n]\), можем вытянуть из нее произвольный элемент \(x_k\), который снова вернем в исходную выборку для возможного повторного извлечения. Такая процедура повторяется \(n\) раз и образуется бутстреп-выборка, в которой одни элементы могут повторяться два или более раз, тогда как другие элементы - отсутствовать. Например, при \(n = 6\) одна из таких бутстреп-комбинаций имеет вид \(x_4, x_2, x_2, x_1, x_4, x_5\).
В R бутстреп легко реализуется с помощью функции sample(..., replace = TRUE), генерирующей любые случайные выборки с “возвращением”. Вероятность того, что конкретное наблюдение не войдет в бутстреп-выборку размера \(n\), равна \((1 - 1/n)n\) и стремится к \(1/e = 0.368\) при \(n \rightarrow \infty\):
Nboot = 1000; n = 100
mean(replicate(Nboot, length(unique(sample(n, replace = TRUE)))))## [1] 63.432Таким способом можно сформировать любое, сколь угодно большое число бутстреп-выборок (обычно 500-1000), каждая из которых содержит около 2/3 уникальных значений эмпирической совокупности.
В результате легкой модификации частотного распределения реализаций исходных данных можно ожидать, что каждая следующая генерируемая псевдовыборка будет обладать значением оцениваемого параметра, немного отличающемся от вычисленного для первоначальной совокупности. На основе разброса значений анализируемого показателя, полученного в ходе такого процесса имитации, можно построить, например, доверительные интервалы оцениваемого параметра.
В предыдущем разделе мы рассматривали использование информационных критериев для выбора оптимальной степени полинома. Осуществим оценку квантильных интервалов байесовского критерия BIC для каждой из модели-претендента:
set.seed(123)
Nboot = 1000
BootMat <- sapply(1:max.poly, function(k)
replicate(Nboot, {
ind <- sample(n, replace=T)
BIC(glm(y[ind]~poly(x[ind],k)))
} )
)
apply(BootMat, 2, mean)## [1] 311.5186 316.0324 305.9600 303.1222 304.7347 308.1959 305.3907Искомые интервалы покажем на графике (рис. 2.7), подключив функцию stat_summary() из пакета ggplot2:
library(reshape) # для функции melt()
BootMat.df <- data.frame(melt(BootMat))
ggplot(data = BootMat.df, aes(X2, value)) +
geom_jitter(position = position_jitter(width = 0.1),
alpha = 0.2) +
# Добавляем средние значения в виде точек красного цвета:
stat_summary(fun.y = mean, geom = "point", color = "red",
size = 5) +
# Добавляем отрезки, символизирующие 0.25 и 0.75 квантили:
stat_summary(fun.y = mean,
fun.ymin = function(x){quantile(x, p = 0.25)},
fun.ymax = function(x){quantile(x, p = 0.75)},
geom = "errorbar", color = "magenta", width = 0.5,
size =1.5) +
xlab("Степень полинома") +
ylab("Информационный критерий Байеса")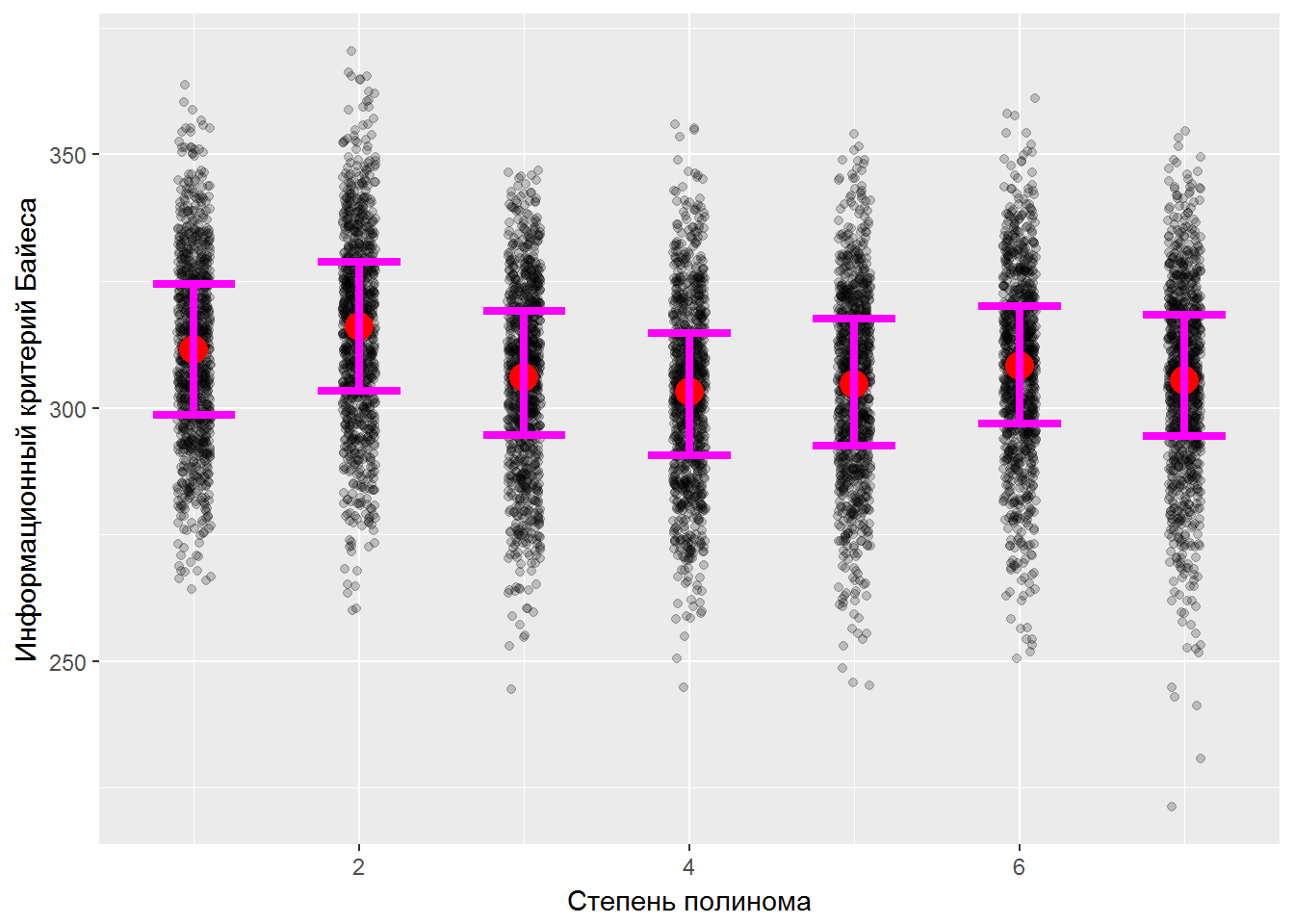
Рисунок 2.7: Доверительные интервалы байесовского информационного критерия для разных степеней полинома
Для оценки 95%-х доверительных интервалов методом процентилей достаточно установить значения p = c(0.025, 0.975) (мы это не сделали исключительно из эстетических соображений). Из результатов бутстрепа можно сделать содержательные выводы, например: если доверительные интервалы смежных степеней полинома будут пересекаться, то уменьшение BIC статистически незначимо и вполне можно ограничиться более простой моделью. Подробнее о различных возможностях ресэмплинга см. книгу В. Шитикова и Г. Розенберга (2014).