Классификация, регрессия и другие алгоритмы Data Mining с использованием R

3.4 Заполнение пропущенных значений в данных

К сожалению, на практике в ходе сбора данных далеко не всегда удается полностью укомплектовать исходные таблицы. Пропуски отдельных значений являются повсеместным явлением и поэтому, прежде чем начать применять статистические методы, обрабатываемые данные следует привести к “каноническому” виду. Для этого необходимо либо удалить фрагменты объектов с недостающими элементами, либо заменить имеющиеся пропуски на некоторые разумные значения.

Проблема “борьбы с пропусками” столь же сложна, как и сама статистика, поскольку в этой области существует впечатляющее множество подходов. В русскоязычных книгах по использованию R (Кабаков, 2014; Мастицкий, Шитиков, 2015) бегло представлены только некоторые функции пакета mice, который, несмотря на свою “продвинутость”, мало удобен для практической работы с данными умеренного и большого объема. Хорошей альтернативой являются методы "knnImpute", "bagImpute" и "medianImpute" функции preProcess() из пакета caret, которую мы рассмотрели в разделе 3.3 как инструмент для трансформации данных.

Используем в качестве примера для дальнейших упражнений таблицу algae, включенную в пакет DMwR и содержащую данные гидробиологических исследований обилия водорослей в различных реках. Каждое из 200 наблюдений содержит информацию о 18 переменных, в том числе:

три номинальных переменных, описывающих размеры size = c("large", "medium", "small") и скорость течения реки speed = c("high", "low", "medium"), а также время года season = c("autumn", "spring", "summer", "winter"), сопряженное с моментом взятия проб;
8 переменных, составляющих комплекс наблюдаемых гидрохимических показателей: максимальное значение рН mxPH (1), минимальное содержание кислорода mnO2 (2), хлориды Cl (10), нитраты NO3 (2), ионы аммония NH4 (2), орто-фосфаты oPO4 (2), общий минеральный фосфор PO4 (2) и количество хлорофилла а Chla (12) (в скобках приведено число пропущенных значений);
средняя численность каждой из 7 групп водорослей a1 - a7 (видовой состав не идентифицировался).

Читатель может самостоятельно воспользоваться функциями описательной статистики summary() или describe() из пакета Hmisc, а мы постараемся поддержать добрую традицию и привести парочку примеров диаграмм, построенных с использованием пакета ggplot2 (рис. 3.4):

library(DMwR)
library(ggplot2)
# summary(algae) # вывод не приводится
ggplot(data = algae[!is.na(algae$mnO2), ], aes(speed , mnO2)) + 
       geom_violin(aes(fill = speed), trim = FALSE, 
       alpha = 0.3) + 
       geom_boxplot(aes(fill = speed), width = 0.2,
       outlier.colour = NA) + 
       theme(legend.position = "NA")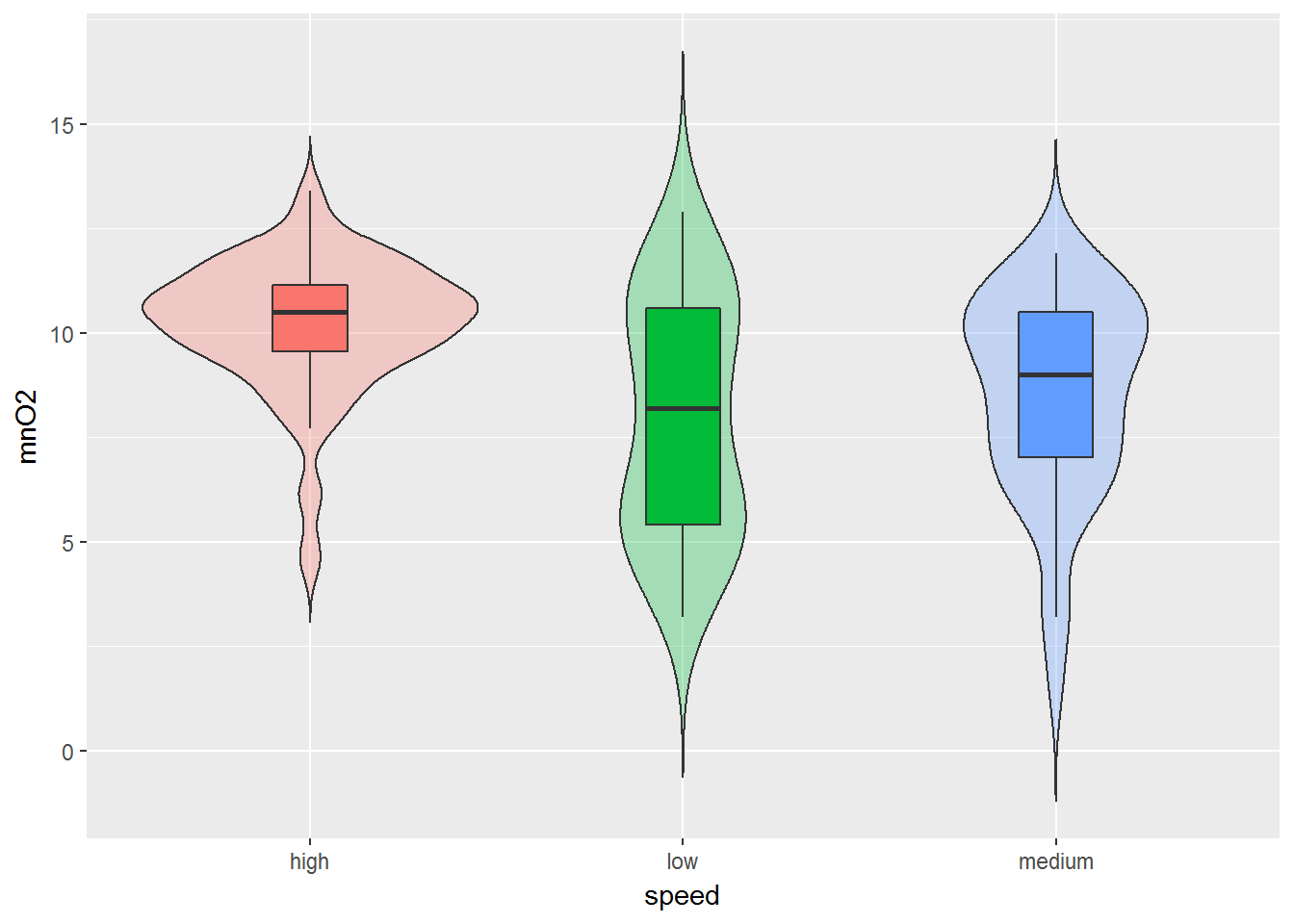

Рисунок 3.4: Распределения значений содержания кислорода в воде рек с разной скоростью течения

На рис. 3.4 мы получили так называемую “скрипичную диаграмму” (violin plot), которая объединяет в себе идеи диаграмм размахов и кривых распределения вероятности. Суть достаточно проста: продольные края “ящиков с усами” (для сравнения приведены тоже) замещаются кривыми плотности вероятности. В итоге, например, легко можно выяснить не только тот факт, что в потоках с быстрым течением (high) содержание кислорода выше, но и ознакомиться с характером распределения соответствующих значений.

Другой пример - категоризованные графики, удобные для визуализации данных, разбитых на отдельные подмножества (категории), каждое из которых отображается в отдельной диаграмме подходящего типа. Такие диаграммы, или “панели” (от англ. panels, facets или multiples), определенным образом упорядочиваются и размещаются на одной странице. Из графиков, представленных на рис. 3.5, легко увидеть, что численность водорослей группы а1 падает с увеличением концентрации фосфатов.

qplot(PO4, a1, data = algae[!is.na(algae$PO4), ]) +
      facet_grid(facets = ~ season) +
      geom_smooth(color = "red", se = FALSE)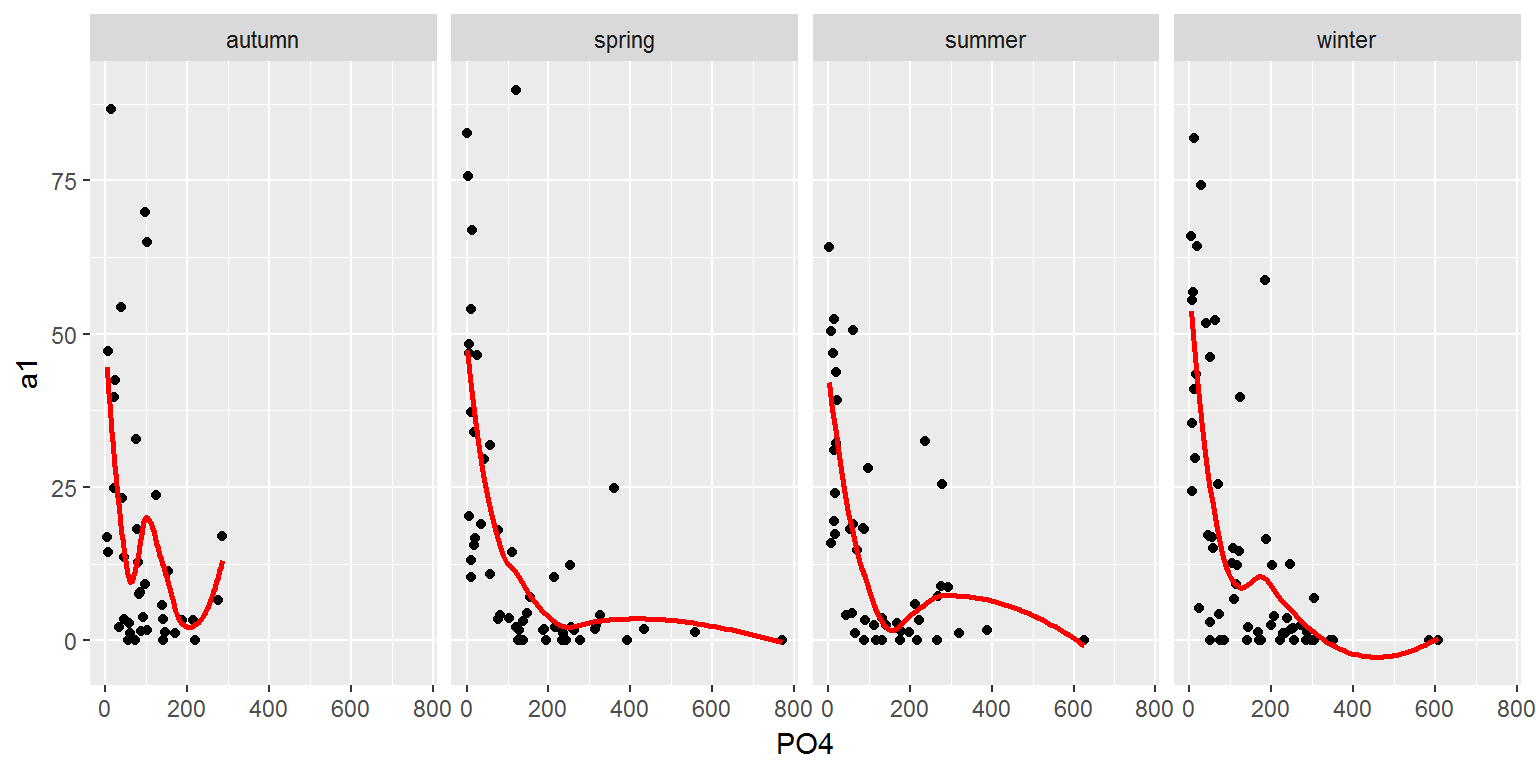

Рисунок 3.5: Графики изменения обилия водорослей в зависимости от содержания минерального фосфора в разное время года

Однако в контексте темы этого раздела важно обратить внимание на то, что мы все время старались блокировать появление пропущенных значений: algae[!is.na(algae$PO4), ]. Если в обрабатываемой таблице обнаружены недостающие данные, то в общих чертах можно избрать одну из следующих возможных стратегий:

удалить строки с неопределенностями;
заполнить неизвестные значения выборочными статистиками соответствующей переменной (среднее, медиана и т.д.), полагая, что взаимосвязь между переменными в имеющемся наборе данных отсутствует (это соответствует известному “наивному” подходу);
заполнить неизвестные значения с учетом корреляции между переменными или меры близости между наблюдениями; постараться обходить эту неприятную ситуацию, используя, например, формальный параметр na.rm некоторых функций.

Последняя альтернатива является наиболее ограничивающей, поскольку она далеко не во всех случаях позволяет осуществить необходимый анализ. В свою очередь, удаление целых строк данных слишком радикально и может привести к серьезным потерям важной информации:

# Число строк с пропущенными значениями:
nrow(algae[!complete.cases(algae),])

## [1] 16

# Их удаление:
algae <- na.omit(algae)

Можно удалить не все строки, а только те, в которых число пропущенных значений превышает, например, 20% от общего числа переменных, для чего существует специальная функция из пакета DMwR:

data(algae)
manyNAs(algae, 0.2)

## [1]  62 199

algae <- algae[-manyNAs(algae, 0.2), ]

В результате мы удалили только две строки (62-ю и 199-ю), где число пропущенных значений больше одного. Обратите внимание, что выполняя команду data(algae), мы каждый раз обновляем в памяти содержимое этого набора данных.

Если мы готовы принять гипотезу о том, что зависимостей между переменными нет, то простым и часто весьма эффективным способом заполнения пропусков является использование средних значений. В том случае, если есть сомнения в нормальности распределения данных, предпочтительнее использовать медиану. Покажем, как это можно сделать с использованием функции preProcess() из пакета caret:

data(algae)
ind <- apply(algae, 1, function(x) sum(is.na(x))) > 0
algae[ind, 4:11]

##     mxPH mnO2    Cl   NO3 NH4    oPO4     PO4  Chla
## 28  6.80 11.1 9.000 0.630  20   4.000      NA  2.70
## 38  8.00   NA 1.450 0.810  10   2.500   3.000  0.30
## 48    NA 12.6 9.000 0.230  10   5.000   6.000  1.10
## 55  6.60 10.8    NA 3.245  10   1.000   6.500    NA
## 56  5.60 11.8    NA 2.220   5   1.000   1.000    NA
## 57  5.70 10.8    NA 2.550  10   1.000   4.000    NA
## 58  6.60  9.5    NA 1.320  20   1.000   6.000    NA
## 59  6.60 10.8    NA 2.640  10   2.000  11.000    NA
## 60  6.60 11.3    NA 4.170  10   1.000   6.000    NA
## 61  6.50 10.4    NA 5.970  10   2.000  14.000    NA
## 62  6.40   NA    NA    NA  NA      NA  14.000    NA
## 63  7.83 11.7 4.083 1.328  18   3.333   6.667    NA
## 116 9.70 10.8 0.222 0.406  10  22.444  10.111    NA
## 161 9.00  5.8    NA 0.900 142 102.000 186.000 68.05
## 184 8.00 10.9 9.055 0.825  40  21.083  56.091    NA
## 199 8.00  7.6    NA    NA  NA      NA      NA    NA

library(caret)
pPmI <- preProcess(algae[, 4:11], method = 'medianImpute')
algae[, 4:11] <- predict(pPmI, algae[, 4:11])
(Imp.Med <- algae[ind, 4:11])

##     mxPH mnO2     Cl   NO3      NH4    oPO4      PO4   Chla
## 28  6.80 11.1  9.000 0.630  20.0000   4.000 103.2855  2.700
## 38  8.00  9.8  1.450 0.810  10.0000   2.500   3.0000  0.300
## 48  8.06 12.6  9.000 0.230  10.0000   5.000   6.0000  1.100
## 55  6.60 10.8 32.730 3.245  10.0000   1.000   6.5000  5.475
## 56  5.60 11.8 32.730 2.220   5.0000   1.000   1.0000  5.475
## 57  5.70 10.8 32.730 2.550  10.0000   1.000   4.0000  5.475
## 58  6.60  9.5 32.730 1.320  20.0000   1.000   6.0000  5.475
## 59  6.60 10.8 32.730 2.640  10.0000   2.000  11.0000  5.475
## 60  6.60 11.3 32.730 4.170  10.0000   1.000   6.0000  5.475
## 61  6.50 10.4 32.730 5.970  10.0000   2.000  14.0000  5.475
## 62  6.40  9.8 32.730 2.675 103.1665  40.150  14.0000  5.475
## 63  7.83 11.7  4.083 1.328  18.0000   3.333   6.6670  5.475
## 116 9.70 10.8  0.222 0.406  10.0000  22.444  10.1110  5.475
## 161 9.00  5.8 32.730 0.900 142.0000 102.000 186.0000 68.050
## 184 8.00 10.9  9.055 0.825  40.0000  21.083  56.0910  5.475
## 199 8.00  7.6 32.730 2.675 103.1665  40.150 103.2855  5.475

Альтернативой “наивному” подходу является учет структуры связей между переменными. Например, можно воспользоваться тем, что между двумя формами фосфора oPO4 и PO4 существует тесная корреляционная связь. Тогда, например, можно избавиться от некоторых неопределенностей в показателе PO4, вычислив его пропущенные значения по уравнению простой регрессии:

data(algae)
lm(PO4 ~ oPO4, data = algae)

## 
## Call:
## lm(formula = PO4 ~ oPO4, data = algae)
## 
## Coefficients:
## (Intercept)         oPO4  
##      42.897        1.293

# Функция  вывода значений PO4 в зависимости от оPO4 
fillPO4 <- function(oP) {if (is.na(oP)) return(NA)
      else return(42.897 + 1.293 * oP)
}
# Восстановление пропущенных значений PO4
algae[is.na(algae$PO4), 'PO4'] <-
    sapply(algae[is.na(algae$PO4), 'oPO4'], fillPO4)
algae[ind, 10]

##  [1]  48.069   3.000   6.000   6.500   1.000   4.000   6.000  11.000
##  [9]   6.000  14.000  14.000   6.667  10.111 186.000  56.091      NA

Одно из пропущенных значений удалось восстановить.

Разумеется, легко придти к мысли не утруждать себя перебором всех возможных корреляций, а учесть все связи одновременно и целиком. Использование метода "bagImpute" осуществляет для каждой из имеющихся переменных построение множественной бутстреп-агрегированной модели, или бэггинг-модели (bagging), на основе деревьев регрессии, используя все остальные переменные в качестве предикторов. Этот метод мудр и точен, но требует значительных затрат времени на вычисление, особенно при работе с данными большого объема:

library(ipred)
data(algae)
pPbI <- preProcess(algae[, 4:11], method = 'bagImpute')
algae[, 4:11] <- predict(pPbI, algae[, 4:11])
(Imp.Bag <- algae[ind, 4:11])

##         mxPH     mnO2       Cl      NO3      NH4      oPO4      PO4
## 28  6.800000 11.10000  9.00000 0.630000  20.0000   4.00000  30.3218
## 38  8.000000 10.63080  1.45000 0.810000  10.0000   2.50000   3.0000
## 48  8.039073 12.60000  9.00000 0.230000  10.0000   5.00000   6.0000
## 55  6.600000 10.80000 14.55668 3.245000  10.0000   1.00000   6.5000
## 56  5.600000 11.80000 10.04778 2.220000   5.0000   1.00000   1.0000
## 57  5.700000 10.80000 10.04778 2.550000  10.0000   1.00000   4.0000
## 58  6.600000  9.50000 10.04778 1.320000  20.0000   1.00000   6.0000
## 59  6.600000 10.80000 12.40412 2.640000  10.0000   2.00000  11.0000
## 60  6.600000 11.30000 14.55668 4.170000  10.0000   1.00000   6.0000
## 61  6.500000 10.40000 21.51934 5.970000  10.0000   2.00000  14.0000
## 62  6.400000 10.69229 10.04778 1.854339 161.1671  15.08828  14.0000
## 63  7.830000 11.70000  4.08300 1.328000  18.0000   3.33300   6.6670
## 116 9.700000 10.80000  0.22200 0.406000  10.0000  22.44400  10.1110
## 161 9.000000  5.80000 82.65631 0.900000 142.0000 102.00000 186.0000
## 184 8.000000 10.90000  9.05500 0.825000  40.0000  21.08300  56.0910
## 199 8.000000  7.60000 47.50948 4.785011 242.2558  64.94436 181.1578
##          Chla
## 28   2.700000
## 38   0.300000
## 48   1.100000
## 55   4.890752
## 56   3.645598
## 57   4.346394
## 58   3.894385
## 59   4.346394
## 60   4.189956
## 61  14.476727
## 62   5.948531
## 63   3.193589
## 116 64.582758
## 161 68.050000
## 184  3.478534
## 199 11.283728

Наконец, третий метод функции preProcess() для заполнения пропусков - "knnImpute" - основан на простейшем, но чрезвычайно эффективном алгоритме k ближайших соседей (k-nearest neighbours) или kNN. В основе метода kNN лежит гипотеза о том, что тестируемый объект d будет иметь примерно тот же набор признаков, что и обучающие объекты в локальной области его ближайшего окружения (рис. 3.6).

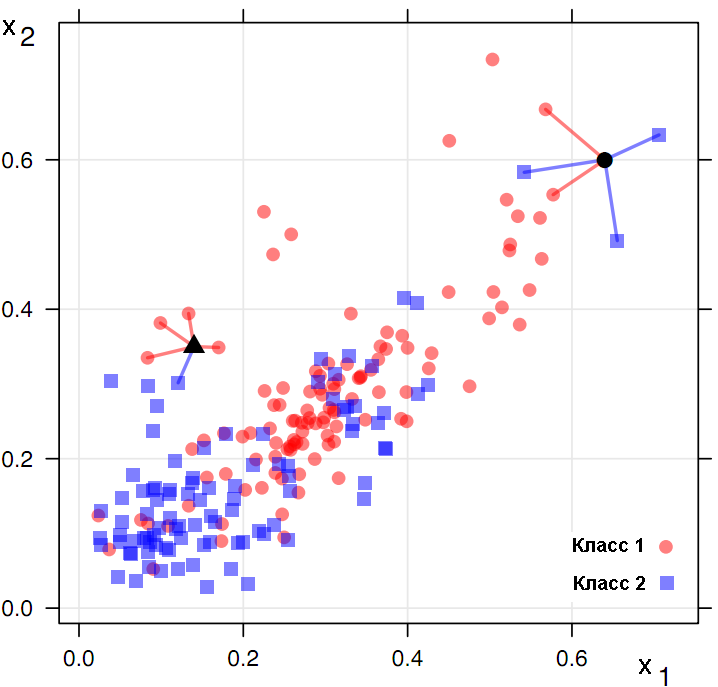
Рисунок 3.6: Интерпретация метода k ближайших соседей

Если речь идет о классификации, то неизвестный класс объекта определяется голосованием $k$ его ближайших соседей (на рис. 3.6 $k = 5$). kNN-регрессия оценивает значение неизвестной координаты $Y$, усредняя известные ее величины для тех же $k$ соседних точек.

Одна из важных проблем kNN - выбор метрики, на основе которой оценивается близость объектов. Наиболее общей формулой для подсчета расстояния в m-мерном пространстве между объектами $\mathbf{X_1}$ и $\mathbf{X_2}$ является мера Минковского: \[ D_S (\mathbf{X_1}, \mathbf{X_2}) = (\sum |x_{1i} - x_{2i}|^p )^{1/r},\]

где $i$ изменяется от 1 до $m$, а $r$ и $p$ - задаваемые исследователем параметры, с помощью которых можно осуществить нелинейное масштабирование расстояний между объектами. Мера расстояния по Евклиду получается, если принять в метрике Минковского $r = p = 2$, и является, по-видимому, наиболее общей мерой расстояния, знакомой всем со школы по теореме Пифагора. При $r = p = 1$ имеем “манхеттенское расстояние” (или “расстояние городских кварталов”), не столь контрастно оценивающее большие разности координат $x$. Вторая проблема метода kNN заключается в решении вопроса о том, на мнение какого числа соседей $k$ нам целесообразно положиться? В свое время мы обсудим этот вопрос детально, а сейчас будем ориентироваться на значение $k = 5$, используемое по умолчанию:

data(algae)
pPkI <- preProcess(algae[, 4:11], method = 'knnImpute')
alg.stand <- predict(pPkI, algae[, 4:11])

Получив в результате применения predict() матрицу переменных с пропущенными значениями, заполненными этим методом, мы с удивлением обнаруживаем, что данные оказались стандартизованными (т.е. центрированными и нормированными на стандартное отклонение). Но а как иначе можно было вычислить меру близости по переменным, измеренным в разных шкалах? Пришлось для возвращения в исходное состояние применить обратную операцию:

m <- pPkI$mean
sd <- pPkI$std
algae[, 4:11] <- t(apply(alg.stand, 1, function (r) m + r * sd))
(Imp.Knn <- algae[ind, 4:11])

##      mxPH  mnO2      Cl    NO3     NH4     oPO4      PO4    Chla
## 28  6.800 11.10  9.0000 0.6300  20.000   4.0000  21.2400  2.7000
## 38  8.000  9.92  1.4500 0.8100  10.000   2.5000   3.0000  0.3000
## 48  7.762 12.60  9.0000 0.2300  10.000   5.0000   6.0000  1.1000
## 55  6.600 10.80  7.4974 3.2450  10.000   1.0000   6.5000  3.1800
## 56  5.600 11.80  7.4974 2.2200   5.000   1.0000   1.0000  3.1800
## 57  5.700 10.80  6.0474 2.5500  10.000   1.0000   4.0000  0.8600
## 58  6.600  9.50  5.3422 1.3200  20.000   1.0000   6.0000  0.9000
## 59  6.600 10.80  7.4974 2.6400  10.000   2.0000  11.0000  3.1800
## 60  6.600 11.30  7.7774 4.1700  10.000   1.0000   6.0000  3.9400
## 61  6.500 10.40 11.8864 5.9700  10.000   2.0000  14.0000  4.4000
## 62  6.400 10.24  4.4074 1.1638  60.040   5.0300  14.0000  0.8600
## 63  7.830 11.70  4.0830 1.3280  18.000   3.3330   6.6670  1.0200
## 116 9.700 10.80  0.2220 0.4060  10.000  22.4440  10.1110  5.5000
## 161 9.000  5.80 58.5314 0.9000 142.000 102.0000 186.0000 68.0500
## 184 8.000 10.90  9.0550 0.8250  40.000  21.0830  56.0910  0.9400
## 199 8.000  7.60 59.7922 3.6018 320.908 115.1684 185.9664 12.3958

Наконец, зададимся следующим закономерным вопросом: а какой метод лучше? Обычно эта проблема не имеет теоретического решения, и исследователь полагается на собственную интуицию и опыт. Но мы можем оценить, насколько расходятся между собой результаты, полученные каждым способом заполнения. Для этого сформируем блок данных из $3 \times 16 = 48$ строк исходной таблицы с пропусками, заполненными тремя методами ("Med", "Bag", "Knn"), и выполним снижение размерности пространства переменных методом главных компонент в двумерное (см. раздел 2.4). Посмотрим, как “лягут карты” на плоскости (рис. 3.7):

ImpVal <- rbind(Imp.Med, Imp.Knn)
ImpVal <- rbind(ImpVal, Imp.Bag)
Imp.Metod <- as.factor(c(rep("Med", 16), rep("Knn", 16), rep("Bag", 16)))

library(vegan); library(RANN)
Imp.M <- rda(ImpVal ~ Imp.Metod, ImpVal)
plot(Imp.M, display = "sites", type = "p")
ordihull(Imp.M, Imp.Metod, draw = "polygon", alpha = 67, 
         lty = 2, col = c(1, 2, 3), label = TRUE)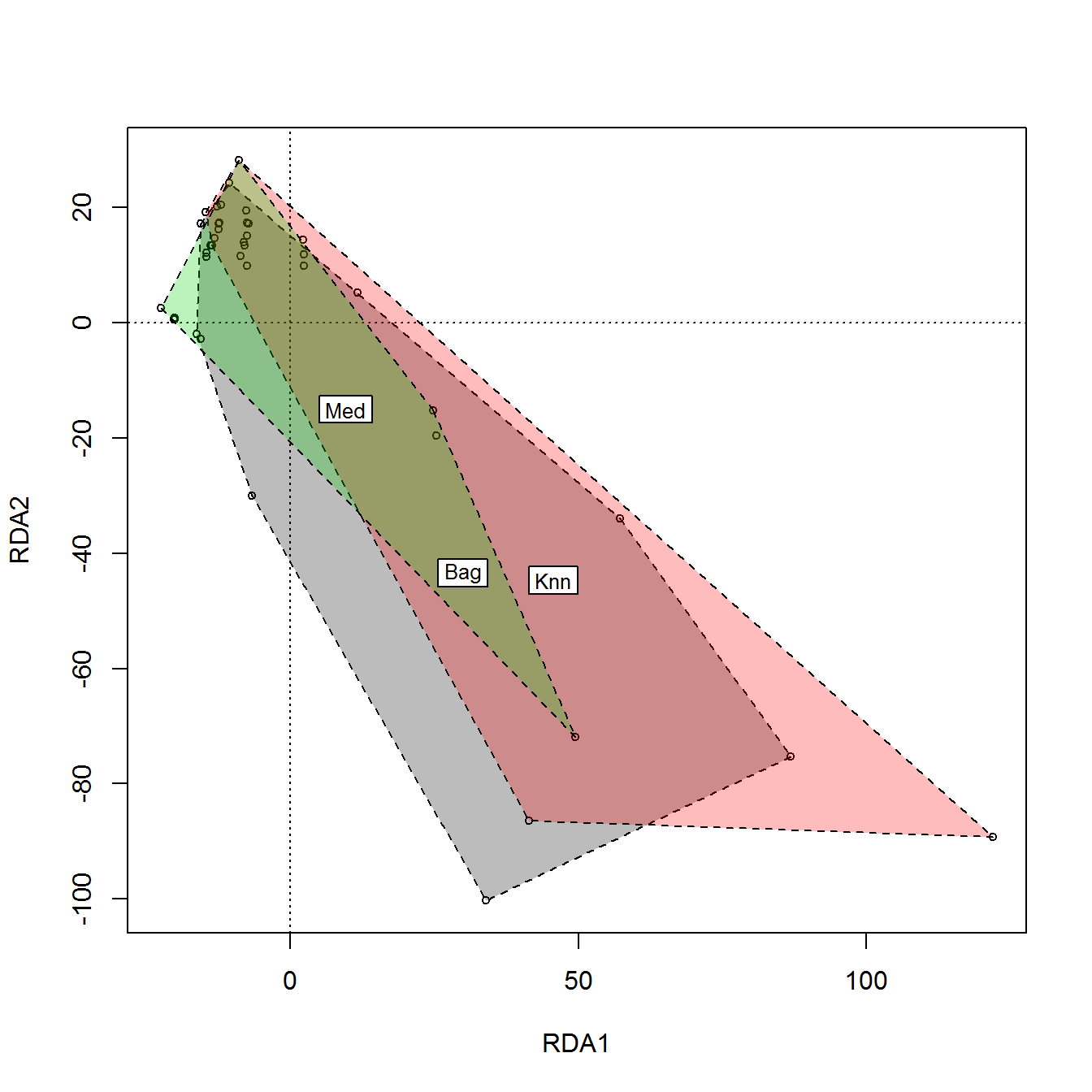

Рисунок 3.7: Ординационная диаграмма блоков данных таблицы algae с пропущенными значениями, заполненными разными способами

На рис. 3.7 мы выделили контуром (hull), проведенным через крайние точки, области каждого из трех блоков данных и поместили метку метода в центры тяжести полученных многоугольников. Понятно, что медианное заполнение характеризуется меньшей вариацией результатов, поскольку игнорирует специфичность свойств каждого объекта. Оба других метода, учитывающих внутреннюю структуру данных, дали приблизительно похожие результаты.