10.3 Оценка качества кластеризации
После создания кластерного решения обычно возникает вопрос, насколько оно устойчиво и статистически значимо. Здесь существует эмпирическое правило - устойчивая группировка должна сохраняться при изменении методов кластеризации: например, если результаты иерархического кластерного анализа имеют долю совпадений более 70% с группировкой по методу \(k\) средних, то предположение об устойчивости принимается.
В теоретическом плане проблема проверки адекватности кластеризации не решена, по крайней мере, без использования другого вида анализа или априорного знания принадлежности объектов к соответствующим классам. Авторы сборника Ким и др. (1989, с. 192 и далее) подробно рассматривают и в итоге отвергают пять методов проверки адекватности кластеризации (ru.wikipedia.org):
- Кофенетическая корреляция – не рекомендуется и ограниченна в использовании;
- Тесты на значимость разбиения данных на кластеры (многомерный дисперсионный анализ) – всегда дают значимый результат;
- Методика повторных (случайных) выборок – не доказывает обоснованность решения;
- Тесты значимости для признаков, не использованных при кластеризации, – пригодны только при наличии повторных измерений;
- Методы Монте-Карло очень сложны и доступны только опытным математикам.
С тех пор в литературе предложено множество методов и критериев оценки качества результатов кластеризации (clustering validation). Можно выделить несколько подходов к валидации11 кластеров (Kassambara, 2017):
- внешняя валидация, которая заключается в сравнении итогов кластерного анализа с заранее известным результатом (т.е. метки кластеров известны априори);
- относительная валидация, которая оценивает структуру кластеров, изменяя различные параметры одного и того же алгоритма (например, число групп \(k\));
- внутренняя валидация, которая использует внутреннюю информацию процесса объединения в кластеры (если внешняя информация отсутствует);
- оценка стабильности объединения в кластеры (или специальная версия внутренней валидации), использующая методы ресэмплинга.
Одна из проблем машинного обучения без учителя состоит в том, что методы кластеризации будут формировать группы, даже если анализируемый набор данных представляет собой полностью случайную структуру. Поэтому первой задачей валидации, которую рекомендуется выполнить перед началом кластерного анализа, является оценка общей предрасположенности имеющихся данных к объединению в кластеры (clustering tendency).
Статистика Хопкинса (Hopkins) является одним из индикаторов тенденции к группированию. Для ее расчета создается B псевдо-наборов данных, сгенерированных случайным образом на основе распределения с тем же стандартным отклонением, что и оригинальный набор данных. Для каждого наблюдения \(i\) из \(n\) рассчитывается среднее расстояние до \(k\) ближайших соседей: \(w_i\) между реальными объектами и \(q_i\) между искусственными объектами и их самыми близкими реальными соседями. Тогда статистика Хопкинса
\[H_{ind} = \frac{\sum_n w_i}{\sum_n q_i + \sum_n w_i},\]
превышающая 0.5, будет соответствовать нулевой гипотезе о том, что \(q_i\) и \(w_i\) подобны, а группируемые объекты распределены случайно и однородно. Величина \(H_{ind} < 0.25\) на 90%-нном уровне уверенности указывает на имеющуюся тенденцию к группированию данных.
Весьма полезна также визуальная оценка тенденции (VAT, Visual Assessment of cluster Tendency): потенциальные группы представлены темными квадратами вдоль главной диагонали “VAT-диаграммы”. Функция get_clust_tendency() из пакета factoextra попутно с графиком рассчитывает также и статистику Хопкинса:
library(cluster)
data("USArrests")
df.stand <- as.data.frame(scale(USArrests))
library("factoextra")
get_clust_tendency(df.stand, n = 30,
gradient = list(low = "steelblue", high = "white"))## $hopkins_stat
## [1] 0.386467
##
## $plot
Рисунок 10.10: Корреляция между кластеризациями на основе разных методов
В случае криминогенности штатов США мы имеем весьма умеренную склонность к образованию групп. В разделе 10.1 мы рассмотрели три метода выбора оптимального числа кластеров, которые не всегда давали однозначные оценки. “Но это еще не все…”. С помощью пакета NbClust можно найти оптимальную схему объединения в кластеры, используя ни много ни мало целых 30 индексов качества! При этом происходит перебор различных комбинаций числа групп, метрик дистанции и методов кластеризации:
library(NbClust)
nb <- NbClust(df.stand, distance = "euclidean", min.nc = 2,
max.nc = 8, method = "average", index = "all")nb$Best.nc## KL CH Hartigan CCC Scott Marriot TrCovW
## Number_clusters 8.0000 2.000 5.0000 2.000 5.0000 5.0 4.0000
## Value_Index 24.0818 43.462 12.3077 -0.141 43.9763 180497.5 383.4582
## TraceW Friedman Rubin Cindex DB Silhouette Duda
## Number_clusters 5.0000 6.0000 5.0000 4.0000 4.0000 2.0000 2.0000
## Value_Index 15.3518 2.8394 -0.5185 0.3713 0.7784 0.4085 1.0397
## PseudoT2 Beale Ratkowsky Ball PtBiserial Frey McClain
## Number_clusters 2.0000 2.0000 2.0000 3.0000 3.0000 1 2.000
## Value_Index -0.6878 -0.0874 0.4466 18.8709 0.6361 NA 0.547
## Dunn Hubert SDindex Dindex SDbw
## Number_clusters 8.0000 0 4.0000 0 8.0000
## Value_Index 0.2509 0 1.2638 0 0.1636fviz_nbclust(nb) + theme_minimal()## Among all indices:
## ===================
## * 2 proposed 0 as the best number of clusters
## * 1 proposed 1 as the best number of clusters
## * 8 proposed 2 as the best number of clusters
## * 2 proposed 3 as the best number of clusters
## * 4 proposed 4 as the best number of clusters
## * 5 proposed 5 as the best number of clusters
## * 1 proposed 6 as the best number of clusters
## * 3 proposed 8 as the best number of clusters
##
## Conclusion
## =========================
## * According to the majority rule, the best number of clusters is 2 .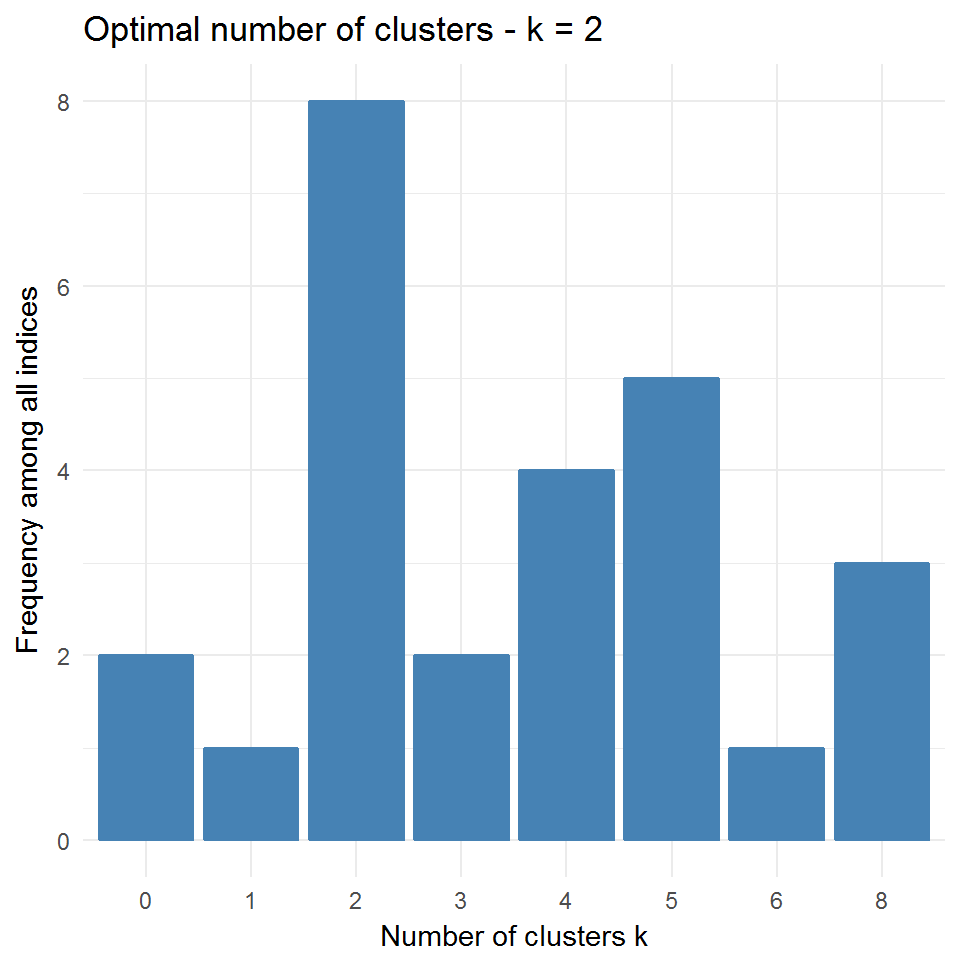
Рисунок 10.11: Оптимальное число кластеров по оценкам различных индексов
Разброс оценок числа классов наилучшего разбиения весьма велик: от 2 по индексу МакКлайна до 8 по индексу Данна, поэтому приходится прибегать к тривиальному голосованию.
Кофенетическую корреляцию можно также рассчитать между исходной матрицей дистанции и матрицей кофенетических расстояний, и тогда она может служить мерой адекватности кластерного решения исходным данным. Оценим по этому показателю пять иерархических кластеризаций, сравниваемых между собой в предыдущем разделе (Borcard et al., 2011):
d <- dist(df.stand, method = "euclidean")
library(vegan)
hc_list <- list(hc1 <- hclust(d,"com"),
hc2 <- hclust(d,"single"), hc3 <- hclust(d,"ave"),
hc4 <- hclust(d, "centroid"), hc5 <- hclust(d, "ward.D2"))
Coph <- rbind(
MantelStat <- unlist(lapply(hc_list,
function(hc) mantel(d, cophenetic(hc))$statistic)),
MantelP <- unlist(lapply(hc_list,
function(hc) mantel(d, cophenetic(hc))$signif)))
colnames(Coph) <- c("Complete", "Single", "Average", "Centroid", "Ward.D2")
rownames(Coph) <- c("W Мантеля", "Р-значение")
round(Coph, 3)## Complete Single Average Centroid Ward.D2
## W Мантеля 0.698 0.541 0.718 0.607 0.698
## Р-значение 0.001 0.001 0.001 0.001 0.001Таким образом, максимальное значение коэффициента W матричной корреляции Мантеля (а, следовательно, и наибольшая адекватность матрице расстояний, построенной по исходным данным) принадлежит кластеризации по методу средней связи. Нелишне заметить, что все рассмотренные кластеризации статистически значимы, т.е. не могут быть объяснены случайными причинами (впрочем, такое будет почти всегда). Наконец, Ким и др. (1989) не рекомендуют использовать кофенетическую корреляцию в основном по причине несоответствия кофенетических расстояний нормальному распределению. Можно, однако, привести массу аргументов, показывающих откровенную слабость этих утверждений.
После того, как мы попытались оценить, насколько хорошо топология дендрограммы отображает предрасположенность объектов к группированию, остаются некоторые вопросы, вызывающие несомненный интерес. Можно ли вычислить \(p\)-значения в целом для полученной иерархической кластеризации? Какие фрагменты древовидной структуры являются “слабым звеном” в полученной конструкции?
Однако правомерен и контрвопрос: “Нужно ли вычислять эти \(р\)-значения?” Как убедительно сказано в книге Джеймс и др. (2016), не существует правильных или неправильных результатов кластеризации, поскольку, по определению, это метод обучения без учителя. Все определяется соответствием полученного решения поставленной задаче, которая на практике в большинстве случаев сводится просто к тому, чтобы приблизительно оценить, на сколько групп целесообразно разделить данные. При этом степень этого соответствия всегда будет субъективной.
Ответ на второй вопрос об устойчивости фрагментов кластерной структуры состоит в том, чтобы взять из исходной таблицы множество повторных выборок, построить для каждой из них свою дендрограмму и вычислить частоту встречаемости каждого фрагмента в сформированной последовательности разбиений. Разумеется, здесь невозможно обойтись без бутстрепа, позволяющего подсчитать вероятность BP (Bootstrap Probability) встречаемости произвольного узла в бутстреп-копиях. Обычно фрагменты древовидной структуры считаются статистически значимыми, если с ветвями дерева связывается бутстреп-вероятность, превышающая 70-80%.
Х. Шимодейра (Shimodaira, 2002), сравнивая центры распределения исходной и бутстреп-выборок, показал, что величина BP является приближенной оценкой вероятности появления узла в дереве. Несмещенную оценку вероятности AU (Approximately Unbiased) можно получить, выполнив повторную серию бутстрепа в различных масштабах (multiscale bootstrap resampling). Для этого отдельно вычисляют BP-значения, формируя бутстреп-выборки разного объема: например, \(0.5n, 0.6n, \dots, 1.4n, 1.5n\), где \(n\) - объем исходной выборки. Несмещенная бутстреп-вероятность AU находится аппроксимацией ряда полученных значений BP. Оптимальные оценки AU для каждого кластера дендрограммы, найденные путем подбора параметрических моделей с использованием метода максимального правдоподобия, могут быть получены с использованием пакетов pvclust и scaleboot для R.
Некоторая проблема заключается в том, что функция pvclust(), ориентированная на генетические исследования, выполняет кластеризацию признаков (т.е. столбцов таблицы данных), а для 4 показателей нашей демонстрационной таблицы USArrests это особого интереса не представляет. Если попробовать выполнить анализ с транспонированной матрицей \(4 \times 60\), выполнив команду pvclust(t(USArrests)), то решение найти нельзя из-за проблем с сингулярными преобразованиями:
Error in solve.default(crossprod(X, X/vv)),
system is exactly singular: U[2, 2] = 0Воспользуемся тогда в качестве примера набором Boston из пакета MASS, включающим 14 признаков привлекательности 506 участков города для проживания (рис. 10.12):
data(Boston, package = "MASS")
library(pvclust)
set.seed(123)
# Бутстреп деревьев и расчет BP- и AU- вероятностей для узлов
boston.pv <- pvclust(Boston, nboot = 100, method.dist = "cor",
method.hclust = "average", quiet = TRUE)
plot(boston.pv) # дендрограмма с p-значениями
pvrect(boston.pv) # выделение боксами достоверных фрагментов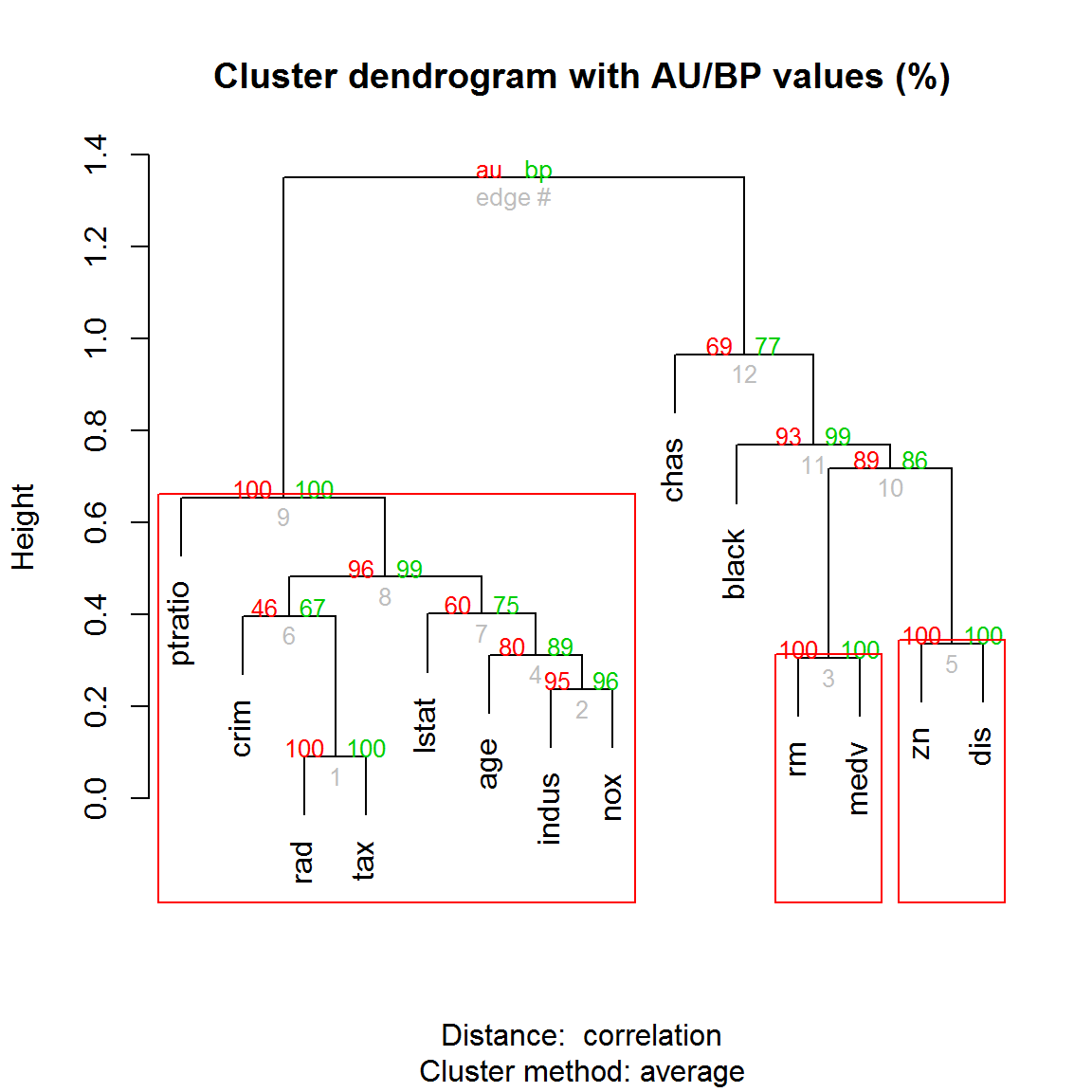
Рисунок 10.12: Дендрограмма с нанесенными значениями AU/BP для каждого узла
Этот пример показывает, что с практической точки зрения кластеризация признаков (переменных) может быть столь же важна, как и группировка объектов. Использование коэффициентов корреляции для расчета матрицы дистанций method.dist = "cor" избавляет нас от необходимости стандартизовать данные.
При анализе дендрограммы на рис. 10.12 можно увидеть, что признаки иногда образуют кластеры с ясно интерпретируемой зависимостью (“среднее число комнат в жилье rm” и “медианная стоимость дома medv”), но часто их тесная связь нуждается в дополнительном осмыслении (“индекс доступности к кольцевым дорогам rad” и “сумма налога на недвижимость tax”, или “доля участков, продаваемых в розницу indus” и “концентрация окислов азота nox”). В целом была получена весьма стабильная кластеризация: наименее низкую бутстреп-вероятность имеют такие важнейшие признаки, как “криминальный индекс crim” и “процент жителей с низким социальным статусом lstat”, которые вполне могут объединиться в группу с любым другим из имеющихся показателей (например, “долей афроамериканцев black”).
Мы используем термин “валидность”, чтобы избегнуть некоторой двусмысленности таких понятий как “адекватность”, “эффективность”, “значимость”.↩