ГЛАВА 6 Пакет prophet

Прогнозирование — это, пожалуй, самая распространенная задача, возникающая при работе с временными рядами. Однако получить надежные прогнозы непросто — для этого требуется серьезная подготовка специалиста, который решает подобную задачу, а также наличие подходящего (и желательно удобного в использовании) программного обеспечения.

В R существует большое количество пакетов для анализа временных рядов (см. также сайт проф. Роба Хиндмана). Например, одним из наиболее популярных является пакет forecast, в котором реализованы как классические (экспоненциальное сглаживание, модель Хольта–Винтерса, ARIMA и др.), так и недавно разработанные методы прогнозирования (модели для сгруппированных временных рядов, рядов с несколькими сезонными компонентами и др.). Такое разнообразие методов является и преимуществом, и недостатком пакета forecast. Другой важный недостаток состоит в том, что все реализованные в forecast методы имеют свои собственные параметры настройки, и даже опытные аналитики не застрахованы от выбора неправильного метода и/или набора параметров для решения стоящей задачи.

В 2017 г. специалисты компании Facebook объявили о разработанном ими новом пакете для прогнозирования временных рядов — prophet (“пророк”). prophet во многом лишен указанных выше недостатков forecast и других подобных пакетов и позволяет создавать точные прогнозные модели в (полу–)автоматическом режиме. В этой главе мы рассмотрим основные возможности prophet и особенности работы с ним.

Пакет prophet распространяется бесплатно по лицензии MIT. Его легко установить стандартным образом из хранилища CRAN (на Windows–машинах предварительно нужно будет установить Rtools):

Если вы работаете на компьютере Mac под управлением OS X, не забудьте добавить аргумент type = "source":

6.1 Методология

Подробное описание реализованной в prophet методологии можно найти в статье Taylor and Letham (2017). Вкратце, в основе этой методологии лежит процедура подгонки аддитивных регрессионных моделей (Generalized Additive Models, GAM) следующего вида: \[y(t) = g(t) + s(t) + h(t) + \epsilon_t,\] где \(g(t)\) и \(s(t)\) — функции, аппроксимирующие тренд ряда и сезонные колебания (например, годовые, недельные и т.п.) соответственно, \(h(t)\) — функция, отражающая эффекты праздников и других влиятельных событий, а \(\epsilon_t\) — нормально распределенные случайные возмущения. Для аппроксимации перечисленных функций используются следующие методы:

  • тренд: кусочная линейная регрессия или кусочная логистическая кривая роста;
  • годовая сезонность: частичные суммы ряда Фурье, число членов которого (порядок) определяет гладкость функции;
  • недельная сезонность: представлена в виде индикаторной переменной;
  • “праздники” (например, официальные праздничные и выходные дни — Новый год, Рождество и т.п., а также другие дни, во время которых свойства временного ряда могут существенно измениться — спортивные или культурные события, природные явления и т.п.): представлены в виде индикаторных переменных.

Оценивание параметров подгоняемой модели выполняется с использованием принципов байесовской статистики (либо методом нахождения апостериорного максимума (MAP), либо путем полного байесовского вывода). Для этого применяется платформа вероятностного программирования Stan. Пакет prophet представляет собой ни что иное, как удобный интерфейс для работы с этой платформой из среды R (имеется также аналогичная библиотека для Python — fbprophet).

6.2 Первый простой пример

Для иллюстрации особенностей работы с пакетом prophet воспользуемся набором данных bitcoin, в котором хранятся исторические данные по стоимости биткоина на момент закрытия торгов (подразд. 1.5.2). Стоимость биткоина — не самая простая переменная для моделирования (что справедливо для подавляющего большинства финансовых временных рядов). Этот ряд обладает сложным трендом, дисперсия его значений возрастает со временем, имеют место резкие изменения уровней, вероятно сопряженные с какими–то (в большинстве случаев неизвестными нам) особыми событиями (рис. 1.3). Тем не менее, это хороший пример реальных данных, с которыми аналитик может столкнуться на практике. Тем интереснее будет посмотреть, как с задачей прогнозирования этого ряда справится prophet!

Предположим, что нам необходимо сделать прогноз стоимости биткоина на следующие 90 дней. Приведенный ниже код выполняет подготовку данных для построения подобной модели: сначала происходит логарифмирование значений стоимости биткоина y (для снижения дисперсии), а затем разбиение исходной выборки на обучающую (все наблюдения за исключением последних 90 дней) и проверочную (последние 90 дней).

Обратите внимание также на замену класса итоговых таблиц bitcoin_train и bitcoin_test с tsibble на стандартный data.frame — это обусловлено тем, что в настоящее время функции пакета prophet, к сожалению, не могут корректно работать с данными в формате tsibble.

Подгонку моделей с разными параметрами мы будем выполнять на обучающих данных (bitcoin_train). Проверочная выборка (bitcoin_test) пригодится в самом конце процесса моделирования, чтобы выяснить насколько наши ожидания в отношении качества выбранной оптимальной модели соответствуют действительности. Заметьте, что в обеих этих таблицах столбец с датами обозначен как ds, а столбец со значениями отклика как y. Это условные обозначения, принятые в prophet. Использование каких–либо других имен приведет к ошибке при вызове соответствующих функций.

Обучающие данные, подготовленные описанным выше способом, представлены на рис. 6.1.

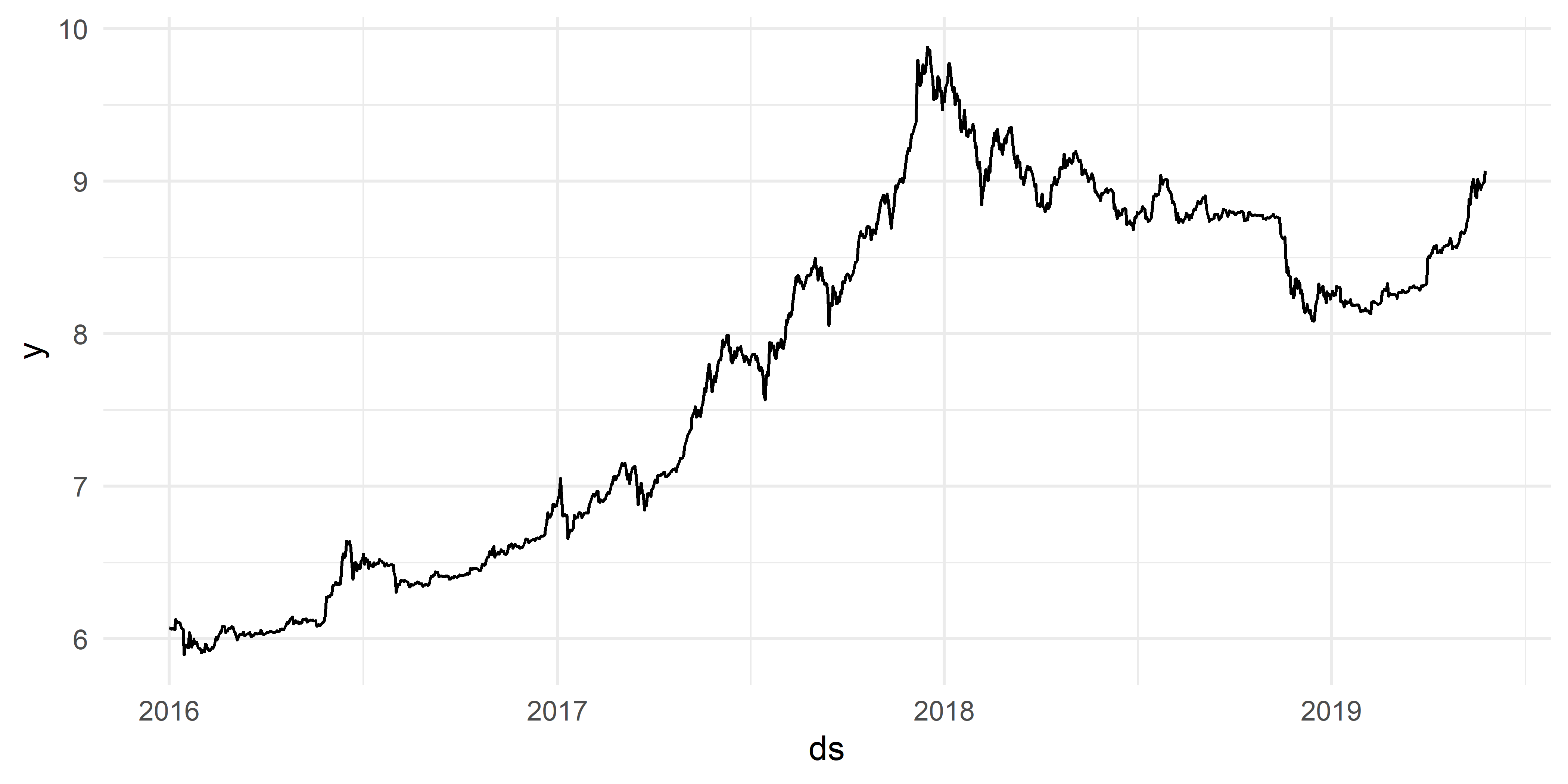
Обучающие данные по стоимости биткоина

РИСУНОК 6.1: Обучающие данные по стоимости биткоина

Нашу первую модель (обозначим ее M0) мы построим с использованием параметров, принятых в prophet по умолчанию. Для этого потребуется всего одна строка кода:

Объект M0 представляет собой большой список (выполните команду str(M0), чтобы просмотреть его структуру). Для получения прогноза на основе этой модели необходимо сначала воспользоваться функцией make_future_dataframe() и создать таблицу с датами, охватывающими необходимый временной промежуток в будущем (“горизонт”), а затем подать эту таблицу вместе с модельным объектом на функцию predict():

Объект forecast_M0 — это обычная таблица, в которой хранятся значения нескольких рассчитанных на основе модели M0 величин, включая компоненты модели (см. разд. 6.1), предсказанные значения отклика, а также верхние и нижние границы доверительных интервалов соответствующих величин. Вот так, например, выглядят первые несколько предсказанных значений стоимости биткоина и их (принятые по умолчанию) 80%–ные доверительные границы:

##       yhat yhat_lower yhat_upper
## 1 6.134964   6.024296   6.230752
## 2 6.134025   6.034873   6.237148
## 3 6.127710   6.026591   6.232882
## 4 6.124329   6.018906   6.227581
## 5 6.119314   6.008620   6.227911
## 6 6.111687   6.006040   6.218552

Таблицу forecast_M0 и объект M0 далее можно подать на функцию plot(), чтобы изобразить подогнанную модель и прогнозные значения на графике (рис. 6.2):

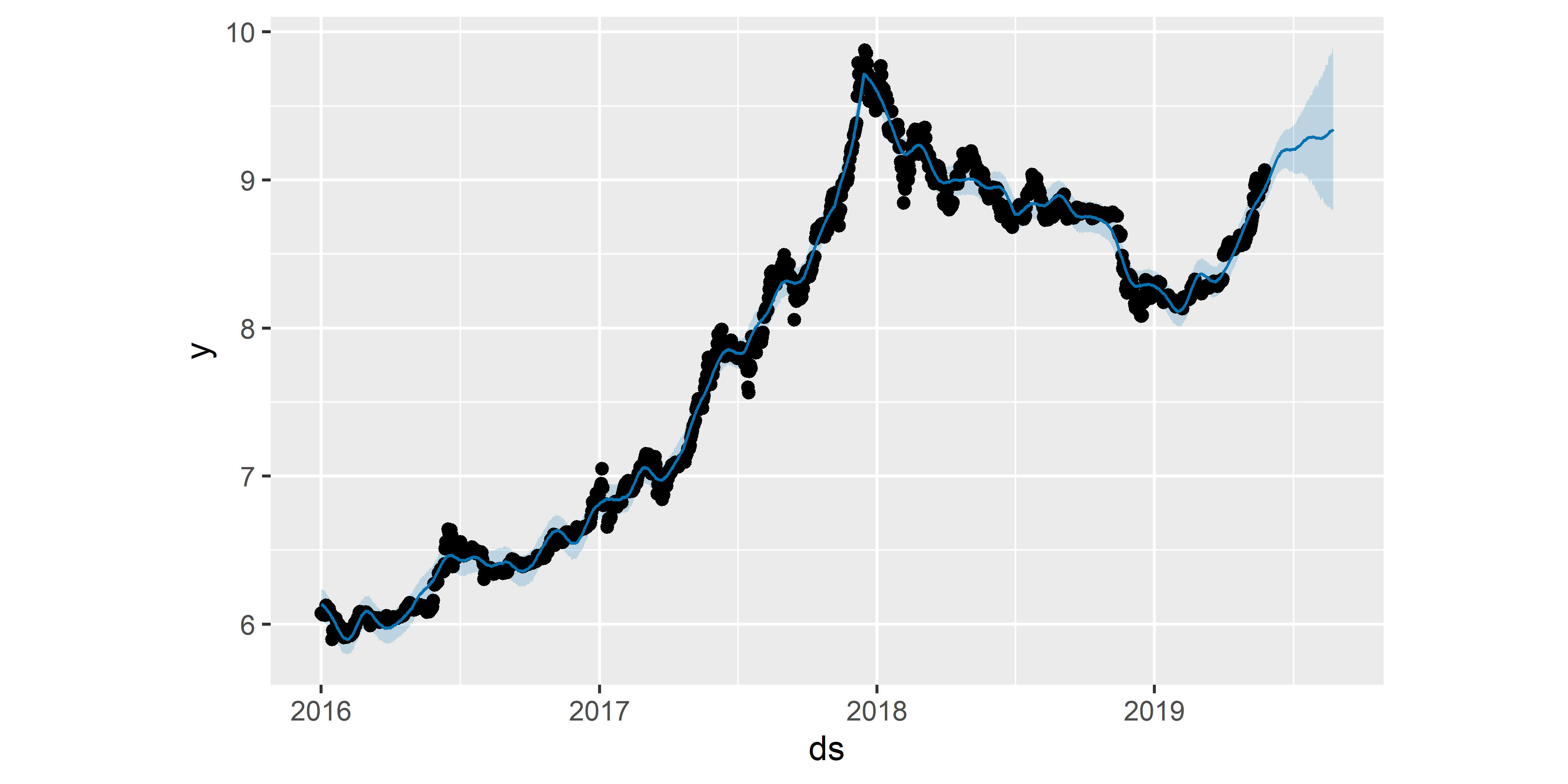
Прогноз стоимости биткоина, полученный на основе модели M0

РИСУНОК 6.2: Прогноз стоимости биткоина, полученный на основе модели M0

Точки на рис. 6.2 соответствуют (логарифмированным) значениям стоимости биткоина из обучающей выборки. Сплошная голубая линия — это предсказанные моделью значения стоимости, а огибающая эту линию светло–голубая “лента” обозначает 80%–ные доверительные границы предсказанных значений. Прогнозные значения у на следующие 90 дней видны в правой части графика.

С помощью функции prophet_plot_components() мы можем также изобразить отдельные компоненты модели (рис. 6.3):

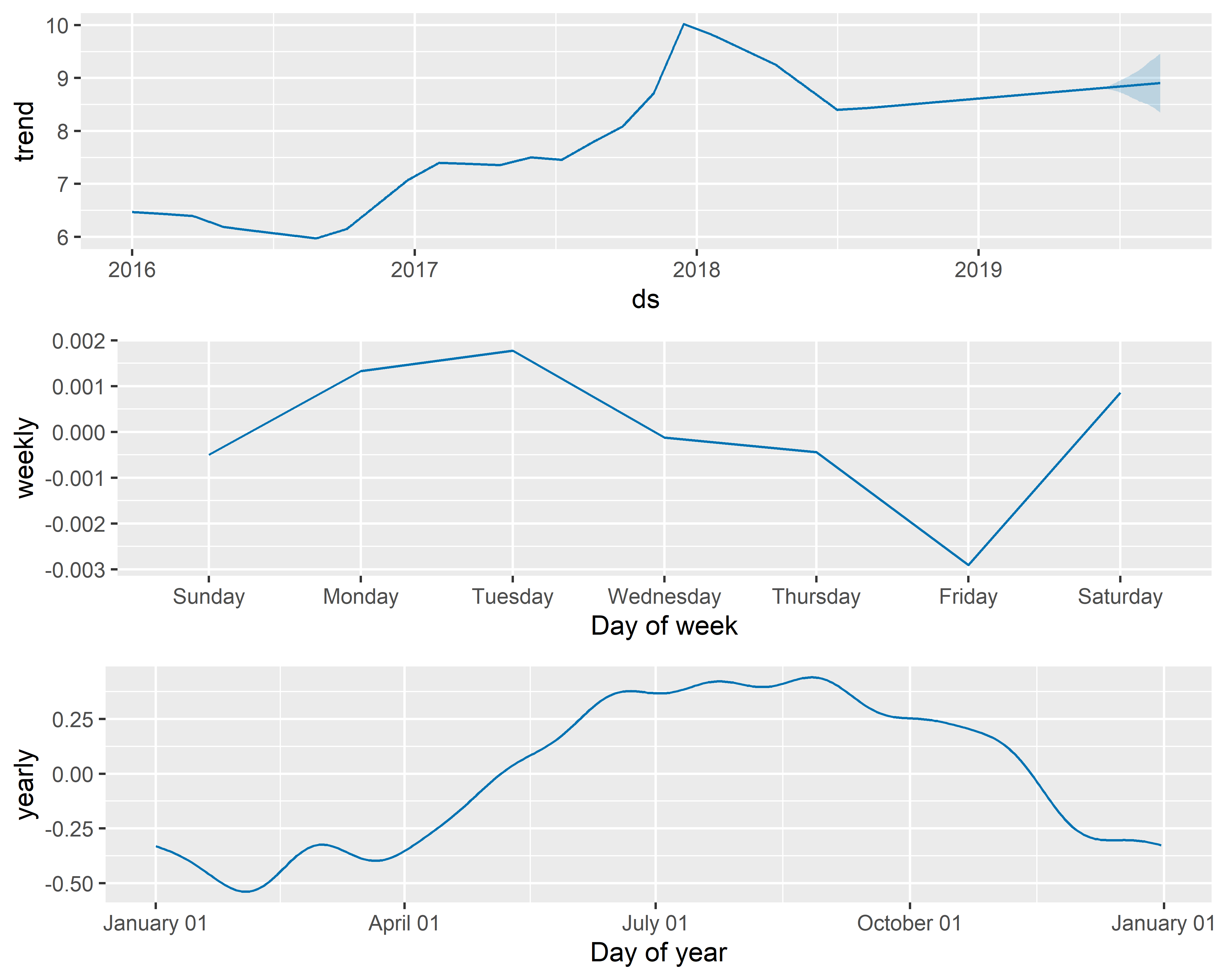
Компоненты модели M0

РИСУНОК 6.3: Компоненты модели M0

На рис. 6.3 видно, что модель M0 хорошо передает имеющийся в данных сложный тренд. Видно также, что в этом временном ряду есть очень слабо выраженные внутригодовые колебания и практически несуществующие колебания в пределах недели (обратите внимание на шкалы ординат этих трех графиков, которые помогают оценить вклад каждой из компонент).

Для создания модели M0 потребовалась всего одна строка кода и процесс подгонки занял пару секунд. Учитывая, что анализируемый нами временной ряд не самый простой для моделирования, полученная модель довольно хорошо передает свойства этого ряда. Возможность быстро и удобно создавать такие качественные модели в автоматическом режиме является основным преимуществом prophet.

Тем не менее, качество прогноза M0 оставляет желать лучшего. На данном этапе моделирования главным признаком неудовлетворительного качества предсказаний M0 является чрезмерно расширяющиеся доверительные границы прогнозных значений (рис. 6.3). В следующих разделах мы постараемся улучшить эту базовую модель путем добавления предикторов и настройки параметров функции prophet().

6.3 Функция prophet()

Ниже приведено описание основных аргументов функции prophet(), с которой мы познакомились в предыдущем разделе:

  • df — необязательный аргумент, с помощью которого указывают таблицу с историческими данными. Такая таблица должна содержать как минимум два столбца: ds (даты в формате YYYY-MM-DD) и y (значения моделируемого отклика). В случаях, когда тренд в y моделируется как логистический рост, таблица с историческими данными должна также содержать столбец cap (“емкость”), который соответствует максимально достижимым значениям y для соответствующих дат. Если аргумент df не указан (NULL), то произойдет только инициализация модельного объекта, а для непосредственного запуска подгонки модели необходимо будет воспользоваться функцией fit.profit(m, df).
  • growth — тип тренда. Принимает два возможных значения: "linear" (“линейный”, присвоено по умолчанию) и "logistic" (“логистический”).
  • changepoints — текстовый вектор с датами (в формате YYYY-MM-DD), соответствующими “переломным моментам”, или “точкам излома” в y (т.е. датам, когда произошли существенные изменения в тренде временного ряда). Если вектор changepoints не указан, то такие переломные моменты будут оценены автоматически.
  • n.changepoints — предполагаемое количество “переломных моментов” (25 по умолчанию). Если аргумент changepoints задан, то аргумент n.changepoints будет проигнорирован. Если же changepoints не задан, то n.changepoints потенциальных точек излома будут распределены равномерно в пределах исторического отрезка, задаваемого аргументом changepoint.range.
  • changepoint.range — доля исторических данных (начиная с самого первого наблюдения), по которым будут оценены точки излома. По умолчанию составляет 0.8 (т.е. 80% наблюдений).
  • yearly.seasonality — параметр настройки годовой сезонности (т.е. закономерных колебаний в пределах года). Принимает следующие возможные значения: "auto" (автоматический режим, принят по умолчанию), TRUE, FALSE или количество членов ряда Фурье, с помощью которого аппроксимируется компонента годовой сезонности.
  • weekly.seasonality — параметр настройки недельной сезонности (т.е. закономерных колебаний в пределах недели). Возможные значения те же, что и у yearly.seasonality.
  • daily.seasonality — параметр настройки дневной сезонности (т.е. закономерных колебаний в пределах дня). Возможные значения те же, что и у yearly.seasonality.
  • holidays — таблица, содержащая два обязательных столбца: holiday (текстовая переменная с названиями “праздников” и других важных событий, потенциально влияющих на свойства временного ряда) и ds (даты). По желанию в такую таблицу можно добавить еще два столбца — lower_window и upper_window, которые задают отрезок времени вокруг соответствующего события. Так, например, при "lower_window = -2" в модель будут добавлены 2 дня, предшествующие соответствующему событию. По желанию можно также добавить столбец prior_scale — априорное значение стандартного отклонения (нормального) распределения, с помощью которого моделируется эффект того или иного события.
  • seasonality.mode — режим моделирования сезонных компонент. Принимает два возможных значения: "additive" (аддитивный, задан по умолчанию) и "multiplicative" (мультипликативный).
  • seasonality.prior.scale — параметр, определяющий выраженность сезонных компонент модели (10 по умолчанию). Более высокие значения приведут к более “гибкой” модели, а низкие — к модели со слабее выраженными сезонными эффектами. Этот параметр можно задать отдельно для каждого типа сезонности с помощью функции add_seasonality().
  • holidays.prior.scale — параметр, определяющий выраженность эффектов “праздников” и других важных событий (10 по умолчанию). Если таблица, подаваемая на аргумент holidays, имеет столбец prior_scale (см. выше), то аргумент holidays.prior.scale будет проигнорирован.
  • changepoint.prior.scale — параметр, задающий чувствительность автоматического механизма обнаружения точек излома в тренде временного ряда y (0.05 по умолчанию). Более высокие значение позволят иметь больше таких точек излома (что одновременно увеличит риск переобучения модели).
  • mcmc.samples — целое число (0 по умолчанию). Если >0, то параметры модели будут оценены путем полного байесовского анализа с использованием mcmc.samples итераций алгоритма MCMC (процесс подгонки модели при этом может существенно замедлиться).
  • interval.width — число, определяющее ширину доверительного интервала для предсказанных моделью значений (0.8 по умолчанию, что соответствует 80%–ному интервалу). При "mcmc.samples = 0" этот интервал будет оценен с использованием MAP–метода и только на основе неопределенности в отношении тренда в у. Если же mcmc.samples >0, то доверительные интервалы будут оцениваться с учетом неопределенности в отношении оценок всех параметров модели (включая сезонные компоненты).
  • uncertainty.samples — число итераций для оценивания доверительных интервалов (1000 по умолчанию).
  • fit — логическое значение (TRUE по умолчанию). При fit = FALSE произойдет только инициализация модельного объекта, но подгонка модели не запустится.
  • ... — дополнительные параметры, которые передаются на функцию fit.prophet().

6.4 Точки излома тренда

Как было отмечено в предыдущем разделе, аналитик может задать точки излома либо самостоятельно (с помощью аргумента changepoints функции prophet()), либо довериться их автоматическому обнаружению. Рассмотрим, как работает каждый из этих режимов, и что происходит в результате изменения соответствующих аргументов функции prophet().

В автоматическом режиме при инициализации модели 25 потенциальных точек излома равномерно распределяются в пределах интервала, который охватывает первые 80% наблюдений из обучающей выборки. Именно это произошло, когда мы построили базовую модель М0 в разд. 6.2. Однако эти 25 точек — лишь предполагаемые места существенных изменений в тренде: в большинстве случаев на практике тренд временного ряда не изменяется так часто. Поэтому в ходе подгонки модели срабатывает механизм регуляризации (подобный \(l1\)–регуляризации), в результате чего выбирается минимально необходимое количество точек излома. Изобразить эти автоматически обнаруженные точки излома можно с помощью функции add_changepoints_to_plot(). Так, для модели M0 получаем (рис. 6.4):

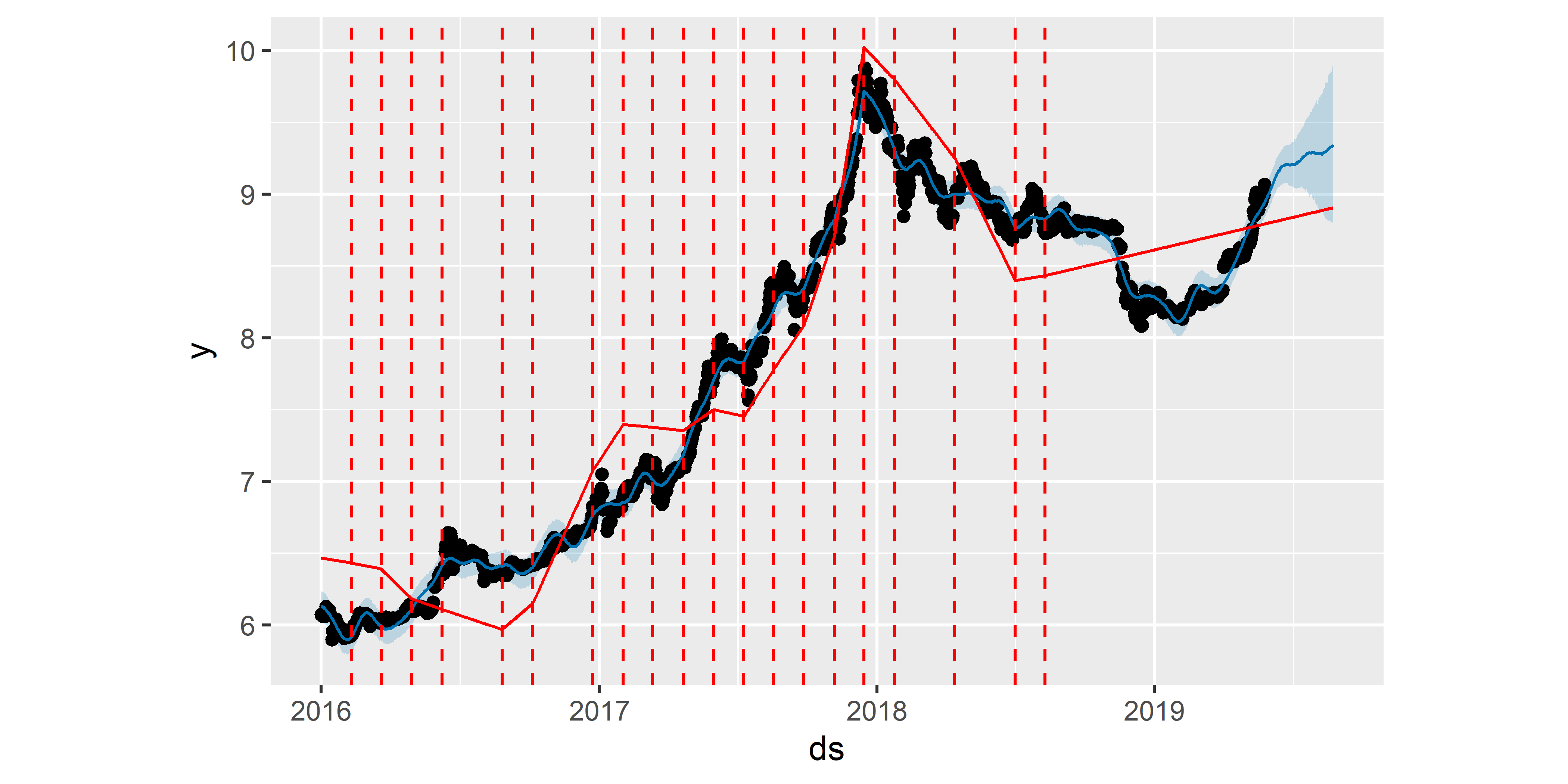
Точки излома тренда, оцененные в результате подгонки модели M0. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

РИСУНОК 6.4: Точки излома тренда, оцененные в результате подгонки модели M0. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

Судя по полученному графику, модель M0 все еще переоценивает количество “переломных моментов” в тренде. Построим новую модель, которая будет инициализирована с меньшим начальным количеством потенциальных точек излома (15 вместо 25; рис. 6.5):

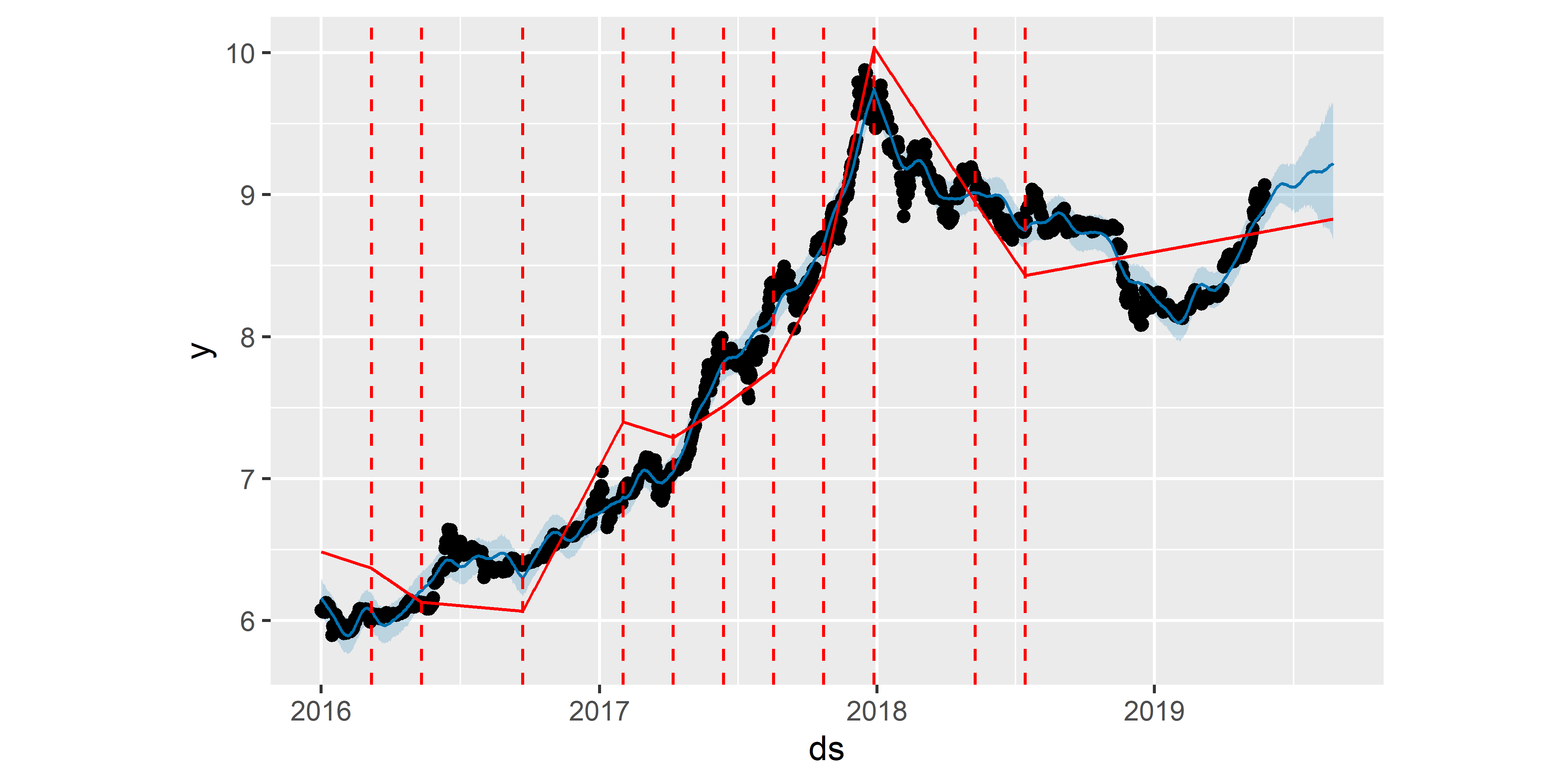
Точки излома тренда, оцененные в результате подгонки модели M1. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

РИСУНОК 6.5: Точки излома тренда, оцененные в результате подгонки модели M1. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

Как и ожидалось, оцененный тренд получился более гладким, чем в модели M0. Хорошо это или плохо, мы узнаем позже, когда рассмотрим диагностику качества моделей с помощью перекрестной проверки (разд. 6.8).

Помимо изменения начального количества потенциальных точек излома тренда мы можем также изменить временной интервал, в пределах которого происходит их оценивание. По умолчанию этот интервал охватывает первые 80% наблюдений. Однако из приведенных выше графиков видно, что примерно в начале ноября 2018 г. произошло резкое падение стоимости биткоина. Ни одна из построенных нами моделей пока не учла это изменение, поскольку оно не вошло в интервал, в пределах которого происходило оценивание точек излома. Увеличим этот интервал до 90%, воспользовавшись аргументом changepoint.range (одновременно увеличим количество потенциальных точек излома с 15 до 20, поскольку на большем промежутке времени можно ожидать больше перепадов в тренде):

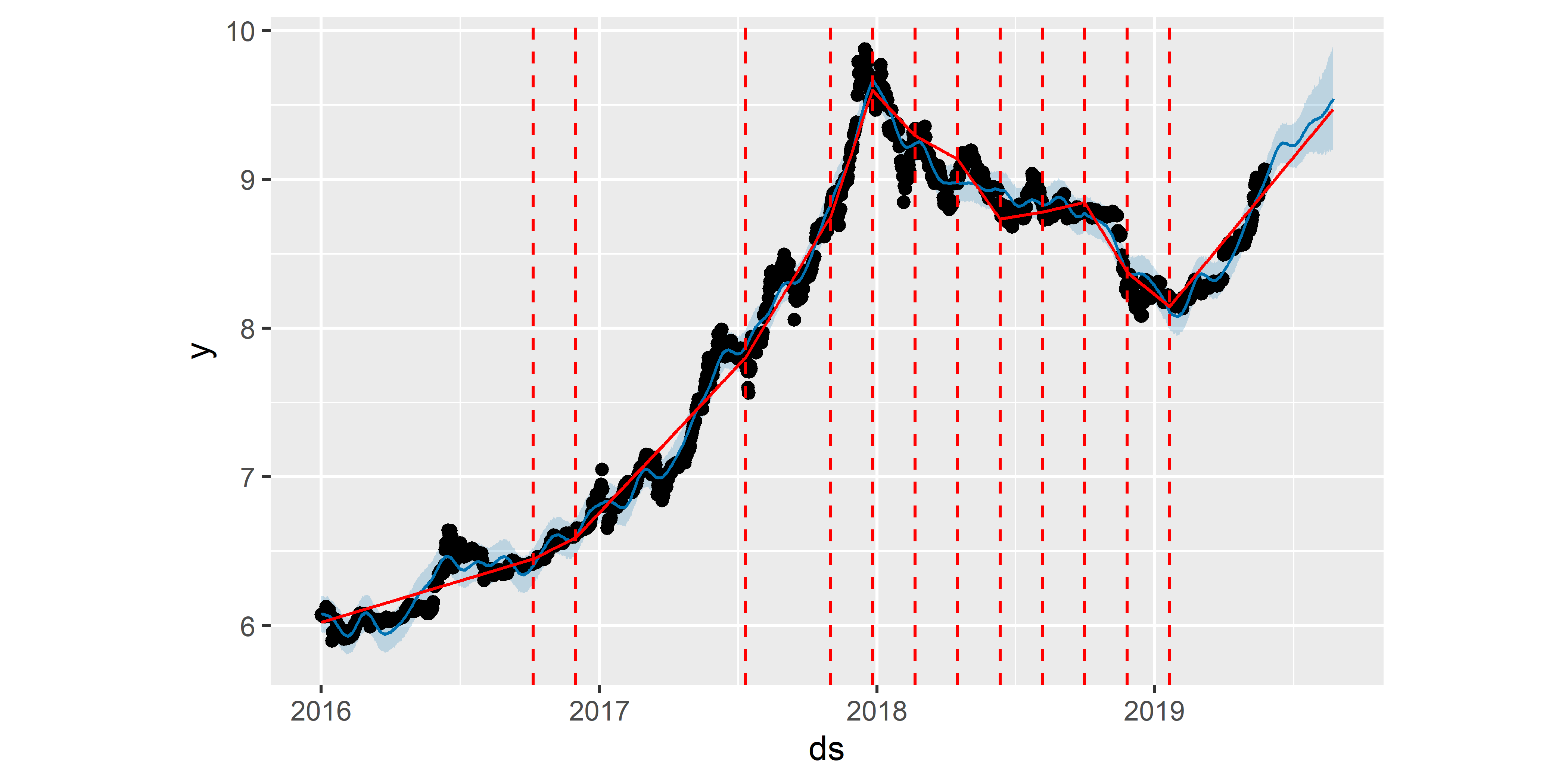
Точки излома тренда, оцененные в результате подгонки модели M2. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

РИСУНОК 6.6: Точки излома тренда, оцененные в результате подгонки модели M2. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

Как видно на рис. 6.6, полученная модель M2 намного лучше передает свойства анализируемого временного ряда. Это касается и получаемого с ее помощью прогноза (как с точки зрения направления тренда, так и с точки зрения ширины доверительных границ предсказанных значений).

Еще один параметр для настройки гладкости тренда в моделируемом временном ряду — это changepoint.prior.scale. Чем больше значение этого параметра (по сравнению с принятым по умолчанию значением 0.05), тем больше точек излома останется в полученной модели. Рассмотрим эффект действия changepoint.prior.scale на следующем примере (рис. 6.7):

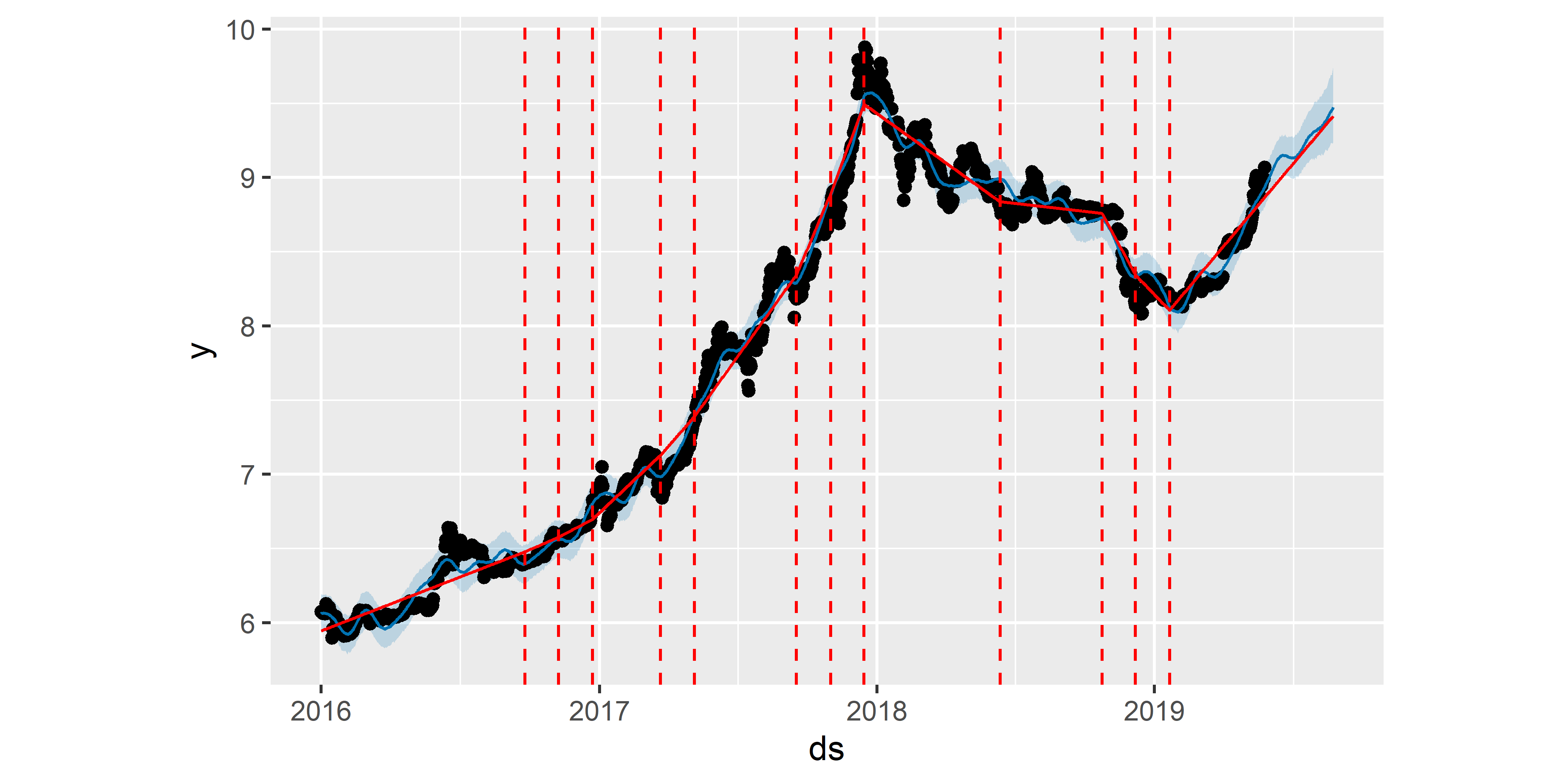
Точки излома тренда, оцененные в результате подгонки модели M3. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

РИСУНОК 6.7: Точки излома тренда, оцененные в результате подгонки модели M3. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

Как видим, модели M2 и M3 дают похожие результаты, что скорее определяется значением параметра changepoint.range, нежели способом регуляризации количества точек излома.

Наконец, посмотрим, что получится, если задать точки излома тренда “вручную”, а не оценивать их в автоматическом режиме. Для этого служит аргумент changepoints (рис. 6.8):

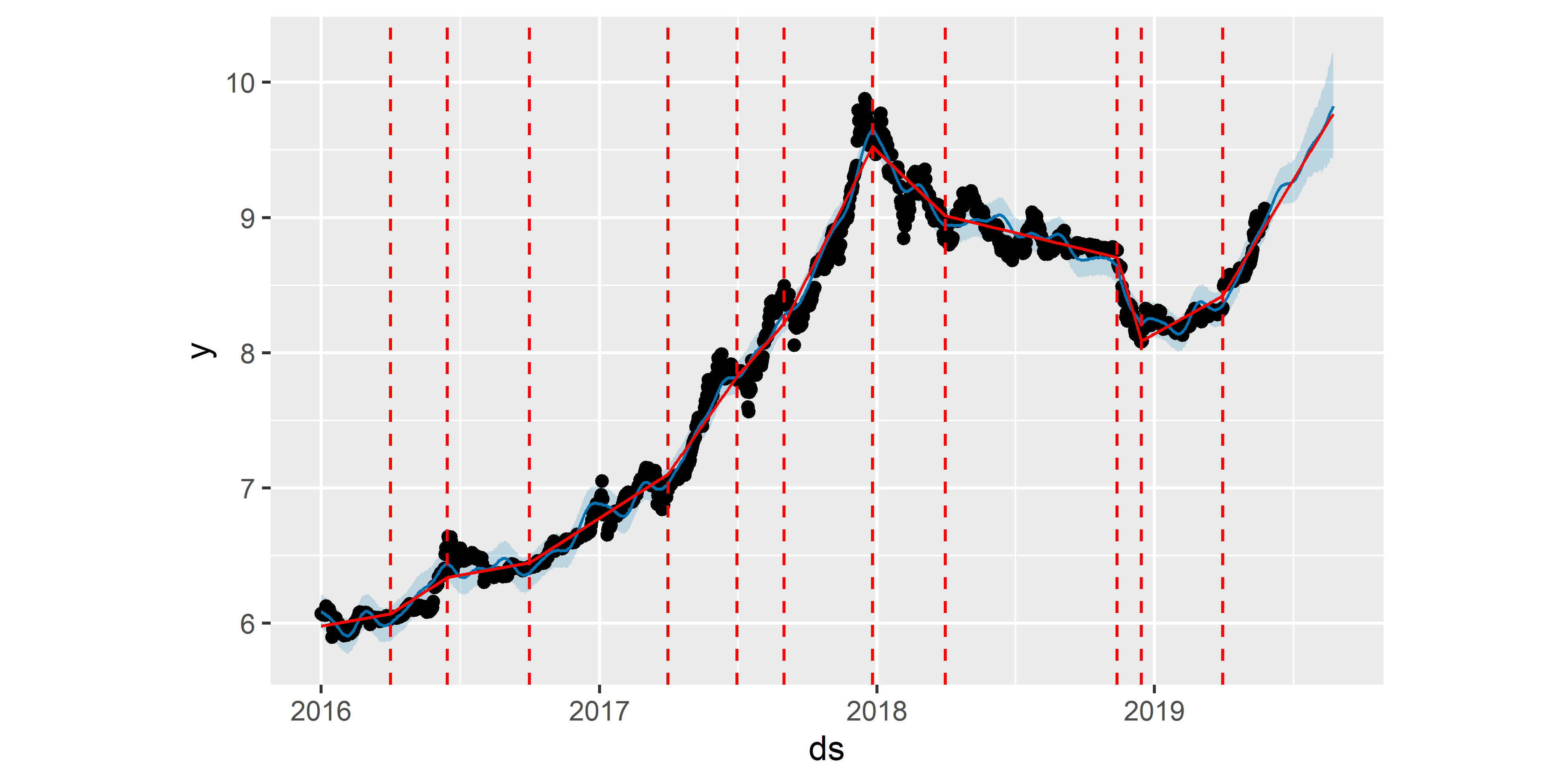
Точки излома тренда, оцененные в результате подгонки модели M4. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

РИСУНОК 6.8: Точки излома тренда, оцененные в результате подгонки модели M4. Сплошная красная линия — тренд. Штриховые красные линии — точки излома тренда

Модель M4 хорошо описывает тренд в анализируемом временном ряду, хотя не исключено, что она несколько переобучена.

6.5 Эффекты праздников и других важных событий

Продолжим начатое ранее знакомство с параметрами функции prophet() и рассмотрим способы моделирования эффектов “праздников”. Употребляемый здесь термин “праздник” — результат прямого перевода термина “holiday”, принятого в пакете prophet. Под этим термином мы будем понимать как настоящие официальные праздничные и выходные дни (например, Новый год, Рождество и т.п.), так и другие события, сопровождающиеся заметными изменениями свойств временного ряда (спортивные или культурные мероприятия, природные явления, политические события и т.п.). Поэтому слова “праздник” и “событие” будут применяться ниже как синонимы.

6.5.1 Формат представления

Как было отмечено в разд. 6.3, для добавления эффектов праздников в prophet–модель необходимо сначала создать отдельную таблицу, содержащую как минимум два обязательных столбца: holiday (названия праздников и других событий) и ds (временные метки; обычно это даты в формате YYYY-MM-DD). Важно, чтобы в такую таблицу входил как исторический период, на основе которого происходит обучение модели, так и период в будущем, для которого необходимо сделать прогноз. Например, если какое–то важное событие встречается в обучающих данных, то его следует указать и для прогнозного периода (при условии, конечно, что мы ожидаем повторение этого события в будущем, и что дата этого события входит в прогнозный период).

История биткоина полна событий, которые косвенно или непосредственно оказали влияние на стоимость этой криптовалюты (см. также [здесь](https://en.wikipedia.org/wiki/History_of_bitcoin)). В качестве примера, возьмем некоторые из этих событий:

Теперь добавим эти события в модель (аргумент holidays):

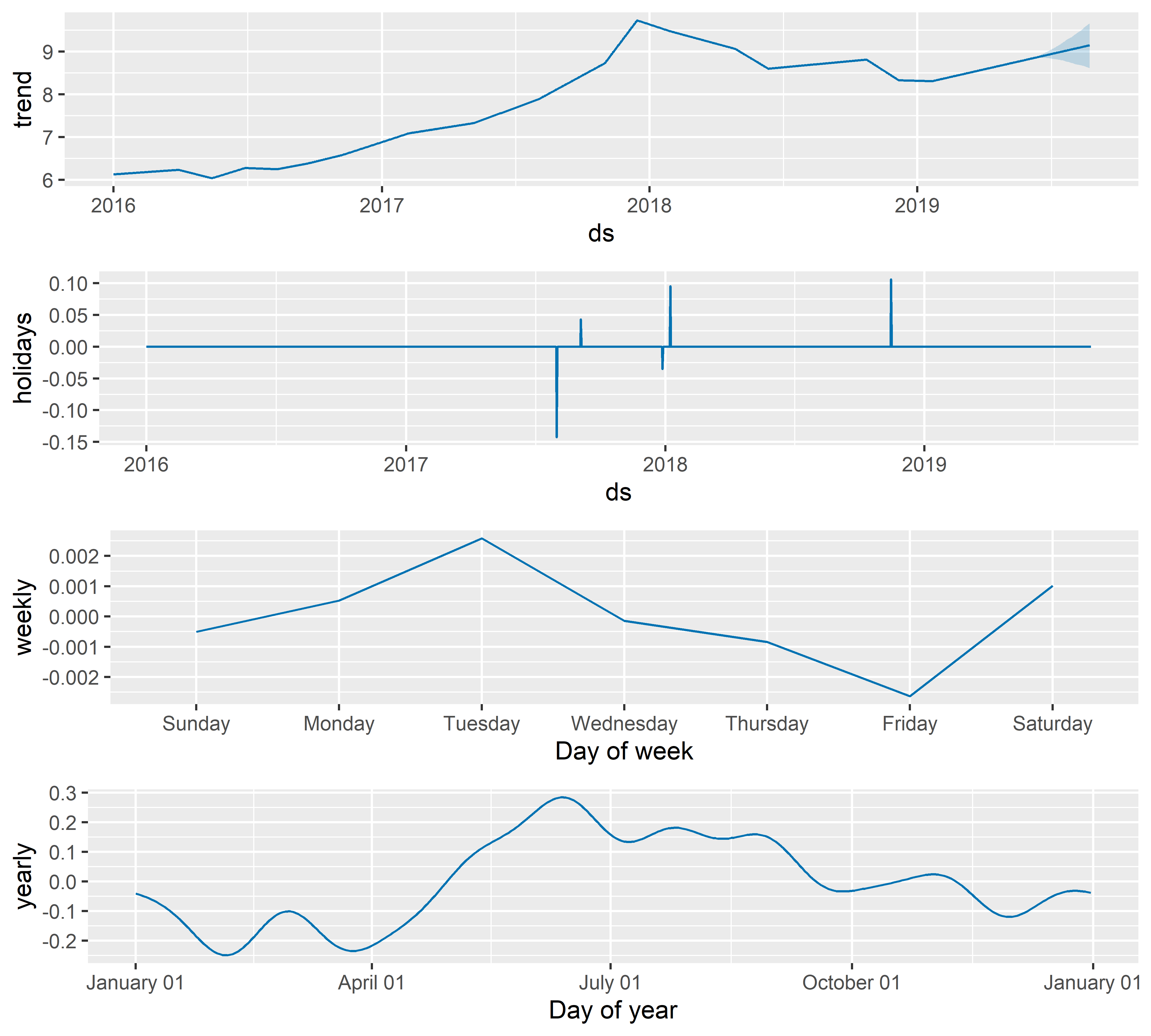
Оцененные компоненты модели M5

РИСУНОК 6.9: Оцененные компоненты модели M5

На рис. 6.9 приведены оцененные компоненты модели M5, включая эффекты событий, которые были добавлены с помощью аргумента holidays (см. второй график сверху). Функция plot_forecast_component() позволяет изобразить эффекты отдельных событий (см. аргумент name; рис. 6.10):

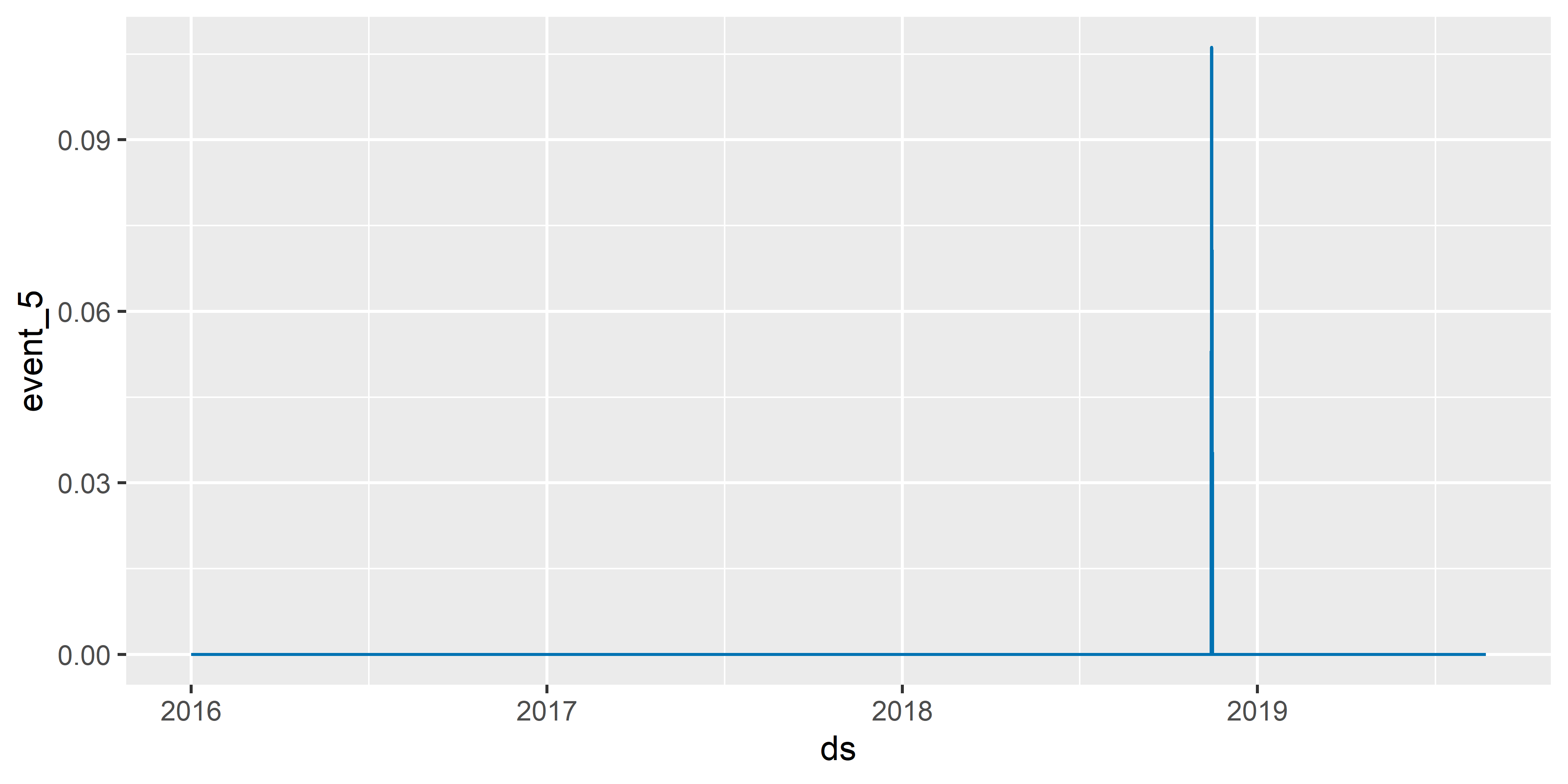
Эффект разветвления Bitcoin Cash на Bitcoin Cash SV и Bitcoing Cash ABC (event_5), оцененный с помощью модели M5

РИСУНОК 6.10: Эффект разветвления Bitcoin Cash на Bitcoin Cash SV и Bitcoing Cash ABC (event_5), оцененный с помощью модели M5

На аргумент name функции plot_forecast_component() можно также подать значение "holidays", что приведет к изображению на отдельном графике эффектов всех включенных в модель событий (рис. 6.11):

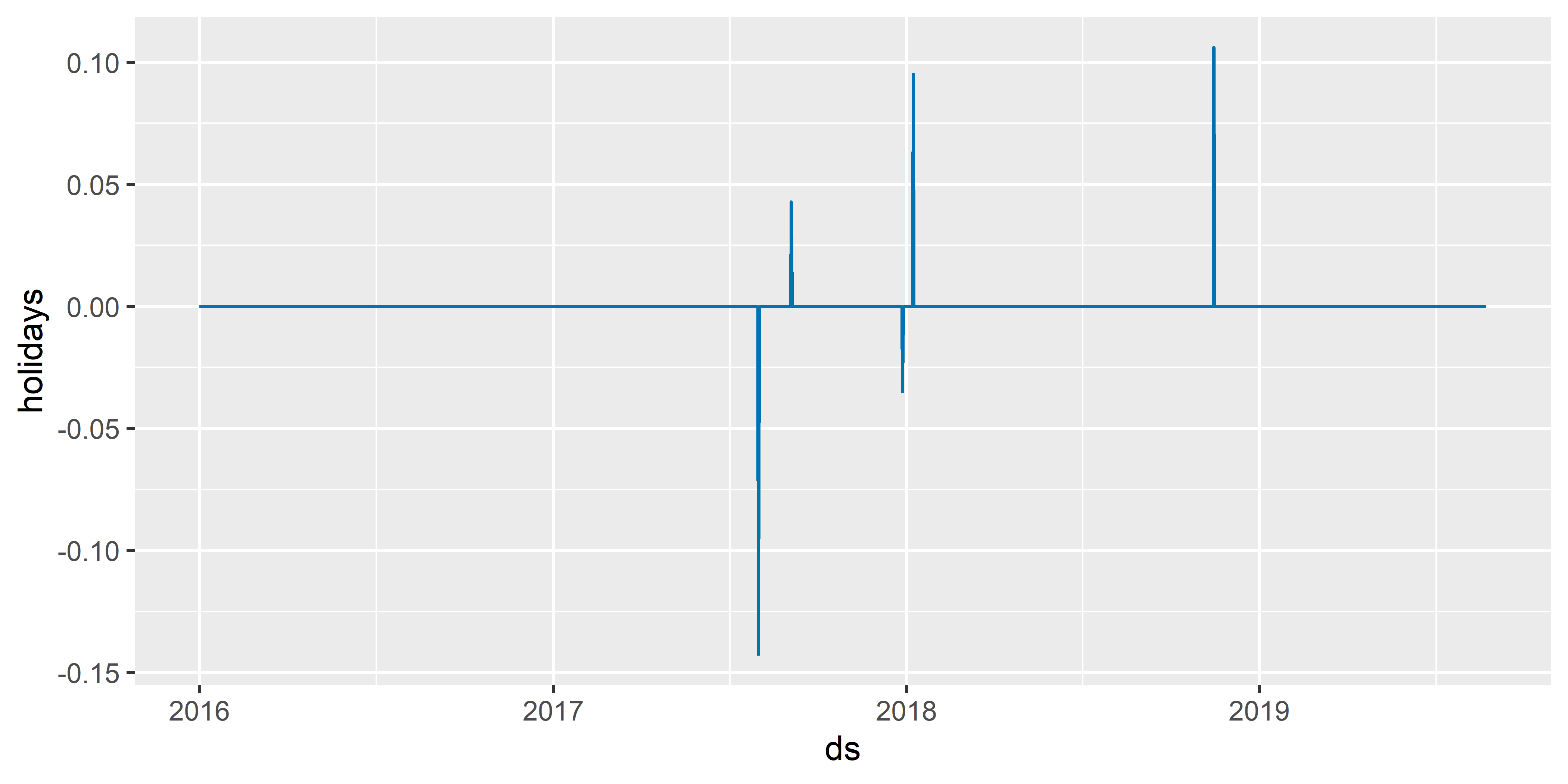
Эффекты всех событий, включенных в модель M5

РИСУНОК 6.11: Эффекты всех событий, включенных в модель M5

О наступлении некоторых событий в истории биткоина было известно заранее, как например о разветвлении Bitcoin Cash на Bitcoin Cash SV и Bitcoin Cash ABC (event_5 в модели M5). Поэтому многие спекулянты начали скупать Bitcoin Cash за несколько дней до “вилки”, или “форка”, чтобы впоследствии удвоить свой капитал (при наступлении “форка” владелец старой монеты автоматически становится владельцем и новой монеты). В связи с этим имело бы смысл моделировать event_5 как событие c “предысторией”, т.е. как событие, чей эффект начал проявлять себя за несколько дней до главной даты (в данном случае 15 ноября 2018 г.). В пакете prophet это можно сделать, добавив в таблицу с моделируемыми событиями столбцы lower_window (определят длительность “предыстории”) и upper_window (определяет длительность эффекта после главной даты). Для примера предположим, что спекулянты начали скупать Bitcoin Cash за две недели до “вилки” (lower_window = -14) и прекратили делать это сразу после “вилки” (upper_window = 0):

Эффект события с предысторией

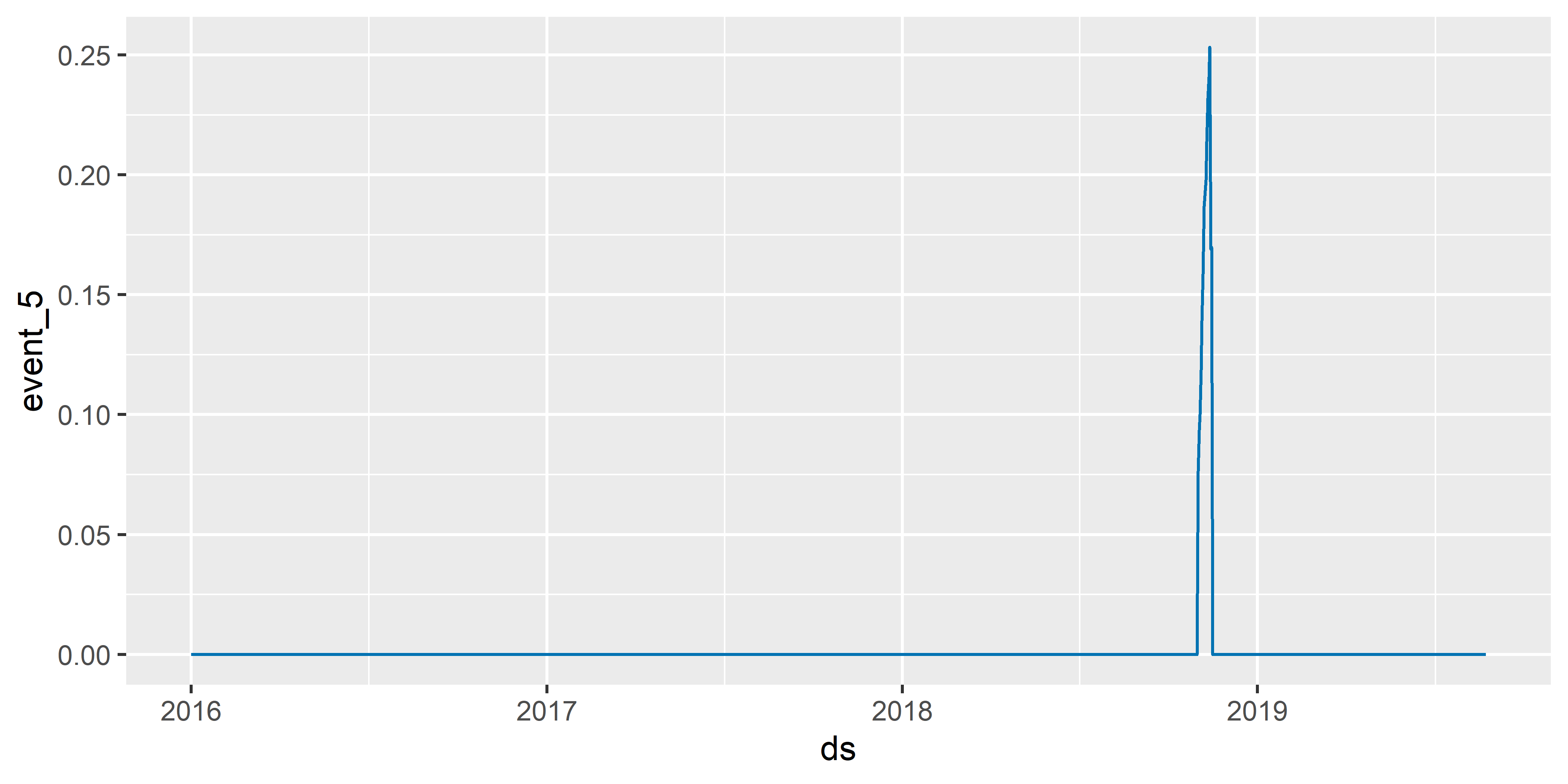
РИСУНОК 6.12: Эффект события с предысторией

Как видно на рис. 6.12, теперь эффект event_5 включает несколько дней до главной даты этого события (сравните с рис. 6.10).

6.5.2 Встроенные даты праздников

До этого момента мы моделировали эффекты событий, которые случались только один раз. Однако многие события, такие как официальные государственные праздники и выходные дни, повторяются регулярно и их эффекты также могут оказаться важными для прогноза.

Конечно, мы могли бы воспользоваться описанным выше способом для включения таких событий в модель, т.е. путем создания таблицы, подобной key_dates или key_dates2. К счастью, в большинстве случаев в этом не будет необходимости — в prophet уже включены даты официальных праздников и выходных дней для более чем 60 стран (полный список можно найти на сайте с официальной документацией по пакету). Эти встроенные даты праздников охватывают период с 1995 по 2044 гг. Для их добавления в модель служит функция add_country_holidays(), которая принимает два аргумента: m (модельный объект) и country_name (международное обозначение страны, например "Russia" или "RU"). Для примера построим модель, которая включает как рассмотренные выше важные в истории биткоина разовые события, так и регулярные официальные праздники США:

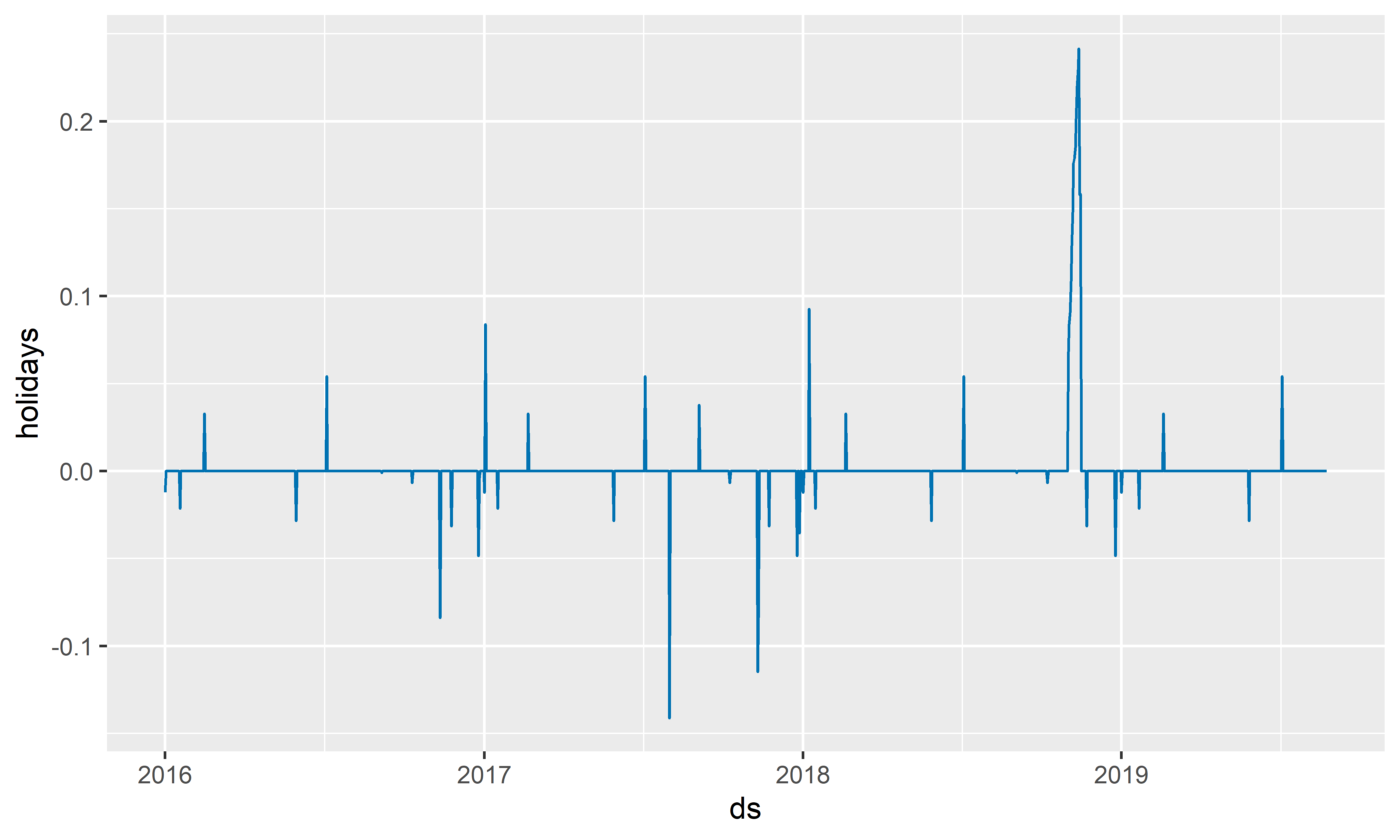
Эффекты разовых событий и официальных праздников США, оцененные с помощью модели M7

РИСУНОК 6.13: Эффекты разовых событий и официальных праздников США, оцененные с помощью модели M7

Оцененные эффекты всех событий из модели M7 показаны на рис. 6.13. Просмотреть названия этих событий можно следующим образом:

##  [1] "event_1"                     "event_2"                    
##  [3] "event_3"                     "event_4"                    
##  [5] "event_5"                     "New Year's Day"             
##  [7] "Martin Luther King, Jr. Day" "Washington's Birthday"      
##  [9] "Memorial Day"                "Independence Day"           
## [11] "Labor Day"                   "Columbus Day"               
## [13] "Veterans Day"                "Thanksgiving"               
## [15] "Christmas Day"               "Christmas Day (Observed)"   
## [17] "New Year's Day (Observed)"   "Veterans Day (Observed)"

6.5.3 Регуляризация

В пакете prophet имеется возможность подавлять величину эффектов “праздников”, что может оказаться полезным при возникновении риска переобучения модели. Такой контроль (регуляризация) осуществляется одним из двух способов:

  • глобальный контроль — распространяется на все моделируемые события;
  • контроль на уровне отдельных событий.

Аргумент holidays.prior.scale функции prophet() позволяет реализовать первый из этих способов. Данный аргумент задает априорное значение стандартного отклонения (нормального) распределения, с помощью которого моделируется эффект того или иного события. По умолчанию holidays.prior.scale = 10, что соответствует незначительной регуляризации. Уменьшение этого заданного по умолчанию значения приведет к подавлению эффектов всех событий, включенных в модель (рис. 6.14):

Эффекты событий до (модель M7) и после (модель M8) глобальной регуляризации

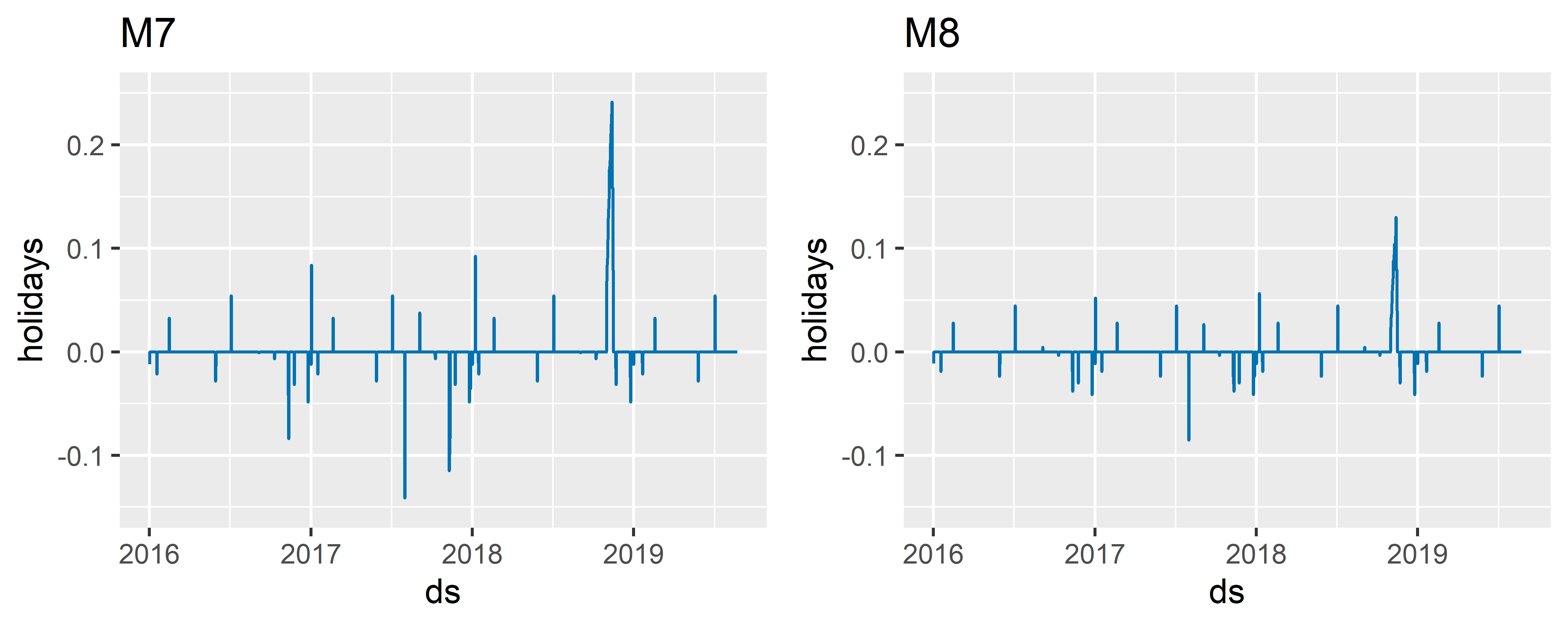
РИСУНОК 6.14: Эффекты событий до (модель M7) и после (модель M8) глобальной регуляризации

Для управления эффектами отдельных событий в таблицу с перечнем событий необходимо добавить столбец prior_scale. В качестве примера уменьшим величину эффекта события event_5, оставив остальные уровни без изменений (т.е. используя принятое по умолчанию значение параметра prior_scale = 10):

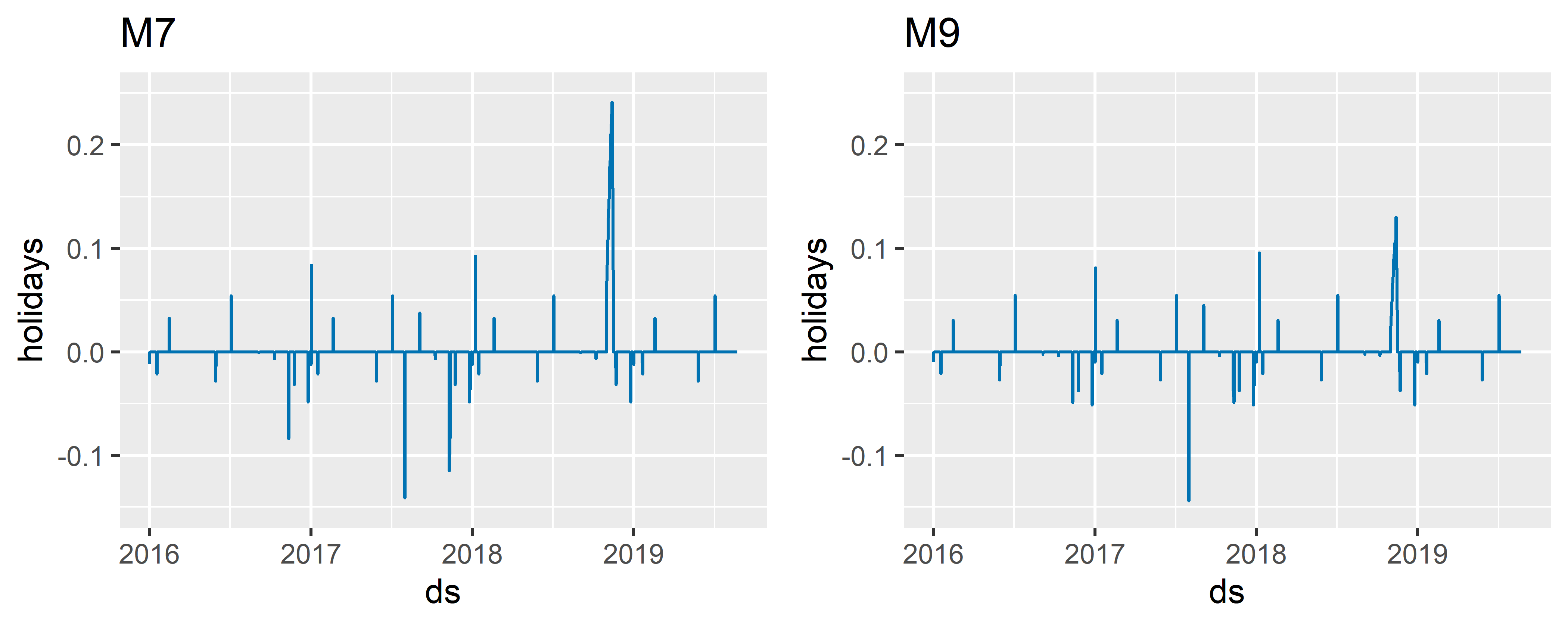
Пример регуляризации эффекта отдельного события

РИСУНОК 6.15: Пример регуляризации эффекта отдельного события

На рис. 6.15 хорошо виден результат подавления эффекта события event_5 (сравните уровень самого большого пика на графике слева с уровнем пика в той же позиции на графике справа). При этом эффекты большинства других событий и официальных праздников остались почти неизменными.

6.6 Сезонные компоненты

Как было отмечено в разд. 6.1, сезонные компоненты аппроксимируются в prophet с помощью частичных сумм ряда Фурье, число членов которого (порядок) определяет гладкость соответствующей функции. Рассмотрим различные способы спецификации сезонных колебаний.

6.6.1 Годовая, недельная и дневная компоненты

Функция prophet() имеет три аргумента, с помощью которых можно контролировать гладкость функций годовой, недельной и дневной сезонности: yearly.seasonality, weekly.seasonality и daily.seasonality (см. разд. 6.3). Увеличение значений этих аргументов приведет к подгонке менее гладких функций соответствующих компонент (что одновременно увеличит риск переобучения модели). На рис. 6.16 для примера показана функция годовой сезонности, оцененная с помощью модели M3 из разд. 6.4 (график этой функции построен с помощью служебной функции plot_yearly(), которую можно вызвать только обычным в таких случаях образом, т.е. указав имя пакета в сочетании с тройным двоеточием перед именем скрытой функции).

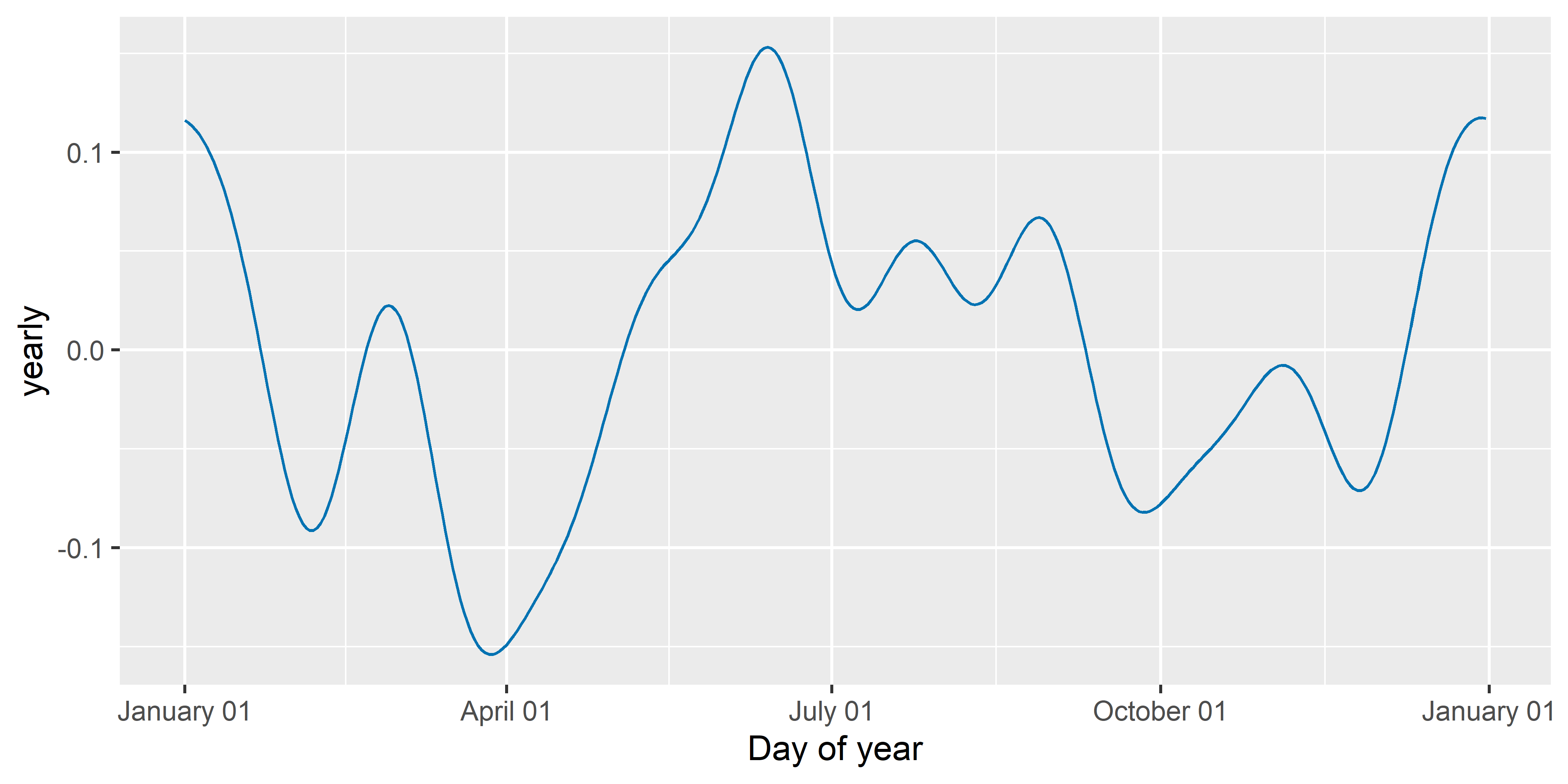
Функция годовой сезонности, оцененная с помощью модели M3

РИСУНОК 6.16: Функция годовой сезонности, оцененная с помощью модели M3

Увеличив значение аргумента yearly.seasonality с заданного по умолчанию 10 до 20, мы получим менее гладкую кривую (рис. 6.17):

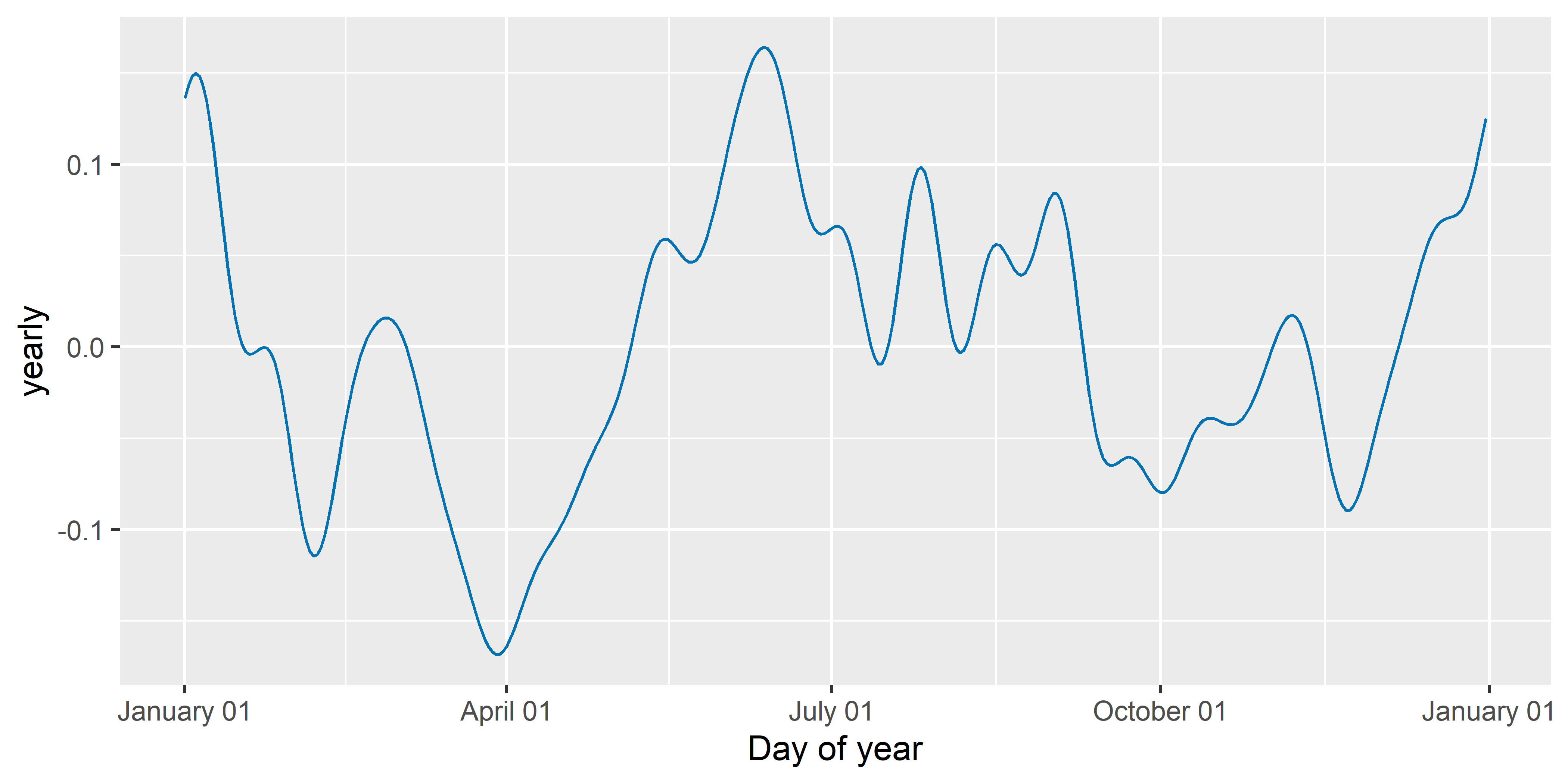
Функция годовой сезонности, оцененная с помощью модели M3B

РИСУНОК 6.17: Функция годовой сезонности, оцененная с помощью модели M3B

6.6.2 Пользовательские сезонные компоненты

Для данных, охватывающих как минимум два года, функция prophet() автоматически добавит в модель компоненты годовой и недельной сезонности. Если гранулярность данных превышает дневную (например, когда имеются почасовые наблюдения зависимой переменной), то в модель автоматически будет добавлена также и компонента дневной сезонности. Помимо этого, пользователи имеют возможность добавить и любые другие сезонные компоненты с помощью функции add_seasonality() (например, часовую, месячную, квартальную и т.п.). Эта функция имеет следующие аргументы:

  • m — модельный объект;
  • name — название сезонной компоненты;
  • period — число (необязательно целое), соответствующее количеству временных интервалов в одном сезонном цикле;
  • fourier.order — порядок (количество членов) ряда Фурье (по умолчанию равен 3 для недельной сезонности и 10 для годовой);
  • mode — тип модели; принимает два возможных значения — "additive" (аддитивная; выбирается по умолчанию) и "multiplicative" (мультипликативная);
  • condition.name — название сторонней переменной, которая задает разные режимы моделируемой сезонности (см. ниже).

Рассмотрим примеры использования функции add_seasonality() и ее аргументов.

В приведенном ниже коде мы сначала отключаем автоматически добавляемую в модель недельную сезонность и вместо нее добавляем месячную (допустив, что один месячный период составляет 30.5 дней). На рис. 6.18 представлены все сезонные компоненты полученной модели (тренд, годовая сезонность и месячная сезонность).

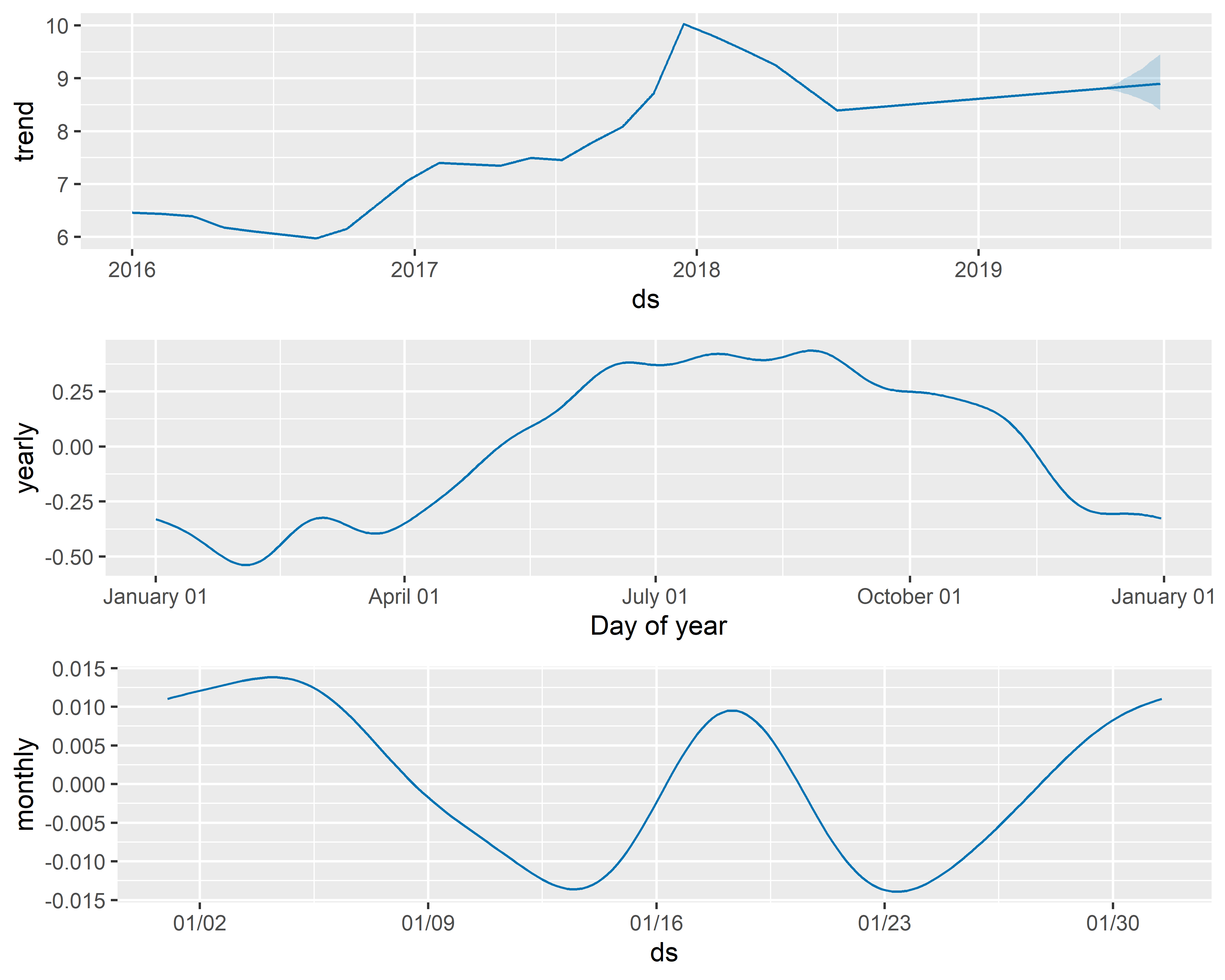
Компоненты модели M10

РИСУНОК 6.18: Компоненты модели M10

Аналогичным образом вместо компоненты месячных колебаний мы могли бы добавить, например, компоненту квартальной сезонности (задав период длиной 365.25/4 дней):

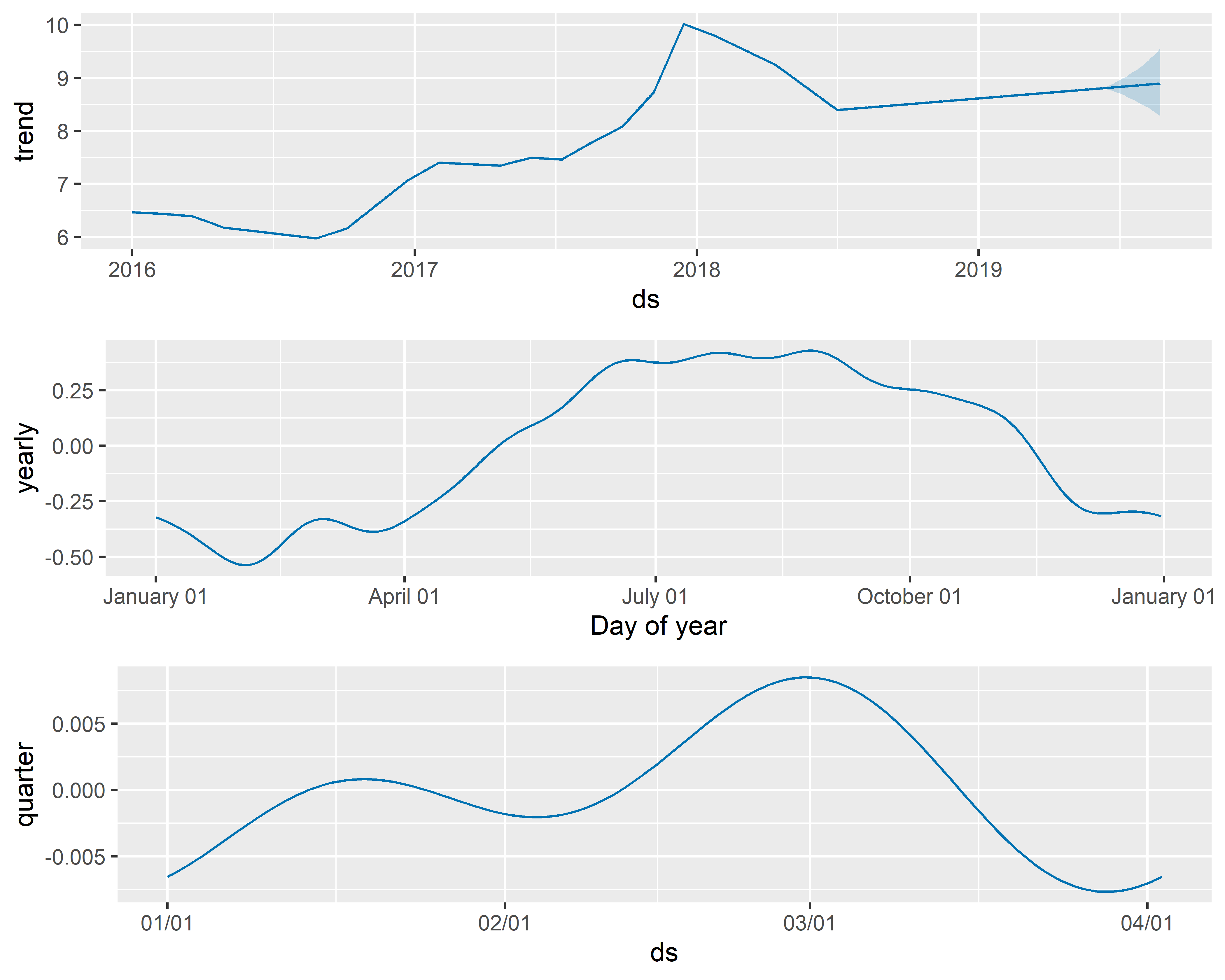
Компоненты модели M11

РИСУНОК 6.19: Компоненты модели M11

6.6.3 Условные режимы сезонности

В ряде случаев функция, аппроксимирующая ту или иную сезонную составляющую, может изменять свои свойства в зависимости от каких–то сторонних факторов. Например, колебания в течение рабочих дней могут иметь характер, сильно отличающийся от такового в выходные дни. Пакет prophet позволяет моделировать такие условные режимы сезонности (т.е. режимы, которые зависят от сторонних факторов) с помощью аргумента condition.name функции add_seasonality(). Как следует из названия, на этот аргумент подается имя (булевой) переменной, которая определяет соответствующий режим. Такие переменные должны хранится в той же таблице, что и основные данные по временному ряду.

Исключительно в качестве примера предположим, что недельные колебания стоимости биткоина в летние месяцы отличаются от таковых в другие месяцы. Чтобы смоделировать такое различие добавим в таблицу с данными bitcoin_train две новые индикаторные переменные: summer (принимает значение TRUE в летние месяцы и FALSE в другие месяцы) и not_summer (TRUE в нелетние месяцы и FALSE летом). Важно помнить, что такие же переменные нужно добавить и в таблицу с будущими датами future_df — иначе прогнозные значения рассчитать не получится:

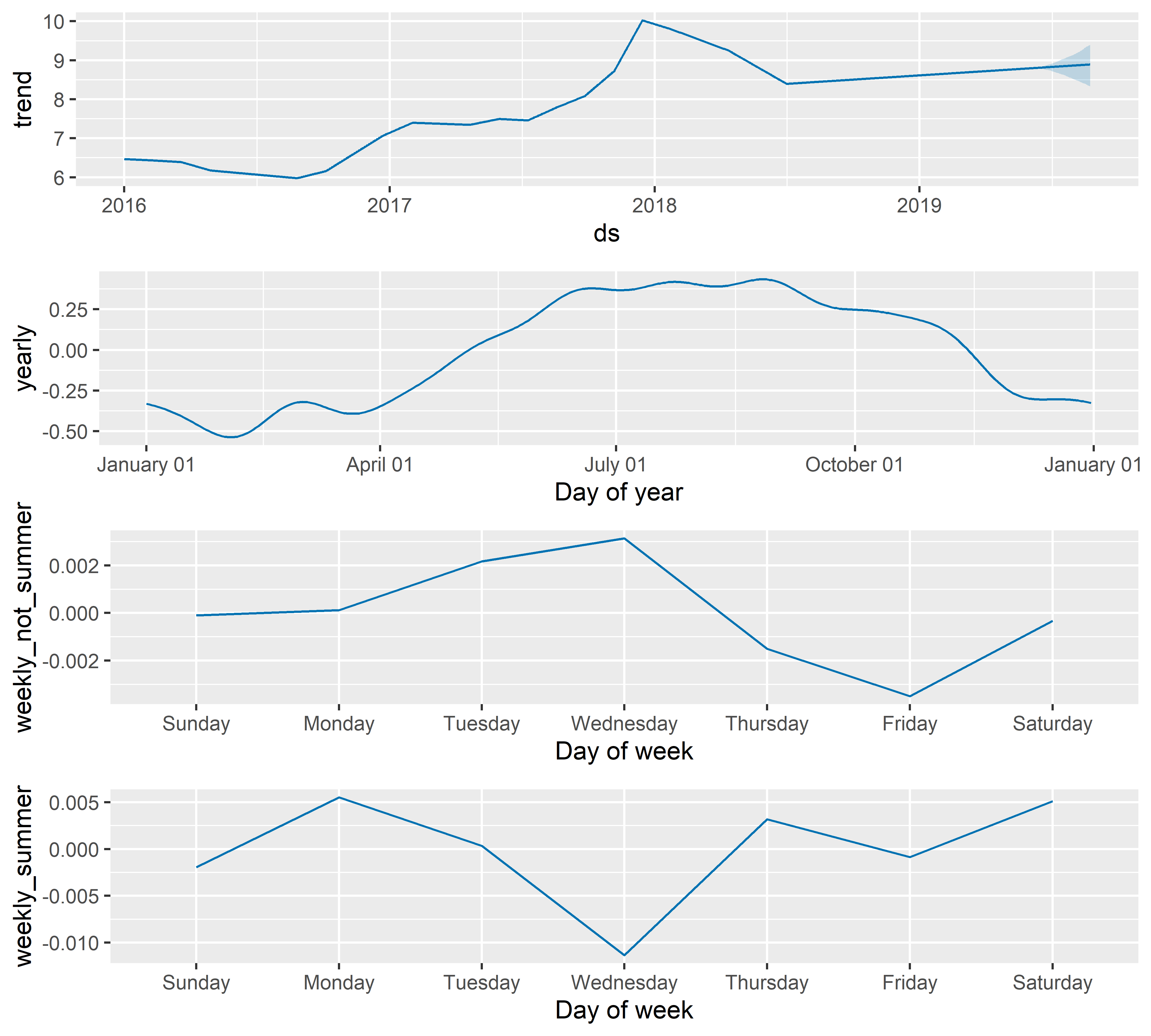
Оцененные компоненты модели M12

РИСУНОК 6.20: Оцененные компоненты модели M12

Согласно полученной модели, в нелетние месяцы стоимость биткоина в течение недели обычно достигает максимума по средам, тогда как в летние месяцы по средам обычно наблюдается противоположная картина (рис. 6.20).

6.6.4 Регуляризация сезонных компонент

Подобно тому, как это было с эффектами праздников и других важных событий (разд. 6.5), мы можем контролировать уровень вклада сезонных компонент. Глобальный контроль выполняется с помощью аргумента seasonality.prior.scale функции prophet() (разд. 6.3). Контроль на уровне отдельных сезонных компонент возможен с помощью аргумента prior.scale функции add_seasonality(). По умолчанию prior.scale = 10. Уменьшение этого значения приведет к подавлению вклада соответствующей компоненты.

6.6.5 Аддитивная и мультипликативная сезонности

Как было отмечено в разд. 1.3, по характеру функциональной связи между своими компонентами модели временных рядов делятся на два основных типа — аддитивные и мультипликативные. Первый из них применяется в случаях, когда амплитуда сезонных колебаний приблизительно постоянна. Если же эта амплитуда заметно изменяется во времени (обычно возрастает), то строят мультипликативную модель.

В пакете prophet по умолчанию подгоняются аддитивные модели временных рядов (разд. 6.1). В мультипликативных моделях, как следует из их названия, сезонная компонента умножается на тренд (в связи с этим вклад сезонных колебаний моделируется в виде доли (%) от уровня тренда):

\[y(t) = g(t) \times s(t) + h(t) + \epsilon_t.\]

В приведенном уравнении предполагается, что амплитуда всех сезонных компонент существенно изменяется во времени. Для подгонки соответствующих моделей необходимо воспользоваться аргументом seasonality.mode функции prophet() (рис. 6.21):

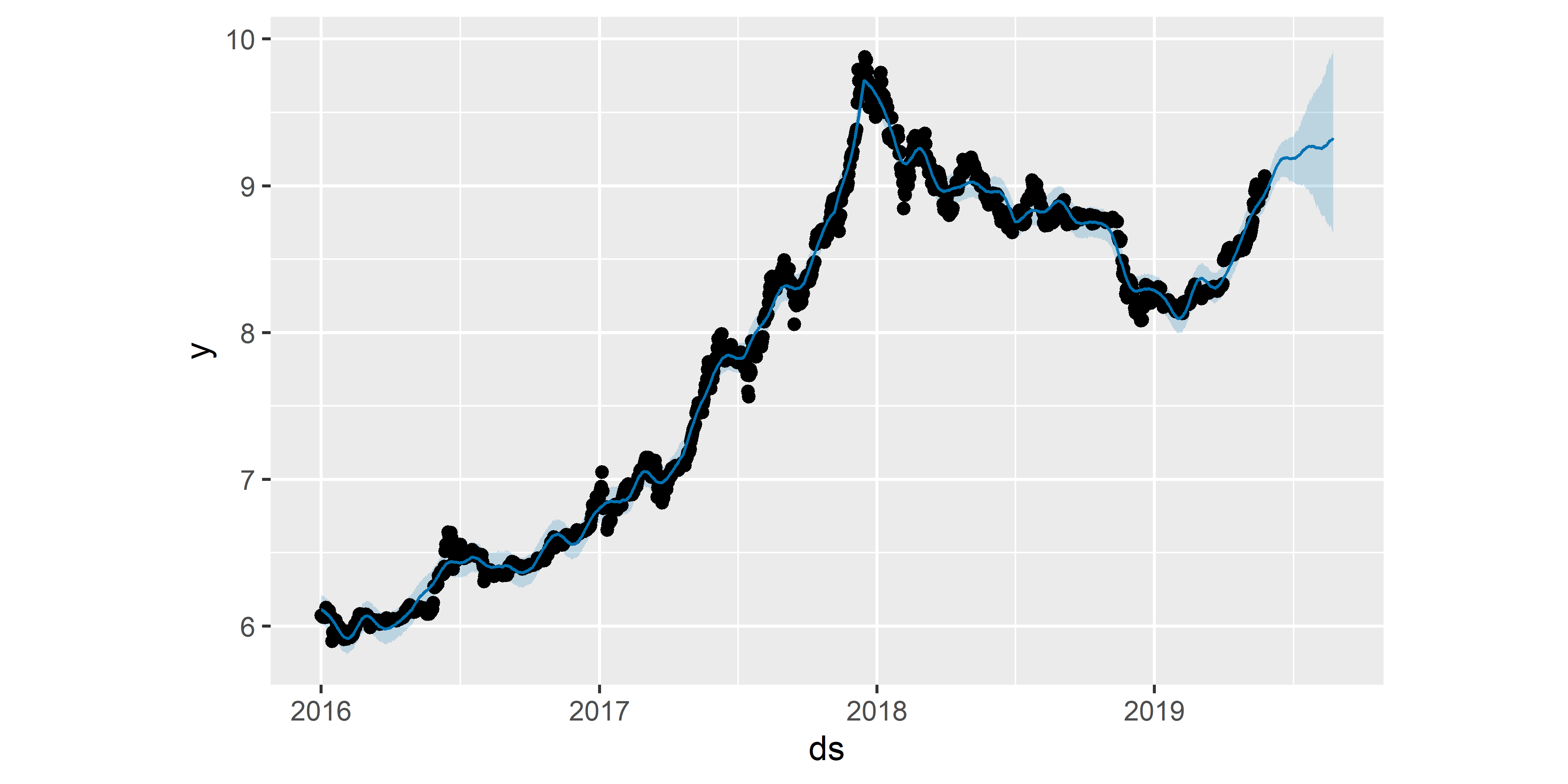
Прогноз стоимости биткоина, полученный на основе модели M14

РИСУНОК 6.21: Прогноз стоимости биткоина, полученный на основе модели M14

Однако в пакете prophet имеется возможность и более тонкого контроля над аддитивностью сезонных компонент. Так, например, можно построить модели, в которых недельная колебания представлены в аддитивном виде, а годовые — в мультипликативном. Вероятно, вы уже догадались, что для этого применяется функция add_seasonality():

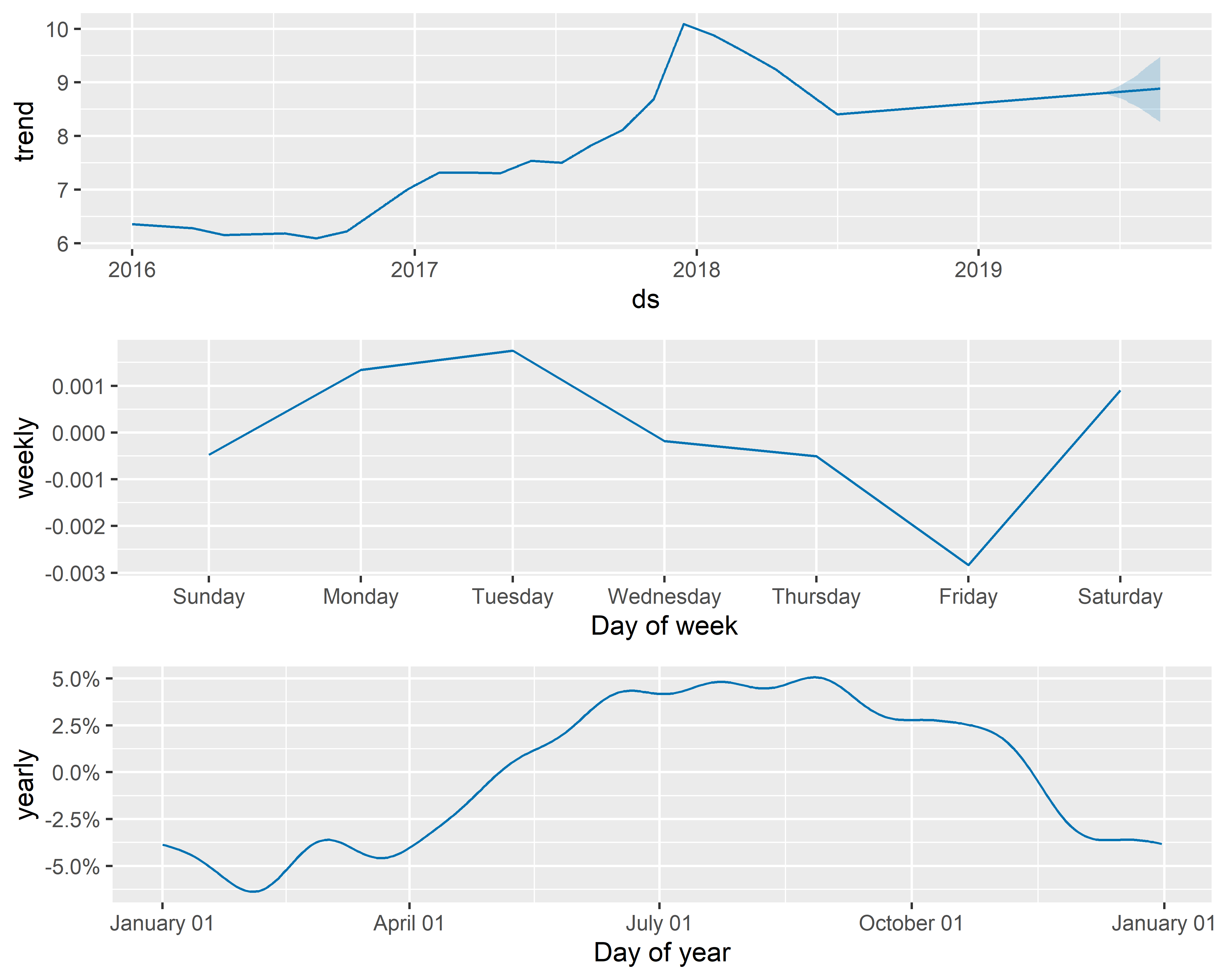
Оцененные компоненты модели M15

РИСУНОК 6.22: Оцененные компоненты модели M15

6.7 Модели с предикторами

Поскольку модели временных рядов, построенные с помощью пакета prophet, представляют собой одну из разновидностей регрессионных моделей (разд. 6.1), то помимо обычных компонент и эффектов “праздников” в такие модели можно добавить и любые другие предикторы. Для этого служит функция add_regressor(), которая имеет следующие аргументы:

  • m — модельный объект;
  • name — название добавляемого предиктора;
  • prior.scale — параметр, используемый для регуляризации эффекта добавляемого предиктора (здесь не рассматривается, однако см., например, разд. 6.5);
  • standardize — позволяет стандартизовать значения добавляемого предиктора перед подгонкой модели (по умолчанию принимает значение "auto" — в этом случае предиктор будет стандартизован, если только он не является индикаторной переменной со значениями 1 и 0; другие возможные значения этого аргумента: TRUE и FALSE);
  • mode — необязательный параметр, определяющий характер сезонности добавляемого предиктора (по умолчанию равен m$seasonality.mode).

Все предикторы, добавляемые в модель с помощью функции add_regressor(), должны присутствовать в таблице с обучающими данными. Для расчета предсказаний будущие значения каждого предиктора должны присутствовать также в таблице с датами, задающими прогнозный отрезок времени. Последнее обстоятельство делает расчет прогноза с использованием количественных предикторов и многих качественных переменных проблематичным: будущие значения таких предикторов (в отличие, например, от дат официальных праздников и других регулярных событий) обычно исследователю не известны. Как правило, для решения этой проблемы сначала строят отдельные модели временных рядов для каждого предиктора, а затем используют предсказанные с помощью таких моделей будущие значения предикторов для получения искомого прогноза. Конечно, такой подход существенно усложняет весь процесс моделирования (поскольку возникает необходимость построения надежных моделей для отдельных предикторов) и потенциально увеличивает неточность прогноза, однако в большинстве случаев это — лучшее, что можно сделать. Именно такой стратегией мы воспользуемся в описанном ниже примере.

Добавим в модель стоимости биткоина три предиктора: цены на акции компаний Amazon, Google и Facebook, хранящиеся в таблице shares_na_filled (гл. 2). Нужно подчеркнуть, что выбор цен на акции в качестве предикторов, равно как и выбор именно этих компаний, ни с чем не связаны — просто такие данные легко получить из публично доступных источников. Добавим эти данные в таблицу bitcoin_train:

## [1] "2016-01-01" "2019-05-26"
## [1] "2016-01-01" "2019-05-26"

Обратите внимание: даты в обеих объединенных нами таблицах лежат в пределах от 2016-01-01 до 2019-05-26 (включительно), что соответствует периоду обучающих данных. Важно также понимать, что на момент написания этого раздела (октябрь 2019 г.) интересующий нас прогнозный период (c 2019-05-27 по 2019-08-24) уже стал историей и, соответственно, цены на акции для этого периода были известны. Но, конечно же, мы не можем использовать эти ставшие историей данные для прогнозирования стоимости биткоина на период с 2019-05-27 по 2019-08-24: в реальной ситуации при расчете прогноза подобное “заглядывание в будущее” было бы невозможно.

Следует также отметить, что хотя prophet–модели мало чувствительны к наличию пропущенных значений в зависимой переменной, пропущенные значения в предикторах недопустимы. Поэтому в приведенном выше коде мы добавили в исходные данные таблицу shares_na_filled, в которой пропущенные наблюдения уже были восстановлены (методом LOCF, см. гл. 2).

Как отмечено выше, цены на акции Amazon, Google и Facebook выбраны в качестве предикторов исключительно из удобства. Тем не менее, все три переменные демонстрируют определенную (нелинейную) связь со стоимостью биткоина и, соответственно, вполне подходят для наших целей (рис. 6.23):

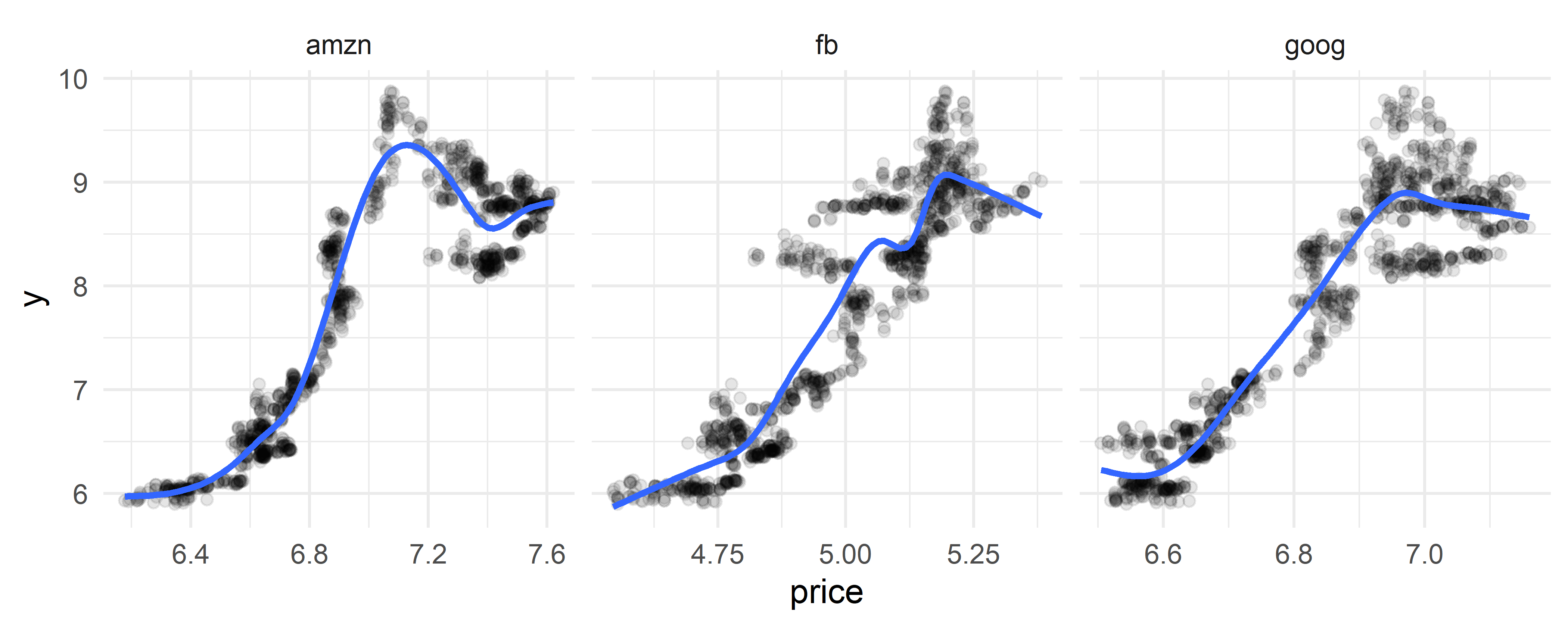
Связь между ценой акций трех компаний и стоимостью биткоина

РИСУНОК 6.23: Связь между ценой акций трех компаний и стоимостью биткоина

Однако прежде, чем перейти к построению модели стоимости биткоина, нам необходимо решить проблему с будущими значениями предикторов. Для этого мы построим отдельные модели для каждого предиктора, а затем рассчитаем их предсказанные значения для интересующего нас прогнозного периода:

## # A tibble: 6 x 4
##   ds                   amzn    fb  goog
##   <dttm>              <dbl> <dbl> <dbl>
## 1 2016-01-01 00:00:00  6.34  4.55  6.55
## 2 2016-01-02 00:00:00  6.35  4.55  6.55
## 3 2016-01-03 00:00:00  6.35  4.55  6.55
## 4 2016-01-04 00:00:00  6.35  4.55  6.56
## 5 2016-01-05 00:00:00  6.36  4.55  6.56
## 6 2016-01-06 00:00:00  6.36  4.56  6.56

Исходные данные и прогнозные значения цен на акции показаны на рис. 6.24.

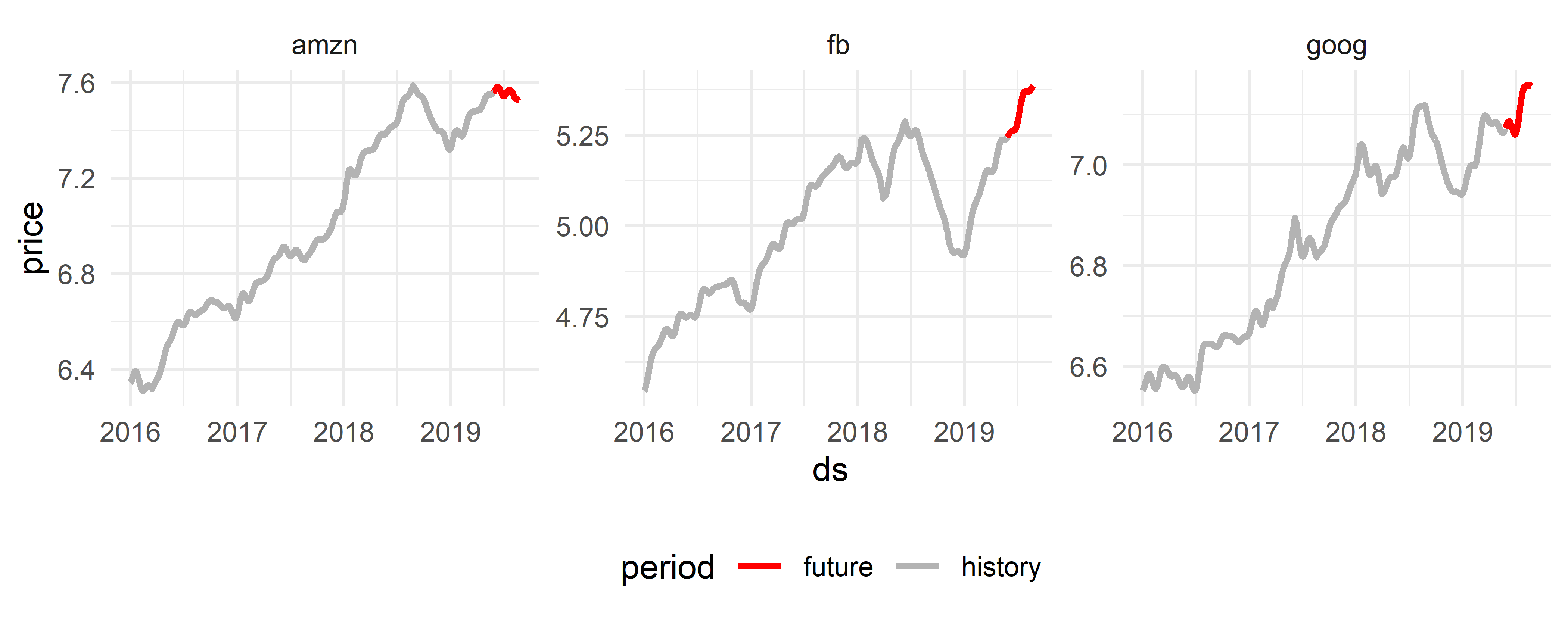
Исторические данные по цене акций (серые линии) и предсказанные значения (красные линии)

РИСУНОК 6.24: Исторические данные по цене акций (серые линии) и предсказанные значения (красные линии)

Теперь у нас есть все, чтобы построить модель стоимости биткоина с тремя предикторами и рассчитать прогнозные значения (рис. 6.25):

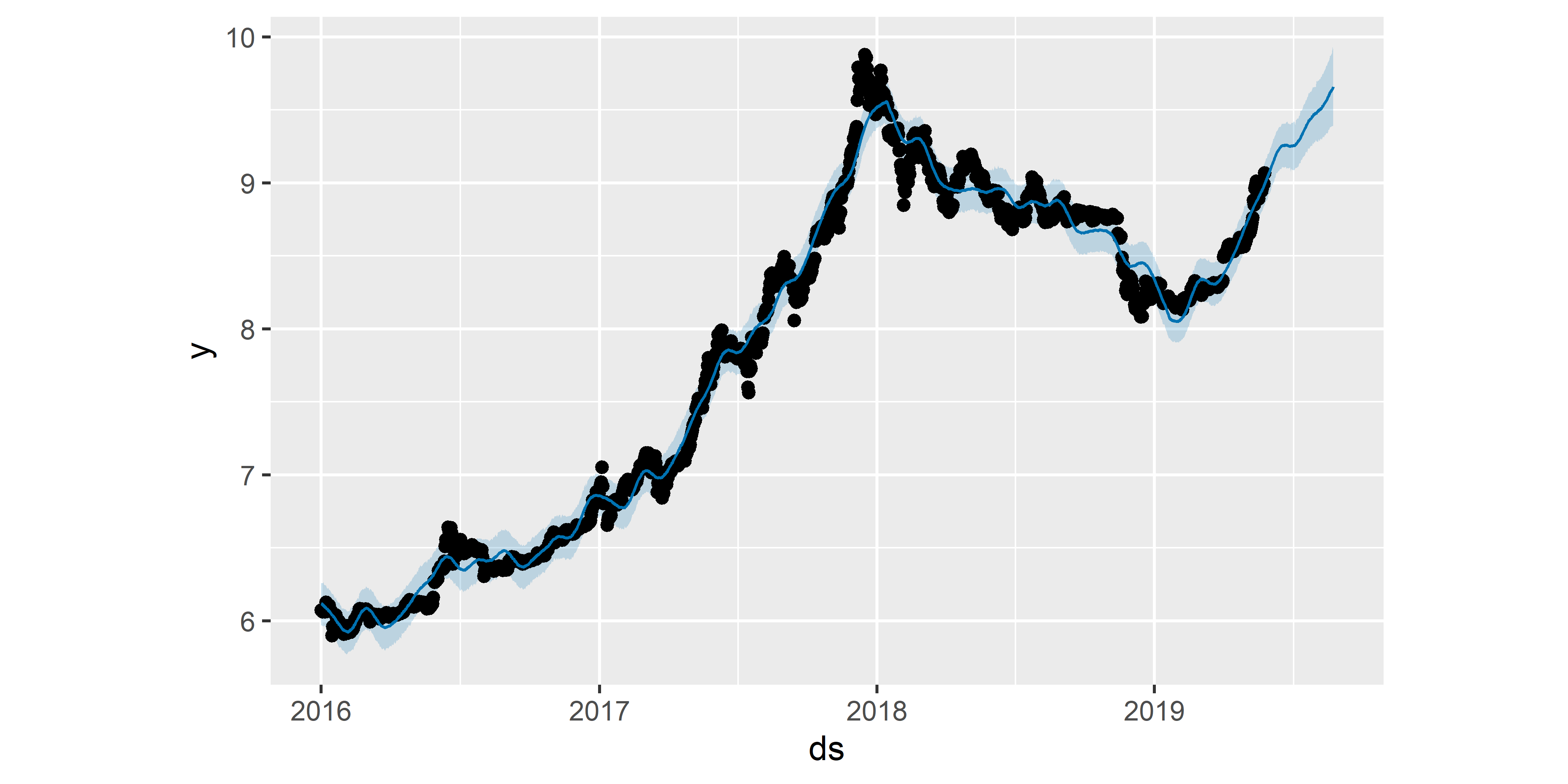
Прогноз стоимости биткоина, полученный на основе модели M16

РИСУНОК 6.25: Прогноз стоимости биткоина, полученный на основе модели M16

На рис. 6.26 представлены оцененные компоненты модели M16. Заметьте, что эффекты всех трех предикторов объединены в одну компоненту (см. extra_regressors_additive на графике внизу):

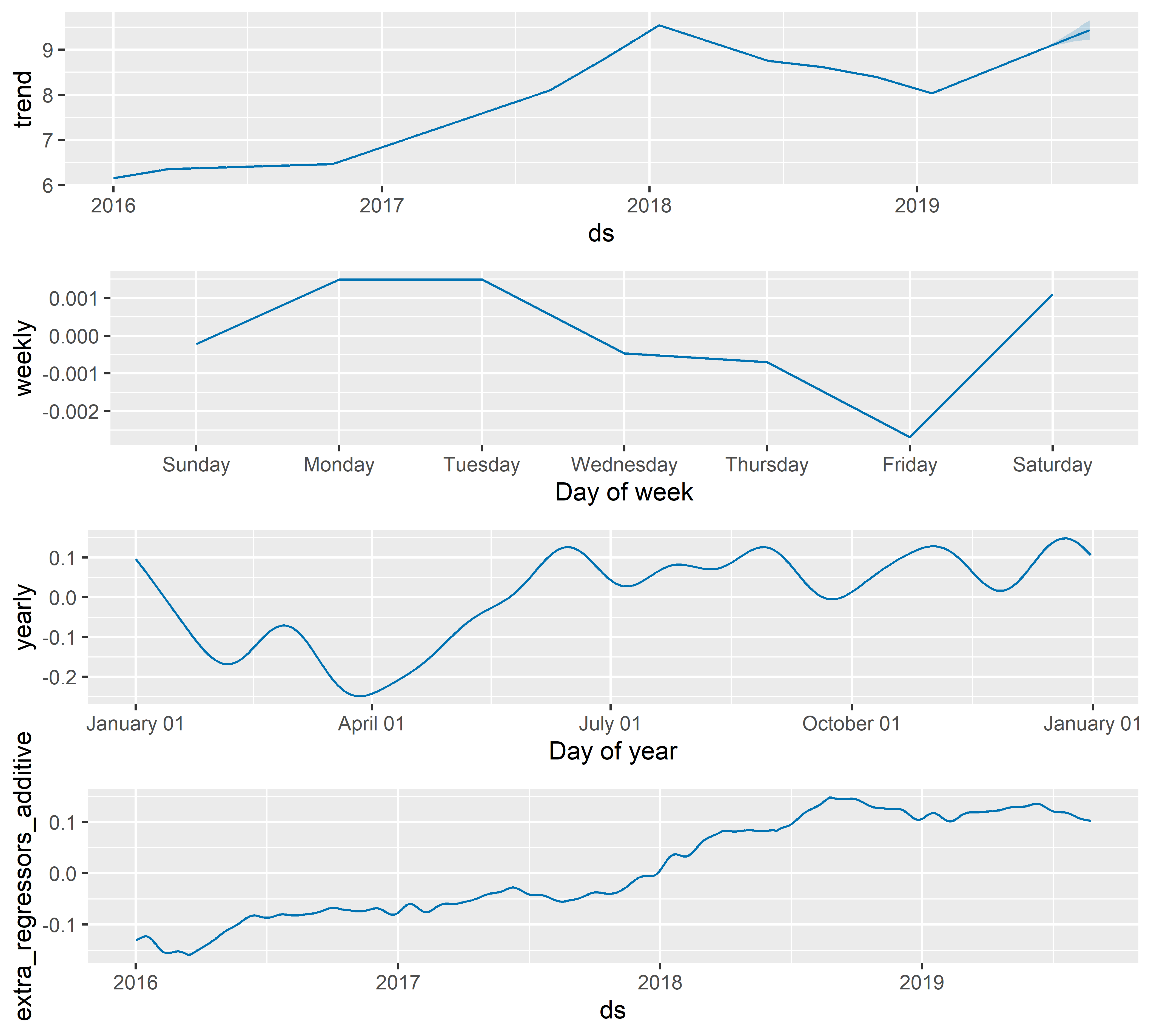
Оцененные компоненты модели M16

РИСУНОК 6.26: Оцененные компоненты модели M16

С помощью рассмотренной ранее функции plot_forecast_component() (разд. 6.5) мы можем также изобразить эффекты отдельных предикторов (рис. 6.27):

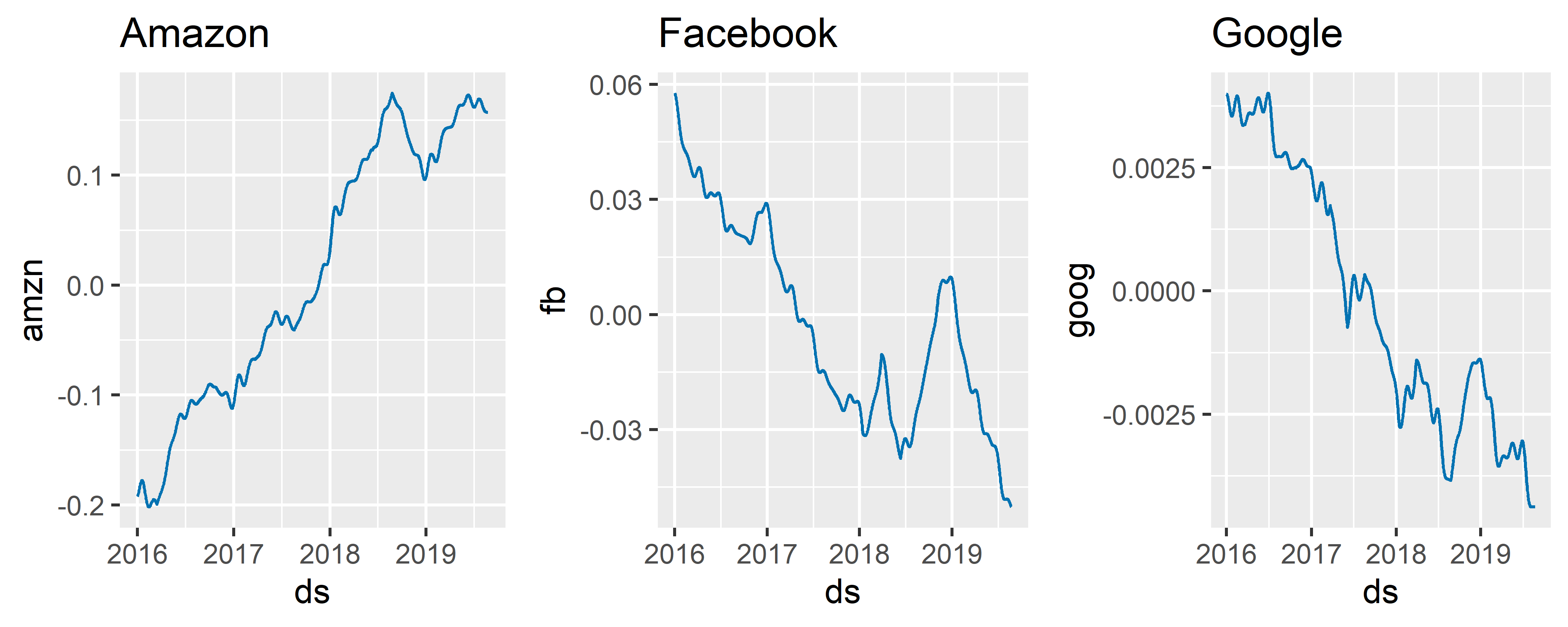
Оцененные эффекты предикторов, включенных в модель M16

РИСУНОК 6.27: Оцененные эффекты предикторов, включенных в модель M16

Согласно полученной модели, эффект переменной amzn оказался сильнее (примерный диапазон значений от –0.2 до 0.2), чем эффекты goog (от –0.005 до 0.005) и fb (от –0.06 до 0.06). Мы можем сделать такое заключение благодаря тому, что эффекты всех трех предикторов представлены на одной шкале и поэтому сравнимы (значения всех этих переменных перед подгонкой модели были стандартизованы — см. выше описание аргумента standardize функции add_regressor()). Интересно также, что характер изменения эффекта amzn во времени почти зеркально отличается от такового у переменных goog и fb. Оставим читателям возможность подумать над интерпретацией этого наблюдения самостоятельно.

В рассмотренном нами примере все добавленные в модель независимые переменные были количественными. В случае с качественными предикторами у исследователя есть два варианта на выбор: либо представить значения таких переменных в виде “праздников” (разд. 6.5), либо воспользоваться описанной выше более общей функцией add_regressor(). В обоих случаях качественные переменные необходимо преобразовать в индикаторные (т.е. создать отдельные столбцы для каждого уровня переменной со значениями 1 и 0).

6.8 Выбор оптимальной модели

В предыдущих разделах этой главы мы построили целый ряд моделей для прогнозирования стоимости биткоина. Но какая из этих моделей лучше? Стандартным методом оценки качества нескольких альтернативных моделей является перекрестная проверка. Суть этого метода сводится к тому, что исходные обучающие данные случайным образом разбиваются на \(K\) частей (блоков), после чего модель \(k\) раз подгоняется по \(K - 1\) блокам, а оставшийся блок каждый раз используется для проверки качества предсказаний на основе той или иной подходящей случаю метрики. Полученная таким образом средняя метрика будет хорошей оценкой качества предсказаний модели на новых данных.

К сожалению, в случае с моделями временных рядов такой способ выполнения перекрестной проверки не имеет смысла и не отвечает стоящей задаче. Поскольку во временных рядах, как правило, имеет место значительная автокорреляция (гл. 4), то мы не можем просто разбить такой ряд случайным образом на \(K\) частей — это приведет к потере указанной корреляции. Более того, в результате случайного разбиения данных на несколько блоков может получиться так, что в какой–то из итераций мы построим модель преимущественно по недавним наблюдениям, а затем оценим ее качество на блоке из давних наблюдений. Другими словами, мы построим модель, которая будет предсказывать прошлое, что не имеет никакого смысла — ведь мы пытаемся решить задачу по предсказанию будущего!

Для решения описанной проблемы при работе с временными рядами применяют несколько модификаций перекрестной проверки (Hyndman and Athanasopoulos 2019; Tashman 2000). В пакете prophet, в частности, реализован т.н. метод “имитированных исторических прогнозов” (Simulated Historical Forecasts, SHF). Рассмотрим, что этот метод собой представляет, и как им пользоваться для выбора оптимальной модели.

6.8.1 Метод имитированных исторических прогнозов

Любая модель временного ряда строится на основе данных, собранных в течение некоторого периода в прошлом. Далее по полученной модели рассчитываются прогнозные значения для интересующего нас промежутка времени (горизонта) в будущем. Такая процедура повторяется каждый раз, когда необходимо сделать новый прогноз (рис. 6.28).

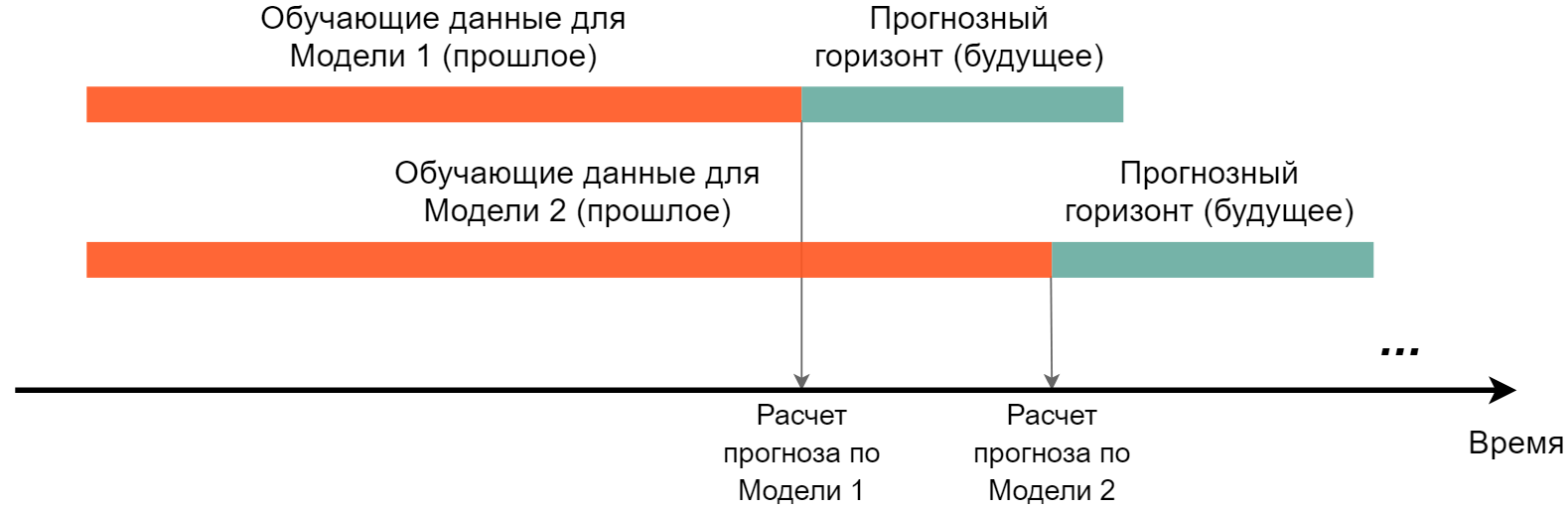
Стандартная процедура построения моделей для прогнозирования временных рядов

РИСУНОК 6.28: Стандартная процедура построения моделей для прогнозирования временных рядов

Метод SHF (рис. 6.29) пытается сымитировать описанную выше процедуру. В пределах отрезка с исходными обучающими данными выбирают \(K\) “точек отсчета” (“cut–off points” по терминологии prophet), на основе которых формируются блоки данных для выполнения перекрестной проверки: все исторические наблюдения, предшествующие \(k\)–й точке отсчета (а также сама эта точка), образуют обучающие данные для подгонки соответствующей модели, а \(H\) исторических наблюдений, следующих за точкой отсчета, образуют прогнозный горизонт. Расстояние между точками отсчета называется “периодом” (“period”) и по умолчанию составляет \(H / 2\). Обучающие наблюдения в первом из \(K\) блоков образуют т.н. “initial period” (“начальный отрезок”). В prophet длина этого отрезка по умолчанию составляет \(3 \times H\), однако исследователь при желании может ее изменить.

Каждый раз после подгонки модели на обучающих данных из \(k\)–го блока рассчитываются предсказания для прогнозного горизонта того же блока, что позволяет оценить качество прогноза с помощью подходящей случаю метрики (например, RMSE; см. ниже). Значения этой метрики, усредненные по каждой дате прогнозных горизонтов каждого блока, в итоге дают оценку качества предсказаний, которую можно ожидать от модели, построенной по всем исходным обучающим данным. Это в свою очередь позволяет сравнить несколько альтернативных моделей и выбрать оптимальную.

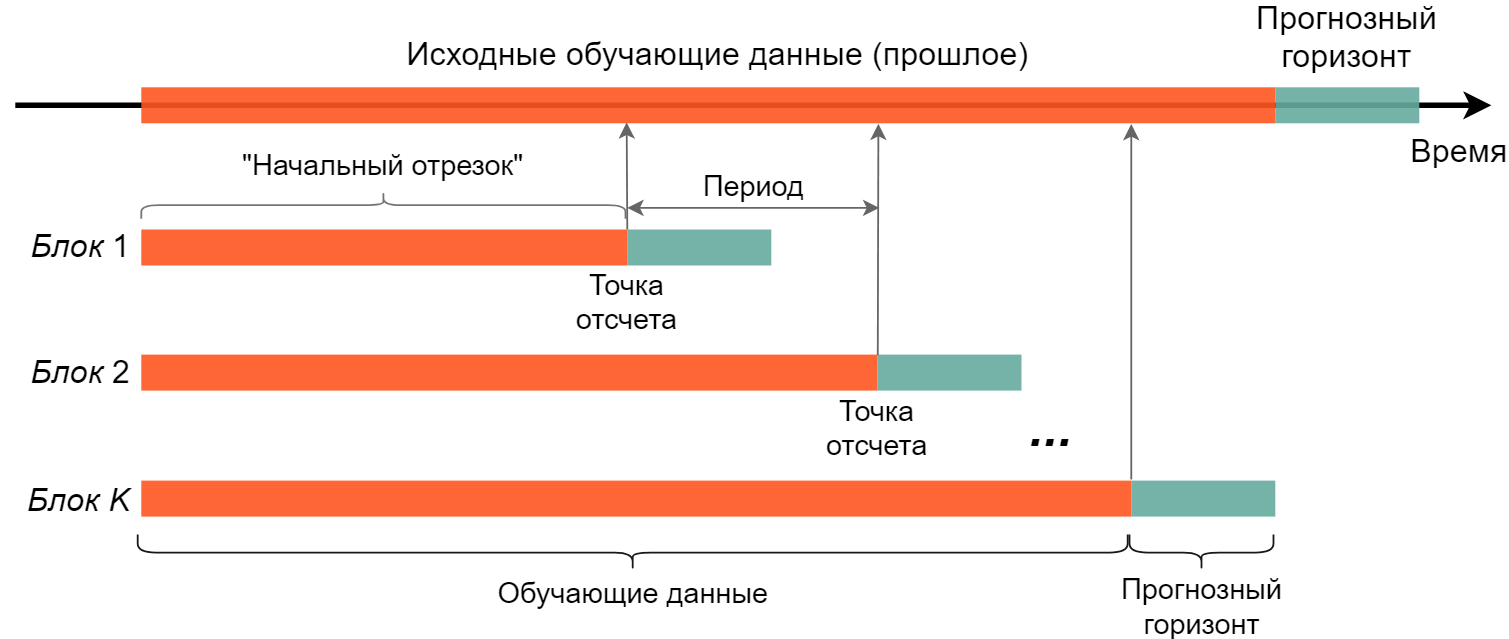
Процедура, лежащая в основе метода имитированных исторических прогнозов

РИСУНОК 6.29: Процедура, лежащая в основе метода имитированных исторических прогнозов

Таким образом, SHF близок к классическому способу выполнения перекрестной проверки моделей временных рядов по методу “скользящей точки отсчета” (“rolling origin evaluation”; Tashman 2000), однако отличается от последнего тем, что для оценивания качества предсказаний используется меньше блоков и прогнозные горизонты этих блоков удалены друг от друга на некоторое расстояние. С одной стороны, это является преимуществом метода SHF, поскольку он требует меньше вычислений и получаемые оценки качества предсказаний не так сильно коррелируют друг с другом, как в случае с перекрестной проверкой по методу “скользящей точки отсчета”. С другой стороны, при небольшом количестве блоков \(K\) оценка качества модели может оказаться ненадежной. С решением последней проблемы отчасти помогает увеличение отрезка исходных исторических данных (поскольку чем он длиннее, тем больше блоков можно в него вместить). Однако следует помнить, что модели, построенные на длинных временных рядах, часто демонстрируют низкое качество прогнозов, поскольку параметры таких моделей задать труднее и возрастает риск переобучения.

6.8.2 Выполнение перекрестной проверки

В пакете prophet перекрестная проверка по методу имитированных исторических прогнозов выполняется с помощью функции cross_validation(), которая имеет следующие аргументы:

  • model — модельный объект;
  • horizon — длина прогнозного горизонта в каждом блоке данных, используемом для выполнения перекрестной проверки;
  • units — название единицы измерения времени (например, "days", "hours", "secs" — см. справочный файл по базовой функции difftime());
  • initial — длина начального отрезка с обучающими данными в первом блоке.

Функция cross_validation() возвращает таблицу c наблюденными (y) и оцененными (yhat) значениями моделируемой переменной, а также доверительными границами предсказанных значений (yhat_lower и yhat_upper) для каждой точки отсчета cutoff и каждой даты ds соответствующего прогнозного периода (в примере используется модель M3 из разд. 6.4):

##          y         ds     yhat yhat_lower yhat_upper     cutoff
## 1 9.349206 2018-03-03 9.226595   9.113810   9.338773 2018-03-02
## 2 9.351197 2018-03-04 9.212202   9.108078   9.321019 2018-03-02
## 3 9.356456 2018-03-05 9.206319   9.096260   9.311673 2018-03-02
## 4 9.285439 2018-03-06 9.193538   9.085362   9.307952 2018-03-02
## 5 9.206891 2018-03-07 9.181843   9.069791   9.287407 2018-03-02
## 6 9.147934 2018-03-08 9.171255   9.056305   9.283333 2018-03-02

6.8.3 Метрики качества модели

Как следует из ее названия, функция performance_metrics() позволяет рассчитать метрики, характеризующие качество предсказаний моделей. В частности, имеется возможность рассчитать следующие показатели:

  • Среднеквадратичная ошибка (mean squared error, MSE):

\[MSE = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2 \]

  • Квадратный корень из среднеквадратичной ошибки (root mean squared error, RMSE):

\[RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2}\]

  • Средняя абсолютная ошибка (mean absolute error, MAE):

\[MAE = \sum_{i=1}^n |y_i - \hat{y}_i| \]

  • Средняя абсолютная удельная ошибка (mean absolute percentage error, MAPE):

\[MAPE = \sum_{i=1}^n |\frac{y_i - \hat{y}_i}{y_i}|\]

  • “Покрытие” (coverage): доля истинных значений моделируемой переменной, которые находятся в пределах доверительных границ прогноза.

В приведенных формулах \(y_i\) и \(\hat{y}_i\) — это истинное и предсказанное значения моделируемой переменной соответственно, а \(n\) — количество наблюдений.

Функция performance_metrics() имеет следующие аргументы:

  • df — таблица, полученная с помощью функции cross_validation();
  • metrics — вектор с названиями метрик качества модели (по умолчанию этот аргумент принимает значение NULL, что приводит к расчету всех перечисленных выше метрик, т.е. c("mse", "rmse", "mae", "mape", "coverage"));
  • rolling_window — размер “скользящего окна”, в пределах которого происходит усреднение каждой метрики (по умолчанию принимает значение 0.1, т.е. 10% от длины прогнозного горизонта; см. пояснения ниже).

На рис. 6.30 представлено схематичное изображение того, как функция performance_metrics() рассчитывает метрики качества модели в случае с перекрестной проверкой по 5 блокам данных с длиной прогнозного горизонта \(H = 100\) и аргументом rolling_window = 0.1.

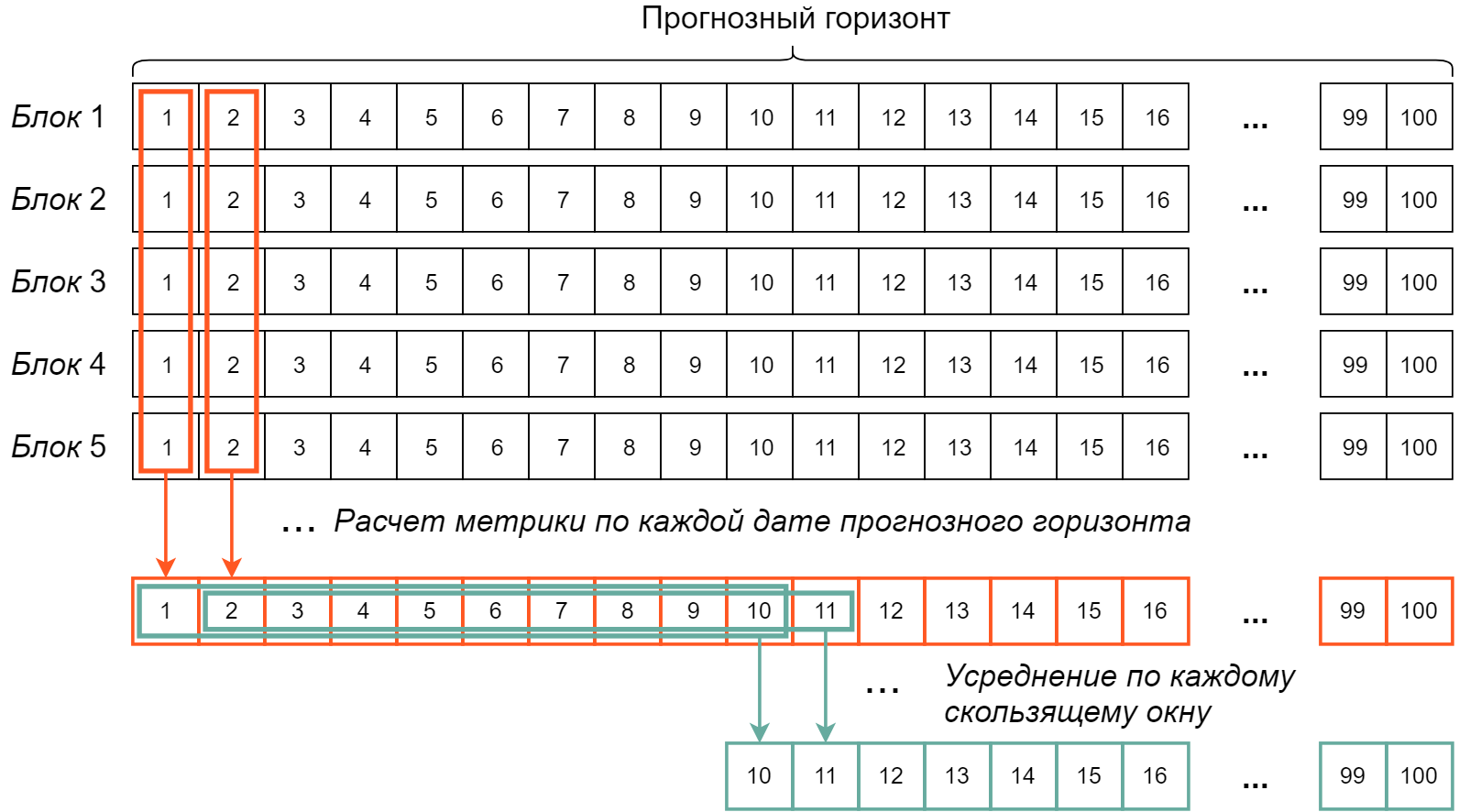
Процедура расчета метрик качества моделей при выполнении перекрестной проверки по методу SHF

РИСУНОК 6.30: Процедура расчета метрик качества моделей при выполнении перекрестной проверки по методу SHF

В приведенном ниже примере функция performance_metrics() применена для расчета среднеквадратичной ошибки прогноза построенной нами ранее модели M3:

##   horizon        mse
## 1  9 days 0.06424673
## 2 10 days 0.07572021
## 3 11 days 0.08695892
## 4 12 days 0.09707747
## 5 13 days 0.10990773
## 6 14 days 0.12260315

Как видно из полученного результата, первое усредненное значение MSE приходится на 9–й день прогнозного горизонта, поскольку длина этого горизонта для модели M3 составляет 90 дней (см. выше код для создания таблицы M3_cv), а 9 — это 10% от этой длины (размер скользящего окна, задаваемый аргументом rolling_window).

Если аргументу rolling_window присвоить значение 0, то запрашиваемые метрики качества будут рассчитаны для каждой даты прогнозного горизонта (т.е. размер скользящего окна в данном случае фактически равен 1):

##   horizon        mse
## 1  1 days 0.03595728
## 2  2 days 0.03941046
## 3  3 days 0.05343681
## 4  4 days 0.05035319
## 5  5 days 0.05454100
## 6  6 days 0.07256616

Если же аргументу rolling_window присвоить значение 1, то запрашиваемые метрики качества будут усреднены по всему прогнозному горизонту:

##   horizon      mse
## 1 90 days 0.192834

Метрики качества моделей, полученные в ходе перекрестной проверки, можно визуализировать с помощью функции plot_cross_validation_metric(), которая имеет следующие аргументы:

  • df_cv — таблица, полученная с помощью функции cross_validation();
  • metric — название метрики;
  • rolling_window — размер “скользящего окна”, в пределах которого происходит усреднение метрики (см. рис. 6.30 и описание функции performance_metrics()).

Функция plot_cross_validation_metric() возвращает объект класса ggplot:

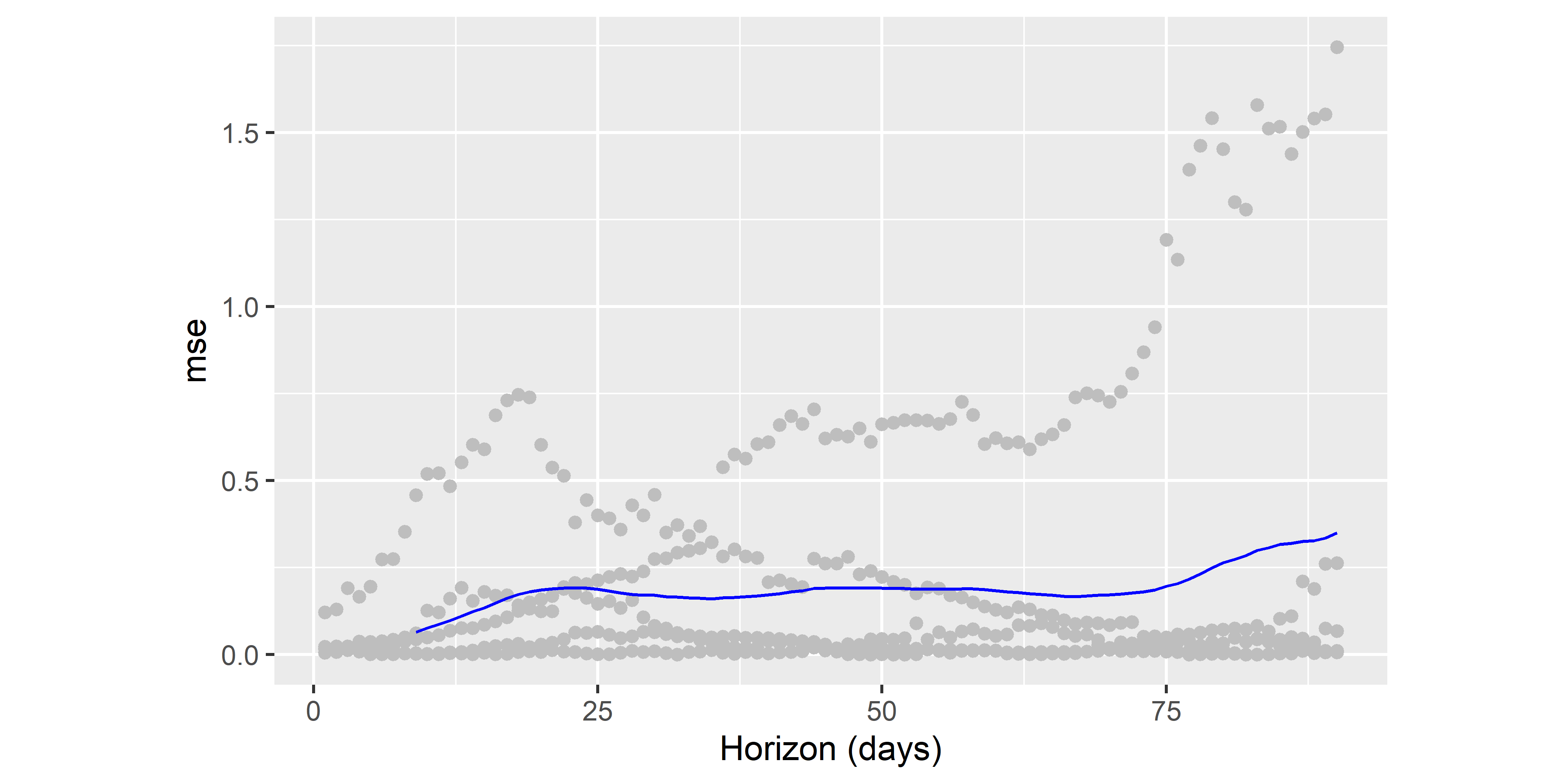
Визуализация метрики качества предсказаний (MSE), полученной по результатам перекрестной проверки модели M3

РИСУНОК 6.31: Визуализация метрики качества предсказаний (MSE), полученной по результатам перекрестной проверки модели M3

На рис. 6.31 приведены оценки MSE для каждой из дат прогнозного горизонта (\(H = 90\)) каждого из \(K = 5\) блоков данных, участвовавших в перекрестной проверке. Голубая линия соответствует усредненным значениям в пределах каждого скользящего окна размером в 9 наблюдений. Судя по большому разбросу полученных оценок MSE, качество модели M3 желает оставлять лучшего.

6.8.4 Пример выбора оптимальной модели

Рассмотрим теперь, как описанную выше методологию выполнения перекрестной проверки можно применить для выбора оптимальной модели из нескольких альтернативных. Предположим, что перед нами стоит задача выбрать оптимальную модель стоимости биткоина из построенных ранее моделей M4, M5 и M12. Для описания качества этих моделей воспользуемся двумя метриками: MAPE и покрытие (подразд. 6.8.3). Для упрощения примера предположим также, что нас интересует качество предсказаний в целом для 90–дневного прогнозного горизонта (т.е. нам неинтересны отдельные даты этого горизонта). Рассчитаем обе метрики качества для каждой из моделей–кандидатов:

##   horizon       mape  coverage
## 1 90 days 0.03214045 0.2851852
##   horizon       mape coverage
## 1 90 days 0.03717749 0.462963
##   horizon       mape coverage
## 1 90 days 0.02347762 0.637037

Как видим, M12 лучше других моделей по обеим выбранным метрикам качества. Это можно видеть также из графиков, построенных с помощью функции plot_cross_validation_metric() (рис. 6.32):

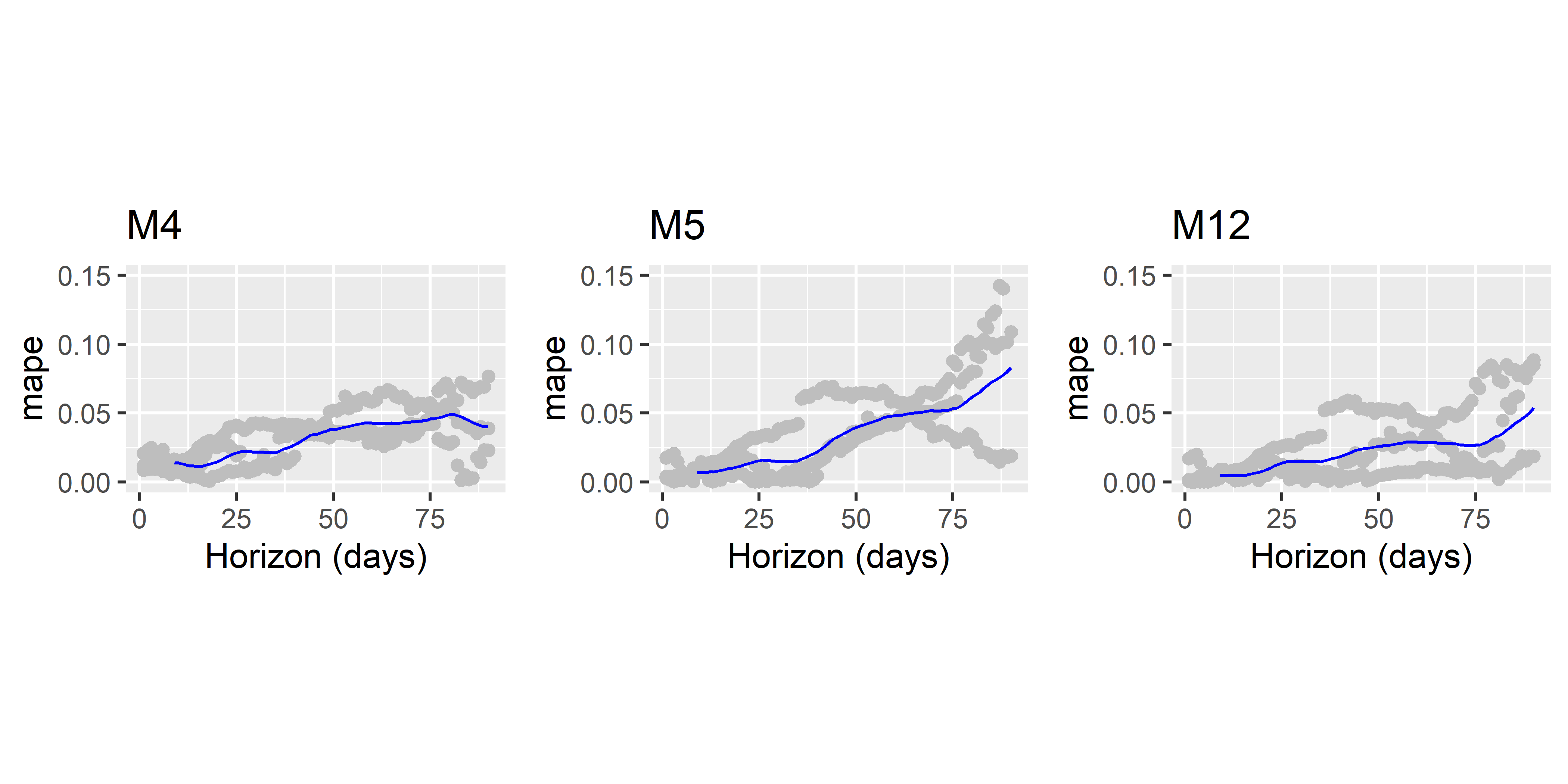
Сравнение качества предсказаний трех моделей по метрике MAPE

РИСУНОК 6.32: Сравнение качества предсказаний трех моделей по метрике MAPE

Вспомним, что до сих пор мы строили все модели по обучающим данным из таблицы bitcoin_train. Однако у нас есть и проверочный набор данных — bitcoin_test (см. разд. 6.2). Посмотрим, как выбранная нами оптимальная модель M12 сработает на этой проверочной выборке. На рис. 6.33 представлены обучающие данные (черные точки; для удобства показаны наблюдения только за 2019 г.) и истинные значения стоимости биткоина в прогнозном периоде (красные точки). Голубая сплошная линия на этом графике соответствует предсказанным моделью значениям, а светло–голубая полоса вокруг нее — 80%–ной доверительной области предсказанных значений:

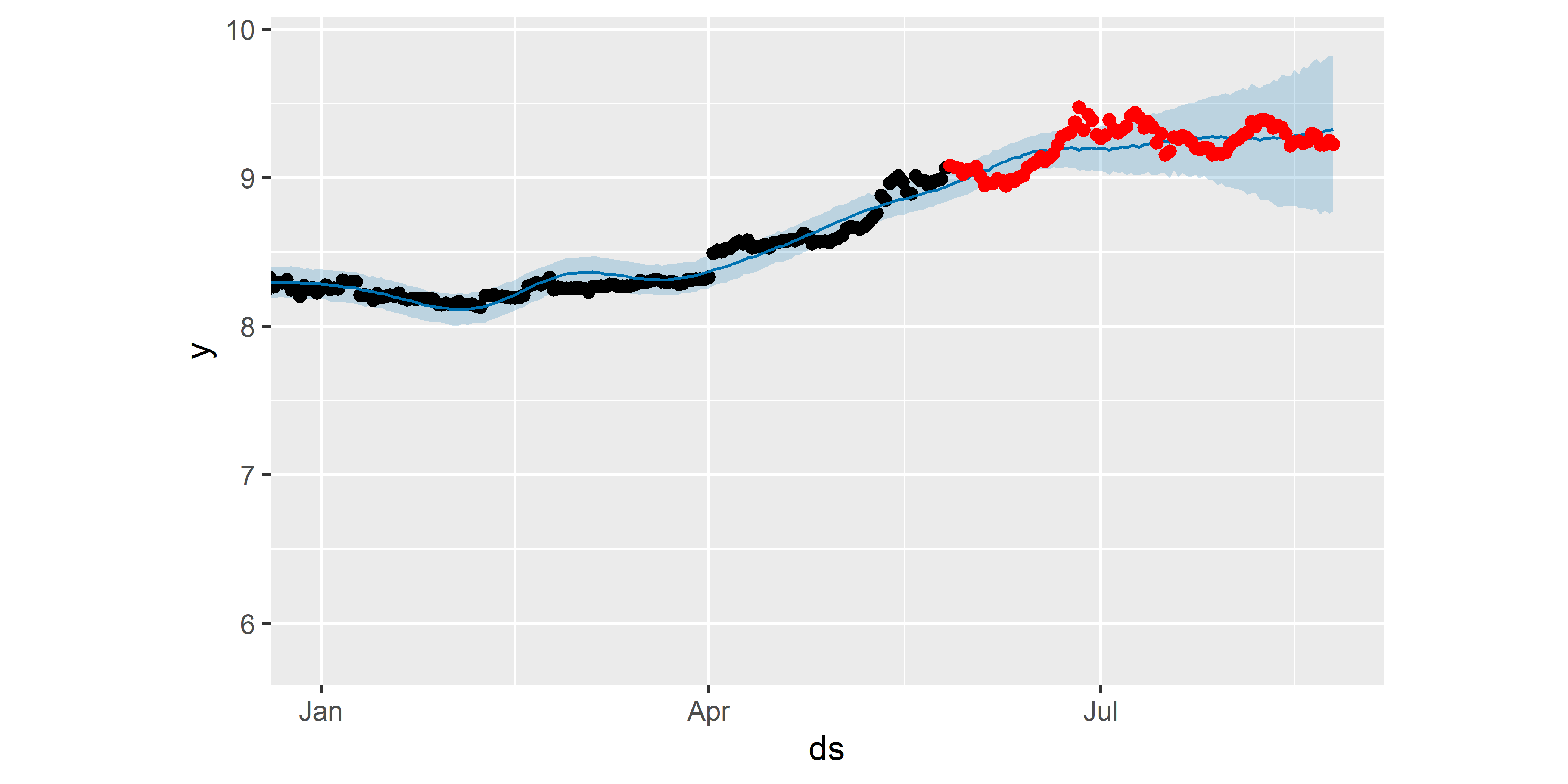
Сравнение истинных значений стоимости биткоина и прогнозных значений, полученных с помощью модели M12. См. пояснения в тексте

РИСУНОК 6.33: Сравнение истинных значений стоимости биткоина и прогнозных значений, полученных с помощью модели M12. См. пояснения в тексте

Хотя выбранная нами в качестве оптимальной модель M12 не смогла правильно предсказать некоторые локальные колебания стоимости биткоина в прогнозном периоде, в целом она дала неплохой результат: большинство истинных значений стоимости оказалось в пределах 80%–ной доверительной полосы. Однако следует подчеркнуть, что это всего лишь пример использования перекрестной проверки для сравнения качества предсказаний нескольких моделей: совершенно точно не стоит разрабатывать стратегию торговли биткоином на основе приведенных здесь результатов!

6.9 Моделирование емкости системы

Во всех примерах из предыдущих разделов этой главы предполагалось, что моделируемая переменная может расти во времени бесконечно. Однако многие системы имеют естественную “емкость”, выше которой рост невозможен. Классическим примером здесь будет численность популяции какого–либо биологического вида, которая ограничена имеющимися в среде обитания ресурсами. Другой пример — количество пользователей какой–либо онлайн–услуги, которое ограничено доступом в Интернет. Важно отметить, что емкость системы может иметь ограничения и по нижнему порогу (например, численность населения не может быть отрицательной). Одной из особенностей пакета prophet является возможность моделировать временные ряды для подобных систем. Рассмотрим, как это происходит.

6.9.1 Тренд с насыщением

Стандартным подходом для описания роста в системе с ограниченной емкостью является использование логистической функции следующего вида: \[g(t) = \frac{C}{1 + \exp(-k(t-m))},\] где \(C\) — это верхний порог (емкость системы), \(k\) — скорость роста, \(t\) — время, а \(m\) — параметр, позволяющий “сдвигать” функцию вдоль оси времени. На рис. 6.34 показаны примеры логистической функции с разными значениями параметров.

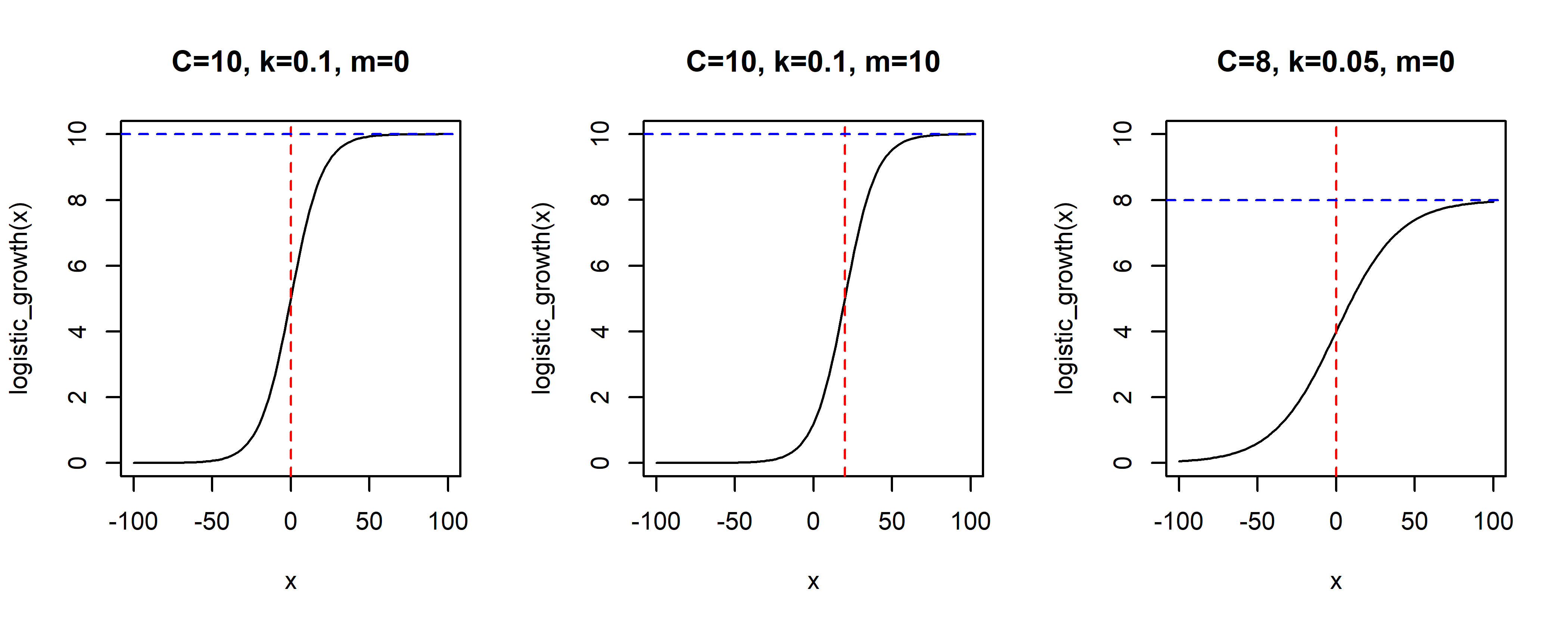
Примеры логистической функции с разными значениями параметров

РИСУНОК 6.34: Примеры логистической функции с разными значениями параметров

Есть два важных аспекта, которые не отражены в приведенном выше уравнении логистической функции (Taylor and Letham 2017). Во–первых, емкость многих систем непостоянна. Например, число людей, имеющих доступ в Интернет (равно как и количество потенциальных пользователей того или иного онлайн–ресурса) со временем возрастает. Поэтому в пакете prophet постоянная емкость системы \(C\) заменена на динамическую \(C(t)\).

Во–вторых, непостоянной обычно бывает и скорость роста \(k\). Например, выход новой версии продукта может значительно ускорить рост числа его потребителей. В prophet для моделирования такого рода изменений вводится понятие точек излома тренда (разд. 6.4). Предположим, что \(S\) таких точек приходятся на временные отметки \(s_j\), \(j = 1, 2, \dots, S\). Совокупность всех изменений скорости роста \(\delta_j\) можно представить в виде вектора \(\boldsymbol \delta \in \mathbb{R}^S\). Тогда скорость роста в любой точке времени \(t\) будет равна сумме базовой скорости \(k\) и всех изменений, предшествовавших этой точке: \(k + \sum_{j:t > s_j} \delta_j\). Более наглядно это можно представить с помощью такого вектора \(\boldsymbol{a}(t) \in \left\{0, 1\right\}^S\), что \[ a_j(t) = \begin{cases} 1, \; \text{если} \; t \ge s_j \\ 0 \; \text{в остальных случаях} \end{cases} \] Тогда скорость роста в момент времени \(t\) составит \(k + \boldsymbol{a}(t)^\intercal \boldsymbol{\delta}\). При изменении скорости роста необходимо также изменить параметр сдвига \(m\) (см. уравнение выше), чтобы обеспечить гладкий стык сегментов кривой тренда на соответствующей временной отметке. Такая поправка рассчитывается следующим образом: \[\gamma_j = \left(s_j - m -\sum_{l < j}\gamma_l \right) \left(1 - \frac{k + \sum_{l < j} \delta_l}{k + \sum_{l \le j} \delta_l} \right).\] В результате кусочная логистическая функция (piecewise logistic growth model), которая используется в пакете prophet для моделирования тренда с насыщением (saturating growth), принимает вид \[g(t) = \frac{C(t)}{1 + \exp( -(k + \boldsymbol{a}(t)^\intercal \boldsymbol{\delta})(t - (m + \boldsymbol{a}(t)^\intercal \boldsymbol{\gamma})) )}.\] Важным параметром в приведенном уравнении является \(C(t)\) — емкость системы в каждый момент времени. Как задать этот параметр для подгонки модели? Часто у исследователя уже будет хорошее представление о емкости моделируемой системы (например, компании обычно хорошо знают размер рынка, на котором они работают). Если же такого понимания нет, то придется потратить некоторое время на поиск дополнительной информации из сторонних источников (например, прогнозы роста численности населения от Всемирного Банка, тренды в Google–запросах и т.п.).

При неограниченном росте моделируемой системы вместо представленной выше логистической функции в пакете prophet используется кусочно–линейная функция следующего вида (обозначения те же): \[ g(t) = (k + \boldsymbol{a}(t)^\intercal \boldsymbol{\delta})t + (m + \boldsymbol{a}(t)^\intercal \boldsymbol{\gamma}).\] Именно такого рода рост по умолчанию предполагался во всех моделях, которые мы рассматривали в предыдущих разделах этой главы.

6.9.2 Примеры моделей с насыщением тренда

Для начала построим модель, в которой рост зависимой переменной ограничен по некоторому верхнему порогу. Для этого воспользуемся данными по стоимости биткоина за период с января 2016 г. по середину декабря 2017 г., когда наблюдался практически экспоненциальный рост этой переменной (см. рис. 1.3). Предположим, что несмотря на свой экспоненциальный характер роста стоимость биткоина в будущем не могла превысить 11.5 (на логарифмической шкале, что соответствует почти 99000$ (!) на исходной шкале). Для введения этого верхнего порога в модель необходимо добавить новый столбец с (обязательным) именем cap в таблицу с обучающими данными:

Теперь построим модель по этим обучающим данным (обратите внимание использование аргумента growth = "logistic" при вызове функции prophet()), рассчитаем прогноз на следующие 180 дней и изобразим полученный результат (рис. 6.35):

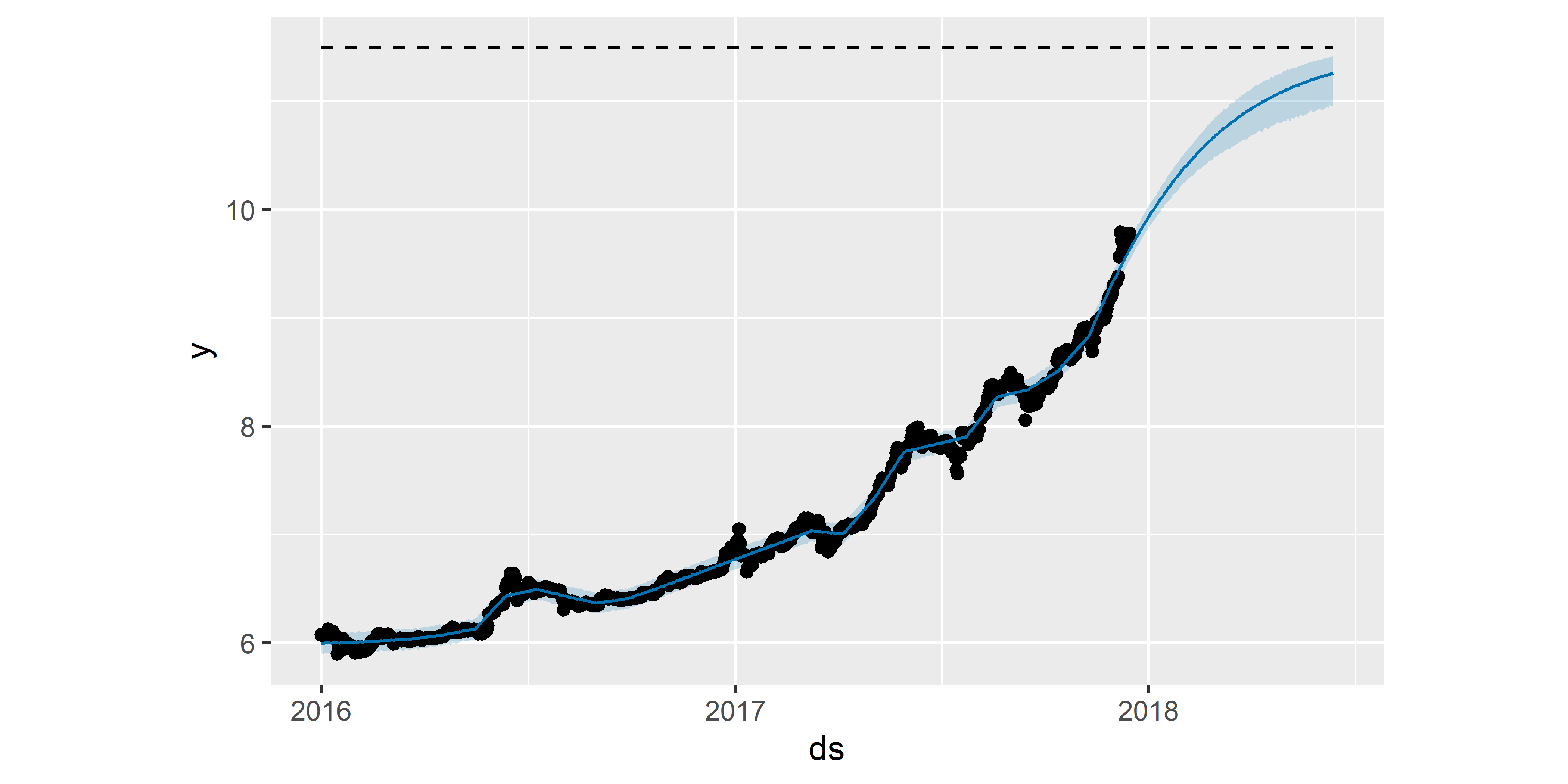
Пример модели с верхним порогом тренда

РИСУНОК 6.35: Пример модели с верхним порогом тренда

Как видим, несмотря на экспоненциальный рост в историческом периоде, предсказанные значения стоимости биткоина постепенно выходят на плато, что обусловлено введенным в модель ограничением на рост.

Многие естественные системы имеют ограничения емкости не только по верхнему, но и нижнему порогу (подобно упомянутой выше численности населения). В prophet имеется возможность учесть это обстоятельство путем добавления еще одного столбца — floor — в таблицы с обучающими данными и данными для расчета прогноза (верхний порог при этом также должен присутствовать в обеих таблицах). Для демонстрации этой возможности воспользуемся данными по стоимости биткоина в 2018 г., когда наблюдался выраженный тренд на ее снижение, и построим модель с верхним ограничением тренда cap = 10 и нижним ограничением floor = 7 (рис. 6.36):

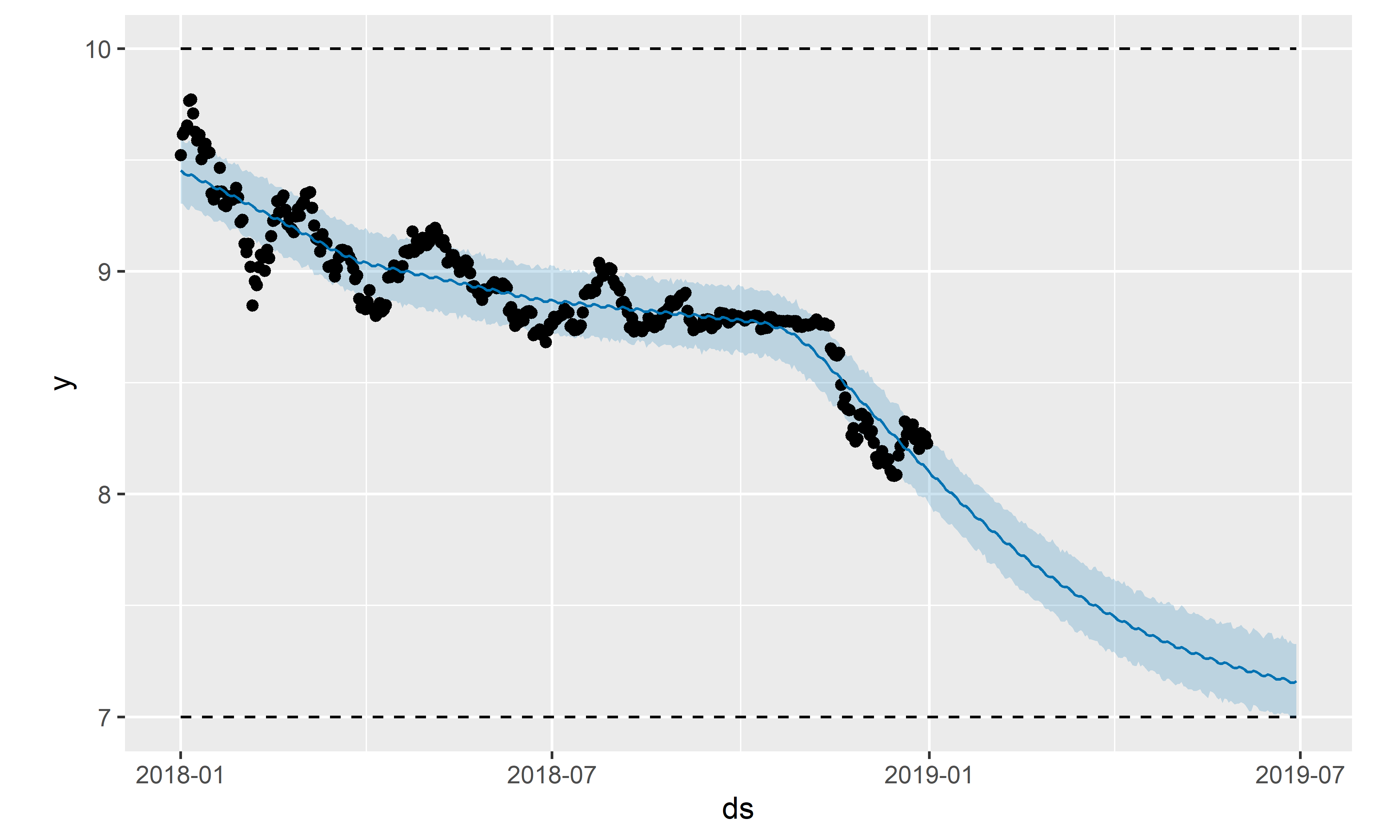
Пример модели с нижним порогом тренда

РИСУНОК 6.36: Пример модели с нижним порогом тренда

В рассмотренных выше примерах предполагалось, что и верхний, и нижний пороги емкости системы постоянны. Если в моделируемой вами системе это не так, то в таблицы с данными для соответствующих дат просто необходимо внести подходящие значения cap и/или floor.