ГЛАВА 11 Кластеризация по исходным данным

Кластеризация по исходным данным подойдет для ситуаций, когда количество анализируемых временных рядов и их длина относительно невелики (иначе могут потребоваться значительные вычислительные ресурсы). Расстояние между двумя временными рядами можно выразить при помощи многих мер, однако, как показано ниже, не все меры одинаково хорошо подходят для этого.

11.1 DTW-расстояние

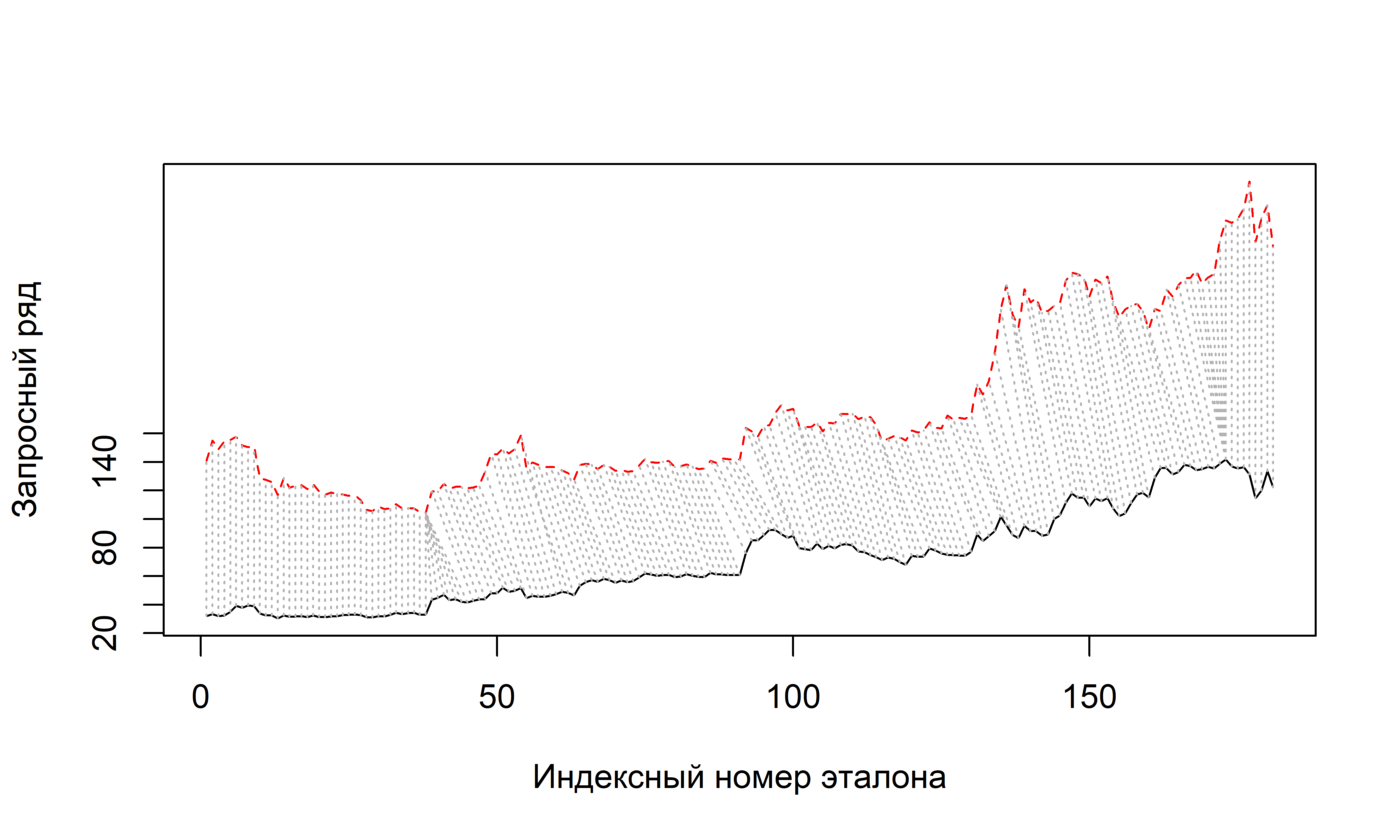
В кластерном анализе и многих других приложениях для описания различий между объектами широко используется евклидово расстояние. В случае с двумя временными рядами $x_i$ и $y_i$, имеющими одинаковый интервал регистрации $n$ наблюдений, оно вычисляется следующим образом (см. также рис. 11.1): \[ d_E = \sqrt{\sum_{i=1}^n (x_{i} - y_{i})^2}.\]

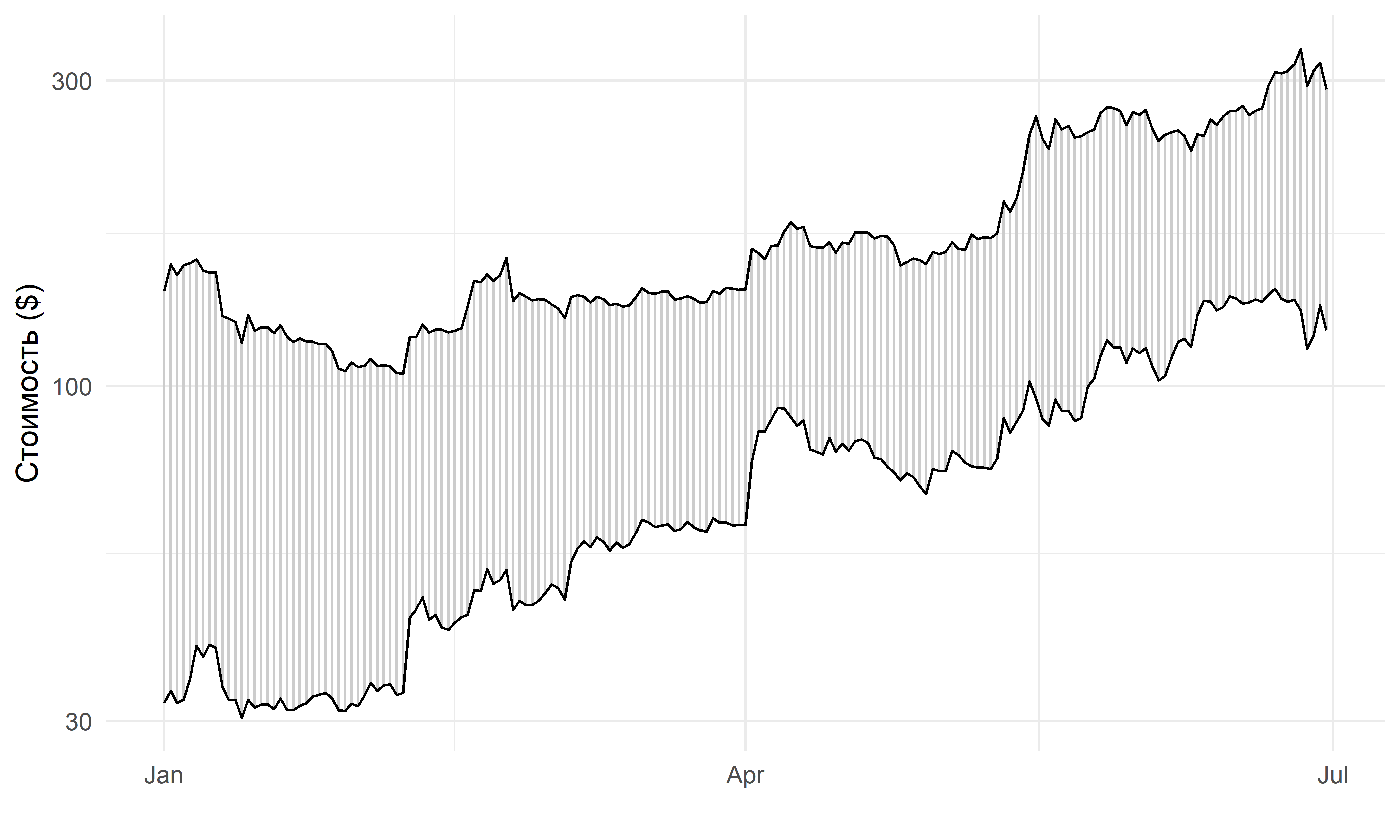
$Евклидово расстояние между двумя временными рядами вычисляется как квадратный корень из суммы квадратов расстояний от каждого $i$–го наблюдения одного ряда до $i$–го наблюдения другого ряда (показаны светло-серыми вертикальными линиями). В качестве примера использованы данные по стоимости криптовалют ethereum (верхний ряд) и litecoin (нижний ряд) за первые 6 месяцев 2019 г.$

РИСУНОК 11.1: Евклидово расстояние между двумя временными рядами вычисляется как квадратный корень из суммы квадратов расстояний от каждого $i$–го наблюдения одного ряда до $i$–го наблюдения другого ряда (показаны светло-серыми вертикальными линиями). В качестве примера использованы данные по стоимости криптовалют ethereum (верхний ряд) и litecoin (нижний ряд) за первые 6 месяцев 2019 г.

К сожалению, евклидово расстояние не всегда является адекватной мерой различий между двумя временными рядами, поскольку оно плохо отражает форму сравниваемых рядов. Для пояснения этого утверждение предположим, что мы создали копию некоторого временного ряда и сдвинули ее по оси времени вправо на несколько шагов. Рассчитав евклидово расстояние между оригиналом и копией, мы бы выяснили, что оно существенно отличается от нуля. Хотя это и ожидаемый результат, в определенной степени он противоречит интуиции — ведь форма обоих рядов идентична! Единственная разница между оригиналом и копией в том, что регистрация наблюдений оригинала началась на несколько временных шагов раньше.

Для решения этой проблемы были разработаны специальные меры расстояния, среди которых особое место занимает т.н. DTW–расстояние, основанное на алгоритме динамической трансформации временной шкалы (Dynamic Time Warping). Впервые эта мера была применена в 1970–х гг. в задаче по распознаванию речи для устранения проблемы, связанной с разной скоростью произнесения одинаковых фраз разными людьми.

Как следует из его названия, алгоритм DTW трансформирует временную шкалу (растягивает или сжимает) с целью достичь оптимального сопоставления (optimal matching), или оптимального выравнивания (optimal alignment), двух последовательностей. Проще говоря, ставится задача расположить два временных ряда относительно друг друга таким образом, чтобы расстояние между ними оказалось минимальным.

Предположим, что мы сравниваем два временных ряда $Q = (q_1, q_2, \dots, q_n)$ и $R = (r_1, r_2, \dots, r_m)$ (эти обозначения происходят от часто используемых в англоязычной литературе терминов “query” — “запрос”, и “reference” — “эталон”). Символами $i = 1 \dots n$ и $j = 1 \dots m$ обозначим соответствующие индексные номера наблюдений из этих двух рядов.

Алгоритм DTW включает две основные стадии. На первой стадии составляют т.н. матрицу локальных потерь $lcm$ (от “Local Cost Matrix”) порядка $n \times m$, каждый элемент $lcm(i, j)$ которой содержит расстояние между парой наблюдений $q_i$ и $r_j$. Обычно используют евклидово или манхэттенское расстояния, хотя можно воспользоваться и другими подходящими случаю мерами.

На второй стадии находят такой путь трансформации (warping path) $\phi = \{(1, 1), \dots, (n, m)\}$ через эту матрицу, который минимизирует суммарное расстояние между рядами $Q$ и $R$. Это расстояние вычисляется следующим образом: \[DTW(Q, R) = \underset{\phi}{min} \left(\sum \frac{m_{\phi} lcm(k)}{M_{\phi}}\right), \forall k \in \phi,\] где $m_{\phi} > 0$ — весовой коэффициент, ассоциированный с каждым элементом $\phi$, а $M_{\phi}$ — константа, нормализующая длину пути (Giorgino 2009).

Поскольку число возможных путей трансформации экспоненциально возрастает с длиной сравниваемых последовательностей, то для нахождения оптимального пути за конечное время вычислений вводят ряд ограничений (constraints). Одно из важных локальных ограничений требует, чтобы путь трансформации был монотонным, т.е. на каждом шаге пути индексам $i$ и $j$ разрешается только возрастать. Это ограничение задается с помощью т.н. шаговых паттернов (step patterns), которые определяют направление разрешенных переходов между ячейками таблицы $lcm$ на каждом шаге. В литературе можно встретить несколько таких шаговых паттернов (Sarda-Espinosa 2019), однако чаще всего используются symmetric1 и symmetric2 (рис. 11.2).

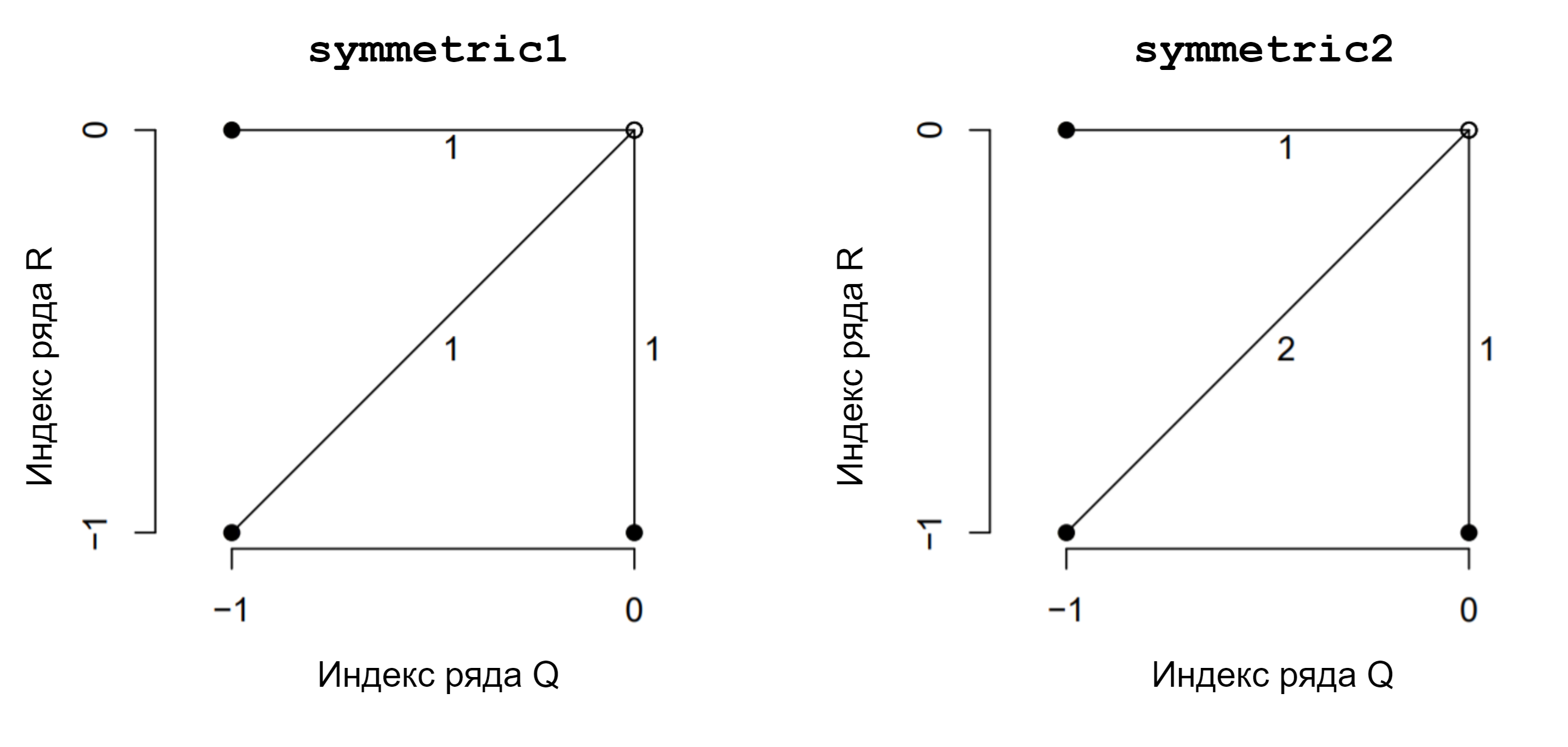
$Наиболее распространенные шаговые паттерны, используемые для нахождения оптимального пути трансформации в алгоритме DTW. Линии, соединяющие точки, соответствуют разрешенными направлениям перехода между ячейками таблицы $lcm$ на каждом шаге пути, а числа рядом с этими линиями — весовым коэффициентам переходов $m_{\phi}$$

РИСУНОК 11.2: Наиболее распространенные шаговые паттерны, используемые для нахождения оптимального пути трансформации в алгоритме DTW. Линии, соединяющие точки, соответствуют разрешенными направлениям перехода между ячейками таблицы $lcm$ на каждом шаге пути, а числа рядом с этими линиями — весовым коэффициентам переходов $m_{\phi}$

Помимо локальных вводятся также и глобальные ограничения. Важнейшим из них является ограничение на ширину окна трансформации (warping window), в пределах которого разрешается прокладывать путь трансформации. Разработано множество разновидностей таких окон, но чаще всего используется т.н. окно Сакэ–Чиба (Sakoe–Chiba window), которое охватывает определенную симметричную область вдоль диагонали матрицы $lcm$ (рис. 11.3).

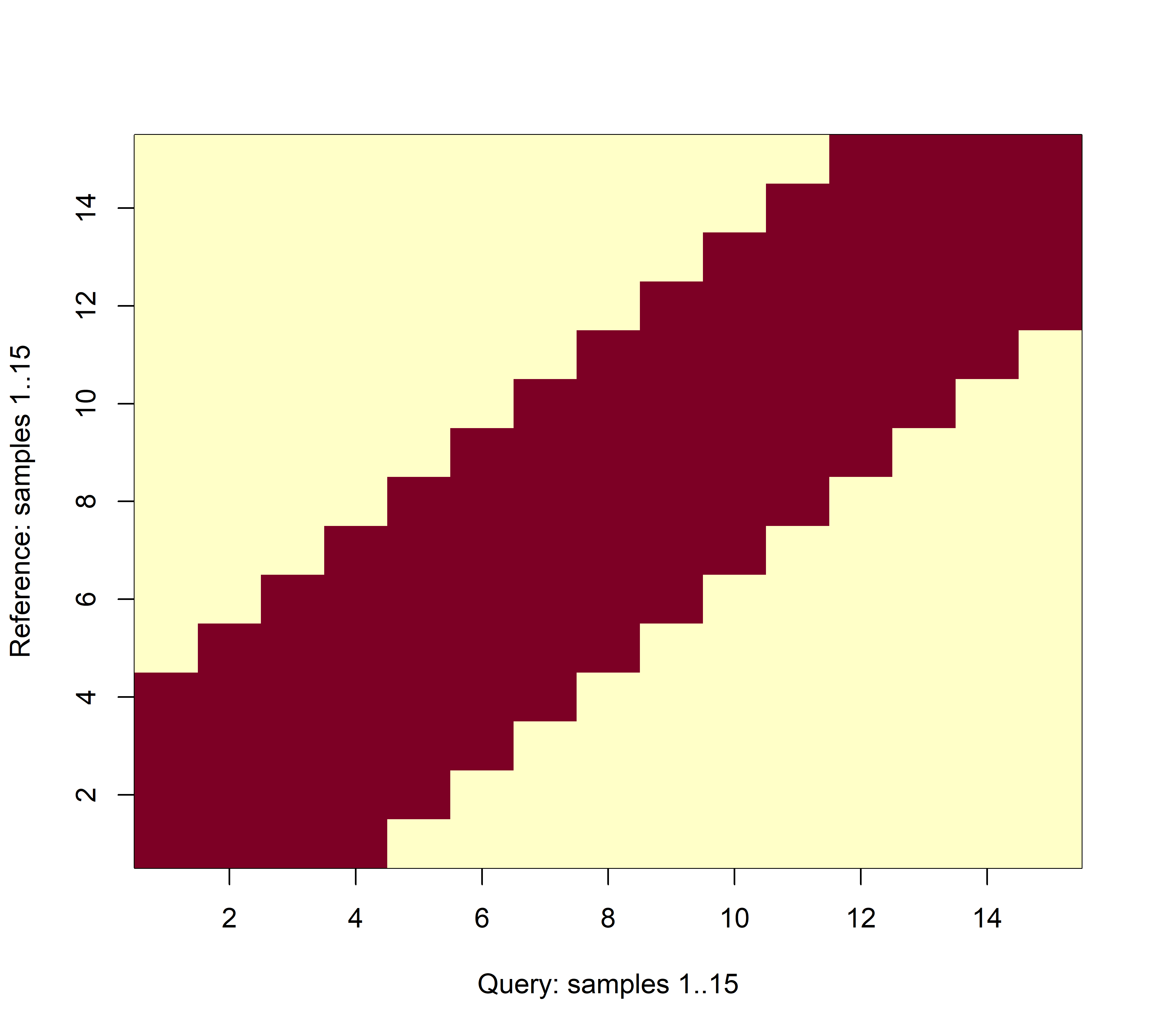
РИСУНОК 11.3: Пример окна Сакэ–Чиба

На рис. 11.4 показан стандартный способ визуализации матрицы локальных потерь $lcm$ (прямоугольник в центре диаграммы), найденного пути трансформации (линия, проходящая примерно по диагонали матрицы) и сравниваемых временных рядов. Индексацию матрицы принято начинать в левом нижнем углу прямоугольника ($lcm(1, 1)$), а заканчивать в правом верхнем ($lcm(m, n)$). Слева от прямоугольника принято изображать “эталон” (reference), т.е. временной ряд, с которым сравнивается изображенный внизу матрицы “запросный” временной ряд (query). Для построения диаграммы был использован пакет dtw (Giorgino 2009).

require(dtw)

alignment <- dtw(
  x = ether_lite_wide$litecoin, # "запрос" 
  y = ether_lite_wide$ethereum, # "эталон"
  step.pattern = symmetric1,    # шаговый паттерн
  window.type = "sakoechiba",   # тип окна трансформации
  window.size = 7,              # размер окна
  keep.internals = TRUE)        # сохранение промежуточных вычислений

plot(alignment, type = "threeway", main = "",
     xlab = "Индексный номер эталона", 
     ylab = "Индексный номер запроса")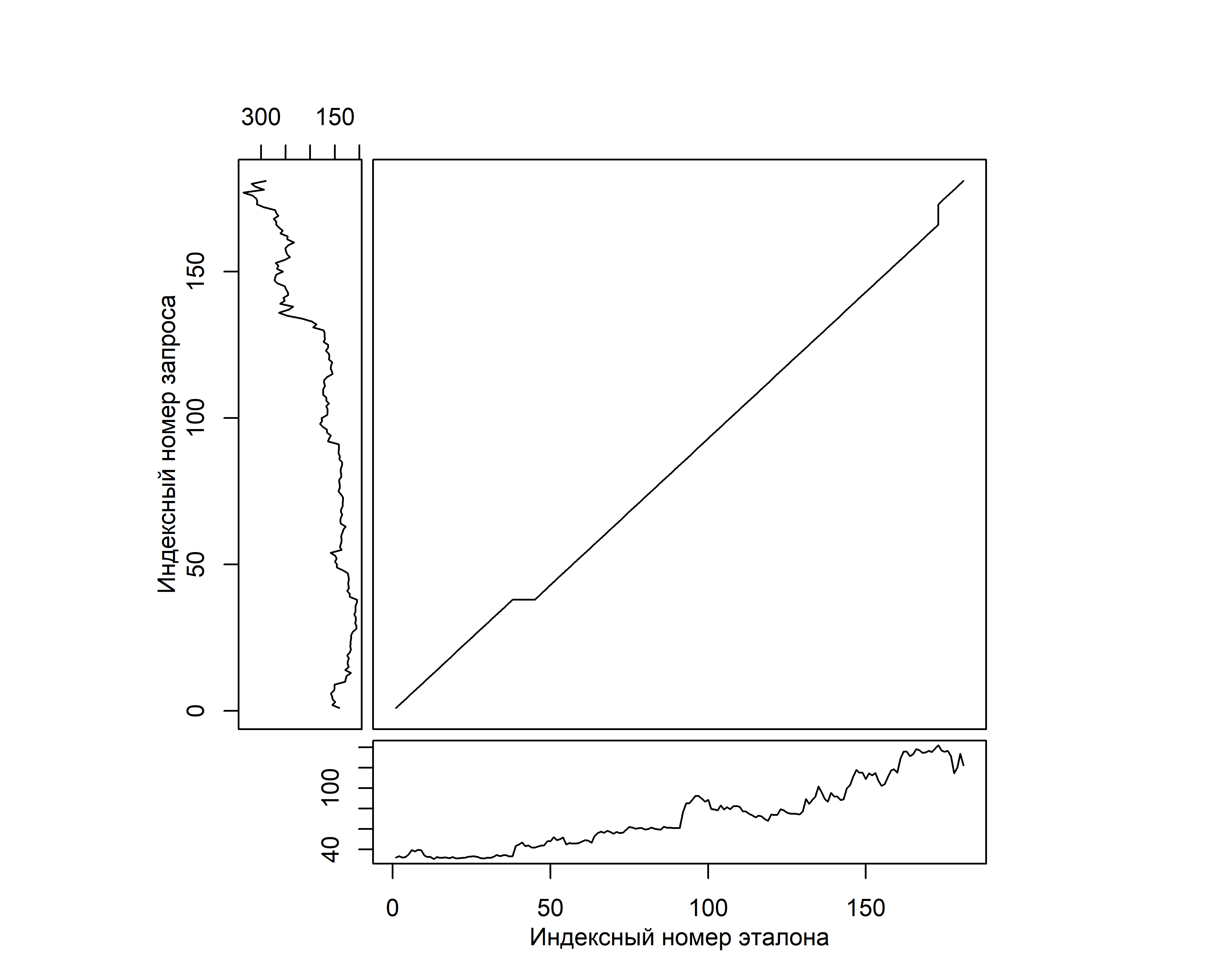

Визуализация оптимального пути DTW–трансформации, найденного при сопоставлении временных рядов стоимости криптовалют ethereum и litecoin

РИСУНОК 11.4: Визуализация оптимального пути DTW–трансформации, найденного при сопоставлении временных рядов стоимости криптовалют ethereum и litecoin

На рис. 11.5 приведен результат оптимального сопоставления временных рядов стоимости криптовалют ethereum и litecoin с помощью алгоритма DTW.

plot(alignment, type = "twoway",
     xlab = "Индексный номер эталона", 
     ylab = "Запросный ряд")

Результат оптимального сопоставления временных рядов стоимости криптовалют ethereum (красная прерывистая линия) и litecoin (черная сплошная линия), полученный с помощью алгоритма DTW (сравните с рис. 11.1). В алгоритме были использованы параметры, приведенные в коде для рис. 11.4

РИСУНОК 11.5: Результат оптимального сопоставления временных рядов стоимости криптовалют ethereum (красная прерывистая линия) и litecoin (черная сплошная линия), полученный с помощью алгоритма DTW (сравните с рис. 11.1). В алгоритме были использованы параметры, приведенные в коде для рис. 11.4

11.2 Пакет `dtwclust`

В R есть несколько пакетов для выполнения кластерного анализа и почти любой из них можно было бы использовать для кластеризации временных рядов. Однако, как это обычно бывает, удобнее иметь один пакет, в котором эффективным образом реализовано большинство подходов, необходимых для решения конкретного круга задач. В случае с временными рядами одним из таких пакетов является dtwclust, который мы и будем использовать в рассматриваемых ниже примерах.

В пакете dtwclust (Sarda-Espinosa (2019)) реализовано большое количество алгоритмов кластеризации временных рядов, включая несколько недавно разработанных методов. За исключением классической иерархической кластеризации, код для всех этих алгоритмов написан специально с целью добиться максимальной скорости вычислений. Вычислительная оптимизация алгоритмов была выполнена исходя из предположения, что в большинстве случаев пользователи будут применять DWT–расстояние в качестве меры различий между временными рядами (отсюда название пакета). Однако имеется возможность использовать и другие меры расстояния, включая пользовательские. Кроме того, с помощью dtwclust можно одновременно сравнить несколько алгоритмов и выбрать оптимальное решение на основе одной или нескольких метрик качества кластеризации.

Главной функцией пакета dtwclust является tsclust(), у которой есть следующие аргументы:

series — список из нескольких временных рядов (не обязательно одинаковой длины), матрица с числовыми значениями или таблица данных. Поскольку все функции dtwclust так или иначе работают со списками временных рядов, то лучше всего на этот аргумент подавать сразу именно такой список. Для формирования списка временных рядов из матриц и таблиц данных можно применить вспомогательную функцию tslist() (при этом предполагается что каждая строка в матрице или таблице данных представляет собой один временной ряд).
type — тип кластеризации: "partitional" (с разбиением), "hierarchical" (иерархическая), "tadpole" (по алгоритму TADPole; Begum et al. 2016) или "fuzzy" (нечеткая кластеризация).
k — запрашиваемое число кластеров. Это может быть также вектор из нескольких целых чисел, если стоит задача проверить качество кластеризации для нескольких решений.
preproc — имя функции, выполняющей предварительную обработку данных. По умолчанию принимает значение NULL. Если аргументу centroid (см. ниже) присвоено значение "shape" (“форма”), то preproc автоматически примет значение zscore, что соответствует функции из пакета dtwclust, которая выполняет стандартизацию данных.
distance — название меры расстояния, зарегистрированное в регистре функции dist() из пакета proxy (см. объяснение ниже). Если type = "tadpole", то этот аргумент будет проигнорирован.
centroid — либо строковое значение с названием метода нахождения центроидов ("mean", "median", "shape" и др.), либо функция, выполняющая нахождение центроидов.
control — список с перечнем управляющих параметров алгоритма, заданного через аргумент type. Для формирования подобных списков служат специальные функции: partitional_control(), hierarchical_control(), fuzzy_control() и tadpole_control() (см. справочный файл, доступный по команде ?"tadpole_control" и примеры ниже).
args — вложенный список параметров, определяющих процесс подготовки данных к анализу (элемент списка с именем preproc), расчета меры расстояния (элемент dist) и центроидов (прототипов) кластеров (элемент cent). Для формирования этого списка служит специальная функция tsclust_args().
seed — значение зерна генератора случайных чисел (позволяет воспроизвести результаты вычислений).
trace — логический аргумент (по умолчанию равен FALSE). При значении TRUE на экран будет выводиться больше служебной информации о ходе вычислений.
error.check — логический аргумент (по умолчанию равен TRUE). Включает или выключает проверку правильности значений перечисленных выше аргументов перед началом вычислений.

Функция tsclust() возвращает объект класса TSClusters, который реализован с использованием S4 — одной из разновидностей классов, применяемых в R для объектно-ориентированного программирования. Отдельные атрибуты объектов класса S4 (“слоты”) можно извлекать с помощью оператора @ (в отличие от обычного $, принятого в S3–объектах). Подробную документацию по классу TSClusters и его методами можно найти в справочных файлах, доступных по командам ?"TSClusters-class" и ?"tsclusters-methods" соответственно.

Пакет dtwclust во многом полагается на другой широко используемый пакет — proxy (автоматически устанавливается и загружается одновременно с dtwclust), в котором реализованы многие меры расстояния. Различная информация о функциях, вычисляющих соответствующие меры расстояния, хранится в специальном объекте–регистре под названием pr_DB. Содержимое регистра можно просмотреть с помощью команды proxy::pr_DB$get_entries() (в целях экономии места пример не приводится). Все зарегистрированные в pr_DB функции автоматически становятся доступными для функции proxy::dist(), которая используется в пакете dtwcust. Это является большим преимуществом дизайна dtwclust, поскольку пользователь получает возможность работать с любой мерой расстояния из pr_DB.

11.3 Пример кластеризации с использованием DTW–расстояния

Рассмотрим особенности работы с пакетом dtwclust на примере иерархической кластеризации временных рядов стоимости 22 криптовалют из таблицы cryptos:

require(dtwclust)

# Преобразование исходных данных в список с 22 элементами,
# содержащими отдельные временные ряды:
cryptos_list <- cryptos %>% 
  mutate(y = log(y)) %>% 
  pivot_wider(., names_from = coin, values_from = y) %>% 
  arrange(ds) %>% 
  dplyr::select(-ds) %>% 
  as.list()

# Кластеризация:
hc_4_ward <- tsclust(
  cryptos_list,
  k = 4,                 # запрашиваемое число кластеров
  type = "hierarchical", # тип кластеризации
  distance = "dtw",      # мера расстояния
  seed = 42,
  control = 
    hierarchical_control(method = "ward.D2"), # метод агломерации
  args = 
    tsclust_args(dist = list(window.size = 7)) # размер окна Сакэ-Чиба
  ) 

hc_4_ward

## hierarchical clustering with 4 clusters
## Using dtw distance
## Using PAM (Hierarchical) centroids
## Using method ward.D2 
## 
## Time required for analysis:
##    user  system elapsed 
##   14.86    1.86   16.73 
## 
## Cluster sizes with average intra-cluster distance:
## 
##   size   av_dist
## 1    5  875.9981
## 2    7 1340.3730
## 3    4 1644.0947
## 4    6  875.1360

Полученный объект hc_4_ward принадлежит к упомянутому выше классу TSClusters и имеет несколько полезных атрибутов. Например, следующим образом можно просмотреть, к какому кластеру принадлежит каждый временной ряд:

hc_4_ward@cluster

##     augur   bitcoin   cardano chainlink      dash    decred  dogecoin       eos 
##         1         2         3         4         2         1         3         1 
##  ethereum      iota  litecoin     maker    monero      nano       neo      qtum 
##         2         4         2         2         2         4         1         1 
##   stellar    tether     tezos      tron       xrp     zcash 
##         3         4         4         3         4         2

Объект hc_4_ward обладает также удобным методом plot(), позволяющим визуализировать полученное кластерное решение. Поскольку мы имеем дело с иерархической кластеризацией, то по умолчанию будет изображена дендрограмма (рис. 11.6):

par(mar = c(0, 4, 2, 2))
plot(hc_4_ward, xlab = "", sub = "", main = "")

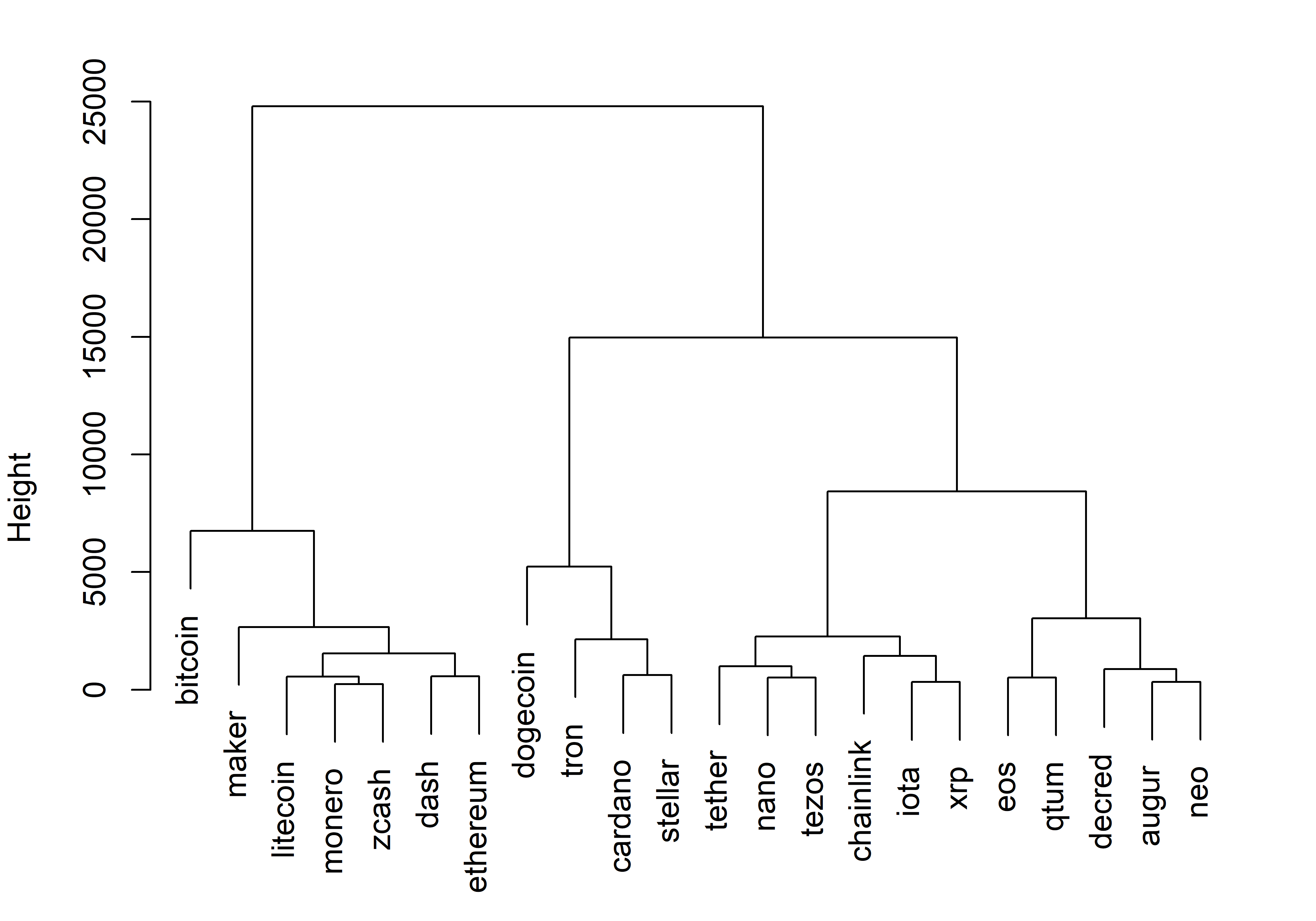
РИСУНОК 11.6: Результат иерархической кластеризации 22 временных рядов, выполненной с использованием DTW–расстояния

Применив функцию plot() с аргументом type = "sc", мы получим изображение анализируемых временных рядов, сгруппированных в соответствии с результатом кластеризации (рис. 11.7). Кроме того, для каждого кластера в виде прерывистой линии будет показан его центроид, или “прототип”. По умолчанию центроиды представляют собой такие временные ряды из исходных данных, которые в среднем ближе всего ко всем остальным рядам из соответствующих кластеров. При необходимости алгоритм расчета центроидов можно изменить с помощью аргумента centroid функции tsclust().

plot(hc_4_ward, type = "sc") # "sc" значит "series and centroids"

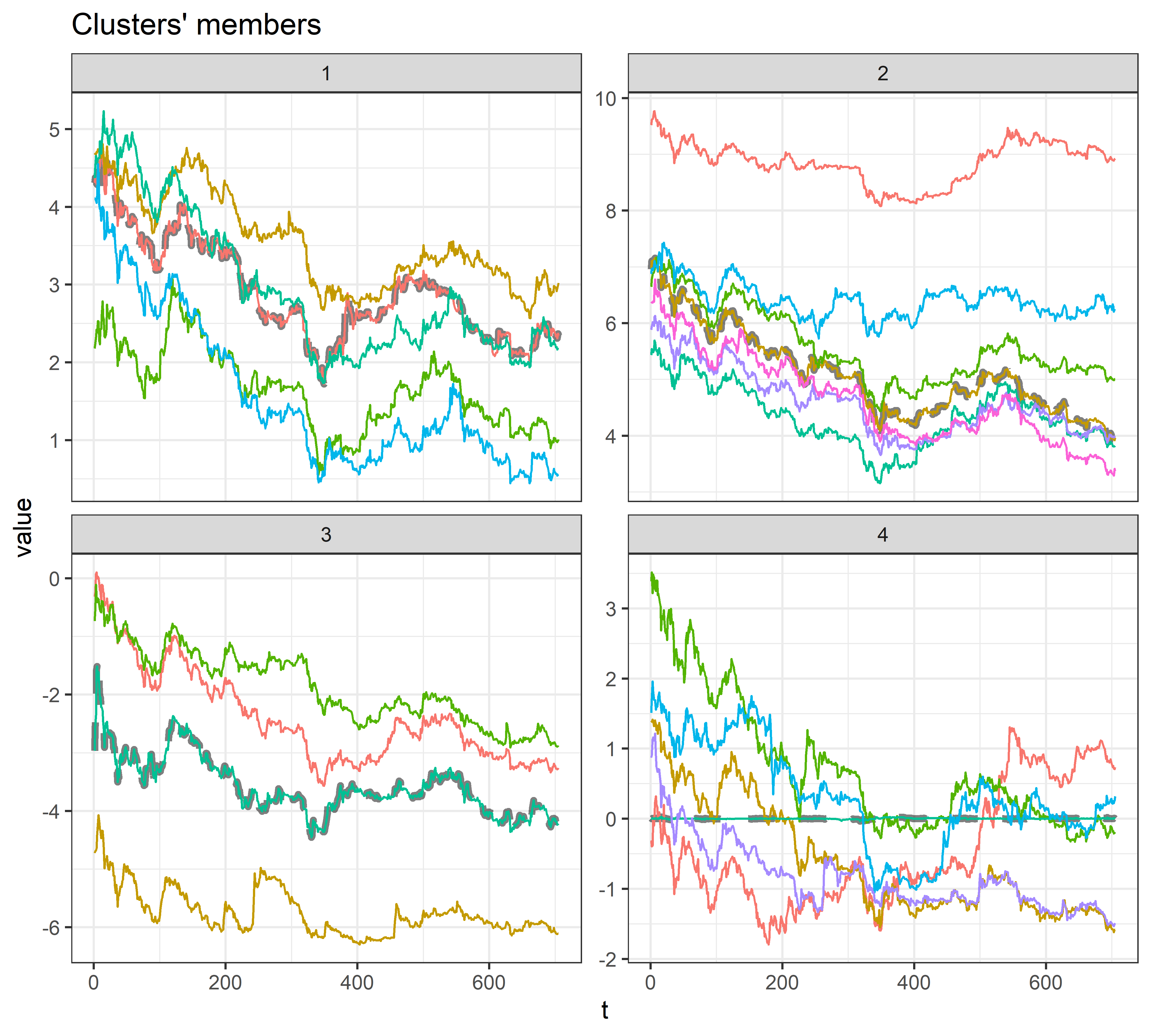
РИСУНОК 11.7: Временные ряды стоимости 22 криптовалют, сгруппированные в соответствии с кластером, к которому они принадлежат

Интересно, что для 4–го кластера в качестве центроида алгоритмом был выбран временной ряд tether, который по сравнению с другими рядами выглядит почти как прямая горизонтальная линия. Однако если “присмотреться поближе”, то можно увидеть, что форма этого ряда далека от горизонтальной линии и отчасти напоминает форму других рядов из кластера 4. Для изображения этого центроида достаточно воспользоваться следующей командой (рис. 11.8):

plot(hc_4_ward, 
     type = "centroids", # включает изображение центроидов
     clus = 4)           # изображает только избранные центроиды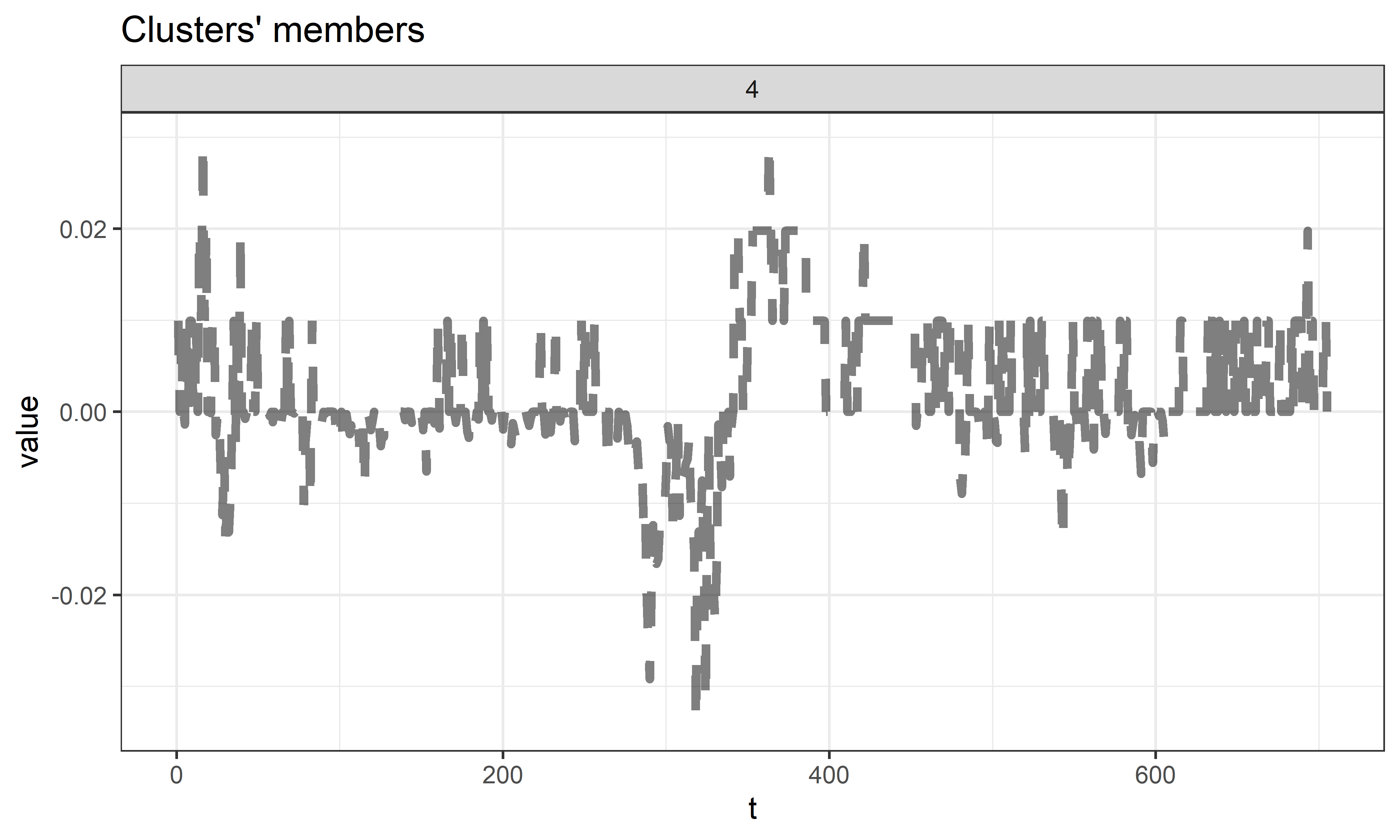

РИСУНОК 11.8: Центроид кластера 4 из объекта hc_4_ward

К сожалению, как видно на рис. 11.7, исходные настройки метода plot() в пакете dtwclust не отличаются особой эстетической привлекательностью: ширина изображающей центроид линии слишком велика, что в сочетании с прерывистостью этой линии затрудняет восприятие графика и понимание свойств временного ряда. К cчастью, метод plot() является лишь оберткой для функций ggplot2, а значит мы можем легко изменить свойства линии (рис. 11.9):

# Аргументы linetype, size и alpha автоматически
# передаются на функцию geom_line() из пакета ggplot2:
plot(hc_4_ward, type = "centroids", clus = 4,
     linetype = 1, size = 0.5, alpha = 1)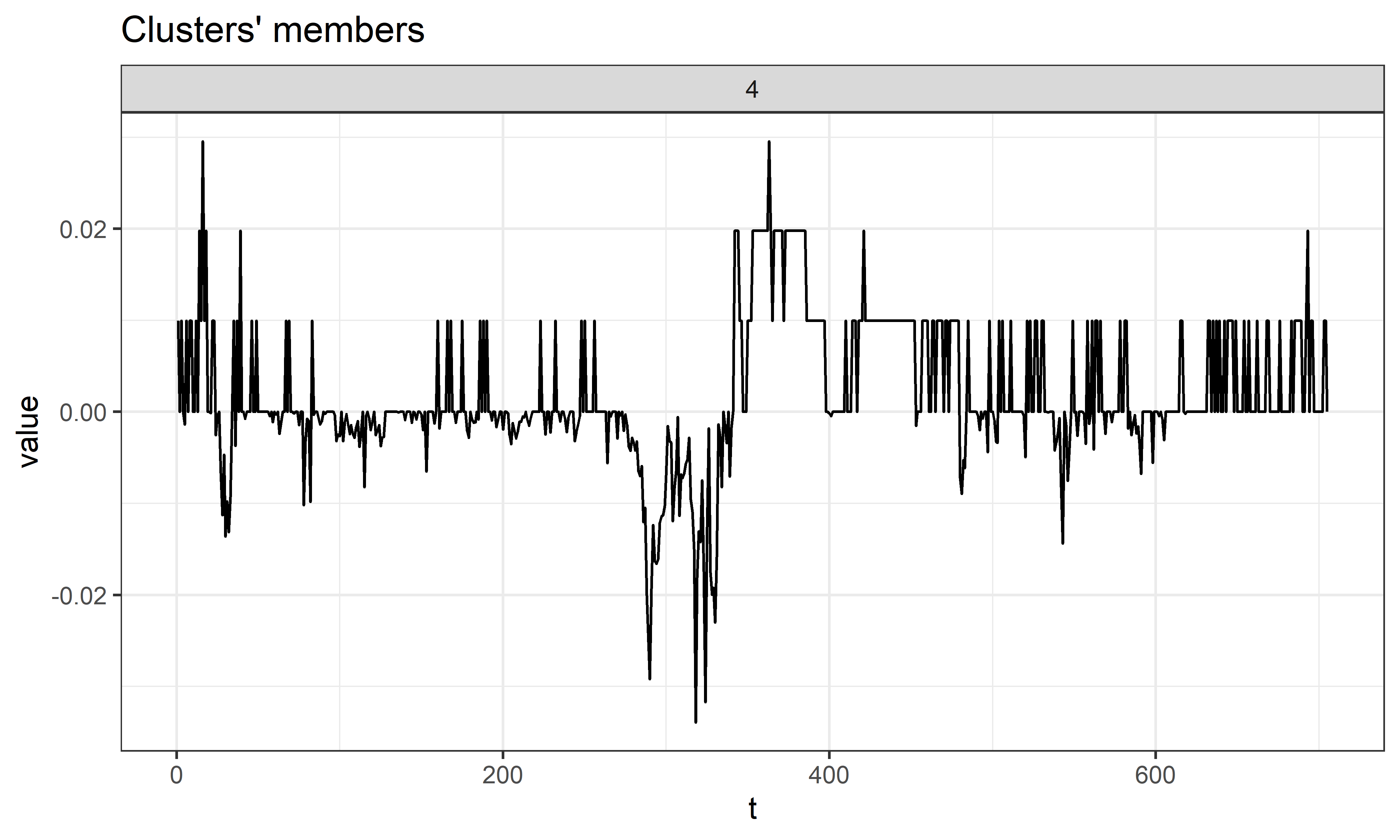

РИСУНОК 11.9: Результат изменения внешнего вида линии, изображающей центроид одного из кластеров

Выполненная нами выше кластеризация была основана на фиксированных параметрах (число выделяемых кластеров, метод кластеризации и др.), выбор которых не был определен какими–то особыми соображениями. К сожалению, как это обычно бывает с кластерным анализом, очень трудно сделать уверенное заключение о “правильности” полученного решения. Тем не менее, как было отмечено в разд. 10, существует ряд метрик, которые пытаются объективно оценить качество кластеризации. В функции cvi() (от “cluster validity indices”, т.е. “индексы валидности кластеров”) реализовано несколько таких метрик, широко используемых при кластеризации временных рядов (подробнее см. справочный файл, доступный по команде ?cvi).

В качестве примера использования cvi() создадим несколько вариантов кластеризации анализируемых нами временных рядов. Тип кластеризации оставим прежним ("hierarchical"), но будем варьировать запрашиваемое число кластеров и методы агломерации:

k <- 3:5
method <- c("ward.D2", "average", "single", 
            "complete", "median", "mcquitty")

Приведенные значения k и method дают 18 комбинаций параметров. Поскольку расчет DTW–расстояния требует значительных вычислительных ресурсов, построение 18 кластерных решений может занять довольно много времени. Один из способов ускорить эти вычисления заключается в использовании существенно оптимизированной (но ограниченной по возможностям) функции dtw_basic() вместо dtw() для расчета DTW–расстояния. Однако мы воспользуемся другим подходом — параллелизацией вычислений. В пакете dtwclust многопоточные параллельные вычисления выполняются с помощью широко используемого для этих целей пакета foreach. Такие вычисления запустятся автоматически при условии существования необходимого “бэкенда”, который можно создать с помощью еще одного популярного пакета — doParallel:

require("doParallel")

# Инициализация локального вычислительного кластера, 
# состоящего из 7 ЦПУ (если нужно, измените это число 
# в соответствии с конфигурацией вашего компьютера)
cl <- makeCluster(7)
registerDoParallel(cl)

hc_par <- tsclust(
  cryptos_list,
  k = k,
  type = "hierarchical",
  distance = "dtw",
  seed = 42,
  control = hierarchical_control(method = method),
  args = tsclust_args(dist = list(window.size = 7)),
  trace = TRUE) # для мониторинга процесса вычислений

## 
## Calculating distance matrix...
## Performing hierarchical clustering...
## Extracting centroids...
## 
##  Elapsed time is 27.94 seconds.

stopCluster(cl) # терминация кластера
registerDoSEQ() # возврат к последовательным вычислениям

Заметьте, что построение всех 18 вариантов кластеризации было выполнено с помощью единственного вызова функции tsclust(). Для этого потребовалось лишь подать векторы с интересующими нас значениями параметров на соответствующие аргументы (k и method). Итогом этих вычислений стал список с 18 элементами, которые содержат отдельные объекты класса TSClusters:

length(hc_par)

## [1] 18

class(hc_par[[1]])

## [1] "HierarchicalTSClusters"
## attr(,"package")
## [1] "dtwclust"

Для нахождения “оптимального” решения можно воспользоваться несколькими индексами “внутренней” валидности кластеров, реализованными в функции cvi(). Поскольку разные индексы могут приводить к разным заключениям о качестве сравниваемых кластеризаций, часто рассчитывают сразу несколько индексов, а затем принимают окончательное заключение на основании простого “большинства голосов”. В приведенном ниже примере мы рассчитаем индекс силуэтов (Silhouette index, "Sil"), индекс Данна (Dunn index, "D") и индекс Калинского–Харабаша (Calinski–Harabasz index, "CH"). Чем больше каждый из этих индексов, тем лучше соответствующее кластерное решение:

lapply(hc_par, cvi, type = c("Sil", "D", "CH")) %>% 
  do.call(rbind, .) %>%
  apply(., MARGIN = 2, FUN = which.max)

## Sil   D  CH 
##   2  15   2

Как видим, два из трех индексов валидности указывают на то, что оптимальным является второе решение (см. также рис. 11.10):

hc_par[[2]]

## hierarchical clustering with 3 clusters
## Using dtw distance
## Using PAM (Hierarchical) centroids
## Using method average 
## 
## Time required for analysis:
##    user  system elapsed 
##    1.18    0.22   27.94 
## 
## Cluster sizes with average intra-cluster distance:
## 
##   size  av_dist
## 1   11 1654.238
## 2    1    0.000
## 3   10 1976.140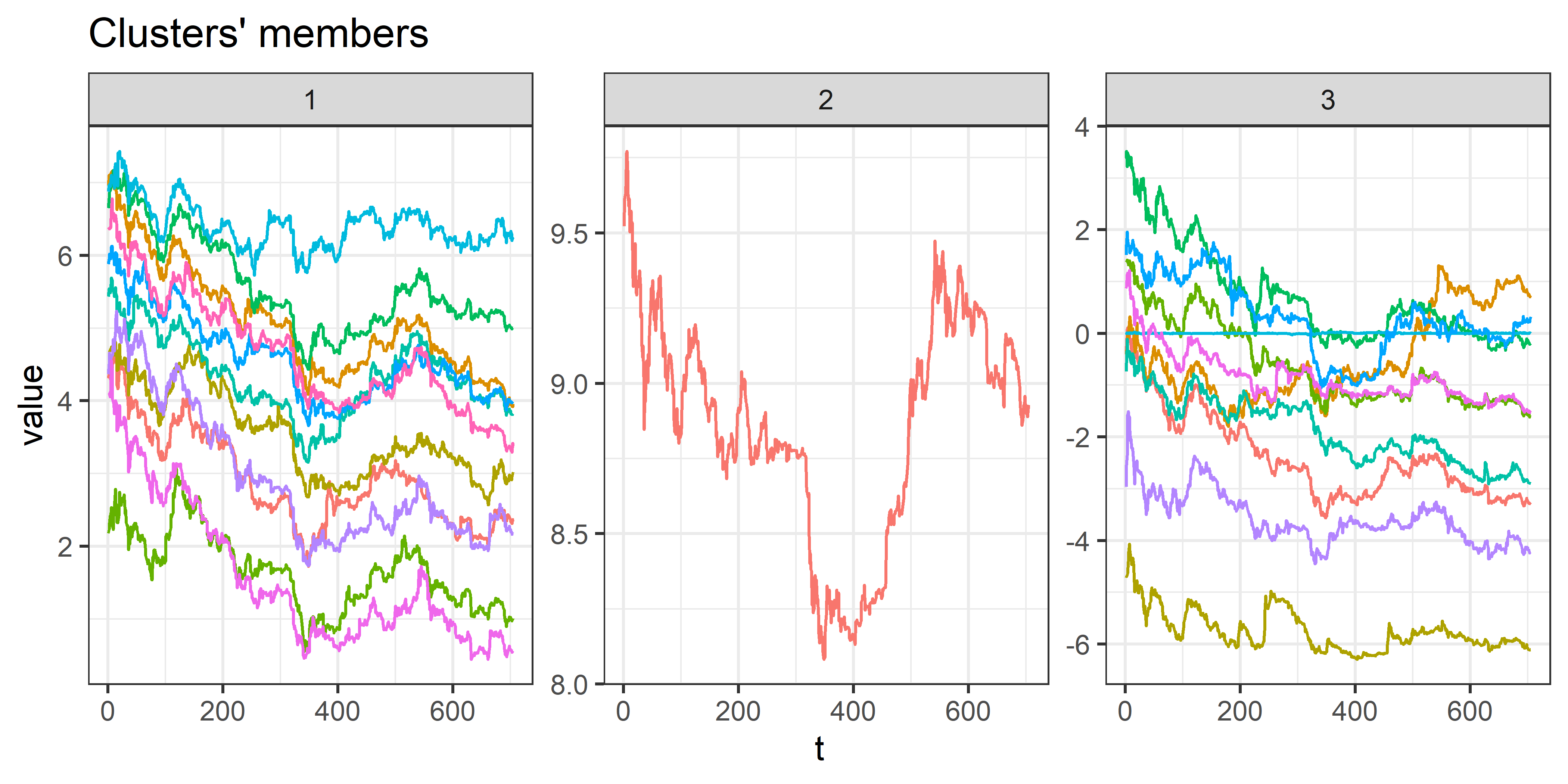

# график временных рядов, без центроидов:
plot(hc_par[[2]], type = "series")

РИСУНОК 11.10: Результат оптимальной иерархической кластеризации временных рядов cryptos, найденной при помощи трех индексов валидности

Рассмотренные выше примеры — это лишь введение в возможности пакета dtwclust. Дополнительную информацию о реализованных в нем методах кластеризации временных рядов можно найти в статье Sarda-Espinosa (2019).

ГЛАВА 11 Кластеризация по исходным данным

11.1 DTW-расстояние

11.2 Пакет dtwclust

11.3 Пример кластеризации с использованием DTW–расстояния

11.2 Пакет `dtwclust`